Question
What is the molar mass of a gas according to the following experimental data?
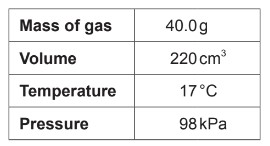
Ideal gas constant = 8.31 \(JK^{-1} mol^{-1}\)
A. \(\frac{40.0 \times 8.31 \times 290}{98 \times 0.220}\)
B. \(\frac{98 \times 0.220}{40.0 \times 8.31 \times 290}\)
C. \(\frac{40.0 \times 8.31 \times 17}{98 \times 0.220}\)
D. \(\frac{98 \times 220}{40.0 \times 8.31 \times 17}\)
▶️Answer/Explanation
Markscheme: A
To find the molar mass of the gas, you can rearrange the ideal gas law equation \(\mathrm{PV}=\mathrm{nRT}\) to solve for the number of moles (\(\mathrm{n}\)) and then use the formula for molar mass (\(\mathrm{M}\)):
\[\mathrm{Molar\ mass} (\mathrm{M}) = \frac{\text{Mass of gas}}{\text{Number of moles}}\]
First, find the number of moles using the ideal gas law:
\[\mathrm{n} = \frac{\mathrm{PV}}{\mathrm{RT}}\]
Now, substitute the given values:
\[\mathrm{n} = \frac{(98 \, \mathrm{kPa}) \times (0.220 \, \mathrm{L})}{(8.31 \, \mathrm{J} \, \mathrm{K}^{-1} \, \mathrm{mol}^{-1}) \times (290 \, \mathrm{K})}\]
Now, substitute the value of \(\mathrm{n}\) into the formula for molar mass:
\[\mathrm{M} = \frac{\text{Mass of gas}}{\text{Number of moles}} = \frac{40.0 \, \mathrm{g}}{\mathrm{n}}\]
so, \[\mathrm{M} =\frac{40.0 \times 8.31 \times 290}{98 \times 0.220}\]
Question
The volume V for a fixed mass of an ideal gas was measured at constant temperature at different pressures p. Which graph shows the correct relationship between pV against p?
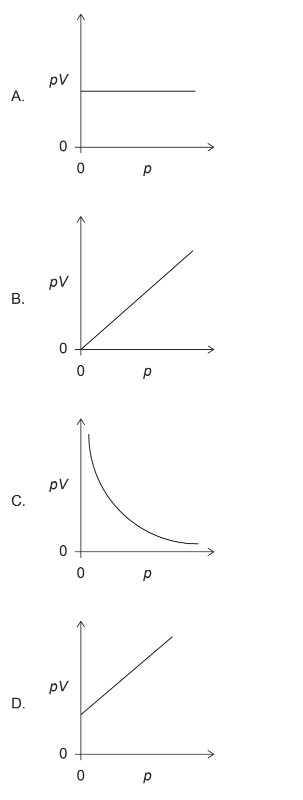
▶️Answer/Explanation
Markscheme: A
For an ideal gas at constant temperature, the relationship between pressure (\(p\)) and volume (\(V\)) is given by Boyle’s Law, which states that the product of pressure and volume is constant:
\[ pV = \text{constant} \]
This implies that \(pV\) is a constant value for an ideal gas at constant temperature.
Therefore, the correct relationship between \(pV\) and \(p\) is a horizontal line on a graph.