Question: [Maximum mark: 4]
Consider the set of six-digit positive integers that can be formed from the digits 0 , 1 , 2, 3, 4 , 5, 6, 7, 8 and 9.
Find the total number of six-digit positive integers that can be formed such that
(a) the digits are distinct;
(b) the digits are distinct and are in increasing order.
▶️Answer/Explanation
Ans:
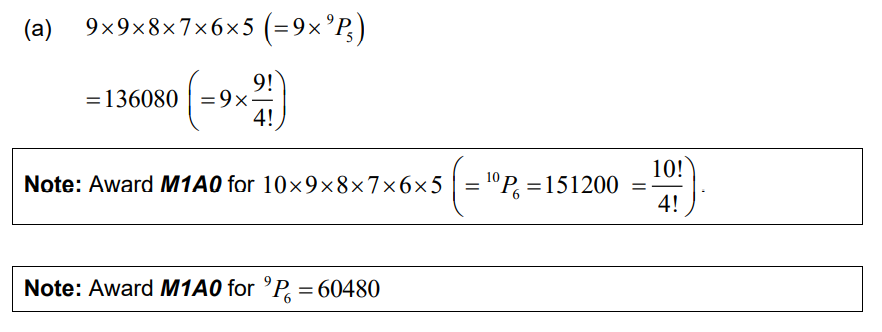
(b) METHOD 1
EITHER
every unordered subset of 6 digits from the set of 9 non-zero digits can be arranged in exactly one way into a 6-digit number with the digits in increasing order.
OR
9C6 (×1)
THEN
= 84
METHOD 2
EITHER
removes 3 digits from the set of 9 non-zero digits and these 6 remaining digits can be arranged in exactly one way into a 6- digit number with the digits in increasing order.
OR
9C3 (×1)
THEN
= 84
Question
Eight runners compete in a race where there are no tied finishes. Andrea and Jack are two of the eight competitors in this race.
Find the total number of possible ways in which the eight runners can finish if Jack finishes.
(a) in the position immediately after Andrea; [2]
(b) in any position after Andrea. [3]
▶️Answer/Explanation
Ans:
(a) $\text{number of ways}=7!=5040$.
(b) $$\begin{eqnarray} \text{number of ways} &=& \binom{7}{1}+\binom{6}{1}+\dots+\binom{2}{1}+\binom{1}{1}\times 6! \nonumber \\ &=& 20160. \end{eqnarray}$$
Question
At a gathering of 12 teachers, seven are male and five are female. A group of five of these teachers go out for a meal together. Determine the possible number of groups in each of the following situations:
There are more males than females in the group. [4]
Two of the teachers, Gary and Gerwyn, refuse to go out for a meal together. [3]
▶️Answer/Explanation
Ans:
(a) identifying two or three possible cases
total number of possible groups is
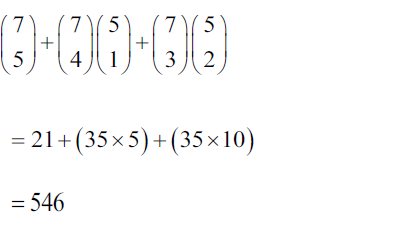
(b) METHOD 1
identifying at least two of the three possible cases- Gary goes, Gerwyn goes or neither goes
total number of possible groups is
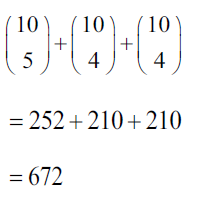
METHOD 2
identifying the overall number of groups and no. of cases where both Gary and Gerwyn go.
total number of possible groups is
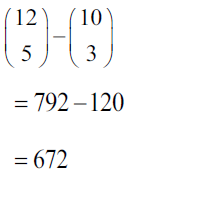
Question
Fifteen boys and ten girls sit in a single line.
In how many ways can they be seated in a single line so that the boys and girls are in two separate groups?[3]
Two boys and three girls are selected to go the theatre. In how many ways can this selection be made?[3]
▶️Answer/Explanation
Markscheme
number of arrangements of boys is \(15!\) and number of arrangements of girls is \(10!\) (A1)
total number of arrangements is \(15! \times 10! \times 2( = 9.49 \times {10^{18}})\) M1A1
Note: If 2 is omitted, award (A1)M1A0.
[3 marks]
number of ways of choosing two boys is \(\left( {\begin{array}{*{20}{c}}
{15} \\
2
\end{array}} \right)\) and the number of ways of choosing three girls is \(\left( {\begin{array}{*{20}{c}}
{10} \\
3
\end{array}} \right)\) (A1)
number of ways of choosing two boys and three girls is \(\left( {\begin{array}{*{20}{c}}
{15} \\
2
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
{10} \\
3
\end{array}} \right) = 12600\) M1A1
[3 marks]