Question
Consider the complex numbers z = 2 \((cos\frac{\pi }{5}+isin\frac{\pi }{5})\) and w = 8 \((cos\frac{2k\pi }{5}- isin\frac{2k\pi }{5})\) where \(k\in \mathbb{Z}^+\)
Find the modulus of \(zw\). [1]
Find the argument of \(zw\) in terms of \(k\) . [2]
Suppose that \(zw\in \mathbb{Z}\) .
(i) Find the minimum value of \(k\) .
(ii) For the value of k found in part (i), find the value of \(zw\) . [4]
▶️Answer/Explanation
Ans:
(a) (|zw|=)16
(b)
attempt to find arg (z) +arg (w)
arg (zw)=arg (z)+arg (w)
= \(\frac{\pi}{5}-\frac{2k\pi}{5}=\frac{(1-2k)\pi}{5}\)
(c)
(i)
zw \(\varepsilon Z\Leftrightarrow arg (zw)\) is a multiple of \(\pi\)
\(\Leftrightarrow 1-2k\) is a multiple of 5
k =3
(ii) zw =16 \(cos(-\pi)+isin(-\pi)\)- 16
Question
Consider the complex number \(z = \frac{{2 + 7{\text{i}}}}{{6 + 2{\text{i}}}}\).
a.Express \(z\) in the form \(a + {\text{i}}b\), where \(a,\,b \in \mathbb{Q}\).[2]
b.Find the exact value of the modulus of \(z\).[2]
c.Find the argument of \(z\), giving your answer to 4 decimal places.[2]
▶️Answer/Explanation
Markscheme
\(z = \frac{{\left( {2 + 7{\text{i}}} \right)}}{{\left( {6 + 2{\text{i}}} \right)}} \times \frac{{\left( {6 – 2{\text{i}}} \right)}}{{\left( {6 – 2{\text{i}}} \right)}}\) (M1)
\( = \frac{{26 + 38{\text{i}}}}{{40}} = \left( {\frac{{13 + 19{\text{i}}}}{{20}} = 0.65 + 0.95{\text{i}}} \right)\) A1
[2 marks]
attempt to use \(\left| z \right| = \sqrt {{a^2} + {b^2}} \) (M1)
\(\left| z \right| = \sqrt {\frac{{53}}{{40}}} \left( { = \frac{{\sqrt {530} }}{{20}}} \right)\) or equivalent A1
Note: A1 is only awarded for the correct exact value.
[2 marks]
EITHER
arg \(z\) = arg(2 + 7i) − arg(6 + 2i) (M1)
OR
arg \(z\) = arctan\(\left( {\frac{{19}}{{13}}} \right)\) (M1)
THEN
arg \(z\) = 0.9707 (radians) (= 55.6197 degrees) A1
Note: Only award the last A1 if 4 decimal places are given.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
(a) Solve the equation \({z^3} = – 2 + 2{\text{i}}\), giving your answers in modulus-argument form.
(b) Hence show that one of the solutions is 1 + i when written in Cartesian form.
▶️Answer/Explanation
Markscheme
(a) \({z^3} = 2\sqrt 2 {{\text{e}}^{\frac{{3\pi {\text{i}}}}{4}}}\) (M1)(A1)
\({z_1} = \sqrt 2 {{\text{e}}^{\frac{{\pi {\text{i}}}}{4}}}\) A1
adding or subtracting \(\frac{{2\pi {\text{i}}}}{3}\) M1
\({z_2} = \sqrt 2 {{\text{e}}^{\frac{{\pi {\text{i}}}}{4} + \frac{{2\pi {\text{i}}}}{3}}} = \sqrt 2 {{\text{e}}^{\frac{{11\pi {\text{i}}}}{{12}}}}\) A1
\({z_3} = \sqrt 2 {{\text{e}}^{\frac{{\pi {\text{i}}}}{4} – \frac{{2\pi {\text{i}}}}{3}}} = \sqrt 2 {{\text{e}}^{ – \frac{{5\pi {\text{i}}}}{{12}}}}\) A1
Notes: Accept equivalent solutions e.g. \({z_3} = \sqrt 2 {{\text{e}}^{\frac{{19\pi {\text{i}}}}{{12}}}}\)
Award marks as appropriate for solving \({(a + b{\text{i}})^3} = – 2 + 2{\text{i}}\).
Accept answers in degrees.
(b) \(\sqrt 2 {{\text{e}}^{\frac{{\pi {\text{i}}}}{4}}}{\text{ }}\left( { = \sqrt 2 \left( {\frac{1}{{\sqrt 2 }} + \frac{{\text{i}}}{{\sqrt 2 }}} \right)} \right)\) A1
= 1 + i AG
Note: Accept geometrical reasoning.
[7 marks]
Examiners report
Many students incorrectly found the argument of \({z^3}\) to be \(\arctan \left( {\frac{2}{{ – 2}}} \right) = – \frac{\pi }{4}\). Of those students correctly finding one solution, many were unable to use symmetry around the origin, to find the other two. In part (b) many students found the cube of 1 + i which could not be awarded marks as it was not “hence”.
Question
The complex numbers \(u\) and \(v\) are represented by point A and point B respectively on an Argand diagram.
Point A is rotated through \(\frac{\pi }{2}\) in the anticlockwise direction about the origin O to become point \({\text{A}}’\). Point B is rotated through \(\frac{\pi }{2}\) in the clockwise direction about O to become point \({\text{B}}’\).
a.Consider \(z = r(\cos \theta + {\text{i}}\sin \theta ),{\text{ }}z \in \mathbb{C}\).
Use mathematical induction to prove that \({z^n} = {r^n}(\cos n\theta + {\text{i}}\sin n\theta ),{\text{ }}n \in {\mathbb{Z}^ + }\).[7]
(i) express \(u\) and \(v\) in modulus-argument form;
(ii) hence find \({u^3}{v^4}\).[4]
c.Plot point A and point B on the Argand diagram.[1]
d.Find the area of triangle O\({\text{A}}’\)\({\text{B}}’\).[3]
e.Given that \(u\) and \(v\) are roots of the equation \({z^4} + b{z^3} + c{z^2} + dz + e = 0\), where \(b,{\text{ }}c,{\text{ }}d,{\text{ }}e \in \mathbb{R}\),
find the values of \(b,{\text{ }}c,{\text{ }}d\) and \(e\).[5]
▶️Answer/Explanation
Markscheme
let \({\text{P}}(n)\) be the proposition \({z^n} = {r^n}(\cos n\theta + {\rm{i}}\sin n\theta ),n \in {¢^ + }\)
let \(n = 1 \Rightarrow \)
\({\text{LHS}} = r(\cos \theta + {\text{i}}\sin \theta )\)
\({\text{RHS}} = r(\cos \theta + {\text{i}}\sin \theta ),{\text{ }}\therefore {\text{P}}(1)\) is true R1
assume true for \(n = k \Rightarrow {r^k}{(\cos \theta + {\text{i}}\sin \theta )^k} = {r^k}\left( {\cos (k\theta ) + {\text{i}}\sin (k\theta )} \right)\) M1
Note: Only award the M1 if truth is assumed.
now show \(n = k\) true implies \(n = k + 1\) also true
\({r^{k + 1}}{(\cos \theta + {\text{i}}\sin \theta )^{k + 1}} = {r^{k + 1}}{(\cos \theta + {\text{i}}\sin \theta )^k}(\cos \theta + {\text{i}}\sin \theta )\) M1
\( = {r^{k + 1}}\left( {\cos (k\theta ) + {\text{i}}\sin (k\theta )} \right)(\cos \theta + {\text{i}}\sin \theta )\)
\( = {r^{k + 1}}\left( {\cos (k\theta )\cos \theta – \sin (k\theta )\sin \theta + {\text{i}}\left( {\sin (k\theta )\cos \theta + \cos (k\theta )\sin \theta } \right)} \right)\) A1
\( = {r^{k + 1}}\left( {\cos (k\theta + \theta ) + {\text{i}}\sin (k\theta + \theta )} \right)\) A1
\( = {r^{k + 1}}\left( {\cos (k + 1)\theta + {\text{i}}\sin (k + 1)\theta } \right) \Rightarrow n = k + 1\) is true A1
\({\text{P}}(k)\) true implies \({\text{P}}(k + 1)\) true and \({\text{P}}(1)\) is true, therefore by mathematical induction statement is true for \(n \geqslant 1\) R1
Note: Only award the final R1 if the first 4 marks have been awarded.
[7 marks]
(i) \(u = 2{\text{cis}}\left( {\frac{\pi }{3}} \right)\) A1
\(v = \sqrt 2 {\text{cis}}\left( { – \frac{\pi }{4}} \right)\) A1
Notes: Accept 3 sf answers only. Accept equivalent forms.
Accept \(2{e^{\frac{\pi }{3}i}}\) and \(\sqrt 2 {e^{ – \frac{\pi }{4}i}}\).
(ii) \({u^3} = {2^3}{\text{cis}}(\pi ) = – 8\)
\({v^4} = 4{\text{cis}}( – \pi ) = – 4\) (M1)
\({u^3}{v^4} = 32\) A1
Notes: Award (M1) for an attempt to find \({u^3}\) and \({v^4}\).
Accept equivalent forms.
[4 marks]
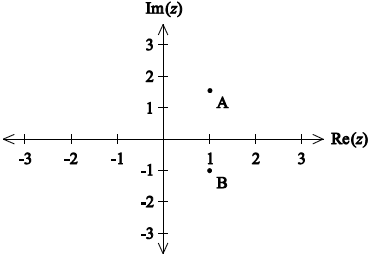 A1
A1
Note: Award A1 if A or \({\text{1 + }}\sqrt 3 i\) and B or \(1 – i\) are in their correct quadrants, are aligned vertically and it is clear that \(\left| u \right| > \left| v \right|\).
[1 mark]
Area \( = \frac{1}{2} \times 2 \times \sqrt 2 \times \sin \left( {\frac{{5\pi }}{{12}}} \right)\) M1A1
\( = 1.37{\text{ }}\left( { = \frac{{\sqrt 2 }}{4}\left( {\sqrt 6 + \sqrt 2 } \right)} \right)\) A1
Notes: Award M1A0A0 for using \(\frac{{7\pi }}{{12}}\).
[3 marks]
\((z – 1 + {\text{i}})(z – 1 – {\text{i}}) = {z^2} – 2z + 2\) M1A1
Note: Award M1 for recognition that a complex conjugate is also a root.
\(\left( {z – 1 – \sqrt 3 {\text{i}}} \right)\left( {z – 1 + \sqrt 3 {\text{i}}} \right) = {z^2} – 2z + 4\) A1
\(\left( {{z^2} – 2z + 2} \right)\left( {{z^2} – 2z + 4} \right) = {z^4} – 4{z^3} + 10{z^2} – 12z + 8\) M1A1
Note: Award M1 for an attempt to expand two quadratics.
[5 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]