Question
Sketch on the same axes the curve \(y = \left| {\frac{7}{{x – 4}}} \right|\) and the line \(y = x + 2\), clearly indicating any axes intercepts and any asymptotes.[3]
Find the exact solutions to the equation \(x + 2 = \left| {\frac{7}{{x – 4}}} \right|\).[5]
Answer/Explanation
Markscheme
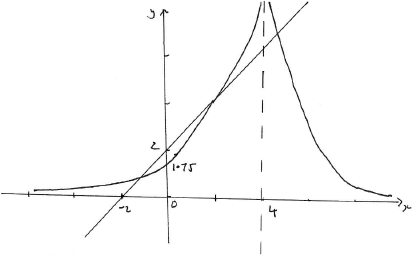
A1 for vertical asymptote and for the \(y\)-intercept \(\frac{7}{4}\)
A1 for general shape of \(y = \left| {\frac{7}{{x – 4}}} \right|\) including the \(x\)-axis as asymptote
A1 for straight line with \(y\)-intercept 2 and \(x\)-intercept of \( – 2\) A1A1A1
[3 marks]
METHOD 1
for \(x > 4\)
\((x + 2)(x – 4) = 7\) (M1)
\({x^2} – 2x – 8 = 7 \Rightarrow {x^2} – 2x – 15 = 0\)
\((x – 5)(x + 3) = 0\)
\(({\text{as }}x > 4{\text{ then}}){\text{ }}x = 5\) A1
Note: Award A0 if \(x = – 3\) is also given as a solution.
for \(x < 4\)
\((x + 2)(x – 4) = – 7\) M1
\( \Rightarrow {x^2} – 2x – 1 = 0\)
\(x = \frac{{2 \pm \sqrt {4 + 4} }}{2} = 1 \pm \sqrt 2 \) (M1)A1
Note: Second M1 is dependent on first M1.
[5 marks]
METHOD 2
\({(x + 2)^2} = \frac{{49}}{{{{(x – 4)}^2}}}\) M1
\({x^4} – 4{x^3} – 12{x^2} + 32x + 15 = 0\) A1
\((x + 3)(x – 5)({x^2} – 2x – 1) = 0\)
\(x = 5\) A1
Note: Award A0 if \(x = – 3\) is also given as a solution.
\(x = \frac{{2 \pm \sqrt {4 + 4} }}{2} = 1 \pm \sqrt 2 \) (M1)A1
[5 marks]
Question
A rational function is defined by \(f(x) = a + \frac{b}{{x – c}}\) where the parameters \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\) and \(x \in \mathbb{R}\backslash \{ c\} \). The following diagram represents the graph of \(y = f(x)\).
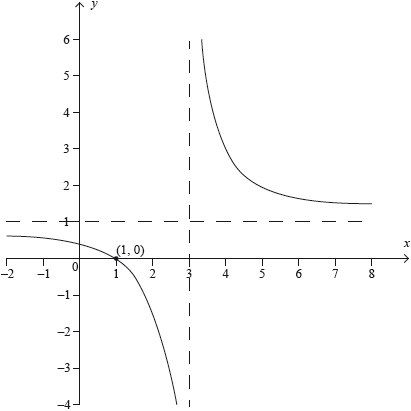
Using the information on the graph,
state the value of \(a\) and the value of \(c\);[2]
find the value of \(b\).[2]
Answer/Explanation
Markscheme
\(a = 1\) A1
\(c = 3\) A1
[2 marks]
use the coordinates of \((1,{\text{ }}0)\) on the graph M1
\(f(1) = 0 \Rightarrow 1 + \frac{b}{{1 – 3}} = 0 \Rightarrow b = 2\) A1
[2 marks]
Question
Sketch the graphs of \(y = \frac{x}{2} + 1\) and \(y = \left| {x – 2} \right|\) on the following axes.
 [3]
[3]
Solve the equation \(\frac{x}{2} + 1 = \left| {x – 2} \right|\).[4]
Answer/Explanation
Markscheme
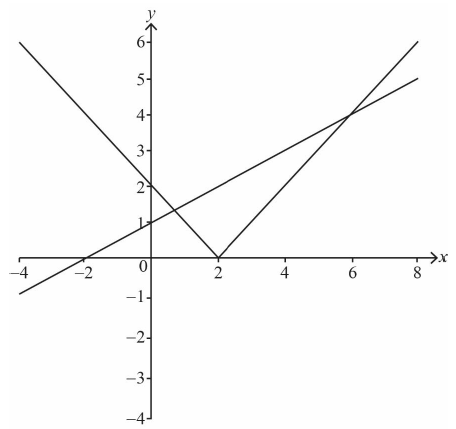
straight line graph with correct axis intercepts A1
modulus graph: V shape in upper half plane A1
modulus graph having correct vertex and y-intercept A1
[3 marks]
METHOD 1
attempt to solve \(\frac{x}{2} + 1 = x – 2\) (M1)
\(x = 6\) A1
Note: Accept \(x = 6\) using the graph.
attempt to solve (algebraically) \(\frac{x}{2} + 1 = 2 – x\) M1
\(x = \frac{2}{3}\) A1
[4 marks]
METHOD 2
\({\left( {\frac{x}{2} + 1} \right)^2} = {\left( {x – 2} \right)^2}\) M1
\(\frac{{{x^2}}}{4} + x + 1 = {x^2} – 4x + 4\)
\(0 = \frac{{3{x^2}}}{4} – 5x + 3\)
\(3{x^2} – 20x + 12 = 0\)
attempt to factorise (or equivalent) M1
\(\left( {3x – 2} \right)\left( {x – 6} \right) = 0\)
\(x = \frac{2}{3}\) A1
\(x = 6\) A1
[4 marks]