Question
Let α,β,γ be the roots of the cubic function
f(x) = x3 – 5x2 – 7x + 3
Find, without estimating the roots α,β,γ
(a) α + β + γ, αβγ and αβ + βγ + γα
(b) α2 + β2 + γ2
(c) (αβ)2 + (βγ)2 + (γα)2
(d) a cubic polynomial which has roots α2, β2, γ2.
▶️Answer/Explanation
Ans
(a) α + β + γ = 5, αβγ = -3 and αβ + βγ + γα = -7
(b) We use (α + β + γ)2 = α2 + β2 + γ2 + 2αβ + 2βγ + 2γα
\(\Rightarrow \) α2 + β2 + γ2 = (α + β + γ)2 – 2(αβ + βγ + γα)
Thus α2 + β2 + γ2 = 25 + 2(-7) = 39
(c) We use (αβ + βγ + γα)2 = (αβ)2 + (βγ)2 + (γα)2 + 2αβ2γ + 2αβγ2 + 2α2βγ
\(\Rightarrow\) (αβ)2 + (βγ)2 + (γα)2 = (αβ + βγ + γα)2 – 2αβγ(α + β + γ)
Thus (αβ)2 + (βγ)2 + (γα)2 = (-7)2 – 2(-3)(5) = 79
(d) Since α2 + β2 + γ2 = 39, α2β2γ2 = (αβγ)2 = 9, α2β2 + β2γ2 + γ2α2 = 79 the polynomial is x3 – 39x2 + 79x – 9 (or any multiple).
Question
Let α, β be the roots of the quadratic f(x) = 5x2 – 2x – 4
Without estimating the roots α, β, find
(a) α + β and αβ
(b) α2 + β2 and α3 + β3
(c) a quadratic with integer coefficients which has roots α2, β2.
(d) a quadratic with integer coefficients which has roots \(\frac{1}{\alpha },\frac{1}{\beta }\).
Remember: in a cubic function ax3 + bx2 + cx + d with roots r1, r2, r3
▶️Answer/Explanation
Ans
(a)
α + β = \(\frac{2}{5}\), αβ = \(-\frac{4}{5}\)
(b) We use (α + β)2 = α2 + 2αβ + β2
\(\Rightarrow \alpha ^{2}+\beta ^2=(\alpha +\beta )^2-\alpha \beta \)
Thus \(\alpha ^2+\beta ^2=\frac{4}{25}+\frac{8}{5}=\frac{44}{25}\)
We use \((\alpha +\beta )^3 = \alpha ^3 + 3\alpha ^2\beta +3\alpha \beta^2+\beta ^3\)
\(\Rightarrow \alpha ^3+\beta ^3=(\alpha +\beta )^3-3\alpha \beta (\alpha +\beta )\)
Thus \(\alpha ^3+\beta ^3=\frac{8}{125}+3.\frac{4}{5}.\frac{2}{5}=\frac{128}{125}\)
(c) Since \(\alpha ^2+\beta ^2=\frac{44}{25}\) and \(\alpha ^2\beta ^2=\frac{16}{25}\)
the polynomial is 25x2 – 44x + 16
(d) Since \(\frac{1}{\alpha }+\frac{1}{\beta }=\frac{\alpha +\beta }{\alpha \beta }=-\frac {2}{4}\) and \(\frac{1}{\alpha }.\frac{1}{\beta }=-\frac{5}{4}\)
the polynomial is 4x2 + 2x – 5 (or any multiple).
\(r_1+r_2+r_3=-\frac{b}{a}\) \(r_1r_2r_3=-\frac{d}{a}\) and \(r_1r_2+r_2r_3+r_3r_1=\frac{c}{a}\)
Question
Let \(f(x) = {x^4} + 0.2{x^3} – 5.8{x^2} – x + 4,{\text{ }}x \in \mathbb{R}\).
The domain of \(f\) is now restricted to \([0,{\text{ }}a]\).
Let \(g(x) = 2\sin (x – 1) – 3,{\text{ }} – \frac{\pi }{2} + 1 \leqslant x \leqslant \frac{\pi }{2} + 1\).
a.Find the solutions of \(f(x) > 0\).[3]
b.For the curve \(y = f(x)\).
(i) Find the coordinates of both local minimum points.
(ii) Find the \(x\)-coordinates of the points of inflexion.[5]
c.i.Write down the largest value of \(a\) for which \(f\) has an inverse. Give your answer correct to 3 significant figures.[2]
c.ii.For this value of a sketch the graphs of \(y = f(x)\) and \(y = {f^{ – 1}}(x)\) on the same set of axes, showing clearly the coordinates of the end points of each curve.[2]
c.iii.Solve \({f^{ – 1}}(x) = 1\).[2]
d.i.Find an expression for \({g^{ – 1}}(x)\), stating the domain.[4]
d.ii.Solve \(({f^{ – 1}} \circ g)(x) < 1\).[4]
▶️Answer/Explanation
Markscheme
valid method eg, sketch of curve or critical values found (M1)
\(x < – 2.24,{\text{ }}x > 2.24,\) A1
\( – 1 < x < 0.8\) A1
Note: Award M1A1A0 for correct intervals but with inclusive inequalities.
[3 marks]
(i) \((1.67,{\text{ }} – 5.14),{\text{ }}( – 1.74,{\text{ }} – 3.71)\) A1A1
Note: Award A1A0 for any two correct terms.
(ii) \(f'(x) = 4{x^3} + 0.6{x^2} – 11.6x – 1\)
\(f”(x) = 12{x^2} + 1.2x – 11.6 = 0\) (M1)
\( – 1.03,{\text{ }}0.934\) A1A1
Note: M1 should be awarded if graphical method to find zeros of \(f”(x)\) or turning points of \(f'(x)\) is shown.
[5 marks]
1.67 A1
[2 marks]
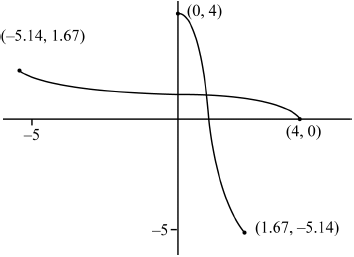 M1A1A1
M1A1A1
Note: Award M1 for reflection of their \(y = f(x)\) in the line \(y = x\) provided their \(f\) is one-one.
A1 for \((0,{\text{ }}4)\), \((4,{\text{ }}0)\) (Accept axis intercept values) A1 for the other two sets of coordinates of other end points
[2 marks]
\(x = f(1)\) M1
\( = – 1.6\) A1
[2 marks]
\(y = 2\sin (x – 1) – 3\)
\(x = 2\sin (y – 1) – 3\) (M1)
\(\left( {{g^{ – 1}}(x) = } \right){\text{ }}\arcsin \left( {\frac{{x + 3}}{2}} \right) + 1\) A1
\( – 5 \leqslant x \leqslant – 1\) A1A1
Note: Award A1 for −5 and −1, and A1 for correct inequalities if numbers are reasonable.
[8 marks]
\({f^{ – 1}}\left( {g(x)} \right) < 1\)
\(g(x) > – 1.6\) (M1)
\(x > {g^{ – 1}}( – 1.6) = 1.78\) (A1)
Note: Accept = in the above.
\(1.78 < x \leqslant \frac{\pi }{2} + 1\) A1A1
Note: A1 for \(x > 1.78\) (allow ≥) and A1 for \(x \leqslant \frac{\pi }{2} + 1\).
[4 marks]
Question
The polynomial
f(x) = x4 + ax3 + bx2 + cx + d
is divisible by (x – 1) and (x – 2). The sum of its roots is 7, the product of its roots is 0.
(a) Find the values of a, b, c and d
(b) Factorize f(x).
▶️Answer/Explanation
Ans
(a) Sum =\(-\frac{a}{1}=7\Rightarrow a = -7\), Product = \(\frac{d}{1}=0\Rightarrow d = 0\)
f(1) = 0 ⇒ 1 + a + b + c + d = 0 ⇒ b + c = 6
f(2) = 0 ⇒ 16 + 8a + 4b + 2c + d = 0⇒2b + c = 20
Therefore, b=14 c=-8
(b) We know three roots, 0, 1 and 2. Since the sum is -7 the third root is 4.
Hence f(x)=x(x-1)(x-2)(x-4)
Question
Consider the polynomial
f(x) = ax4 + bx3 + cx2 + dx + 16
When f(x) is divided by (x+1) the remainder is 120, while (x-1) is a factor. The sum and the product of its roots are both 8.
(a) Find the values of a, b, c and d.
When f(x) is divided by the factor (x-1) the quotient q(x) is a cubic function.
(b) Find the sum and the product of the roots of q(x)>
▶️Answer/Explanation
Ans
(a) a = 2 , b= –16, c= 42, d= –44
Indeed,
Product = \(\frac{13}{a}=8\Rightarrow a=2\) Sum =\(-\frac{b}{a}=8\Rightarrow b = -16\)
\(f(1)=0\Rightarrow a+b+c+d+16=0\Rightarrow c+d=-2\)
\(f(-1)=120\Rightarrow a-b+c-d+16=0\Rightarrow c-d=86\)
Therefore, c=42, d=-44
(b) Sum = 7, Product = 8
Question
The functions \(f\) and \(g\) are defined by
\[f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2},{\text{ }}x \in \mathbb{R}\]
\[g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2},{\text{ }}x \in \mathbb{R}\]
Let \(h(x) = nf(x) + g(x)\) where \(n \in \mathbb{R},{\text{ }}n > 1\).
Let \(t(x) = \frac{{g(x)}}{{f(x)}}\).
a.(i) Show that \(\frac{1}{{4f(x) – 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\).
(ii) Use the substitution \(u = {{\text{e}}^x}\) to find \(\int_0^{\ln 3} {\frac{1}{{4f(x) – 2g(x)}}} {\text{d}}x\). Give your answer in the form \(\frac{{\pi \sqrt a }}{b}\) where \(a,{\text{ }}b \in {\mathbb{Z}^ + }\).[9]
b.(i) By forming a quadratic equation in \({{\text{e}}^x}\), solve the equation \(h(x) = k\), where \(k \in {\mathbb{R}^ + }\).
(ii) Hence or otherwise show that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{n^2} – 1} \) and \(k \in {\mathbb{R}^ + }\).[8]
c.(i) Show that \(t'(x) = \frac{{{{[f(x)]}^2} – {{[g(x)]}^2}}}{{{{[f(x)]}^2}}}\) for \(x \in \mathbb{R}\).
(ii) Hence show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).[6]
▶️Answer/Explanation
Markscheme
(i) \(\frac{1}{{4\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right) – 2\left( {\frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}} \right)}}\) (M1)
\( = \frac{1}{{2({{\text{e}}^x} + {{\text{e}}^{ – x}}) – ({{\text{e}}^x} – {{\text{e}}^{ – x}})}}\) (A1)
\( = \frac{1}{{{{\text{e}}^x} + 3{{\text{e}}^{ – x}}}}\) A1
\( = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\) AG
(ii) \(u = {{\text{e}}^x} \Rightarrow {\text{d}}u = {{\text{e}}^x}{\text{d}}x\) A1
\(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) M1
(when \(x = 0,{\text{ }}u = 1\) and when \(x = \ln 3,{\text{ }}u = 3\))
\(\int_1^3 {\frac{1}{{{u^2} + 3}}{\text{d}}u\left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{u}{{\sqrt 3 }}} \right)} \right]_1^3} \) M1A1
\(\left( { = \left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{{{{\text{e}}^x}}}{{\sqrt 3 }}} \right)} \right]_0^{\ln 3}} \right)\)
\( = \frac{{\pi \sqrt 3 }}{9} – \frac{{\pi \sqrt 3 }}{{18}}\) (M1)
\( = \frac{{\pi \sqrt 3 }}{{18}}\) A1
[9 marks]
(i) \((n + 1){{\text{e}}^{2x}} – 2k{{\text{e}}^x} + (n – 1) = 0\) M1A1
\({{\text{e}}^x} = \frac{{2k \pm \sqrt {4{k^2} – 4({n^2} – 1)} }}{{2(n + 1)}}\) M1
\(x = \ln \left( {\frac{{k \pm \sqrt {{k^2} – {n^2} + 1} }}{{n + 1}}} \right)\) M1A1
(ii) for two real solutions, we require \(k > \sqrt {{k^2} – {n^2} + 1} \) R1
and we also require \({k^2} – {n^2} + 1 > 0\) R1
\({k^2} > {n^2} – 1\) A1
\( \Rightarrow k > \sqrt {{n^2} – 1} {\text{ }}({\text{ }}k \in {\mathbb{R}^ + })\) AG
[8 marks]
METHOD 1
\(t(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}\)
\(t'(x) = \frac{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2} – {{({{\text{e}}^x} – {{\text{e}}^{ – x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\) M1A1
\(t'(x) = \frac{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right)}^2} – {{\left( {\frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}} \right)}^2}}}{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right)}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 2
\(t'(x) = \frac{{f(x)g'(x) = g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 3
\(t(x) = ({{\text{e}}^x} – {{\text{e}}^{ – x}}){({{\text{e}}^x} + {{\text{e}}^{ – x}})^{ – 1}}\)
\(t'(x) = 1 – \frac{{{{({{\text{e}}^x} – {{\text{e}}^{ – x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\) M1A1
\( = 1 – \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 4
\(t'(x) = \frac{{g'(x)}}{{f(x)}} – \frac{{g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) gives \(t'(x) = 1 – \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
(ii) METHOD 1
\({\left[ {f(x)} \right]^2} > {\left[ {g(x)} \right]^2}\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ – x}}\) and \({{\text{e}}^x} – {{\text{e}}^{ – x}}\).
METHOD 2
\({\left[ {f(x)} \right]^2} – {\left[ {g(x)} \right]^2} = 1\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ – x}}\) and \({{\text{e}}^x} – {{\text{e}}^{ – x}}\).
METHOD 3
\(t'(x) = \frac{4}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\)
\({\left( {{{\text{e}}^x} + {{\text{e}}^{ – x}}} \right)^2} > 0\) M1A1
\(\frac{4}{{{{\left( {{{\text{e}}^x} + {{\text{e}}^{ – x}}} \right)}^2}}} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
[6 marks]
Examiners report
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
Part (a)(i) was reasonably well done with most candidates able to show that \(\frac{1}{{4f(x) – 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\). In part (a)(ii), a number of candidates correctly used the required substitution to obtain \(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) but then thought that the antiderivative involved natural log rather than arctan.
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
In part (b)(i), a reasonable number of candidates were able to form a quadratic in \({{\text{e}}^x}\) (involving parameters \(n\) and \(k\)) and then make some progress towards solving for \({{\text{e}}^x}\) in terms of \(n\) and \(k\). Having got that far, a small number of candidates recognised to then take the natural logarithm of both sides and hence solve \(h(x) = k\) for \(\chi \). In part (b)(ii), a small number of candidates were able to show from their solutions to part (b)(i) or through the use of the discriminant that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{k^2} – {n^2} + 1} \) and \(k > \sqrt {{n^2} – 1} \).
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
It was pleasing to see the number of candidates who attempted part (c). In part (c)(i), a large number of candidates were able to correctly apply either the quotient rule or the product rule to find \(t'(x)\). A smaller number of candidates were then able to show equivalence between the form of \(t'(x)\) they had obtained and the form of \(t'(x)\) required in the question. A pleasing number of candidates were able to exploit the property that \(f'(x) = g(x)\) and \(g'(x) = f(x)\). As with part (c)(i), part (c)(ii) could be successfully tackled in a number of ways. The best candidates offered concise logical reasoning to show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).
Question
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let \({\text{P}}(X = n)\) be the probability that Kati obtains her third voucher on the \(n{\text{th}}\) bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that \({\text{P}}(X = n) = \frac{{{n^2} + an + b}}{{2000}} \times {0.9^{n – 3}}\) for \(n \geqslant 3,{\text{ }}n \in \mathbb{N}\).
Kati’s mother goes to the shop and buys \(x\) chocolate bars. She takes the bars home for Kati to open.
a.Show that \({\text{P}}(X = 3) = 0.001\) and \({\text{P}}(X = 4) = 0.0027\).[3]
b.Find the values of the constants \(a\) and \(b\).[5]
c.Deduce that \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{0.9(n – 1)}}{{n – 3}}\) for \(n > 3\).[4]
d.(i) Hence show that \(X\) has two modes \({m_1}\) and \({m_2}\).
(ii) State the values of \({m_1}\) and \({m_2}\).[5]
e.Determine the minimum value of \(x\) such that the probability Kati receives at least one free gift is greater than 0.5.[3]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 3) = {(0.1)^3}\) A1
\( = 0.001\) AG
\({\text{P}}(X = 4) = {\text{P}}(VV\bar VV) + {\text{P}}(V\bar VVV) + {\text{P}}(\bar VVVV)\) (M1)
\( = 3 \times {(0.1)^3} \times 0.9\) (or equivalent) A1
\( = 0.0027\) AG
[3 marks]
METHOD 1
attempting to form equations in \(a\) and \(b\) M1
\(\frac{{9 + 3a + b}}{{2000}} = \frac{1}{{1000}}{\text{ }}(3a + b = – 7)\) A1
\(\frac{{16 + 4a + b}}{{2000}} \times \frac{9}{{10}} = \frac{{27}}{{10\,000}}{\text{ }}(4a + b = – 10)\) A1
attempting to solve simultaneously (M1)
\(a = – 3,{\text{ }}b = 2\) A1
METHOD 2
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) M1
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) (M1)A1
\( = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) A1
\(a = – 3,b = 2\) A1
Note: Condone the absence of \({0.9^{n – 3}}\) in the determination of the values of \(a\) and \(b\).
[5 marks]
METHOD 1
EITHER
\({\text{P}}(X = n) = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) (M1)
OR
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) (M1)
THEN
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) A1
\({\text{P}}(X = n – 1) = \frac{{(n – 2)(n – 3)}}{{2000}} \times {0.9^{n – 4}}\) A1
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{(n – 1)(n – 2)}}{{(n – 2)(n – 3)}} \times 0.9\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
METHOD 2
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{\frac{{{n^2} – 3n + 2}}{{2000}} \times {{0.9}^{n – 3}}}}{{\frac{{{{(n – 1)}^2} – 3(n – 1) + 2}}{{2000}} \times {{0.9}^{n – 4}}}}\) (M1)
\( = \frac{{0.9({n^2} – 3n + 2)}}{{({n^2} – 5n + 6)}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{0.9(n – 1)(n – 2)}}{{(n – 2)(n – 3)}}\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
[4 marks]
(i) attempting to solve \(\frac{{0.9(n – 1)}}{{n – 3}} = 1\) for \(n\) M1
\(n = 21\) A1
\(\frac{{0.9(n – 1)}}{{n – 3}} < 1 \Rightarrow n > 21\) R1
\(\frac{{0.9(n – 1)}}{{n – 3}} > 1 \Rightarrow n < 21\) R1
\(X\) has two modes AG
Note: Award R1R1 for a clearly labelled graphical representation of the two inequalities (using \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}}\)).
(ii) the modes are 20 and 21 A1
[5 marks]
METHOD 1
\(Y \sim {\text{B}}(x,{\text{ }}0.1)\) (A1)
attempting to solve \({\text{P}}(Y \geqslant 3) > 0.5\) (or equivalent eg \(1 – {\text{P}}(Y \leqslant 2) > 0.5\)) for \(x\) (M1)
Note: Award (M1) for attempting to solve an equality (obtaining \(x = 26.4\)).
\(x = 27\) A1
METHOD 2
\(\sum\limits_{n = 0}^x {{\text{P}}(X = n) > 0.5} \) (A1)
attempting to solve for \(x\) (M1)
\(x = 27\) A1
[3 marks]
Question
In the quadratic equation \(7{x^2} – 8x + p = 0,{\text{ }}(p \in \mathbb{Q})\), one root is three times the other root.
Find the value of \(p\).
▶️Answer/Explanation
Markscheme
METHOD 1
let roots be \(\alpha \) and \(3\alpha \) (M1)
sum of roots \((4\alpha ) = \frac{8}{7}\) M1
\( \Rightarrow \alpha = \frac{2}{7}\) A1
EITHER
product of roots \((3{\alpha ^2}) = \frac{p}{7}\) M1
\(p = 21{\alpha ^2} = 21 \times \frac{4}{{49}}\)
OR
\(7{\left( {\frac{2}{7}} \right)^2} – 8\left( {\frac{2}{7}} \right) + p = 0\) M1
\(\frac{4}{7} – \frac{{16}}{7} + p = 0\)
THEN
\( \Rightarrow p = \frac{{12}}{7}{\text{ }}( = 1.71)\) A1
METHOD 2
\(x = \frac{{8 \pm \sqrt {64 – 28p} }}{{14}}\) (M1)
\(\frac{{8 + \sqrt {64 – 28p} }}{{14}} = 3\left( {\frac{{8 – \sqrt {64 – 28p} }}{{14}}} \right)\) M1A1
\(8 + \sqrt {64 – 28p} = 24 – 3\sqrt {64 – 28p} \Rightarrow \sqrt {64 – 28p} = 4\) (M1)
\(p = \frac{{12}}{7}{\text{ }}( = 1.71)\) A1
[5 marks]
Examiners report
Question
The equation \({x^2} – 5x – 7 = 0\) has roots \(\alpha \) and \(\beta \). The equation \({x^2} + px + q = 0\) has roots \(\alpha + 1\) and \(\beta + 1\). Find the value of \(p\) and the value of \(q\).
▶️Answer/Explanation
Markscheme
METHOD 1
\(\alpha + \beta = 5,\,\,\alpha \beta = – 7\) (M1)(A1)
Note: Award M1A0 if only one equation obtained.
\(\left( {\alpha + 1} \right) + \left( {\beta + 1} \right) = 5 + 2 = 7\) A1
\(\left( {\alpha + 1} \right)\left( {\beta + 1} \right) = \alpha \beta + \left( {\alpha + \beta } \right) + 1\) (M1)
\( = – 7 + 5 + 1 = – 1\)
\(p = – 7,\,\,q = – 1\) A1A1
METHOD 2
\(\alpha = \frac{{5 + \sqrt {53} }}{2} = 6.1 \ldots {\text{;}}\,\,\beta = \frac{{5 – \sqrt {53} }}{2} = – 1.1 \ldots \) (M1)(A1)
\(\alpha + 1 = \frac{{7 + \sqrt {53} }}{2} = 7.1 \ldots {\text{;}}\,\,\beta + 1 = \frac{{7 – \sqrt {53} }}{2} = – 0.1 \ldots \) A1
\(\left( {x – 7.14 \ldots } \right)\left( {x + 0.14 \ldots } \right) = {x^2} – 7x – 1\) (M1)
\(p = – 7,\,\,q = – 1\) A1A1
Note: Exact answers only.
[6 marks]