Download IITian Academy App for accessing Online Mock Tests and More..
Question
The sum of the first 16 terms of an arithmetic sequence is 212 and the fifth term is 8.
Find the first term and the common difference.
Find the smallest value of n such that the sum of the first n terms is greater than 600.
Answer/Explanation
Markscheme
\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)
\(212 = \frac{{16}}{2}(2a + 15d)\,\,\,\,\,( = 16a + 120d)\) A1
\({n^{th}}{\text{ term is }}a + (n – 1)d\)
\(8 = a + 4d\) A1
solving simultaneously: (M1)
\(d = 1.5,{\text{ }}a = 2\) A1
[4 marks]
\(\frac{n}{2}[4 + 1.5(n – 1)] > 600\) (M1)
\( \Rightarrow 3{n^2} + 5n – 2400 > 0\) (A1)
\( \Rightarrow n > 27.4…,{\text{ }}(n < – 29.1…)\)
Note: Do not penalize improper use of inequalities.
\( \Rightarrow n = 28\) A1
[3 marks]
Examiners report
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
Question
A function \(f\) is defined by \(f(x) = (x + 1)(x-1)(x-5),{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(f(x) < \left| {f(x)} \right|\).
A function \(g\) is defined by \(g(x) = {x^2} + x – 6,{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(g(x) < \frac{1}{{g(x)}}\).
Answer/Explanation
Markscheme
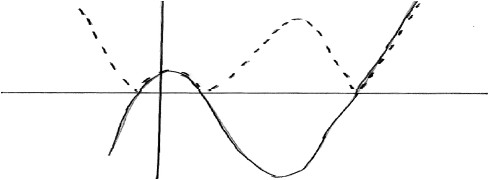
as roots of \(f(x) = 0\) are \( – 1,{\text{ }}1,{\text{ }}5\) (M1)
solution is \(\left] { – \infty ,{\text{ }} – 1} \right[ \cup \left] {1,{\text{ }}5} \right[\;\;\;(x < – 1\;\;\;{\text{or}}\;\;\;1 < x < 5)\) A1A1
Note: Award A1A0 for closed intervals.
[3 marks]
METHOD 1
\(\left( {{\text{graphs of }}g(x){\text{ and }}\frac{1}{{g(x)}}} \right)\)
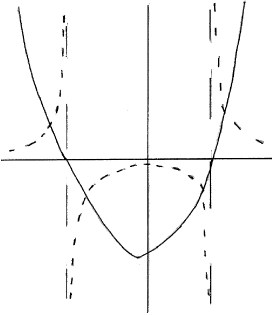
roots of \(g(x) = 0\) are \( – 3\) and 2 (M1)(A1)
Notes: Award M1 if quadratic graph is drawn or two roots obtained.
Roots may be indicated anywhere eg asymptotes on graph or in inequalities below.
the intersections of the graphs \(g(x)\) and of \(1/g(x)\)
are \( – 3.19,{\text{ }} – 2.79,{\text{ }}1.79,{\text{ 2.19}}\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is \(\left] { – 3.19,{\text{ }} – 3} \right[ \cup \left] { – 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( – 3.19 < x < – 3\;\;\;{\text{or}}\;\;\; – 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
METHOD 2
\(\left( {{\text{graph of }}g(x) – \frac{1}{{g(x)}}} \right)\)
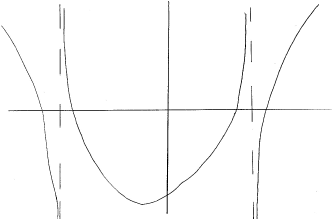
asymptotes at \(x = – 3\) and \(x = 2\) (M1)(A1)
Note: May be indicated on the graph.
roots of graph are \( – 3.19,{\text{ }} – 2.79,{\text{ }}1.79,{\text{ }}2.19\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is (when graph is negative)
\(\left] { – 3.19,{\text{ }} – 3} \right[ \cup \left] { – 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( – 3.19 < x < – 3\;\;\;{\text{or}}\;\;\; – 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
[7 marks]
Total [10 marks]
Examiners report
In general part (a) was performed correctly, with the vast majority of candidates stating the correct open intervals as required.
In part (b) many candidates scored a few marks by just finding intersection points and equations of asymptotes; many other candidates showed difficulties in manipulating inequalities and ignored the fact that the quantities could be negative. Candidates that used the graph well managed to achieve full marks. Unfortunately many sketches were very crudely drawn hence they were of limited value for assessment purposes.