Question
Two non-intersecting circles C1 , containing points M and S , and C2 , containing points N and R, have centres P and Q where PQ \( = 50\) . The line segments [MN] and [SR] are common tangents to the circles. The size of the reflex angle MPS is \( \alpha\), the size of the obtuse angle NQR is \( \beta\) , and the size of the angle MPQ is \( \theta\) . The arc length MS is \({l_1}\) and the arc length NR is \({l_2}\) . This information is represented in the diagram below.
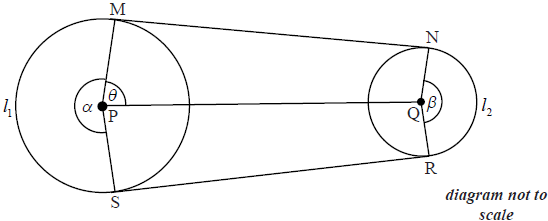
The radius of C1 is \(x\) , where \(x \geqslant 10\) and the radius of C2 is \(10\).
(a) Explain why \(x < 40\) .
(b) Show that cosθ = x −10 50.
(c) (i) Find an expression for MN in terms of \(x\) .
(ii) Find the value of \(x\) that maximises MN.
(d) Find an expression in terms of \(x\) for
(i) \( \alpha\) ;
(ii) \( \beta\) .
(e) The length of the perimeter is given by \({l_1} + {l_2} + {\text{MN}} + {\text{SR}}\).
(i) Find an expression, \(b (x)\) , for the length of the perimeter in terms of \(x\) .
(ii) Find the maximum value of the length of the perimeter.
(iii) Find the value of \(x\) that gives a perimeter of length \(200\).
▶️Answer/Explanation
Markscheme
(a) PQ \( = 50\) and non-intersecting R1
[1 mark]
(b) a construction QT (where T is on the radius MP), parallel to MN, so that \({\text{Q}}\hat {\text{T}}{\text{M}} = 90^\circ \) (angle between tangent and radius \( = 90^\circ \) ) M1
lengths \(50\), \(x – 10\) and angle \( \theta\) marked on a diagram, or equivalent R1
Note: Other construction lines are possible.
[2 marks]
(c) (i) MN \( = \sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1
(ii) maximum for MN occurs when \(x = 10\) A1
[2 marks]
(d) (i) \(\alpha = 2\pi – 2\theta \) M1
\( = 2\pi – 2\arccos \left( {\frac{{x – 10}}{{50}}} \right)\) A1
(ii) \(\beta = 2\pi – \alpha \) ( \( = 2\theta \) ) A1
\( = 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)\) A1
[4 marks]
(e) (i) \(b(x) = x\alpha + 10\beta + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) A1A1A1
\( = x\left( {2\pi – 2\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 20\left( {\left( {{{\cos }^{ – 1}}\left( {\frac{{x – 10}}{{50}}} \right)} \right)} \right) + 2\sqrt {{{50}^2} – {{\left( {x – 10} \right)}^2}} \) M1A1
(ii) maximum value of perimeter \( = 276\) A2
(iii) perimeter of \(200\) cm \(b(x) = 200\) (M1)
when \(x = 21.2\) A1
[9 marks]
Total [18 marks]
Examiners report
This is not an inherently difficult question, but candidates either made heavy weather of it or avoided it almost entirely. The key to answering the question is in obtaining the displayed answer to part (b), for which a construction line parallel to MN through Q is required. Diagrams seen by examiners on some scripts tend to suggest that the perpendicularity property of a tangent to a circle and the associated radius is not as firmly known as they had expected. Some candidates mixed radians and degrees in their expressions.
Question
The diagram below shows two concentric circles with centre O and radii 2 cm and 4 cm.
The points P and Q lie on the larger circle and \({\rm{P}}\hat {\text{O}}{\text{Q}} = x\) , where \(0 < x < \frac{\pi }{2}\) .
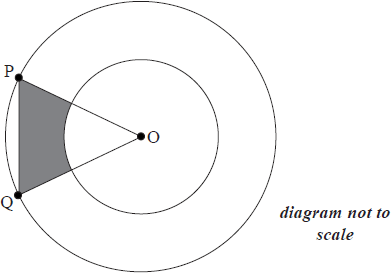
(a) Show that the area of the shaded region is \(8\sin x – 2x\) .
(b) Find the maximum area of the shaded region.
▶️Answer/Explanation
Markscheme
(a) shaded area area of triangle area of sector, i.e. (M1)
\(\left( {\frac{1}{2} \times {4^2}\sin x} \right) – \left( {\frac{1}{2}{2^2}x} \right) = 8\sin x – 2x\) A1A1AG
(b) EITHER
any method from GDC gaining \(x \approx 1.32\) (M1)(A1)
maximum value for given domain is \(5.11\) A2
OR
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 8\cos x – 2\) A1
set \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\), hence \(8\cos x – 2 = 0\) M1
\(\cos x = \frac{1}{4} \Rightarrow x \approx 1.32\) A1
hence \({A_{\max }} = 5.11\) A1
[7 marks]
Examiners report
Generally a well answered question.
Question
The interior of a circle of radius 2 cm is divided into an infinite number of sectors. The areas of these sectors form a geometric sequence with common ratio k. The angle of the first sector is \(\theta \) radians.
(a) Show that \(\theta = 2\pi (1 – k)\).
(b) The perimeter of the third sector is half the perimeter of the first sector.
Find the value of k and of \(\theta \).
▶️Answer/Explanation
Markscheme
(a) the area of the first sector is \(\frac{1}{2}{2^2}\theta \) (A1)
the sequence of areas is \(2\theta ,{\text{ }}2k\theta ,{\text{ }}2{k^2}\theta \ldots \) (A1)
the sum of these areas is \(2\theta (1 + k + {k^2} + \ldots )\) (M1)
\( = \frac{{2\theta }}{{1 – k}} = 4\pi \) M1A1
hence \(\theta = 2\pi (1 – k)\) AG
Note: Accept solutions where candidates deal with angles instead of area.
[5 marks]
(b) the perimeter of the first sector is \(4 + 2\theta \) (A1)
the perimeter of the third sector is \(4 + 2{k^2}\theta \) (A1)
the given condition is \(4 + 2{k^2}\theta = 2 + \theta \) M1
which simplifies to \(2 = \theta (1 – 2{k^2})\) A1
eliminating \(\theta \), obtain cubic in k: \(\pi (1 – k)(1 – 2{k^2}) – 1 = 0\) A1
or equivalent
solve for k = 0.456 and then \(\theta = 3.42\) A1A1
[7 marks]
Total [12 marks]
Examiners report
This was a disappointingly answered question.
Part(a) – Many candidates correctly assumed that the areas of the sectors were proportional to their angles, but did not actually state that fact.
Part(b) – Few candidates seem to know what the term ‘perimeter’ means.
Question
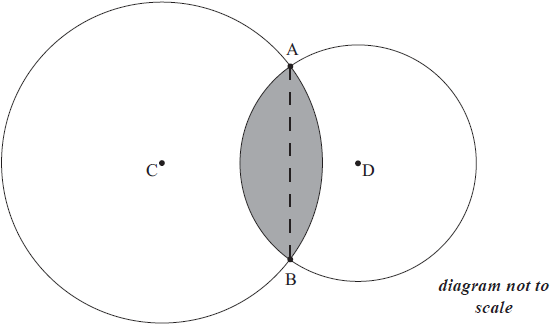
The radius of the circle with centre C is 7 cm and the radius of the circle with centre D is 5 cm. If the length of the chord [AB] is 9 cm, find the area of the shaded region enclosed by the two arcs AB.
▶️Answer/Explanation
Markscheme
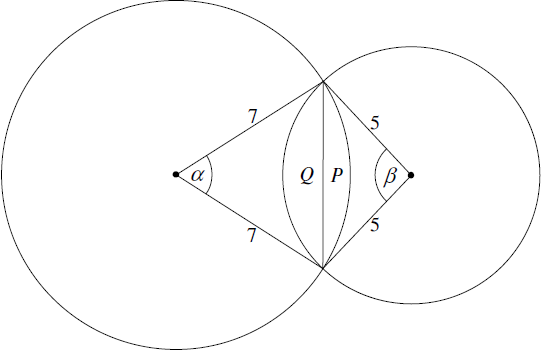
\(\alpha = 2\arcsin \left( {\frac{{4.5}}{7}} \right)\) (\( \Rightarrow \alpha = 1.396… = 80.010^\circ …\)) M1(A1)
\(\beta = 2\arcsin \left( {\frac{{4.5}}{5}} \right)\) (\( \Rightarrow \beta = 2.239… = 128.31^\circ …\)) (A1)
Note: Allow use of cosine rule.
area \(P = \frac{1}{2} \times {7^2} \times \left( {\alpha – \sin \alpha } \right) = 10.08…\) M1(A1)
area \(Q = \frac{1}{2} \times {5^2} \times \left( {\beta – \sin \beta } \right) = 18.18…\) (A1)
Note: The M1 is for an attempt at area of sector minus area of triangle.
Note: The use of degrees correctly converted is acceptable.
area = 28.3 (cm2) A1
[7 marks]
Examiners report
Whilst most candidates were able to make the correct construction to solve the problem some candidates seemed unable to find the area of a segment. In a number of cases candidates used degrees in a formula that required radians. There were a number of candidates who followed a completely correct method but due to premature approximation were unable to obtain a correct solution.
Question
Two discs, one of radius 8 cm and one of radius 5 cm, are placed such that they touch each other. A piece of string is wrapped around the discs. This is shown in the diagram below.
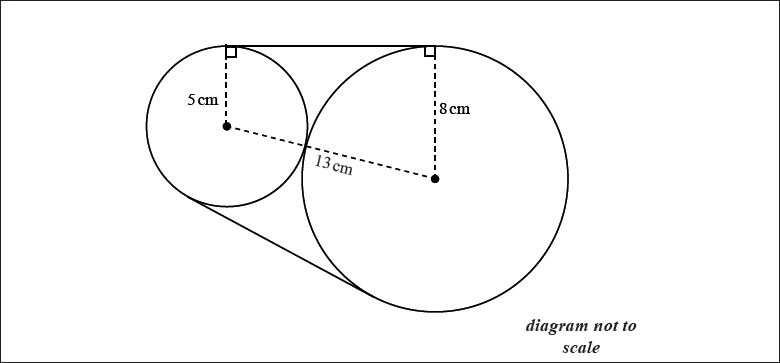
Calculate the length of string needed to go around the discs.
▶️Answer/Explanation
Markscheme
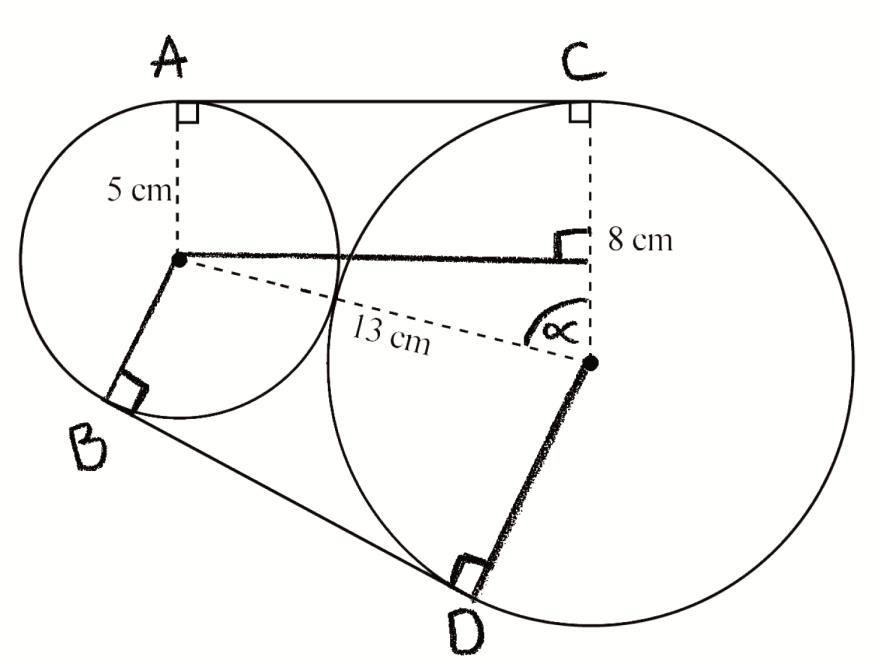
\({\text{AC}} = {\text{BD}} = \sqrt {{{13}^2} – {3^2}} = 12.64…\) (A1)
\(\cos \alpha = \frac{3}{{13}} \Rightarrow \alpha = 1.337…(76.65…^\circ .)\) (M1)(A1)
attempt to find either arc length AB or arc length CD (M1)
\({\text{arc length AB}} = 5(\pi – 2 \times 0.232…){\text{ }}( = 13.37…)\) (A1)
\({\text{arc length CD}} = 8(\pi + 2 \times 0.232…){\text{ }}( = 28.85…)\) (A1)
length of string = 13.37… + 28.85… + 2(12.64…) (M1)
= 67.5 (cm) A1
[8 marks]
Examiners report
Given that this was the last question in section A it was pleasing to see a good number of candidates make a start on the question. As would be expected from a question at this stage of the paper, more limited numbers of candidates gained full marks. A number of candidates made the question very difficult by unnecessarily splitting the angles required to find the final answer into combinations of smaller angles, all of which required a lot of work and time.
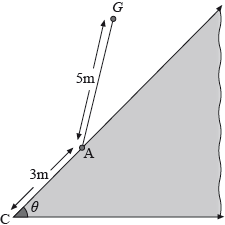
Question
The diagram below shows a fenced triangular enclosure in the middle of a large grassy field. The points A and C are 3 m apart. A goat \(G\) is tied by a 5 m length of rope at point A on the outside edge of the enclosure.
Given that the corner of the enclosure at C forms an angle of \(\theta \) radians and the area of field that can be reached by the goat is \({\text{44 }}{{\text{m}}^{\text{2}}}\), find the value of \(\theta \).
▶️Answer/Explanation
Markscheme
attempting to use the area of sector formula (including for a semicircle) M1
semi-circle \(\frac{1}{2}\pi \times {5^2} = \frac{{25\pi }}{2} = 39.26990817 \ldots \) (A1)
angle in smaller sector is \(\pi – \theta \) (A1)
area of sector \( = \frac{1}{2} \times {2^2} \times (\pi – \theta )\) (A1)
attempt to total a sum of areas of regions to 44 (M1)
\(2(\pi – \theta ) = 44 – 39.26990817 \ldots \)
\(\theta = 0.777{\text{ }}\left( { = \frac{{29\pi }}{4} – 22} \right)\) A1
Note: Award all marks except the final A1 for correct working in degrees.
Note: Attempt to solve with goat inside triangle should lead to nonsense answer and so should only receive a maximum of the two M marks.
[6 marks]
Examiners report
Many students experienced difficulties with this question, mostly it seems through failing to understand the question. Some students left their answers in degrees, thereby losing the final mark.
Question
This diagram shows a metallic pendant made out of four equal sectors of a larger circle of radius \({\text{OB}} = 9{\text{ cm}}\) and four equal sectors of a smaller circle of radius \({\text{OA}} = 3{\text{ cm}}\).
The angle \({\text{BOC}} = \) 20°.
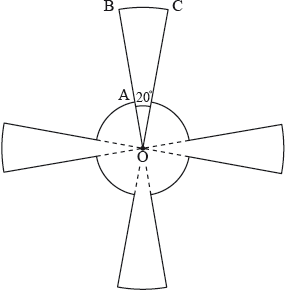
Find the area of the pendant.
▶️Answer/Explanation
Markscheme
METHOD 1
area = (four sector areas radius 9) + (four sector areas radius 3) (M1)
\( = 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) + 4\left( {\frac{1}{2}{3^2}\frac{{7\pi }}{{18}}} \right)\) (A1)(A1)
\( = 18\pi + 7\pi \)
\( = 25\pi {\text{ }}( = 78.5{\text{ c}}{{\text{m}}^2})\) A1
METHOD 2
area =
(area of circle radius 3) + (four sector areas radius 9) – (four sector areas radius 3) (M1)
\(\pi {3^2} + 4\left( {\frac{1}{2}{9^2}\frac{\pi }{9}} \right) – 4\left( {\frac{1}{2}{3^2}\frac{\pi }{9}} \right)\) (A1)(A1)
Note: Award A1 for the second term and A1 for the third term.
\( = 9\pi + 18\pi – 2\pi \)
\( = 25\pi {\text{ }}( = {\text{ }}78.5{\text{ c}}{{\text{m}}^2})\) A1
Note: Accept working in degrees.
[4 marks]