| Marks available | 1 |
| Reference code | 11N.1.hl.TZ0.4 |
Question
Given that \(f(x) = 1 + \sin x,{\text{ }}0 \leqslant x \leqslant \frac{{3\pi }}{2}\),
sketch the graph of \(f\);

show that \({\left( {f(x)} \right)^2} = \frac{3}{2} + 2\sin x – \frac{1}{2}\cos 2x\);
find the volume of the solid formed when the graph of f is rotated through \(2\pi \) radians about the x-axis.
Markscheme
 A1
A1
[1 mark]
\({(1 + \sin x)^2} = 1 + 2\sin x + {\sin ^2}x\)
\( = 1 + 2\sin x + \frac{1}{2}(1 – \cos 2x)\) A1
\( = \frac{3}{2} + 2\sin x – \frac{1}{2}\cos 2x\) AG
[1 mark]
\(V = \pi \int_0^{\frac{{3\pi }}{2}} {{{(1 + \sin x)}^2}{\text{d}}x} \) (M1)
\( = \pi \int_0^{\frac{{3\pi }}{2}} {\left( {\frac{3}{2} + 2\sin x – \frac{1}{2}\cos 2x} \right){\text{d}}x} \)
\( = \pi \left[ {\frac{3}{2}x – 2\cos x – \frac{{\sin 2x}}{4}} \right]_0^{\frac{{3\pi }}{2}}\) A1
\( = \frac{{9{\pi ^2}}}{4} + 2\pi \) A1A1
[4 marks]
Examiners report
Parts (a) and (b) were almost invariably correctly answered by candidates. In (c), most errors involved the integration of \(\cos (2x)\) and the insertion of the limits.
Parts (a) and (b) were almost invariably correctly answered by candidates. In (c), most errors involved the integration of \(\cos (2x)\) and the insertion of the limits.
Parts (a) and (b) were almost invariably correctly answered by candidates. In (c), most errors involved the integration of \(\cos (2x)\) and the insertion of the limits.
| Marks available | 8 |
| Reference code | 12M.1.hl.TZ1.10 |
Question
In the triangle ABC, \({\rm{A\hat BC}} = 90^\circ\) , \({\text{AC}} = \sqrt {\text{2}}\) and AB = BC + 1.
Show that cos \(\hat A – \sin \hat A = \frac{1}{{\sqrt 2 }}\).
By squaring both sides of the equation in part (a), solve the equation to find the angles in the triangle.
Apply Pythagoras’ theorem in the triangle ABC to find BC, and hence show that \(\sin \hat A = \frac{{\sqrt 6 – \sqrt 2 }}{4}\).
Hence, or otherwise, calculate the length of the perpendicular from B to [AC].
Markscheme
\(\cos \hat A = \frac{{{\text{BA}}}}{{\sqrt 2 }}\) A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }}\) A1
\(\cos \hat A – \sin \hat A = \frac{{{\text{BA}} – {\text{BC}}}}{{\sqrt 2 }}\) R1
\( = \frac{1}{{\sqrt 2 }}\) AG
[3 marks]
\({\cos ^2}\hat A – 2\cos \hat A\sin \hat A + {\sin ^2}\hat A = \frac{1}{2}\) M1A1
\(1 – 2\sin \hat A\cos \hat A = \frac{1}{2}\) M1A1
\(\sin 2\hat A = \frac{1}{2}\) M1
\(2\hat A = 30^\circ \) A1
angles in the triangle are 15° and 75° A1A1
Note: Accept answers in radians.
[8 marks]
\({\text{B}}{{\text{C}}^2} + {({\text{BC}} + 1)^2} = 2\) M1A1
\(2{\text{B}}{{\text{C}}^2} + 2{\text{BC}} – 1 = 0\) A1
\({\text{BC}} = \frac{{ -2 + \sqrt {12} }}{4}\left( { = \frac{{\sqrt 3 – 1}}{2}} \right)\) M1A1
\(\sin \hat A = \frac{{{\text{BC}}}}{{\sqrt 2 }} = \frac{{\sqrt 3 – 1}}{{2\sqrt 2 }}\) A1
\( = \frac{{\sqrt 6 – \sqrt 2 }}{4}\) AG
[6 marks]
EITHER
\(h = {\text{ABsin}}\hat A\) M1
\( = ({\text{BC}} + 1)\sin \hat A\) A1
\( = \frac{{\sqrt 3 + 1}}{2} \times \frac{{\sqrt 6 – \sqrt 2 }}{4} = \frac{{\sqrt 2 }}{4}\) M1A1
OR
\(\tfrac{1}{2}AB.BC = \tfrac{1}{2}AC.h\) M1
\(\frac{{\sqrt 3 – 1}}{2} \cdot \frac{{\sqrt {3 + 1} }}{2} = \sqrt {2h} \) A1
\(\frac{2}{4} = \sqrt 2 h\) M1
\(h = \frac{1}{{2\sqrt 2 }}\) A1
[4 marks]
Examiners report
Many good solutions to this question, although some students incorrectly stated the value of \(\arcsin \left( {\frac{1}{2}} \right)\). A surprising number of students had greater difficulties with part (d).
Many good solutions to this question, although some students incorrectly stated the value of \(\arcsin \left( {\frac{1}{2}} \right)\). A surprising number of students had greater difficulties with part (d).
Many good solutions to this question, although some students incorrectly stated the value of \(\arcsin \left( {\frac{1}{2}} \right)\). A surprising number of students had greater difficulties with part (d).
Many good solutions to this question, although some students incorrectly stated the value of \(\arcsin \left( {\frac{1}{2}} \right)\). A surprising number of students had greater difficulties with part (d).
| Marks available | 5 |
| Reference code | 12M.1.hl.TZ2.2 |
Question
Find the values of x for which the vectors \(\left( {\begin{array}{*{20}{c}}
1 \\
{2\cos x} \\
0
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
{ – 1} \\
{2\sin x} \\
1
\end{array}} \right)\) are perpendicular, \(0 \leqslant x \leqslant \frac{\pi }{2}\).
Markscheme
perpendicular when \(\left( {\begin{array}{*{20}{c}}
1 \\
{2\cos x} \\
0
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{2\sin x} \\
1
\end{array}} \right) = 0\) (M1)
\( \Rightarrow -1 + 4\sin x\cos x = 0\) A1
\( \Rightarrow \sin 2x = \frac{1}{2}\) M1
\( \Rightarrow 2x = \frac{\pi }{6},\frac{{5\pi }}{6}\)
\( \Rightarrow x = \frac{\pi }{{12}},\frac{{5\pi }}{{12}}\) A1A1
Note: Accept answers in degrees.
[5 marks]
Examiners report
Most candidates realised that the scalar product should be used to solve this problem and many obtained the equation \(4\sin x\cos x = 1\). Candidates who failed to see that this could be written as \(\sin 2x = 0.5\) usually made no further progress. The majority of those candidates who used this double angle formula carried on to obtain the solution \(\frac{\pi }{{12}}\) but few candidates realised that \(\frac{{5\pi }}{{12}}\) was also a solution.
| Marks available | 6 |
| Reference code | 12M.1.hl.TZ2.9 |
Question
Show that \(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\) .
Markscheme
METHOD 1
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \sec 2A + \tan 2A\)
consider right hand side
\(\sec 2A + \tan 2A = \frac{1}{{\cos 2A}} + \frac{{\sin 2A}}{{\cos 2A}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for recognizing the need for single angles and A1 for recognizing \({\cos ^2}A + {\sin ^2}A = 1\) .
\( = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{\cos A + \sin A}}{{\cos A – \sin A}}\) AG
METHOD 2
\(\frac{{\cos A + \sin A}}{{\cos A – \sin A}} = \frac{{{{(\cos A + \sin A)}^2}}}{{(\cos A + \sin A)(\cos A – \sin A)}}\) M1A1
\( = \frac{{{{\cos }^2}A + 2\sin A\cos A + {{\sin }^2}A}}{{{{\cos }^2}A – {{\sin }^2}A}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
\( = \frac{{1 + \sin 2A}}{{\cos 2A}}\) M1A1
\( = \sec 2A + \tan 2A\) AG
[6 marks]
Examiners report
Solutions to this question were good in general with many candidates realising that multiplying the numerator and denominator by \((\cos A + \sin A)\) might be helpful.
| Marks available | 4 |
| Reference code | 12N.1.hl.TZ0.1 |
Question
Given that \(\frac{\pi }{2} < \alpha < \pi \) and \(\cos \alpha = – \frac{3}{4}\), find the value of sin 2α .
Markscheme
\(\sin \alpha = \sqrt {1 – {{\left( { – \frac{3}{4}} \right)}^2}} = \frac{{\sqrt 7 }}{4}\) (M1)A1
attempt to use double angle formula M1
\(\sin 2\alpha = 2\frac{{\sqrt 7 }}{4}\left( { – \frac{3}{4}} \right) = – \frac{{3\sqrt 7 }}{8}\) A1
Note: \(\frac{{\sqrt 7 }}{4}\) seen would normally be awarded M1A1.
[4 marks]
Examiners report
Many candidates scored full marks on this question, though their explanations for part a) often lacked clarity. Most preferred to use some kind of right-angled triangle rather than (perhaps in this case) the more sensible identity \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
| Marks available | 2 |
| Reference code | 14M.1.hl.TZ1.5 |
Question
Use the identity \(\cos 2\theta = 2{\cos ^2}\theta – 1\) to prove that \(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} ,{\text{ }}0 \leqslant x \leqslant \pi \).
Find a similar expression for \(\sin \frac{1}{2}x,{\text{ }}0 \leqslant x \leqslant \pi \).
Hence find the value of \(\int_0^{\frac{\pi }{2}} {\left( {\sqrt {1 + \cos x} + \sqrt {1 – \cos x} } \right){\text{d}}x} \).
Markscheme
\(\cos x = 2{\cos ^2}\frac{1}{2}x – 1\)
\(\cos \frac{1}{2}x = \pm \sqrt {\frac{{1 + \cos x}}{2}} \) M1
positive as \(0 \leqslant x \leqslant \pi \) R1
\(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} \) AG
[2 marks]
\(\cos 2\theta = 1 – 2{\sin ^2}\theta \) (M1)
\(\sin \frac{1}{2}x = \sqrt {\frac{{1 – \cos x}}{2}} \) A1
[2 marks]
\(\sqrt 2 \int_0^{\frac{\pi }{2}} {\cos \frac{1}{2}x + \sin \frac{1}{2}x{\text{d}}x} \) A1
\( = \sqrt 2 \left[ {2\sin \frac{1}{2}x – 2\cos \frac{1}{2}x} \right]_0^{\frac{\pi }{2}}\) A1
\( = \sqrt 2 (0) – \sqrt 2 (0 – 2)\) A1
\( = 2\sqrt 2 \) A1
[4 marks]
Examiners report
| Marks available | 2 |
| Reference code | 14M.1.hl.TZ1.5 |
Question
Use the identity \(\cos 2\theta = 2{\cos ^2}\theta – 1\) to prove that \(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} ,{\text{ }}0 \leqslant x \leqslant \pi \).
Find a similar expression for \(\sin \frac{1}{2}x,{\text{ }}0 \leqslant x \leqslant \pi \).
Hence find the value of \(\int_0^{\frac{\pi }{2}} {\left( {\sqrt {1 + \cos x} + \sqrt {1 – \cos x} } \right){\text{d}}x} \).
Markscheme
\(\cos x = 2{\cos ^2}\frac{1}{2}x – 1\)
\(\cos \frac{1}{2}x = \pm \sqrt {\frac{{1 + \cos x}}{2}} \) M1
positive as \(0 \leqslant x \leqslant \pi \) R1
\(\cos \frac{1}{2}x = \sqrt {\frac{{1 + \cos x}}{2}} \) AG
[2 marks]
\(\cos 2\theta = 1 – 2{\sin ^2}\theta \) (M1)
\(\sin \frac{1}{2}x = \sqrt {\frac{{1 – \cos x}}{2}} \) A1
[2 marks]
\(\sqrt 2 \int_0^{\frac{\pi }{2}} {\cos \frac{1}{2}x + \sin \frac{1}{2}x{\text{d}}x} \) A1
\( = \sqrt 2 \left[ {2\sin \frac{1}{2}x – 2\cos \frac{1}{2}x} \right]_0^{\frac{\pi }{2}}\) A1
\( = \sqrt 2 (0) – \sqrt 2 (0 – 2)\) A1
\( = 2\sqrt 2 \) A1
[4 marks]
Examiners report
| Marks available | 6 |
| Reference code | 14M.1.hl.TZ1.10 |
Question
Given that \(\sin x + \cos x = \frac{2}{3}\), find \(\cos 4x\).
Markscheme
\({\sin ^2}x + {\cos ^2}x + 2\sin x\cos x = \frac{4}{9}\) (M1)(A1)
using \({\sin ^2}x + {\cos ^2}x = 1\) (M1)
\(2\sin x\cos x = – \frac{5}{9}\)
using \(2\sin x\cos x = \sin 2x\) (M1)
\(\sin 2x = – \frac{5}{9}\)
\(\cos 4x = 1 – 2{\sin ^2}2x\) M1
Note: Award this M1 for decomposition of cos 4x using double angle formula anywhere in the solution.
\( = 1 – 2 \times \frac{{25}}{{81}}\)
\( = \frac{{31}}{{81}}\) A1
[6 marks]
Examiners report
| Marks available | 7 |
| Reference code | 14M.1.hl.TZ2.9 |
Question
The first three terms of a geometric sequence are \(\sin x,{\text{ }}\sin 2x\) and \(4\sin x{\cos ^2}x,{\text{ }} – \frac{\pi }{2} < x < \frac{\pi }{2}\).
(a) Find the common ratio r.
(b) Find the set of values of x for which the geometric series \(\sin x + \sin 2x + 4\sin x{\cos ^2}x + \ldots \) converges.
Consider \(x = \arccos \left( {\frac{1}{4}} \right),{\text{ }}x > 0\).
(c) Show that the sum to infinity of this series is \(\frac{{\sqrt {15} }}{2}\).
Markscheme
(a) \(\sin x,{\text{ }}\sin 2x{\text{ and }}4\sin x{\cos ^2}x\)
\(r = \frac{{2\sin x\cos x}}{{\sin x}} = 2\cos x\) A1
Note: Accept \(\frac{{\sin 2x}}{{\sin x}}\).
[1 mark]
(b) EITHER
\(\left| r \right| < 1 \Rightarrow \left| {2\cos x} \right| < 1\) M1
OR
\( – 1 < r < 1 \Rightarrow – 1 < 2\cos x < 1\) M1
THEN
\(0 < \cos x < \frac{1}{2}{\text{ for }} – \frac{\pi }{2} < x < \frac{\pi }{2}\)
\( – \frac{\pi }{2} < x < – \frac{\pi }{3}{\text{ or }}\frac{\pi }{3} < x < \frac{\pi }{2}\) A1A1
[3 marks]
(c) \({S_\infty } = \frac{{\sin x}}{{1 – 2\cos x}}\) M1
\({S_\infty } = \frac{{\sin \left( {\arccos \left( {\frac{1}{4}} \right)} \right)}}{{1 – 2\cos \left( {\arccos \left( {\frac{1}{4}} \right)} \right)}}\)
\( = \frac{{\frac{{\sqrt {15} }}{4}}}{{\frac{1}{2}}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
\( = \frac{{\sqrt {15} }}{2}\) AG
[3 marks]
Total [7 marks]
Examiners report
| Marks available | 13 |
| Reference code | 14N.1.hl.TZ0.13 |
Question
(i) Show that \({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = \frac{{2\cos n\theta }}{{{{\cos }^n}\theta }},\;\;\;\cos \theta \ne 0\).
(ii) Hence verify that \({\text{i}}\tan \frac{{3\pi }}{8}\) is a root of the equation \({(1 + z)^4} + {(1 – z)^4} = 0,\;\;\;z \in \mathbb{C}\).
(iii) State another root of the equation \({(1 + z)^4} + {(1 – z)^4} = 0,\;\;\;z \in \mathbb{C}\).
(i) Use the double angle identity \(\tan 2\theta = \frac{{2\tan \theta }}{{1 – {{\tan }^2}\theta }}\) to show that \(\tan \frac{\pi }{8} = \sqrt 2 – 1\).
(ii) Show that \(\cos 4x = 8{\cos ^4}x – 8{\cos ^2}x + 1\).
(iii) Hence find the value of \(\int_0^{\frac{\pi }{8}} {\frac{{2\cos 4x}}{{{{\cos }^2}x}}{\text{d}}x} \).
Markscheme
(i) METHOD 1
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = {\left( {1 + {\text{i}}\frac{{\sin \theta }}{{\cos \theta }}} \right)^n} + {\left( {1 – {\text{i}}\frac{{\sin \theta }}{{\cos \theta }}} \right)^n}\) M1
\( = {\left( {\frac{{\cos \theta + i\sin \theta }}{{\cos \theta }}} \right)^n} + {\left( {\frac{{\cos \theta – i\sin \theta }}{{\cos \theta }}} \right)^n}\) A1
by de Moivre’s theorem (M1)
\({\left( {\frac{{\cos \theta + i\sin \theta }}{{\cos \theta }}} \right)^n} = \frac{{\cos n\theta + i\sin n\theta }}{{{{\cos }^n}\theta }}\) A1
recognition that \(\cos \theta – i\sin \theta \) is the complex conjugate of \(\cos \theta + i\sin \theta \) (R1)
use of the fact that the operation of complex conjugation commutes with the operation of raising to an integer power:
\({\left( {\frac{{\cos \theta – i\sin \theta }}{{\cos \theta }}} \right)^n} = \frac{{\cos n\theta – i\sin n\theta }}{{{{\cos }^n}\theta }}\) A1
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = \frac{{2\cos n\theta }}{{{{\cos }^n}\theta }}\) AG
METHOD 2
\({(1 + {\text{i}}\tan \theta )^n} + {(1 – {\text{i}}\tan \theta )^n} = {(1 + {\text{i}}\tan \theta )^n} + {\left( {1 + {\text{i}}\tan ( – \theta )} \right)^n}\) (M1)
\( = \frac{{{{(\cos \theta + i\sin \theta )}^n}}}{{{{\cos }^n}\theta }} + \frac{{{{\left( {\cos ( – \theta ) + i\sin ( – \theta )} \right)}^n}}}{{{{\cos }^n}\theta }}\) M1A1
Note: Award M1 for converting to cosine and sine terms.
use of de Moivre’s theorem (M1)
\( = \frac{1}{{{{\cos }^n}\theta }}\left( {\cos n\theta + {\text{i}}\sin n\theta + \cos ( – n\theta ) + {\text{i}}\sin ( – n\theta )} \right)\) A1
\( = \frac{{2\cos n\theta }}{{{{\cos }^2}\theta }}\;\;\;{\text{as}}\;\;\;\cos ( – n\theta ) = \cos n\theta \;\;\;{\text{and}}\;\;\;\sin ( – n\theta ) = – \sin n\theta \) R1AG
(ii) \({\left( {1 + {\text{i}}\tan \frac{{3\pi }}{8}} \right)^4} + {\left( {1 – {\text{i}}\tan \frac{{3\pi }}{8}} \right)^4} = \frac{{2\cos \left( {4 \times \frac{{3\pi }}{8}} \right)}}{{{{\cos }^4}\frac{{3\pi }}{8}}}\) (A1)
\( = \frac{{2\cos \frac{{3\pi }}{2}}}{{{{\cos }^4}\frac{{3\pi }}{8}}}\) A1
\( = 0\;\;\;{\text{as}}\;\;\;\cos \frac{{3\pi }}{2} = 0\) R1
Note: The above working could involve theta and the solution of \(\cos (4\theta ) = 0\).
so \({\text{i}}\tan \frac{{3\pi }}{8}\) is a root of the equation AG
(iii) either \( – {\text{i}}\tan \frac{{3\pi }}{8}\;\;\;{\text{or}}\;\;\; – {\text{i}}\tan \frac{\pi }{8}\;\;\;{\text{or}}\;\;\;{\text{i}}\tan \frac{\pi }{8}\) A1
Note: Accept \({\text{i}}\tan \frac{{5\pi }}{8}\;\;\;{\text{or}}\;\;\;{\text{i}}\tan \frac{{7\pi }}{8}\).
Accept \( – \left( {1 + \sqrt 2 } \right){\text{i}}\;\;\;{\text{or}}\;\;\;\left( {1 – \sqrt 2 } \right){\text{i}}\;\;\;{\text{or}}\;\;\;\left( { – 1 + \sqrt 2 } \right){\text{i}}\).
[10 marks]
(i) \(\tan \frac{\pi }{4} = \frac{{2\tan \frac{\pi }{8}}}{{1 – {{\tan }^2}\frac{\pi }{8}}}\) (M1)
\({\tan ^2}\frac{\pi }{8} + 2\tan \frac{\pi }{8} – 1 = 0\) A1
let \(t = \tan \frac{\pi }{8}\)
attempting to solve \({t^2} + 2t – 1 = 0\;\;\;{\text{for}}\;\;\;t\) M1
\(t = – 1 \pm \sqrt 2 \) A1
\(\frac{\pi }{8}\) is a first quadrant angle and tan is positive in this quadrant, so
\(\tan \frac{\pi }{8} > 0\) R1
\(\tan \frac{\pi }{8} = \sqrt 2 – 1\) AG
(ii) \(\cos 4x = 2{\cos ^2}2x – 1\) A1
\( = 2{\left( {2{{\cos }^2}x – 1} \right)^2} – 1\) M1
\( = 2\left( {4{{\cos }^4}x – 4{{\cos }^2}x + 1} \right) – 1\) A1
\( = 8{\cos ^4}x – 8{\cos ^2}x + 1\) AG
Note: Accept equivalent complex number derivation.
(iii) \(\int_0^{\frac{\pi }{8}} {\frac{{2\cos 4x}}{{{{\cos }^2}x}}{\text{d}}x = 2} \int_0^{\frac{\pi }{8}} {\frac{{8{{\cos }^4}x – 8{{\cos }^2}x + 1}}{{{{\cos }^2}x}}{\text{d}}x} \)
\( = 2\int_0^{\frac{\pi }{8}} {8{{\cos }^2}x – 8 + {{\sec }^2}x{\text{d}}x} \) M1
Note: The M1 is for an integrand involving no fractions.
use of \({\cos ^2}x = \frac{1}{2}(\cos 2x + 1)\) M1
\( = 2\int_0^{\frac{\pi }{8}} {4\cos 2x – 4 + {{\sec }^2}x{\text{d}}x} \) A1
\( = [4\sin 2x – 8x + 2\tan x]_0^{\frac{\pi }{8}}\) A1
\( = 4\sqrt 2 – \pi – 2\;\;\;\)(or equivalent) A1
[13 marks]
Total [23 marks]
Examiners report
Fairly successful.
(i) Most candidates attempted to use the hint. Those who doubled the angle were usually successful – but many lost the final mark by not giving a convincing reason to reject the negative solution to the intermediate quadratic equation. Those who halved the angle got nowhere.
(ii) The majority of candidates obtained full marks.
(iii) This was poorly answered, few candidates realising that part of the integrand could be re-expressed using \(\frac{1}{{{{\cos }^2}x}} = {\sec ^2}x\), which can be immediately integrated.
| Marks available | 7 |
| Reference code | 15N.1.hl.TZ0.9 |
Question
Solve the equation \(\sin 2x – \cos 2x = 1 + \sin x – \cos x\) for \(x \in [ – \pi ,{\text{ }}\pi ]\).
Markscheme
\((\sin 2x – \sin x) – (\cos 2x – \cos x) = 1\)
attempt to use both double-angle formulae, in whatever form M1
\((2\sin x\cos x – \sin x) – (2{\cos ^2}x – 1 – \cos x) = 1\)
or \((2\sin x\cos x – \sin x) – (2{\cos ^2}x – \cos x) = 0\) for example A1
Note: Allow any rearrangement of the above equations.
\(\sin x(2\cos x – 1) – \cos x(2\cos x – 1) = 0\)
\((\sin x – \cos x)(2\cos x – 1) = 0\) (M1)
\(\tan x = 1{\text{ and }}\cos x = \frac{1}{2}\) A1A1
Note: These A marks are dependent on the M mark awarded for factorisation.
\(x = – \frac{{3\pi }}{4},{\text{ }} – \frac{\pi }{3},{\text{ }}\frac{\pi }{3},{\text{ }}\frac{\pi }{4}\) A2
Note: Award A1 for two correct answers, which could be for both tan or both cos solutions, for example.
[7 marks]
Examiners report
| Marks available | 3 |
| Reference code | 16M.1.hl.TZ1.5 |
Question
The following diagram shows the triangle ABC where \({\text{AB}} = 2,{\text{ AC}} = \sqrt 2 \) and \({\rm{B\hat AC}} = 15^\circ \).
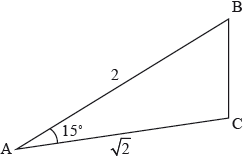
Expand and simplify \({\left( {1 – \sqrt 3 } \right)^2}\).
By writing \(15^\circ \) as \(60^\circ – 45^\circ \) find the value of \(\cos (15^\circ )\).
Find BC in the form \(a + \sqrt b \) where \(a,{\text{ }}b \in \mathbb{Z}\).
Markscheme
\({\left( {1 – \sqrt 3 } \right)^2} = 4 – 2\sqrt 3 \) A1
Note: Award A0 for \(1 – 2\sqrt 3 + 3\).
[1 mark]
\(\cos (60^\circ – 45^\circ ) = \cos (60^\circ )\cos (45^\circ ) + \sin (60^\circ )\sin (45^\circ )\) M1
\( = \frac{1}{2} \times \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 2 }}{2}{\text{ }}\left( {{\text{or }}\frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}} \right)\) (A1)
\( = \frac{{\sqrt 2 + \sqrt 6 }}{4}{\text{ }}\left( {{\text{or }}\frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}} \right)\) A1
[3 marks]
\(B{C^2} = 2 + 4 – 2 \times \sqrt 2 \times 2\cos (15^\circ )\) M1
\( = 6 – \sqrt 2 \left( {\sqrt 2 + \sqrt 6 } \right)\)
\( = 4 – \sqrt {12} {\text{ }}\left( { = 4 – 2\sqrt 3 } \right)\) A1
\(BC = \pm \left( {1 – \sqrt 3 } \right)\) (M1)
\(BC = – 1 + \sqrt 3 \) A1
Note: Accept \(BC = \sqrt 3 – 1\).
Note: Award M1A0 for \(1 – \sqrt 3 \).
Note: Valid geometrical methods may be seen.
[4 marks]
Examiners report
The main error here was to fail to note the word ‘simplify’ in the question and some candidates wrote \(1 + 3\) in their final answer rather than 4.
This was well done by the majority of candidates, though a few wrote \(\cos (60 – 45) = \cos 60 – \cos 45\).
Candidates were able to use the cosine rule correctly but then failed to notice the result obtained was the same as that obtained in part (a).
| Marks available | 2 |
| Reference code | 16N.1.hl.TZ0.13 |
Question
Find the value of \(\sin \frac{\pi }{4} + \sin \frac{{3\pi }}{4} + \sin \frac{{5\pi }}{4} + \sin \frac{{7\pi }}{4} + \sin \frac{{9\pi }}{4}\).
Show that \(\frac{{1 – \cos 2x}}{{2\sin x}} \equiv \sin x,{\text{ }}x \ne k\pi \) where \(k \in \mathbb{Z}\).
Use the principle of mathematical induction to prove that
\(\sin x + \sin 3x + \ldots + \sin (2n – 1)x = \frac{{1 – \cos 2nx}}{{2\sin x}},{\text{ }}n \in {\mathbb{Z}^ + },{\text{ }}x \ne k\pi \) where \(k \in \mathbb{Z}\).
Hence or otherwise solve the equation \(\sin x + \sin 3x = \cos x\) in the interval \(0 < x < \pi \).
Markscheme
\(\sin \frac{\pi }{4} + \sin \frac{{3\pi }}{4} + \sin \frac{{5\pi }}{4} + \sin \frac{{7\pi }}{4} + \sin \frac{{9\pi }}{4} = \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2} – \frac{{\sqrt 2 }}{2} – \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}\) (M1)A1
Note: Award M1 for 5 equal terms with \) + \) or \( – \) signs.
[2 marks]
\(\frac{{1 – \cos 2x}}{{2\sin x}} \equiv \frac{{1 – (1 – 2{{\sin }^2}x)}}{{2\sin x}}\) M1
\( \equiv \frac{{2{{\sin }^2}x}}{{2\sin x}}\) A1
\( \equiv \sin x\) AG
[2 marks]
let \({\text{P}}(n):\sin x + \sin 3x + \ldots + \sin (2n – 1)x \equiv \frac{{1 – \cos 2nx}}{{2\sin x}}\)
if \(n = 1\)
\({\text{P}}(1):\frac{{1 – \cos 2x}}{{2\sin x}} \equiv \sin x\) which is true (as proved in part (b)) R1
assume \({\text{P}}(k)\) true, \(\sin x + \sin 3x + \ldots + \sin (2k – 1)x \equiv \frac{{1 – \cos 2kx}}{{2\sin x}}\) M1
Notes: Only award M1 if the words “assume” and “true” appear. Do not award M1 for “let \(n = k\)” only. Subsequent marks are independent of this M1.
consider \({\text{P}}(k + 1)\):
\({\text{P}}(k + 1):\sin x + \sin 3x + \ldots + \sin (2k – 1)x + \sin (2k + 1)x \equiv \frac{{1 – \cos 2(k + 1)x}}{{2\sin x}}\)
\(LHS = \sin x + \sin 3x + \ldots + \sin (2k – 1)x + \sin (2k + 1)x\) M1
\( \equiv \frac{{1 – \cos 2kx}}{{2\sin x}} + \sin (2k + 1)x\) A1
\( \equiv \frac{{1 – \cos 2kx + 2\sin x\sin (2k + 1)x}}{{2\sin x}}\)
\( \equiv \frac{{1 – \cos 2kx + 2\sin x\cos x\sin 2kx + 2{{\sin }^2}x\cos 2kx}}{{2\sin x}}\) M1
\( \equiv \frac{{1 – \left( {(1 – 2{{\sin }^2}x)\cos 2kx – \sin 2x\sin 2kx} \right)}}{{2\sin x}}\) M1
\( \equiv \frac{{1 – (\cos 2x\cos 2kx – \sin 2x\sin 2kx)}}{{2\sin x}}\) A1
\( \equiv \frac{{1 – \cos (2kx + 2x)}}{{2\sin x}}\) A1
\( \equiv \frac{{1 – \cos 2(k + 1)x}}{{2\sin x}}\)
so if true for \(n = k\) , then also true for \(n = k + 1\)
as true for \(n = 1\) then true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: Accept answers using transformation formula for product of sines if steps are shown clearly.
Note: Award R1 only if candidate is awarded at least 5 marks in the previous steps.
[9 marks]
EITHER
\(\sin x + \sin 3x = \cos x \Rightarrow \frac{{1 – \cos 4x}}{{2\sin x}} = \cos x\) M1
\( \Rightarrow 1 – \cos 4x = 2\sin x\cos x,{\text{ }}(\sin x \ne 0)\) A1
\( \Rightarrow 1 – (1 – 2{\sin ^2}2x) = \sin 2x\) M1
\( \Rightarrow \sin 2x(2\sin 2x – 1) = 0\) M1
\( \Rightarrow \sin 2x = 0\) or \(\sin 2x = \frac{1}{2}\) A1
\(2x = \pi ,{\text{ }}2x = \frac{\pi }{6}\) and \(2x = \frac{{5\pi }}{6}\)
OR
\(\sin x + \sin 3x = \cos x \Rightarrow 2\sin 2x\cos x = \cos x\) M1A1
\( \Rightarrow (2\sin 2x – 1)\cos x = 0,{\text{ }}(\sin x \ne 0)\) M1A1
\( \Rightarrow \sin 2x = \frac{1}{2}\) of \(\cos x = 0\) A1
\(2x = \frac{\pi }{6},{\text{ }}2x = \frac{{5\pi }}{6}\) and \(x = \frac{\pi }{2}\)
THEN
\(\therefore x = \frac{\pi }{2},{\text{ }}x = \frac{\pi }{{12}}\) and \(x = \frac{{5\pi }}{{12}}\) A1
Note: Do not award the final A1 if extra solutions are seen.
[6 marks]
Examiners report
| Marks available | 2 |
| Reference code | SPNone.1.hl.TZ0.1 |
Question
The angle \(\theta \) lies in the first quadrant and \(\cos \theta = \frac{1}{3}\).
Write down the value of \(\sin \theta \) .
Find the value of \(\tan 2\theta \) .
Find the value of \(\cos \left( {\frac{\theta }{2}} \right)\) , giving your answer in the form \(\frac{{\sqrt a }}{b}\) where a , \(b \in {\mathbb{Z}^ + }\) .
Markscheme
\(\sin \theta = \frac{{\sqrt 8 }}{3}\) A1
[1 mark]
\(\tan 2\theta = \frac{{2 \times \sqrt 8 }}{{1 – 8}} = – \frac{{2\sqrt 8 }}{7}\,\,\,\,\,\left( { – \frac{{4\sqrt 2 }}{7}} \right)\) M1A1
[2 marks]
\({\cos ^2}\left( {\frac{\theta }{2}} \right) = \frac{{1 + \frac{1}{3}}}{2} = \frac{2}{3}\) M1A1
\(\cos \left( {\frac{\theta }{2}} \right) = \frac{{\sqrt 6 }}{3}\) A1
[3 marks]
Examiners report
| Marks available | 3 |
| Reference code | SPNone.1.hl.TZ0.1 |
Question
The angle \(\theta \) lies in the first quadrant and \(\cos \theta = \frac{1}{3}\).
Write down the value of \(\sin \theta \) .
Find the value of \(\tan 2\theta \) .
Find the value of \(\cos \left( {\frac{\theta }{2}} \right)\) , giving your answer in the form \(\frac{{\sqrt a }}{b}\) where a , \(b \in {\mathbb{Z}^ + }\) .
Markscheme
\(\sin \theta = \frac{{\sqrt 8 }}{3}\) A1
[1 mark]
\(\tan 2\theta = \frac{{2 \times \sqrt 8 }}{{1 – 8}} = – \frac{{2\sqrt 8 }}{7}\,\,\,\,\,\left( { – \frac{{4\sqrt 2 }}{7}} \right)\) M1A1
[2 marks]
\({\cos ^2}\left( {\frac{\theta }{2}} \right) = \frac{{1 + \frac{1}{3}}}{2} = \frac{2}{3}\) M1A1
\(\cos \left( {\frac{\theta }{2}} \right) = \frac{{\sqrt 6 }}{3}\) A1
[3 marks]