Question: [Maximum mark: 6]
The following diagram shows a circle with centre O and radius 5 metres.
Points A and B lie on the circle and \(A\hat{O}B\) = 1.9 radians.
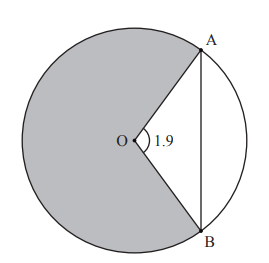
(a) Find the length of the chord [AB].
(b) Find the area of the shaded sector.
▶️Answer/Explanation
Ans:
(a) EITHER
uses the cosine rule
AB2 = 52 + 52 -2 × 5 × 5 × cos1.9
OR
uses right-angled trigonometry
\(\frac{\frac{AB}{2}}{5}= sin 0.95\)
OR
uses the sine rule
\(\alpha \frac{1}{2}(\pi -1.9)(=0.6207…)\)
\(\frac{AB}{sin1.9}= \frac{5}{sin0.6207….}\)
THEN
AB = 8.1341…
AB = 8.13 (m)
(b) let the shaded area be A
METHOD 1
Attempt at finding reflex angle
\(A\hat{O}B = 2\pi -1.9 (=4.3831….)\)
substitution into area formula
\(A = \frac{1}{2}\times 5^{2}\times 4.3831…. OR \left ( \frac{2\pi -1.9}{2\pi } \right )\times \pi \left ( 5^{2} \right )\)
= 54.7898…
= 54.8 (m2)
METHOD 2
let the area of the circle be AC and the area of the unshaded sector be AU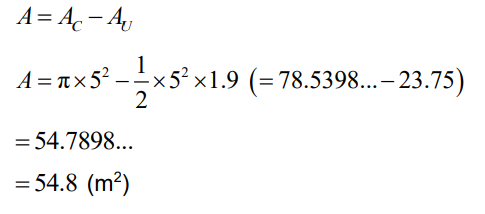
Question
In triangle ABC, BC = a , AC = b , AB = c and [BD] is perpendicular to [AC].
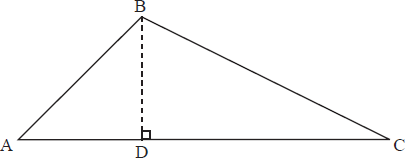
(a) Show that \({\text{CD}} = b – c\cos A\).
(b) Hence, by using Pythagoras’ Theorem in the triangle BCD, prove the cosine rule for the triangle ABC.
(c) If \({\rm{A\hat BC}} = 60^\circ \) , use the cosine rule to show that \(c = \frac{1}{2}a \pm \sqrt {{b^2} – \frac{3}{4}{a^2}} \) .[12]
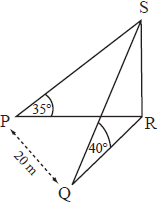
The above three dimensional diagram shows the points P and Q which are respectively west and south-west of the base R of a vertical flagpole RS on horizontal ground. The angles of elevation of the top S of the flagpole from P and Q are respectively 25° and 40° , and PQ = 20 m .
Determine the height of the flagpole.[8]
▶️Answer/Explanation
Markscheme
(a) \({\text{CD}} = {\text{AC}} – {\text{AD}} = b – c\cos A\) R1AG
[1 mark]
(b) METHOD 1
\({\text{B}}{{\text{C}}^2} = {\text{B}}{{\text{D}}^2} + {\text{C}}{{\text{D}}^2}\) (M1)
\({a^2} = {(c\sin A)^2} + {(b – c\cos A)^2}\) (A1)
\( = {c^2}{\sin ^2}A + {b^2} – 2bc\cos A + {c^2}{\cos ^2}A\) A1
\( = {b^2} + {c^2} – 2bc\cos A\) A1
[4 marks]
METHOD 2
\({\text{B}}{{\text{D}}^2} = {\text{A}}{{\text{B}}^2} – {\text{A}}{{\text{D}}^2} = {\text{B}}{{\text{C}}^2} – {\text{C}}{{\text{D}}^2}\) (M1)(A1)
\( \Rightarrow {c^2} – {c^2}{\cos ^2}A = {a^2} – {b^2} + 2bc\cos A – {c^2}{\cos ^2}A\) A1
\( \Rightarrow {a^2} = {b^2} + {c^2} – 2bc\cos A\) A1
[4 marks]
(c) METHOD 1
\({b^2} = {a^2} + {c^2} – 2ac\cos 60^\circ \Rightarrow {b^2} = {a^2} + {c^2} – ac\) (M1)A1
\( \Rightarrow {c^2} – ac + {a^2} – {b^2} = 0\) M1
\( \Rightarrow c = \frac{{a \pm \sqrt {{{( – a)}^2} – 4({a^2} – {b^2})} }}{2}\) (M1)A1
\( = \frac{{a \pm \sqrt {4{b^2} – 3{a^2}} }}{2} = \frac{a}{2} \pm \sqrt {\frac{{4{b^2} – 3{a^2}}}{4}} \) (M1)A1
\( = \frac{1}{2}a \pm \sqrt {{b^2} – \frac{3}{4}{a^2}} \) AG
Note: Candidates can only obtain a maximum of the first three marks if they verify that the answer given in the question satisfies the equation.
[7 marks]
METHOD 2
\({b^2} = {a^2} + {c^2} – 2ac\cos 60^\circ \Rightarrow {b^2} = {a^2} + {c^2} – ac\) (M1)A1
\({c^2} – ac = {b^2} – {a^2}\) (M1)
\({c^2} – ac + {\left( {\frac{a}{2}} \right)^2} = {b^2} – {a^2} + {\left( {\frac{a}{2}} \right)^2}\) M1A1
\({\left( {c – \frac{a}{2}} \right)^2} = {b^2} – \frac{3}{4}{a^2}\) (A1)
\(c – \frac{a}{2} = \pm \sqrt {{b^2} – \frac{3}{4}{a^2}} \) A1
\( \Rightarrow c = \frac{1}{2}a \pm \sqrt {{b^2} – \frac{3}{4}{a^2}} \) AG
[7 marks]
\({\text{PR}} = h\tan 55^\circ {\text{ , QR}} = h\tan 50^\circ {\text{ where RS}} = h\) M1A1A1
Use the cosine rule in triangle PQR. (M1)
\({20^2} = {h^2}{\tan ^2}55^\circ + {h^2}{\tan ^2}50^\circ – 2h\tan 55^\circ h\tan 50^\circ \cos 45^\circ \) A1
\({h^2} = \frac{{400}}{{{{\tan }^2}55^\circ + {{\tan }^2}50^\circ – 2\tan 55^\circ \tan 50^\circ \cos 45^\circ }}\) (A1)
\( = 379.9…\) (A1)
\(h = 19.5{\text{ (m)}}\) A1
[8 marks]
Question
In the right circular cone below, O is the centre of the base which has radius 6 cm. The points B and C are on the circumference of the base of the cone. The height AO of the cone is 8 cm and the angle \({\rm{B\hat OC}}\) is 60°.
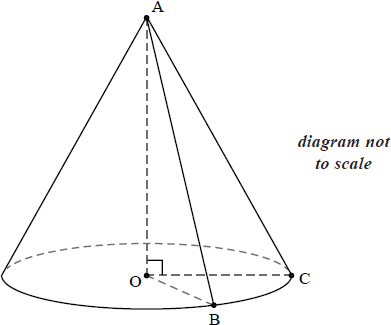
Calculate the size of the angle \({\rm{B\hat AC}}\).
▶️Answer/Explanation
Markscheme
AC = AB = 10 (cm) A1
triangle OBC is equilateral (M1)
BC = 6 (cm) A1
EITHER
\({\rm{B\hat AC}} = 2\arcsin \frac{3}{{10}}\) M1A1
\({\rm{B\hat AC}} = 34.9^\circ \,\,\,\,\,\)(accept 0.609 radians) A1
OR
\(\cos {\rm{B\hat AC = }}\frac{{{{10}^2} + {{10}^2} – {6^2}}}{{2 \times 10 \times 10}} = \frac{{164}}{{200}}\) M1A1
\({\rm{B\hat AC}} = 34.9^\circ \,\,\,\,\,\)(accept 0.609 radians) A1
Note: Other valid methods may be seen.
[6 marks]
Question
Consider the triangle ABC where \({\rm{B\hat AC}} = 70^\circ \), AB = 8 cm and AC = 7 cm. The point D on the side BC is such that \(\frac{{{\text{BD}}}}{{{\text{DC}}}} = 2\).
Determine the length of AD.
▶️Answer/Explanation
Markscheme
use of cosine rule: \({\text{BC}} = \sqrt {({8^2} + {7^2} – 2 \times 7 \times 8\cos 70)} = 8.6426 \ldots \) (M1)A1
Note: Accept an expression for \({\text{B}}{{\text{C}}^2}\).
\({\text{BD}} = 5.7617 \ldots \,\,\,\,\,{\text{(CD}} = 2.88085 \ldots )\) A1
use of sine rule: \(\hat B = \arcsin \left( {\frac{{7\sin 70}}{{{\text{BC}}}}} \right) = 49.561 \ldots ^\circ \,\,\,\,\,(\hat C = 60.4387 \ldots ^\circ )\) (M1)A1
use of cosine rule: \({\text{AD}} = \sqrt {{8^2} + {\text{B}}{{\text{D}}^2} – 2 \times {\text{BD}} \times 8\cos B} = 6.12{\text{ (cm)}}\) A1
Note: Scale drawing method not acceptable.
[6 marks]
Question
Given \(\Delta \)ABC, with lengths shown in the diagram below, find the length of the line segment [CD].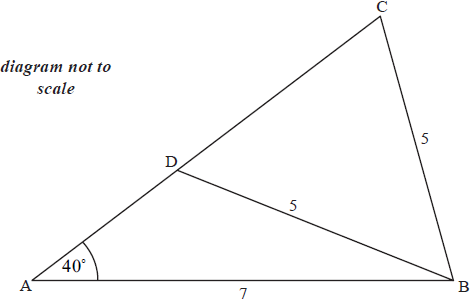
▶️Answer/Explanation
Markscheme
METHOD 1
\(\frac{{\sin C}}{7} = \frac{{\sin 40}}{5}\) M1(A1)
\({\text{B}}\hat {\text{C}}{\text{D}} = 64.14…^\circ \) A1
\({\text{CD}} = 2 \times 5\cos 64.14…\) M1
Note: Also allow use of sine or cosine rule.
\({\text{CD}} = 4.36\) A1
[5 marks]
METHOD 2
let \({\text{AC}} = x\)
cosine rule
\({5^2} = {7^2} + {x^2} – 2 \times 7 \times x\cos 40\) M1A1
\({x^2} – 10.7 … x + 24 = 0\)
\(x = \frac{{10.7… \pm \sqrt {{{\left( {10.7…} \right)}^2} – 4 \times 24} }}{2}\) (M1)
\(x = 7.54\); \(3.18\) (A1)
CD is the difference in these two values \(= 4.36\) A1
Note: Other methods may be seen.
[5 marks
Question
An electricity station is on the edge of a straight coastline. A lighthouse is located in the sea 200 m from the electricity station. The angle between the coastline and the line joining the lighthouse with the electricity station is 60°. A cable needs to be laid connecting the lighthouse to the electricity station. It is decided to lay the cable in a straight line to the coast and then along the coast to the electricity station. The length of cable laid along the coastline is x metres. This information is illustrated in the diagram below.
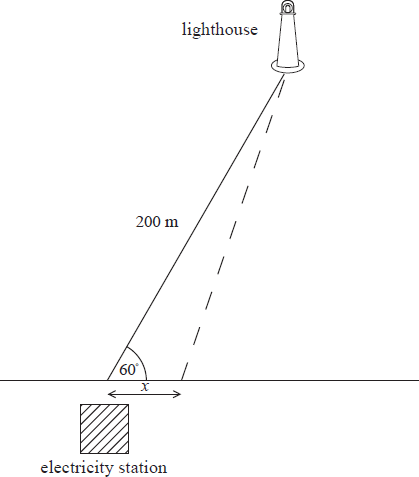
The cost of laying the cable along the sea bed is US$80 per metre, and the cost of laying it on land is US$20 per metre.
a.Find, in terms of x, an expression for the cost of laying the cable.[4]
b.Find the value of x, to the nearest metre, such that this cost is minimized.[2]
▶️Answer/Explanation
Markscheme
let the distance the cable is laid along the seabed be y
\({y^2} = {x^2} + {200^2} – 2 \times x \times 200\cos 60^\circ \) (M1)
(or equivalent method)
\({y^2} = {x^2} – 200x + 40000\) (A1)
cost = C = 80y + 20x (M1)
\(C = 80{({x^2} – 200x + 40000)^{\frac{1}{2}}} + 20x\) A1
[4 marks]
\(x = 55.2786 \ldots = 55\) (m to the nearest metre) (A1)A1
\(\left( {x = 100 – \sqrt {2000} } \right)\)
[2 marks]