Question
In the diagram below, [AB] is a diameter of the circle with centre O. Point C is on the circumference of the circle. Let \(\overrightarrow {{\text{OB}}} = \boldsymbol{b} \) and \(\overrightarrow {{\text{OC}}} = \boldsymbol{c}\) .
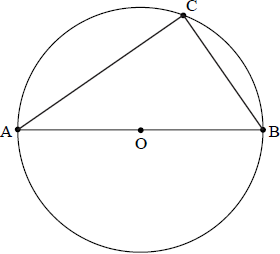
a. Find an expression for \(\overrightarrow {{\text{CB}}} \) and for \(\overrightarrow {{\text{AC}}} \) in terms of \(\boldsymbol{b}\) and \(\boldsymbol{c}\) . [2]
b. Hence prove that \({\rm{A\hat CB}}\) is a right angle.[3]
▶️Answer/Explanation
Markscheme
a.
\(\overrightarrow {{\text{CB}}} = \boldsymbol{b} – \boldsymbol{c}\) , \(\overrightarrow {{\text{AC}}} = \boldsymbol{b} + \boldsymbol{c}\) A1A1
Note: Condone absence of vector notation in (a).
[2 marks]
\(\overrightarrow {{\text{AC}}} \cdot \overrightarrow {{\text{CB}}} = \)(b + c)\( \cdot \)(b – c) M1
= \(|\)b\({|^2}\) – \(|\)c\({|^2}\) A1
= 0 since \(|\)b\(|\) = \(|\)c\(|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AC}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\rm{A\hat CB}}\) is a right angle AG [3 marks]
Question
a. Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square. [3]
b.Find the coordinates of M, the mid-point of [OB]. [1]
c.Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
d. Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]e. Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
f. Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
(ii) State what this tells you about the solid OABCDE. [6]
▶️Answer/Explanation
Markscheme
a.
\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
[
Question
a. Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square.[3]
b.Find the coordinates of M, the mid-point of [OB].[1]
c.Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
d. Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]
e. Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
f.Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
(ii) State what this tells you about the solid OABCDE. [6]
▶️Answer/Explanation
Markscheme
a.
\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
Question
PQRS is a rhombus. Given that \(\overrightarrow {{\text{PQ}}} = \) \(\boldsymbol{a}\) and \(\overrightarrow {{\text{QR}}} = \) \(\boldsymbol{b}\),
(a) express the vectors \(\overrightarrow {{\text{PR}}} \) and \(\overrightarrow {{\text{QS}}} \) in terms of \(\boldsymbol{a}\) and \(\boldsymbol{b}\);
(b) hence show that the diagonals in a rhombus intersect at right angles.
▶️Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{PR}}} = \) a + b A1
\(\overrightarrow {{\text{QS}}} = \) b − a A1
[2 marks]
(b) \(\overrightarrow {{\text{PR}}} \cdot \overrightarrow {{\text{QS}}} = \) (a + b) \( \cdot \) (b − a) M1
\( = |\)b\({|^2} – |\)a\({|^2}\) A1
for a rhombus \(|\)a\(| = |\)b\(|\) R1
hence \(|\)b\({|^2} – |\)a\({|^2} = 0\) A1
Note: Do not award the final A1 unless R1 is awarded.
hence the diagonals intersect at right angles AG
[4 marks]Total [6 marks]
Question
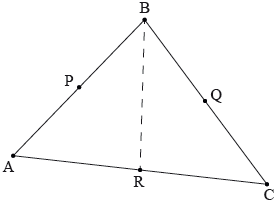
Consider the triangle \(ABC\). The points \(P\), \(Q\) and \(R\) are the midpoints of the line segments [\(AB\)], [\(BC\)] and [\(AC\)] respectively.
Let \(\overrightarrow {{\text{OA}}} = {{a}}\), \(\overrightarrow {{\text{OB}}} = {{b}}\) and \(\overrightarrow {{\text{OC}}} = {{c}}\).
a. Find \(\overrightarrow {{\text{BR}}} \) in terms of \({{a}}\), \({{b}}\) and \({{c}}\).[2]
(ii) Find a vector equation of the line that passes through \(A\) and \(Q\) in terms of \({{a}}\), \({{b}}\) and \({{c}}\) and a parameter \(\mu \).
(iii) Hence show that \(\overrightarrow {{\text{OG}}} = \frac{1}{3}({{a}} + {{b}} + {{c}})\) given that \(G\) is the point where [\(BR\)] and [\(AQ\)] intersect.[9]
c.Show that the line segment [\(CP\)] also includes the point \(G\).[3]
d.The coordinates of the points \(A\), \(B\) and \(C\) are \((1,{\text{ }}3,{\text{ }}1)\), \((3,{\text{ }}7,{\text{ }} – 5)\) and \((2,{\text{ }}2,{\text{ }}1)\) respectively.
A point \(X\) is such that [\(GX\)] is perpendicular to the plane \(ABC\).
▶️Answer/Explanation
Markscheme
a.\(\overrightarrow {{\text{BR}}} = \overrightarrow {{\text{BA}}} + \overrightarrow {{\text{AR}}} \;\;\;\left( { = \overrightarrow {{\text{BA}}} + \frac{1}{2}\overrightarrow {{\text{AC}}} } \right)\) (M1)
\( = ({{a}} – {{b}}) + \frac{1}{2}({{c}} – {{a}})\)
\( = \frac{1}{2}{{a}} – {{b}} + \frac{1}{2}{{c}}\) A1
[2 marks]
(i) \({{\text{r}}_{{\text{BR}}}} = {{b}} + \lambda \left( {\frac{1}{2}{{a}} – {{b}} + \frac{1}{2}{{c}}} \right)\;\;\;\left( { = \frac{\lambda }{2}{{a}} + (1 – \lambda ){{b}} + \frac{\lambda }{2}{{c}}} \right)\) A1A1
Note: Award A1A0 if the \({\text{r}} = \) is omitted in an otherwise correct expression/equation.
Do not penalise such an omission more than once.
(ii) \(\overrightarrow {{\text{AQ}}} = – {{a}} + \frac{1}{2}{{b}} + \frac{1}{2}{{c}}\) (A1)
\({{\text{r}}_{{\text{AQ}}}} = {{a}} + \mu \left( { – {{a}} + \frac{1}{2}{{b}} + \frac{1}{2}{{c}}} \right)\;\;\;\left( { = (1 – \mu ){{a}} + \frac{\mu }{2}{{b}} + \frac{\mu }{2}{{c}}} \right)\) A1
Note: Accept the use of the same parameter in (i) and (ii).
(iii) when \(\overrightarrow {{\text{AQ}}} \) and \(\overrightarrow {{\text{BP}}} \) intersect we will have \({{\text{r}}_{{\text{BR}}}} = {{\text{r}}_{{\text{AQ}}}}\) (M1)
Note: If the same parameters are used for both equations, award at most M1M1A0A0M1.
\(\frac{\lambda }{2}{{a}} + (1 – \lambda ){{b}} + \frac{\lambda }{2}{{c}} = (1 – \mu ){{a}} + \frac{\mu }{2}{{b}} + \frac{\mu }{2}{{c}}\)
attempt to equate the coefficients of the vectors \({{a}}\), \({{b}}\) and \({{c}}\) M1
\(\left. {\begin{array}{*{20}{c}} {\frac{\lambda }{2} = 1 – \mu } \\ {1 – \lambda = \frac{\mu }{2}} \\ {\frac{\lambda }{2} = \frac{\mu }{2}} \end{array}} \right\}\) (A1)
\(\lambda = \frac{2}{3}\) or \(\mu = \frac{2}{3}\) A1
substituting parameters back into one of the equations M1
\(\overrightarrow {{\text{OG}}} = \frac{1}{2} \bullet \frac{2}{3}{{a}} + \left( {1 – \frac{2}{3}} \right){{b}} + \frac{1}{2} \bullet \frac{2}{3}{{c}} = \frac{1}{3}({{a}} + {{b}} + {{c}})\) AG
Note: Accept solution by verification.
[9 marks]
\(\overrightarrow {{\text{CP}}} = \frac{1}{2}{{a}} + \frac{1}{2}{{b}} – {{c}}\) (M1)A1
so we have that \({{\text{r}}_{{\text{CP}}}} = {{c}} + \beta \left( {\frac{1}{2}{{a}} + \frac{1}{2}{{b}} – {{c}}} \right)\) and when \(\beta = \frac{2}{3}\) the line passes through
the point \(G\) (ie, with position vector \(\frac{1}{3}({{a}} + {{b}} + {{c}})\)) R1
hence [\(AQ\)], [\(BR\)] and [\(CP\)] all intersect in \(G\) AG
[3 marks]
\(\overrightarrow {{\text{OG}}} = \frac{1}{3}\left( {\left( {\begin{array}{*{20}{c}} 1 \\ 3 \\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 3 \\ 7 \\ { – 5} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2 \\ 2 \\ 1 \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 1} \end{array}} \right)\) A1
Note: This independent mark for the vector may be awarded wherever the vector is calculated.
\(\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} = \left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 6} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ 0 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 6} \\ { – 6} \\ { – 6} \end{array}} \right)\) M1A1
\(\overrightarrow {{\text{GX}}} = \alpha \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)\) (M1)
volume of Tetrahedron given by \(\frac{1}{3} \times {\text{Area ABC}} \times {\text{GX}}\)
\( = \frac{1}{3}\left( {\frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|} \right) \times {\text{GX}} = 12\) (M1)(A1)
Note: Accept alternative methods, for example the use of a scalar triple product.
\( = \frac{1}{6}\sqrt {{{( – 6)}^2} + {{( – 6)}^2} + {{( – 6)}^2}} \times \sqrt {{\alpha ^2} + {\alpha ^2} + {\alpha ^2}} = 12\) (A1)
\( = \frac{1}{6}6\sqrt 3 |\alpha |\sqrt 3 = 12\)
\( \Rightarrow |\alpha | = 4\) A1
Note: Condone absence of absolute value.
this gives us the position of \(X\) as \(\left( {\begin{array}{*{20}{c}} 2 \\ 4 \\ { – 1} \end{array}} \right) \pm \left( {\begin{array}{*{20}{c}} 4 \\ 4 \\ 4 \end{array}} \right)\)
\({\text{X}}(6,{\text{ }}8,{\text{ }}3)\) or \(( – 2,{\text{ }}0,{\text{ }} – 5)\) A1
Note: Award A1 for either result.
[9 marks]
Total [23 marks]
Question
O, A, B and C are distinct points such that \(\overrightarrow {{\text{OA}}} = \) a, \(\overrightarrow {{\text{OB}}} = \) b and \(\overrightarrow {{\text{OC}}} = \) c.
It is given that c is perpendicular to \(\overrightarrow {{\text{AB}}} \) and b is perpendicular to \(\overrightarrow {{\text{AC}}} \).
Prove that a is perpendicular to \(\overrightarrow {{\text{BC}}} \).
▶️Answer/Explanation
Markscheme
c \( \bullet \) (b \( – \) a) \( = 0\) M1
Note: Allow c \( \bullet \) \(\overrightarrow {{\text{AB}}} = 0\) or similar for M1.
c \( \bullet \) b \( = \) c \( \bullet \) a A1
b \( \bullet \) (c \( – \) a) \( = 0\)
b \( \bullet \) c \( = \) b \( \bullet \) a A1
c \( \bullet \) a \( = \) b \( \bullet \) a M1
(c \( – \) b) \( \bullet \) a \( = 0\) A1
hence a is perpendicular to \(\overrightarrow {{\text{BC}}} \) AG
Note: Only award the final A1 if a dot is used throughout to indicate scalar product.
Condone any lack of specific indication that the letters represent vectors.
[5 marks]
Question
In the following diagram, \(\overrightarrow {{\text{OA}}} \) = a, \(\overrightarrow {{\text{OB}}} \) = b. C is the midpoint of [OA] and \(\overrightarrow {{\text{OF}}} = \frac{1}{6}\overrightarrow {{\text{FB}}} \).
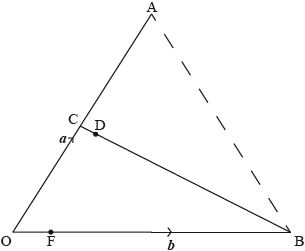
It is given also that \(\overrightarrow {{\text{AD}}} = \lambda \overrightarrow {{\text{AF}}} \) and \(\overrightarrow {{\text{CD}}} = \mu \overrightarrow {{\text{CB}}} \), where \(\lambda ,{\text{ }}\mu \in \mathbb{R}\).
a.i.Find, in terms of a and b \(\overrightarrow {{\text{OF}}} \).[1]
a.ii.Find, in terms of a and b \(\overrightarrow {{\text{AF}}} \).[2]
b.ii.Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\mu \).[2]
c.Show that \(\mu = \frac{1}{{13}}\), and find the value of \(\lambda \).[4]
d.Deduce an expression for \(\overrightarrow {{\text{CD}}} \) in terms of a and b only.[2]
e.Given that area \(\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\), find the value of \(k\). [5]
▶️Answer/Explanation
Markscheme
a.i.\(\overrightarrow {{\text{OF}}} = \frac{1}{7}\)b A1
[1 mark]
\(\overrightarrow {{\text{AF}}} = \overrightarrow {{\text{OF}}} – \overrightarrow {{\text{OA}}} \) (M1)
\( = \frac{1}{7}\)b – a A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \) a \( + \lambda \left( {\frac{1}{7}b -a} \right){\text{ }}\left( { = (1 – \lambda )a + \frac{\lambda }{7}b} \right)\) M1A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \frac{1}{2}\) a \( + \mu \left( { – \frac{1}{2}a + b} \right){\text{ }}\left( { = \left( {\frac{1}{2} – \frac{\mu }{2}} \right)a + \mu b} \right)\) M1A1
[2 marks]
equating coefficients: M1
\(\frac{\lambda }{7} = \mu ,{\text{ }}1 – \lambda = \frac{{1 – \mu }}{2}\) A1
solving simultaneously: M1
\(\lambda = \frac{7}{{13}},{\text{ }}\mu = \frac{1}{{13}}\) A1AG
[4 marks]
\(\overrightarrow {{\text{CD}}} = \frac{1}{{13}}\overrightarrow {{\text{CB}}} \)
\( = \frac{1}{{13}}\left( {b – \frac{1}{2}a} \right){\text{ }}\left( { = – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)\) M1A1
[2 marks]
METHOD 1
\({\text{area }}\Delta {\text{ACD}} = \frac{1}{2}{\text{CD}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{area }}\Delta {\text{ACB}} = \frac{1}{2}{\text{CB}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{ratio }}\frac{{{\text{area }}\Delta {\text{ACD}}}}{{{\text{area }}\Delta {\text{ACB}}}} = \frac{{{\text{CD}}}}{{{\text{CB}}}} = \frac{1}{{13}}\) A1
\(k = \frac{{{\text{area }}\Delta {\text{OAB}}}}{{{\text{area }}\Delta {\text{CAD}}}} = \frac{{13}}{{{\text{area }}\Delta {\text{CAB}}}} \times {\text{area }}\Delta {\text{OAB}}\) (M1)
\( = 13 \times 2 = 26\) A1
METHOD 2
\({\text{area }}\Delta {\text{OAB}} = \frac{1}{2}\left| {a \times b} \right|\) A1
\({\text{area }}\Delta {\text{CAD}} = \frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CD}}} } \right|\) or \(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{AD}}} } \right|\) M1
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)} \right|\)
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a} \right) + \frac{1}{2}a \times \frac{1}{{13}}b} \right|\) (M1)
\( = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{{13}}\left| {a \times b} \right|{\text{ }}\left( { = \frac{1}{{52}}\left| {a \times b} \right|} \right)\) A1
\({\text{area }}\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\)
\(\frac{1}{2}\left| {a \times b} \right| = k\frac{1}{{52}}\left| {a \times b} \right|\)
\(k = 26\) A1 [5 marks]
Question
In the following diagram, \(\overrightarrow {{\text{OA}}} \) = a, \(\overrightarrow {{\text{OB}}} \) = b. C is the midpoint of [OA] and \(\overrightarrow {{\text{OF}}} = \frac{1}{6}\overrightarrow {{\text{FB}}} \).

It is given also that \(\overrightarrow {{\text{AD}}} = \lambda \overrightarrow {{\text{AF}}} \) and \(\overrightarrow {{\text{CD}}} = \mu \overrightarrow {{\text{CB}}} \), where \(\lambda ,{\text{ }}\mu \in \mathbb{R}\).
a.i.Find, in terms of a and b \(\overrightarrow {{\text{OF}}} \).[1]
a.ii.Find, in terms of a and b \(\overrightarrow {{\text{AF}}} \).[2]
b.i.Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\lambda \);[2]
b.ii.Find an expression for \(\overrightarrow {{\text{OD}}} \) in terms of a, b and \(\mu \).[2]
c.Show that \(\mu = \frac{1}{{13}}\), and find the value of \(\lambda \).[4]
d.Deduce an expression for \(\overrightarrow {{\text{CD}}} \) in terms of a and b only.[2]
e.Given that area \(\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\), find the value of \(k\). [5]
▶️Answer/Explanation
Markscheme
a.i.\(\overrightarrow {{\text{OF}}} = \frac{1}{7}\)b A1
[1 mark]
\(\overrightarrow {{\text{AF}}} = \overrightarrow {{\text{OF}}} – \overrightarrow {{\text{OA}}} \) (M1)
\( = \frac{1}{7}\)b – a A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \) a \( + \lambda \left( {\frac{1}{7}b -a} \right){\text{ }}\left( { = (1 – \lambda )a + \frac{\lambda }{7}b} \right)\) M1A1
[2 marks]
\(\overrightarrow {{\text{OD}}} = \frac{1}{2}\) a \( + \mu \left( { – \frac{1}{2}a + b} \right){\text{ }}\left( { = \left( {\frac{1}{2} – \frac{\mu }{2}} \right)a + \mu b} \right)\) M1A1
[2 marks]
equating coefficients: M1
\(\frac{\lambda }{7} = \mu ,{\text{ }}1 – \lambda = \frac{{1 – \mu }}{2}\) A1
solving simultaneously: M1
\(\lambda = \frac{7}{{13}},{\text{ }}\mu = \frac{1}{{13}}\) A1AG
[4 marks]
\(\overrightarrow {{\text{CD}}} = \frac{1}{{13}}\overrightarrow {{\text{CB}}} \)
\( = \frac{1}{{13}}\left( {b – \frac{1}{2}a} \right){\text{ }}\left( { = – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)\) M1A1
[2 marks]
METHOD 1
\({\text{area }}\Delta {\text{ACD}} = \frac{1}{2}{\text{CD}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{area }}\Delta {\text{ACB}} = \frac{1}{2}{\text{CB}} \times {\text{AC}} \times \sin {\rm{A\hat CB}}\) (M1)
\({\text{ratio }}\frac{{{\text{area }}\Delta {\text{ACD}}}}{{{\text{area }}\Delta {\text{ACB}}}} = \frac{{{\text{CD}}}}{{{\text{CB}}}} = \frac{1}{{13}}\) A1
\(k = \frac{{{\text{area }}\Delta {\text{OAB}}}}{{{\text{area }}\Delta {\text{CAD}}}} = \frac{{13}}{{{\text{area }}\Delta {\text{CAB}}}} \times {\text{area }}\Delta {\text{OAB}}\) (M1)
\( = 13 \times 2 = 26\) A1
METHOD 2
\({\text{area }}\Delta {\text{OAB}} = \frac{1}{2}\left| {a \times b} \right|\) A1
\({\text{area }}\Delta {\text{CAD}} = \frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CD}}} } \right|\) or \(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{AD}}} } \right|\) M1
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a + \frac{1}{{13}}b} \right)} \right|\)
\( = \frac{1}{2}\left| {\frac{1}{2}a \times \left( { – \frac{1}{{26}}a} \right) + \frac{1}{2}a \times \frac{1}{{13}}b} \right|\) (M1)
\( = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{{13}}\left| {a \times b} \right|{\text{ }}\left( { = \frac{1}{{52}}\left| {a \times b} \right|} \right)\) A1
\({\text{area }}\Delta {\text{OAB}} = k({\text{area }}\Delta {\text{CAD}})\)
\(\frac{1}{2}\left| {a \times b} \right| = k\frac{1}{{52}}\left| {a \times b} \right|\)
\(k = 26\) A1
[5 marks]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]
b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ. [2]
▶️Answer/Explanation
Markscheme
a.i.a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1 [4 marks]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ. [2]
▶️Answer/Explanation
Markscheme
a.i.a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen. [4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side. [3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1 [2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1 [4 marks]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ. [2]
▶️Answer/Explanation
Markscheme
a.i.a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen. [4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side. [3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1 [2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1 [4 marks]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]
b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ. [2]
▶️Answer/Explanation
Markscheme
a.i.a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.
[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.
[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1
[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1
[4 marks]
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]
b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii. Find YZ. [2]
▶️Answer/Explanation
Markscheme
a.i.a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.
[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.
[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1
[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1
[4 marks]