Question
Consider the vectors a and b such that \(a = \binom{12}{-5} and |b| = 15\)
(a) Find the possible range of values for | a + b |.
Consider the vector p such that p = a + b.
(b) Given that | a + b | is a minimum, find p.
Consider the vector q such that \(q =\binom{x}{y}\), where x , y ∈ R+ .
(c) Find q such that |q| = |b| and q is perpendicular to a.
▶️Answer/Explanation
Ans:
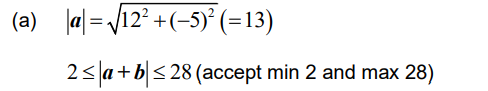
Note: Award (A1)A0 for 2 and 28 seen with no indication that they are the endpoints of an interval.
(b) recognition that p or b is a negative multiple of a
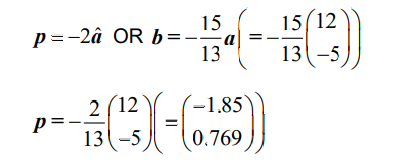
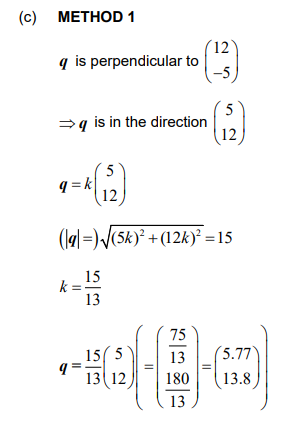
Question
The following diagram shows two perpendicular vectors u and v.
a.Let \(w = u – v\). Represent \(w\) on the diagram above.[2]
b.Given that \(u = \left( \begin{array}{c}3\\2\\1\end{array} \right)\) and \(v = \left( \begin{array}{c}5\\n\\3\end{array} \right)\), where \(n \in \mathbb{Z}\), find \(n\).[4]
▶️Answer/Explanation
Markscheme
METHOD 1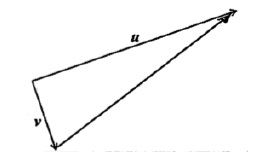
A1A1 N2
Note: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
METHOD 2
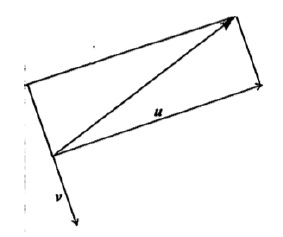A1A1 N2
Notes: Award A1 for segment connecting endpoints and A1 for direction (must see arrow).
Additional lines not required.
[2 marks]
evidence of setting scalar product equal to zero (seen anywhere) R1
eg u \( \cdot \) v \( = 0,{\text{ }}15 + 2n + 3 = 0\)
correct expression for scalar product (A1)
eg \(3 \times 5 + 2 \times n + 1 \times 3,{\text{ }}2n + 18 = 0\)
attempt to solve equation (M1)
eg \(2n = – 18\)
\(n = – 9\) A1 N3
[4 marks]
Question
Two points P and Q have coordinates (3, 2, 5) and (7, 4, 9) respectively.
Let \({\mathop {{\text{PR}}}\limits^ \to }\) = 6i − j + 3k.
a.i.Find \(\mathop {{\text{PQ}}}\limits^ \to \).[2]
a.ii.Find \(\left| {\mathop {{\text{PQ}}}\limits^ \to } \right|\).[2]
b.Find the angle between PQ and PR.[4]
c.Find the area of triangle PQR.[2
d.Hence or otherwise find the shortest distance from R to the line through P and Q.[3]
▶️Answer/Explanation
Markscheme
valid approach (M1)
eg (7, 4, 9) − (3, 2, 5) A − B
\(\mathop {{\text{PQ}}}\limits^ \to = \) 4i + 2j + 4k \(\left( { = \left( \begin{gathered}
4 \hfill \\
2 \hfill \\
4 \hfill \\
\end{gathered} \right)} \right)\) A1 N2
[2 marks]
correct substitution into magnitude formula (A1)
eg \(\sqrt {{4^2} + {2^2} + {4^2}} \)
\(\left| {\mathop {{\text{PQ}}}\limits^ \to } \right| = 6\) A1 N2
[2 marks]
finding scalar product and magnitudes (A1)(A1)
scalar product = (4 × 6) + (2 × (−1) + (4 × 3) (= 34)
magnitude of PR = \(\sqrt {36 + 1 + 9} = \left( {6.782} \right)\)
correct substitution of their values to find cos \({\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}\) M1
eg cos \({\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}\,\,{\text{ = }}\frac{{24 – 2 + 12}}{{\left( 6 \right) \times \left( {\sqrt {46} } \right)}},\,\,0.8355\)
0.581746
\({\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}\) = 0.582 radians or \({\text{Q}}\mathop {\text{P}}\limits^ \wedge {\text{R}}\) = 33.3° A1 N3
[4 marks]
correct substitution (A1)
eg \(\frac{1}{2} \times \left| {\mathop {{\text{PQ}}}\limits^ \to } \right| \times \left| {\mathop {{\text{PR}}}\limits^ \to } \right| \times \,\,{\text{sin}}\,P,\,\,\frac{1}{2} \times 6 \times \sqrt {46} \times \,\,{\text{sin}}\,0.582\)
area is 11.2 (sq. units) A1 N2
[2 marks]
recognizing shortest distance is perpendicular distance from R to line through P and Q (M1)
eg sketch, height of triangle with base \(\left[ {{\text{PQ}}} \right],\,\,\frac{1}{2} \times 6 \times h,\,\,{\text{sin}}\,33.3^\circ = \frac{h}{{\sqrt {46} }}\)
correct working (A1)
eg \(\frac{1}{2} \times 6 \times d = 11.2,\,\,\left| {\mathop {{\text{PR}}}\limits^ \to } \right| \times \,\,{\text{sin}}\,P,\,\,\sqrt {46} \times \,\,{\text{sin}}\,33.3^\circ \)
3.72677
distance = 3.73 (units) A1 N2
[3 marks]