Question
a.Consider the vectors a = 6i + 3j + 2k, b = −3j + 4k.
(i) Find the cosine of the angle between vectors a and b.
(ii) Find a \( \times \) b.
(iii) Hence find the Cartesian equation of the plane \(\prod \) containing the vectors a and b and passing through the point (1, 1, −1).
(iv) The plane \(\prod \) intersects the x-y plane in the line l. Find the area of the finite triangular region enclosed by l, the x-axis and the y-axis.[11]
Given two vectors p and q,
(i) show that p\( \cdot \)p = \(|\)p\({|^2}\);
(ii) hence, or otherwise, show that \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\);
(iii) deduce that \(|\)p + q\(|\) ≤ \(|\)p\(|\) + \(|\)q\(|\).[8]
▶️Answer/Explanation
Markscheme
(i) use of a\( \cdot \)b = \(|\)a\(|\)\(|\)b\(|\cos \theta \) (M1)
a\( \cdot \)b = –1 (A1)
\(|\)a\(|\) = 7, \(|\)b\(|\) = 5 (A1)
\(\cos \theta = – \frac{1}{{35}}\) A1
(ii) the required cross product is
\(\left| {\begin{array}{*{20}{c}}
i&j&k \\
6&3&2 \\
0&{ – 3}&4
\end{array}} \right| = \) 18i – 24j -18k M1A1
(iii) using r\( \cdot \)n = p\( \cdot \)n the equation of the plane is (M1)
\(18x – 24y – 18z = 12\,\,\,\,\,(3x – 4y – 3z = 2)\) A1
(iv) recognizing that z = 0 (M1)
x-intercept \( = \frac{2}{3}\), y-intercept \( = – \frac{1}{2}\) (A1)
area \( = \left( {\frac{2}{3}} \right)\left( {\frac{1}{2}} \right)\left( {\frac{1}{2}} \right) = \frac{1}{6}\) A1
[11 marks]
(i) p\( \cdot \)p = \(|\)p\(|\)\(|\)p\(|\cos 0\) M1A1
= \(|\)p\({|^2}\) AG
(ii) consider the LHS, and use of result from part (i)
\(|\)p + q\({|^2}\) = (p + q)\( \cdot \)(p + q) M1
= p\( \cdot \)p + p\( \cdot \)q + q\( \cdot \)p + q\( \cdot \)q (A1)
= p\( \cdot \)p + 2p\( \cdot \)q + q\( \cdot \)q A1
= \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) AG
(iii) EITHER
use of p\( \cdot \)q \( \leqslant \) \(|\)p\(|\)\(|\)q\(|\) M1
so 0 \( \leqslant \) \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) \( \leqslant \) \(|\)p\({|^2}\) + 2 \(|\)p\(|\)\(|\)q\(|\) + \(|\)q\({|^2}\) A1
take square root (of these positive quantities) to establish A1
\(|\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
OR
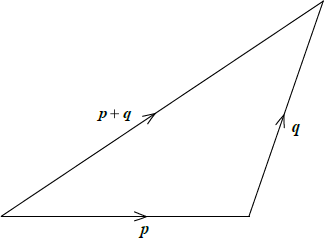 M1M1
M1M1
Note: Award M1 for correct diagram and M1 for correct labelling of vectors including arrows.
since the sum of any two sides of a triangle is greater than the third side,
\(|\)p\(|\) + \(|\)q\(|\) > \(|\)p + q\(|\) A1
when p and q are collinear \(|\)p\(|\) + \(|\)q\(|\) = \(|\)p + q\(|\)
\( \Rightarrow |\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
[8 marks]
Question
The vertices of a triangle ABC have coordinates given by A(−1, 2, 3), B(4, 1, 1) and C(3, −2, 2).
a.(i) Find the lengths of the sides of the triangle.
(ii) Find \(\cos {\rm{B\hat AC}}\).[6]
b.(i) Show that \(\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} = \) −7i − 3j − 16k.
(ii) Hence, show that the area of the triangle ABC is \(\frac{1}{2}\sqrt {314} \).[5]
c.Find the Cartesian equation of the plane containing the triangle ABC.[3]
d.Find a vector equation of (AB).[2]
e.The point D on (AB) is such that \(\overrightarrow {{\text{OD}}} \) is perpendicular to \(\overrightarrow {{\text{BC}}} \) where O is the origin.
(i) Find the coordinates of D.
(ii) Show that D does not lie between A and B.[5]
▶️Answer/Explanation
Markscheme
(i) \(\overrightarrow {{\text{AB}}} = \overrightarrow {{\text{OB}}} – \overrightarrow {{\text{OA}}} = \) 5i – j – 2k (or in column vector form) (A1)
Note: Award A1 if any one of the vectors, or its negative, representing the sides of the triangle is seen.
\(\overrightarrow {{\text{AB}}} = \) |5i – j – 2k|= \(\sqrt {30} \)
\(\overrightarrow {{\text{BC}}} = \) |–i – 3j + k|= \(\sqrt {11} \)
\(\overrightarrow {{\text{CA}}} = \) |–4i + 4j + k|= \(\sqrt {33} \) A2
Note: Award A1 for two correct and A0 for one correct.
(ii) METHOD 1
\(\cos {\text{BAC}} = \frac{{20 + 4 + 2}}{{\sqrt {30} \sqrt {33} }}\) M1A1
Note: Award M1 for an attempt at the use of the scalar product for two vectors representing the sides AB and AC, or their negatives, A1 for the correct computation using their vectors.
\( = \frac{{26}}{{\sqrt {990} }}{\text{ }}\left( { = \frac{{26}}{{3\sqrt {110} }}} \right)\) A1
Note: Candidates who use the modulus need to justify it – the angle is not stated in the question to be acute.
METHOD 2
using the cosine rule
\(\cos {\text{BAC}} = \frac{{30 + 33 – 11}}{{2\sqrt {30} \sqrt {33} }}\) M1A1
\( = \frac{{26}}{{\sqrt {990} }}{\text{ }}\left( { = \frac{{26}}{{3\sqrt {110} }}} \right)\) A1
[6 marks]
\(\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} = \left| {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&{ – 3}&1 \\
{ – 4}&4&1
\end{array}} \right|\) A1
\( = \left( {( – 3) \times 1 – 1 \times 4} \right)\)i + \(\left( {1 \times ( – 4) – ( – 1) \times 1} \right)\)j + \(\left( {( – 1) \times 4 – ( – 3) \times ( – 4)} \right)\)k M1A1
= –7i – 3j – 16k AG
(ii) the area of \(\Delta {\text{ABC}} = \frac{1}{2}\left| {\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} } \right|\) (M1)
\(\frac{1}{2}\sqrt {{{( – 7)}^2} + {{( – 3)}^2} + {{( – 16)}^2}} \) A1
\( = \frac{1}{2}\sqrt {314} \) AG
[5 marks]
attempt at the use of “(r – a)\( \cdot \)n = 0” (M1)
using r = xi + yj + zk, a = \(\overrightarrow {{\text{OA}}} \) and n = –7i – 3j – 16k (A1)
\(7x + 3y + 16z = 47\) A1
Note: Candidates who adopt a 2-parameter approach should be awarded, A1 for correct 2-parameter equations for x, y and z; M1 for a serious attempt at elimination of the parameters; A1 for the final Cartesian equation.
[3 marks]
r = \(\overrightarrow {{\text{OA}}} + t\overrightarrow {{\text{AB}}} \) (or equivalent) M1
r = (–i + 2j + 3k) + t (5i – j – 2k) A1
Note: Award M1A0 if “r =” is missing.
Note: Accept forms of the equation starting with B or with the direction reversed.
[2 marks]
(i) \(\overrightarrow {{\text{OD}}} = \) (–i + 2j + 3k) + t(5i – j – 2k)
statement that \(\overrightarrow {{\text{OD}}} \cdot \overrightarrow {{\text{BC}}} = 0\) (M1)
\(\left( {\begin{array}{*{20}{c}}
{ – 1 + 5t} \\
{2 – t} \\
{3 – 2t}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 3} \\
1
\end{array}} \right) = 0\) A1
\( – 2 – 4t = 0{\text{ or }}t = – \frac{1}{2}\) A1
coordinates of D are \(\left( { – \frac{7}{2},\frac{5}{2},4} \right)\) A1
Note: Different forms of \(\overrightarrow {{\text{OD}}} \) give different values of t, but the same final answer.
(ii) \(t < 0 \Rightarrow \) D is not between A and B R1
[5 marks]
Question
a.Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square.[3]
b.Find the coordinates of M, the mid-point of [OB].[1]
c.Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
d.Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]
e.Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
f.Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
g.(i) Find the angle \({\rm{O\hat DA}}\).
(ii) State what this tells you about the solid OABCDE.[6]
▶️Answer/Explanation
Markscheme
\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
Question
Two planes have equations
\[{\Pi _1}:{\text{ }}4x + y + z = 8{\text{ and }}{\Pi _2}:{\text{ }}4x + 3y – z = 0\]
Let \(L\) be the line of intersection of the two planes.
B is the point on \({\Pi _1}\) with coordinates \((a,{\text{ }}b,{\text{ }}1)\).
The point P lies on \(L\) and \({\rm{A\hat BP}} = 45^\circ \).
a.Find the cosine of the angle between the two planes in the form \(\sqrt {\frac{p}{q}} \) where \(p,{\text{ }}q \in \mathbb{Z}\).[4]
b.(i) Show that \(L\) has direction \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
(ii) Show that the point \({\text{A }}(1,{\text{ }}0,{\text{ }}4)\) lies on both planes.
(iii) Write down a vector equation of \(L\).[6]
c.Given the vector \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(L\) find the value of \(a\) and the value of \(b\).[5]
d.Show that \({\text{AB}} = 3\sqrt 2 \).[1]
e.Find the coordinates of the two possible positions of \(P\). [5]
▶️Answer/Explanation
Markscheme
Note: Throughout the question condone vectors written horizontally.
angle between planes is equal to the angles between the normal to the planes (M1)
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = 18\) (A1)
let \(\theta \) be the angle between the normal to the planes
\(\cos \theta = \frac{{18}}{{\sqrt {18} \sqrt {26} }} = \sqrt {\frac{{18}}{{26}}} {\text{ }}\left( {{\text{or equivalent, for example }}\sqrt {\frac{{324}}{{468}}} {\text{ or }}\sqrt {\frac{9}{{13}}} } \right)\) M1A1
[4 marks]
Note: Throughout the question condone vectors written horizontally.
(i) METHOD 1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right)\) M1A1
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
Note: Allow any equivalent wording or \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = 4\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\), do not allow \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
METHOD 2
let \(z = t\) (or equivalent)
solve simultaneously to get M1
\(y = t – 4,{\text{ }}x = 3 – 0.5t\) A1
hence direction vector is \(\left( {\begin{array}{*{20}{c}} { – 0.5} \\ 1 \\ 1 \end{array}} \right)\)
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
METHOD 3
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 2 + 2 = 0\) M1A1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 6 – 2 = 0\) A1
Note: If only one scalar product is found award M0A0A0.
(ii) \({\Pi _1}:{\text{ }}4 + 0 + 4 = 8\) and \({\Pi _2}:{\text{ }}4 + 0 – 4 = 0\) R1
(iii) r \( = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) A1A1
Note: A1 for “r \( = \)” and a correct point on the line, A1 for a parameter and a correct direction vector.
[6 marks]
Note: Throughout the question condone vectors written horizontally.
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right)\) (A1)
\(\left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\) M1
Note: Award M0 for \(\left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\).
\( – a + 1 + 2b – 6 = 0 \Rightarrow a – 2b = – 5\) A1
lies on \({\Pi _1}\) so \(4a + b + 1 = 8 \Rightarrow 4a + b = 7\) M1
\(a = 1,{\text{ }}b = 3\) A1
[5 marks]
Note: Throughout the question condone vectors written horizontally.
\({\text{AB}} = \sqrt {{0^2} + {3^2} + {{( – 3)}^2}} = 3\sqrt 2 \) M1AG
[1 mark]
Note: Throughout the question condone vectors written horizontally.
METHOD 1
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \left| {\overrightarrow {{\text{AP}}} } \right| = 3\sqrt 2 \) (M1)
\(\overrightarrow {{\text{AP}}} = t\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) (A1)
\(\left| {3t} \right| = 3\sqrt 2 \Rightarrow t = \pm \sqrt 2 \) (M1)A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
[5 marks]
METHOD 2
let P have coordinates \((1 – \lambda ,{\text{ }}2\lambda ,{\text{ }}4 + 2\lambda )\) M1
\(\overrightarrow {{\text{BA}}} = \left( {\begin{array}{*{20}{c}} 0 \\ { – 3} \\ 3 \end{array}} \right),{\text{ }}\overrightarrow {{\text{BP}}} = \left( {\begin{array}{*{20}{c}} { – \lambda } \\ {2\lambda – 3} \\ {3 + 2\lambda } \end{array}} \right)\) A1
\(\cos 45^\circ = \frac{{\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} }}{{\left| {{\text{BA}}} \right|\left| {{\text{BP}}} \right|}}\) M1
Note: Award M1 even if AB rather than BA is used in the scalar product.
\(\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} = 18\)
\(\frac{1}{{\sqrt 2 }} = \frac{{18}}{{\sqrt {18} \sqrt {9{\lambda ^2} + 18} }}\)
\(\lambda = \pm \sqrt 2 \) A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
Note: Accept answers given as position vectors.
[5 marks]
Examiners report
This was successfully done, though some candidates lost marks unnecessarily by not giving the answer in the form requested in the question.
(b)(i) A variety of techniques were successfully used here. A common error was not to justify why the vector obtained from the vector product was in the same direction as the one given in the question.
(b)(ii) and (iii) These were well done, though too many candidates still lose a mark unnecessarily by writing the vector equation of a line as \(l = \) rather than \(r = \).
Weaker candidates found the rest of this question more difficult. Though most obtained one equation for \(a\) and \(b\) they did not take note of the fact that it was also on the given plane, which gave the second equation.
This was done successfully by the majority of candidates. Candidates need to be aware that the notation AB means the length of the line segment joining the points A and B (as in the course guide).
This proved to be a difficult question for most candidates. Those who were successful were equally split between the two approaches given in the markscheme.
Question
The acute angle between the vectors 3i − 4j − 5k and 5i − 4j + 3k is denoted by θ.
Find cos θ.
▶️Answer/Explanation
Markscheme
cos θ = \(\frac{{\left( {3i – 4j – 5k} \right) \bullet \left( {5i – 4j + 3k} \right)}}{{\left| {3i – 4j – 5k} \right|\left| {5i – 4j + 3k} \right|}}\) (M1)
\( = \frac{{16}}{{\sqrt {50} \sqrt {50} }}\) A1A1
Note: A1 for correct numerator and A1 for correct denominator.
\( = \frac{8}{{25}}\left( { = \frac{{16}}{{50}} = 0.32} \right)\) A1
[4 marks]