Question
Consider the vectors a = 6i + 3j + 2k, b = −3j + 4k.
a.(i) Find the cosine of the angle between vectors a and b.
(ii) Find a \( \times \) b.
(iii) Hence find the Cartesian equation of the plane \(\prod \) containing the vectors a and b and passing through the point (1, 1, −1).
(iv) The plane \(\prod \) intersects the x-y plane in the line l. Find the area of the finite triangular region enclosed by l, the x-axis and the y-axis. [11]
(i) show that p\( \cdot \)p = \(|\)p\({|^2}\);
(ii) hence, or otherwise, show that \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\);
(iii) deduce that \(|\)p + q\(|\) ≤ \(|\)p\(|\) + \(|\)q\(|\). [8]
▶️Answer/Explanation
Markscheme
a.(i) use of a\( \cdot \)b = \(|\)a\(|\)\(|\)b\(|\cos \theta \) (M1)
a\( \cdot \)b = –1 (A1)
\(|\)a\(|\) = 7, \(|\)b\(|\) = 5 (A1)
\(\cos \theta = – \frac{1}{{35}}\) A1
(ii) the required cross product is
\(\left| {\begin{array}{*{20}{c}}
i&j&k \\
6&3&2 \\
0&{ – 3}&4
\end{array}} \right| = \) 18i – 24j -18k M1A1
(iii) using r\( \cdot \)n = p\( \cdot \)n the equation of the plane is (M1)
\(18x – 24y – 18z = 12\,\,\,\,\,(3x – 4y – 3z = 2)\) A1
(iv) recognizing that z = 0 (M1)
x-intercept \( = \frac{2}{3}\), y-intercept \( = – \frac{1}{2}\) (A1)
area \( = \left( {\frac{2}{3}} \right)\left( {\frac{1}{2}} \right)\left( {\frac{1}{2}} \right) = \frac{1}{6}\) A1
[11 marks]
(i) p\( \cdot \)p = \(|\)p\(|\)\(|\)p\(|\cos 0\) M1A1
= \(|\)p\({|^2}\) AG
(ii) consider the LHS, and use of result from part (i)
\(|\)p + q\({|^2}\) = (p + q)\( \cdot \)(p + q) M1
= p\( \cdot \)p + p\( \cdot \)q + q\( \cdot \)p + q\( \cdot \)q (A1)
= p\( \cdot \)p + 2p\( \cdot \)q + q\( \cdot \)q A1
= \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) AG
(iii) EITHER
use of p\( \cdot \)q \( \leqslant \) \(|\)p\(|\)\(|\)q\(|\) M1
so 0 \( \leqslant \) \(|\)p + q\({|^2}\) = \(|\)p\({|^2}\) + 2p\( \cdot \)q + \(|\)q\({|^2}\) \( \leqslant \) \(|\)p\({|^2}\) + 2 \(|\)p\(|\)\(|\)q\(|\) + \(|\)q\({|^2}\) A1
take square root (of these positive quantities) to establish A1
\(|\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
OR
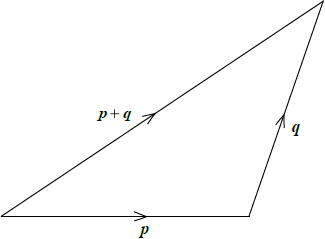 M1M1
M1M1
Note: Award M1 for correct diagram and M1 for correct labelling of vectors including arrows.
since the sum of any two sides of a triangle is greater than the third side,
\(|\)p\(|\) + \(|\)q\(|\) > \(|\)p + q\(|\) A1
when p and q are collinear \(|\)p\(|\) + \(|\)q\(|\) = \(|\)p + q\(|\)
\( \Rightarrow |\)p + q\(|\) \( \leqslant \) \(|\)p\(|\) + \(|\)q\(|\) AG
[8 marks]
Question
The diagram below shows a circle with centre O. The points A, B, C lie on the circumference of the circle and [AC] is a diameter.
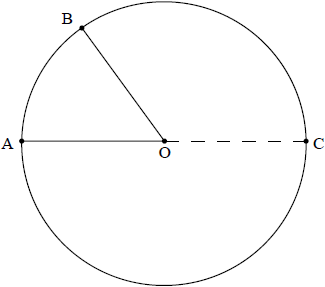
Let \(\overrightarrow {{\text{OA}}} = {\boldsymbol{a}}\) and \(\overrightarrow {{\text{OB}}} = {\boldsymbol{b}}\) .
a.Write down expressions for \(\overrightarrow {{\text{AB}}} \) and \(\overrightarrow {{\text{CB}}} \) in terms of the vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) . [2]
b. Hence prove that angle \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle.[3]
▶️Answer/Explanation
Markscheme
a.\(\overrightarrow {{\text{AB}}} = {\boldsymbol{b}} – {\boldsymbol{a}}\) A1
\(\overrightarrow {{\text{CB}}} = {\boldsymbol{a}} + {\boldsymbol{b}}\) A1
[2 marks]
\(\overrightarrow {{\text{AB}}} \cdot \overrightarrow {{\text{CB}}} = \left( {{\boldsymbol{b}} – {\boldsymbol{a}}} \right) \cdot \left( {{\boldsymbol{b}} + {\boldsymbol{a}}} \right)\) M1
\( = {\left| {\mathbf{b}} \right|^2} – {\left| {\mathbf{a}} \right|^2}\) A1
\( = 0\) since \(\left| {\boldsymbol{b}} \right| = \left| {\boldsymbol{a}} \right|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle AG [3 marks]
Question
In the diagram below, [AB] is a diameter of the circle with centre O. Point C is on the circumference of the circle. Let \(\overrightarrow {{\text{OB}}} = \boldsymbol{b} \) and \(\overrightarrow {{\text{OC}}} = \boldsymbol{c}\) .
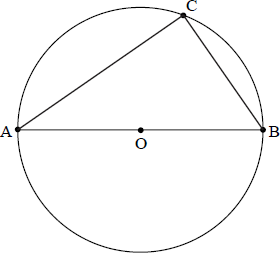
Find an expression for \(\overrightarrow {{\text{CB}}} \) and for \(\overrightarrow {{\text{AC}}} \) in terms of \(\boldsymbol{b}\) and \(\boldsymbol{c}\) .
Hence prove that \({\rm{A\hat CB}}\) is a right angle.
▶️Answer/Explanation
Markscheme
a.\(\overrightarrow {{\text{CB}}} = \boldsymbol{b} – \boldsymbol{c}\) , \(\overrightarrow {{\text{AC}}} = \boldsymbol{b} + \boldsymbol{c}\) A1A1
Note: Condone absence of vector notation in (a).
[2 marks]
\(\overrightarrow {{\text{AC}}} \cdot \overrightarrow {{\text{CB}}} = \)(b + c)\( \cdot \)(b – c) M1
= \(|\)b\({|^2}\) – \(|\)c\({|^2}\) A1
= 0 since \(|\)b\(|\) = \(|\)c\(|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AC}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\rm{A\hat CB}}\) is a right angle AG [3 marks]
Question
For non-zero vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\), show that
a.(i) if \(\left| {{\boldsymbol{a}} – {\boldsymbol{b}}} \right| = \left| {{\boldsymbol{a}} + {\boldsymbol{b}}} \right|\), then \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) are perpendicular;
(ii) \({\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {({\boldsymbol{a}} \cdot {\boldsymbol{b}})^2}\).[8]
The points A, B and C have position vectors \({\boldsymbol{a}}\), \({\boldsymbol{b}}\) and \({\boldsymbol{c}}\).
(i) Show that the area of triangle ABC is \(\frac{1}{2}\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|\).
(ii) Hence, show that the shortest distance from B to AC is
\[\frac{{\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|}}{{\left| {{\boldsymbol{c}} – {\boldsymbol{a}}} \right|}}{\text{.}}\] [7]
▶️Answer/Explanation
Markscheme
a.(i) \(\left| {{\boldsymbol{a}} – {\boldsymbol{b}}} \right| = \left| {{\boldsymbol{a}} + {\boldsymbol{b}}} \right|\)
\( \Rightarrow \left( {{\boldsymbol{a}} – {\boldsymbol{b}}} \right) \cdot \left( {{\boldsymbol{a}} – {\boldsymbol{b}}} \right) = \left( {{\boldsymbol{a}} + {\boldsymbol{b}}} \right) \cdot \left( {{\boldsymbol{a}} + {\boldsymbol{b}}} \right)\) (M1)
\( \Rightarrow {\left| {\boldsymbol{a}} \right|^2} – 2{\boldsymbol{a}} \cdot {\boldsymbol{b}} + {\left| {\boldsymbol{b}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2} + 2{\boldsymbol{a}} \cdot {\boldsymbol{b}} + {\left| {\boldsymbol{b}} \right|^2}\) A1
\( \Rightarrow 4{\boldsymbol{a}} \cdot {\boldsymbol{b}} = 0 \Rightarrow {\boldsymbol{a}} \cdot {\boldsymbol{b}} = 0\) A1
therefore \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) are perpendicular R1
Note: Allow use of 2-d components.
Note: Do not condone sloppy vector notation, so we must see something to the effect that \({\left| {\boldsymbol{c}} \right|^2} = {\boldsymbol{c}} \cdot {\boldsymbol{c}}\) is clearly being used for the M1.
Note: Allow a correct geometric argument, for example that the diagonals of a parallelogram have the same length only if it is a rectangle.
(ii) \({\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left( {\left| {\boldsymbol{a}} \right|\left| {\boldsymbol{b}} \right|\sin \theta } \right)^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}{\sin ^2}\theta \) M1A1
\({\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left( {{\boldsymbol{a}} \cdot {\boldsymbol{b}}} \right)^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}{\cos ^2}\theta \) M1
\( = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}\left( {1 – {{\cos }^2}\theta } \right)\) A1
\( = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}\left( {{{\sin }^2}\theta } \right)\)
\( \Rightarrow {\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left( {{\boldsymbol{a}} \cdot {\boldsymbol{b}}} \right)^2}\) AG [8 marks]
(i) area of triangle \( = \frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|\) (M1)
\( = \frac{1}{2}\left| {\left( {{\boldsymbol{b}} – {\boldsymbol{a}}} \right) \times \left( {{\boldsymbol{c}} – {\boldsymbol{a}}} \right)} \right|\) A1
\( = \frac{1}{2}\left| {{\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{b}} \times {\boldsymbol{ – a}} + {\boldsymbol{ – a}} \times {\boldsymbol{c}} + {\boldsymbol{ – a}} \times {\boldsymbol{ – a}}} \right|\) A1
\({\boldsymbol{b}} \times {\boldsymbol{ – a}} = {\boldsymbol{a}} \times {\boldsymbol{b}}\); \({\boldsymbol{c}} \times {\boldsymbol{a}} = {\boldsymbol{ – a}} \times {\boldsymbol{c}}\); \({\boldsymbol{ – a}} \times {\boldsymbol{ – a}} = 0\) M1
hence, area of triangle is \(\frac{1}{2}\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|\) AG
(ii) D is the foot of the perpendicular from B to AC
area of triangle \({\text{ABC}} = \frac{1}{2}\left| {\overrightarrow {{\text{AC}}} } \right|\left| {\overrightarrow {{\text{BD}}} } \right|\) A1
therefore
\(\frac{1}{2}\left| {\overrightarrow {{\text{AC}}} } \right|\left| {\overrightarrow {{\text{BD}}} } \right| = \frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|\) M1
hence, \(\left| {\overrightarrow {{\text{BD}}} } \right| = \frac{{\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|}}{{\left| {\overrightarrow {{\text{AC}}} } \right|}}\) A1
\( = \frac{{\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|}}{{\left| {{\boldsymbol{c}} – {\boldsymbol{a}}} \right|}}\) AG
[7 marks]
Question
a.For non-zero vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\), show that
(i) if \(\left| {{\boldsymbol{a}} – {\boldsymbol{b}}} \right| = \left| {{\boldsymbol{a}} + {\boldsymbol{b}}} \right|\), then \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) are perpendicular;
(ii) \({\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {({\boldsymbol{a}} \cdot {\boldsymbol{b}})^2}\). [8]
The points A, B and C have position vectors \({\boldsymbol{a}}\), \({\boldsymbol{b}}\) and \({\boldsymbol{c}}\).
(i) Show that the area of triangle ABC is \(\frac{1}{2}\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|\).
(ii) Hence, show that the shortest distance from B to AC is
\[\frac{{\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|}}{{\left| {{\boldsymbol{c}} – {\boldsymbol{a}}} \right|}}{\text{.}}\] [7]
▶️Answer/Explanation
Markscheme
a.(i) \(\left| {{\boldsymbol{a}} – {\boldsymbol{b}}} \right| = \left| {{\boldsymbol{a}} + {\boldsymbol{b}}} \right|\)
\( \Rightarrow \left( {{\boldsymbol{a}} – {\boldsymbol{b}}} \right) \cdot \left( {{\boldsymbol{a}} – {\boldsymbol{b}}} \right) = \left( {{\boldsymbol{a}} + {\boldsymbol{b}}} \right) \cdot \left( {{\boldsymbol{a}} + {\boldsymbol{b}}} \right)\) (M1)
\( \Rightarrow {\left| {\boldsymbol{a}} \right|^2} – 2{\boldsymbol{a}} \cdot {\boldsymbol{b}} + {\left| {\boldsymbol{b}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2} + 2{\boldsymbol{a}} \cdot {\boldsymbol{b}} + {\left| {\boldsymbol{b}} \right|^2}\) A1
\( \Rightarrow 4{\boldsymbol{a}} \cdot {\boldsymbol{b}} = 0 \Rightarrow {\boldsymbol{a}} \cdot {\boldsymbol{b}} = 0\) A1
therefore \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) are perpendicular R1
Note: Allow use of 2-d components.
Note: Do not condone sloppy vector notation, so we must see something to the effect that \({\left| {\boldsymbol{c}} \right|^2} = {\boldsymbol{c}} \cdot {\boldsymbol{c}}\) is clearly being used for the M1.
Note: Allow a correct geometric argument, for example that the diagonals of a parallelogram have the same length only if it is a rectangle.
(ii) \({\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left( {\left| {\boldsymbol{a}} \right|\left| {\boldsymbol{b}} \right|\sin \theta } \right)^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}{\sin ^2}\theta \) M1A1
\({\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left( {{\boldsymbol{a}} \cdot {\boldsymbol{b}}} \right)^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}{\cos ^2}\theta \) M1
\( = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}\left( {1 – {{\cos }^2}\theta } \right)\) A1
\( = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2}\left( {{{\sin }^2}\theta } \right)\)
\( \Rightarrow {\left| {{\boldsymbol{a}} \times {\boldsymbol{b}}} \right|^2} = {\left| {\boldsymbol{a}} \right|^2}{\left| {\boldsymbol{b}} \right|^2} – {\left( {{\boldsymbol{a}} \cdot {\boldsymbol{b}}} \right)^2}\) AG
[8 marks]
(i) area of triangle \( = \frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|\) (M1)
\( = \frac{1}{2}\left| {\left( {{\boldsymbol{b}} – {\boldsymbol{a}}} \right) \times \left( {{\boldsymbol{c}} – {\boldsymbol{a}}} \right)} \right|\) A1
\( = \frac{1}{2}\left| {{\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{b}} \times {\boldsymbol{ – a}} + {\boldsymbol{ – a}} \times {\boldsymbol{c}} + {\boldsymbol{ – a}} \times {\boldsymbol{ – a}}} \right|\) A1
\({\boldsymbol{b}} \times {\boldsymbol{ – a}} = {\boldsymbol{a}} \times {\boldsymbol{b}}\); \({\boldsymbol{c}} \times {\boldsymbol{a}} = {\boldsymbol{ – a}} \times {\boldsymbol{c}}\); \({\boldsymbol{ – a}} \times {\boldsymbol{ – a}} = 0\) M1
hence, area of triangle is \(\frac{1}{2}\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|\) AG
(ii) D is the foot of the perpendicular from B to AC
area of triangle \({\text{ABC}} = \frac{1}{2}\left| {\overrightarrow {{\text{AC}}} } \right|\left| {\overrightarrow {{\text{BD}}} } \right|\) A1
therefore
\(\frac{1}{2}\left| {\overrightarrow {{\text{AC}}} } \right|\left| {\overrightarrow {{\text{BD}}} } \right| = \frac{1}{2}\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|\) M1
hence, \(\left| {\overrightarrow {{\text{BD}}} } \right| = \frac{{\left| {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} } \right|}}{{\left| {\overrightarrow {{\text{AC}}} } \right|}}\) A1
\( = \frac{{\left| {{\boldsymbol{a}} \times {\boldsymbol{b}} + {\boldsymbol{b}} \times {\boldsymbol{c}} + {\boldsymbol{c}} \times {\boldsymbol{a}}} \right|}}{{\left| {{\boldsymbol{c}} – {\boldsymbol{a}}} \right|}}\) AG
[7 marks]
Question
The vertices of a triangle ABC have coordinates given by A(−1, 2, 3), B(4, 1, 1) and C(3, −2, 2).
a.(i) Find the lengths of the sides of the triangle.
(ii) Find \(\cos {\rm{B\hat AC}}\).[6]
(i) Show that \(\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} = \) −7i − 3j − 16k.
(ii) Hence, show that the area of the triangle ABC is \(\frac{1}{2}\sqrt {314} \).[5]
(i) Find the coordinates of D.
(ii) Show that D does not lie between A and B. [5]
▶️Answer/Explanation
Markscheme
a.(i) \(\overrightarrow {{\text{AB}}} = \overrightarrow {{\text{OB}}} – \overrightarrow {{\text{OA}}} = \) 5i – j – 2k (or in column vector form) (A1)
Note: Award A1 if any one of the vectors, or its negative, representing the sides of the triangle is seen.
\(\overrightarrow {{\text{AB}}} = \) |5i – j – 2k|= \(\sqrt {30} \)
\(\overrightarrow {{\text{BC}}} = \) |–i – 3j + k|= \(\sqrt {11} \)
\(\overrightarrow {{\text{CA}}} = \) |–4i + 4j + k|= \(\sqrt {33} \) A2
Note: Award A1 for two correct and A0 for one correct.
(ii) METHOD 1
\(\cos {\text{BAC}} = \frac{{20 + 4 + 2}}{{\sqrt {30} \sqrt {33} }}\) M1A1
Note: Award M1 for an attempt at the use of the scalar product for two vectors representing the sides AB and AC, or their negatives, A1 for the correct computation using their vectors.
\( = \frac{{26}}{{\sqrt {990} }}{\text{ }}\left( { = \frac{{26}}{{3\sqrt {110} }}} \right)\) A1
Note: Candidates who use the modulus need to justify it – the angle is not stated in the question to be acute.
METHOD 2
using the cosine rule
\(\cos {\text{BAC}} = \frac{{30 + 33 – 11}}{{2\sqrt {30} \sqrt {33} }}\) M1A1
\( = \frac{{26}}{{\sqrt {990} }}{\text{ }}\left( { = \frac{{26}}{{3\sqrt {110} }}} \right)\) A1
[6 marks]
\(\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} = \left| {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&{ – 3}&1 \\
{ – 4}&4&1
\end{array}} \right|\) A1
\( = \left( {( – 3) \times 1 – 1 \times 4} \right)\)i + \(\left( {1 \times ( – 4) – ( – 1) \times 1} \right)\)j + \(\left( {( – 1) \times 4 – ( – 3) \times ( – 4)} \right)\)k M1A1
= –7i – 3j – 16k AG
(ii) the area of \(\Delta {\text{ABC}} = \frac{1}{2}\left| {\overrightarrow {{\text{BC}}} \times \overrightarrow {{\text{CA}}} } \right|\) (M1)
\(\frac{1}{2}\sqrt {{{( – 7)}^2} + {{( – 3)}^2} + {{( – 16)}^2}} \) A1
\( = \frac{1}{2}\sqrt {314} \) AG
[5 marks]
attempt at the use of “(r – a)\( \cdot \)n = 0” (M1)
using r = xi + yj + zk, a = \(\overrightarrow {{\text{OA}}} \) and n = –7i – 3j – 16k (A1)
\(7x + 3y + 16z = 47\) A1
Note: Candidates who adopt a 2-parameter approach should be awarded, A1 for correct 2-parameter equations for x, y and z; M1 for a serious attempt at elimination of the parameters; A1 for the final Cartesian equation.
[3 marks]
r = \(\overrightarrow {{\text{OA}}} + t\overrightarrow {{\text{AB}}} \) (or equivalent) M1
r = (–i + 2j + 3k) + t (5i – j – 2k) A1
Note: Award M1A0 if “r =” is missing.
Note: Accept forms of the equation starting with B or with the direction reversed.
[2 marks]
(i) \(\overrightarrow {{\text{OD}}} = \) (–i + 2j + 3k) + t(5i – j – 2k)
statement that \(\overrightarrow {{\text{OD}}} \cdot \overrightarrow {{\text{BC}}} = 0\) (M1)
\(\left( {\begin{array}{*{20}{c}}
{ – 1 + 5t} \\
{2 – t} \\
{3 – 2t}
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 3} \\
1
\end{array}} \right) = 0\) A1
\( – 2 – 4t = 0{\text{ or }}t = – \frac{1}{2}\) A1
coordinates of D are \(\left( { – \frac{7}{2},\frac{5}{2},4} \right)\) A1
Note: Different forms of \(\overrightarrow {{\text{OD}}} \) give different values of t, but the same final answer.
(ii) \(t < 0 \Rightarrow \) D is not between A and B R1 [5 marks]
Question
PQRS is a rhombus. Given that \(\overrightarrow {{\text{PQ}}} = \) \(\boldsymbol{a}\) and \(\overrightarrow {{\text{QR}}} = \) \(\boldsymbol{b}\),
(a) express the vectors \(\overrightarrow {{\text{PR}}} \) and \(\overrightarrow {{\text{QS}}} \) in terms of \(\boldsymbol{a}\) and \(\boldsymbol{b}\);
(b) hence show that the diagonals in a rhombus intersect at right angles.
▶️Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{PR}}} = \) a + b A1
\(\overrightarrow {{\text{QS}}} = \) b − a A1
[2 marks]
(b) \(\overrightarrow {{\text{PR}}} \cdot \overrightarrow {{\text{QS}}} = \) (a + b) \( \cdot \) (b − a) M1
\( = |\)b\({|^2} – |\)a\({|^2}\) A1
for a rhombus \(|\)a\(| = |\)b\(|\) R1
hence \(|\)b\({|^2} – |\)a\({|^2} = 0\) A1
Note: Do not award the final A1 unless R1 is awarded.
hence the diagonals intersect at right angles AG
[4 marks]
Total [6 marks]
Examiners report
Question
a. Two planes have equations
\[{\Pi _1}:{\text{ }}4x + y + z = 8{\text{ and }}{\Pi _2}:{\text{ }}4x + 3y – z = 0\]
Let \(L\) be the line of intersection of the two planes.
B is the point on \({\Pi _1}\) with coordinates \((a,{\text{ }}b,{\text{ }}1)\).
The point P lies on \(L\) and \({\rm{A\hat BP}} = 45^\circ \).
Find the cosine of the angle between the two planes in the form \(\sqrt {\frac{p}{q}} \) where \(p,{\text{ }}q \in \mathbb{Z}\).[4]
(i) Show that \(L\) has direction \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
(ii) Show that the point \({\text{A }}(1,{\text{ }}0,{\text{ }}4)\) lies on both planes.
(iii) Write down a vector equation of \(L\).[6]
c.Given the vector \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(L\) find the value of \(a\) and the value of \(b\).[5]
d.Show that \({\text{AB}} = 3\sqrt 2 \).[1]
e. Find the coordinates of the two possible positions of \(P\).[5]
▶️Answer/Explanation
Markscheme
a.Note: Throughout the question condone vectors written horizontally.
angle between planes is equal to the angles between the normal to the planes (M1)
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = 18\) (A1)
let \(\theta \) be the angle between the normal to the planes
\(\cos \theta = \frac{{18}}{{\sqrt {18} \sqrt {26} }} = \sqrt {\frac{{18}}{{26}}} {\text{ }}\left( {{\text{or equivalent, for example }}\sqrt {\frac{{324}}{{468}}} {\text{ or }}\sqrt {\frac{9}{{13}}} } \right)\) M1A1
[4 marks]
Note: Throughout the question condone vectors written horizontally.
(i) METHOD 1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right)\) M1A1
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
Note: Allow any equivalent wording or \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = 4\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\), do not allow \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
METHOD 2
let \(z = t\) (or equivalent)
solve simultaneously to get M1
\(y = t – 4,{\text{ }}x = 3 – 0.5t\) A1
hence direction vector is \(\left( {\begin{array}{*{20}{c}} { – 0.5} \\ 1 \\ 1 \end{array}} \right)\)
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
METHOD 3
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 2 + 2 = 0\) M1A1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 6 – 2 = 0\) A1
Note: If only one scalar product is found award M0A0A0.
(ii) \({\Pi _1}:{\text{ }}4 + 0 + 4 = 8\) and \({\Pi _2}:{\text{ }}4 + 0 – 4 = 0\) R1
(iii) r \( = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) A1A1
Note: A1 for “r \( = \)” and a correct point on the line, A1 for a parameter and a correct direction vector. [6 marks]
Note: Throughout the question condone vectors written horizontally.
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right)\) (A1)
\(\left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\) M1
Note: Award M0 for \(\left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\).
\( – a + 1 + 2b – 6 = 0 \Rightarrow a – 2b = – 5\) A1
lies on \({\Pi _1}\) so \(4a + b + 1 = 8 \Rightarrow 4a + b = 7\) M1
\(a = 1,{\text{ }}b = 3\) A1
[5 marks]
Note: Throughout the question condone vectors written horizontally.
\({\text{AB}} = \sqrt {{0^2} + {3^2} + {{( – 3)}^2}} = 3\sqrt 2 \) M1AG
[1 mark]
Note: Throughout the question condone vectors written horizontally.
METHOD 1
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \left| {\overrightarrow {{\text{AP}}} } \right| = 3\sqrt 2 \) (M1)
\(\overrightarrow {{\text{AP}}} = t\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) (A1)
\(\left| {3t} \right| = 3\sqrt 2 \Rightarrow t = \pm \sqrt 2 \) (M1)A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
[5 marks]
METHOD 2
let P have coordinates \((1 – \lambda ,{\text{ }}2\lambda ,{\text{ }}4 + 2\lambda )\) M1
\(\overrightarrow {{\text{BA}}} = \left( {\begin{array}{*{20}{c}} 0 \\ { – 3} \\ 3 \end{array}} \right),{\text{ }}\overrightarrow {{\text{BP}}} = \left( {\begin{array}{*{20}{c}} { – \lambda } \\ {2\lambda – 3} \\ {3 + 2\lambda } \end{array}} \right)\) A1
\(\cos 45^\circ = \frac{{\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} }}{{\left| {{\text{BA}}} \right|\left| {{\text{BP}}} \right|}}\) M1
Note: Award M1 even if AB rather than BA is used in the scalar product.
\(\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} = 18\)
\(\frac{1}{{\sqrt 2 }} = \frac{{18}}{{\sqrt {18} \sqrt {9{\lambda ^2} + 18} }}\)
\(\lambda = \pm \sqrt 2 \) A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
Note: Accept answers given as position vectors.
[5 marks]