Question
The position vector at time \(t\) of a point \(P\) is given by\[\overrightarrow {{\text{OP}}} = \left( {1 + t} \right){\boldsymbol{i}} + \left( {2 – 2t} \right){\boldsymbol{j}} + \left( {3t – 1} \right){\boldsymbol{k}},{\text{ }}t \geqslant 0.\]
(a) Find the coordinates of P when \(t = 0\) .
(b) Show that P moves along the line \(L\) with Cartesian equations\[x – 1 = \frac{{y – 2}}{{ – 2}} = \frac{{z + 1}}{3}\]
(c) (i) Find the value of t when P lies on the plane with equation \(2x + y + z = 6\) .
(ii) State the coordinates of P at this time.
(iii) Hence find the total distance travelled by P before it meets the plane.
The position vector at time \(t\) of another point, Q, is given by\[\overrightarrow {{\text{OQ}}} = \left( {\begin{array}{*{20}{c}}
{{t^2}} \\
{1 – t} \\
{1 – {t^2}}
\end{array}} \right),{\text{ }}t \geqslant 0.\]
(d) (i) Find the value of t for which the distance from Q to the origin is minimum.
(ii) Find the coordinates of Q at this time.
(e) Let \(\boldsymbol{a}\) , \(\boldsymbol{b}\) and \(\boldsymbol{c}\) be the position vectors of Q at times \(t = 0\), \(t =1\) and \(t = 2\) respectively.
(i) Show that the equation \({\boldsymbol{a}} – {\boldsymbol{b}} = k\left( {{\boldsymbol{b}} – {\boldsymbol{c}}} \right)\) has no solution for \(k\) .
(ii) Hence show that the path of Q is not a straight line.
Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{OP}}} = {\boldsymbol{i}} + 2{\boldsymbol{j}} – {\boldsymbol{k}}\) (M1)
the coordinates of P are (1, 2, –1) A1
[2 marks]
(b) EITHER
\(x = 1 + t\) , \(y = 2 – 2t\) , \(z = 3t – 1\) M1
\(x – 1 = t\) , \(\frac{{y – 2}}{{ – 2}} = t\) , \(\frac{{z + 1}}{3} = t\) A1
\(x – 1 = \frac{{y – 2}}{{ – 2}} = \frac{{z + 1}}{3}\) AG N0
OR
\(\left( {\begin{array}{*{20}{c}}
x \\
y \\
z
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
{ – 1}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
1 \\
{ – 2} \\
3
\end{array}} \right)\) M1A1
\(x – 1 = \frac{{y – 2}}{{ – 2}} = \frac{{z + 1}}{3}\) AG
[2 marks]
(c) (i) \(2\left( {1 + t} \right) + \left( {2 – 2t} \right) + \left( {3t – 1} \right) = 6 \Rightarrow t = 1\) M1A1 N1
(ii) coordinates are (2, 0, 2) A1
Note: Award A0 for position vector.
(iii) distance travelled is the distance between the two points (M1)
\(\sqrt {{{\left( {2 – 1} \right)}^2} + {{\left( {0 – 2} \right)}^2} + {{\left( {2 + 1} \right)}^2}} = \sqrt {14} \) (\( = 3.74\)) (M1)A1
[6 marks]
(d) (i) distance from Q to the origin is given by
\(d(t) = \sqrt {{t^4} + {{\left( {1 – t} \right)}^2} + {{\left( {1 – {t^2}} \right)}^2}} \) (or equivalent) M1A1
e.g. for labelled sketch of graph of \(d\) or \({d^2}\) (M1)(A1)
 or
or 
the minimum value is obtained for \(t = 0.761\) A1 N3
(ii) the coordinates are (0.579, 0.239, 0.421) A1
Note: Accept answers given as a position vector.
[6 marks]
(e) (i) \({\boldsymbol{a}} = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
1
\end{array}} \right)\), \({\boldsymbol{b}} = \left( {\begin{array}{*{20}{c}}
1 \\
0 \\
0
\end{array}} \right)\) and \({\boldsymbol{c}} = \left( {\begin{array}{*{20}{c}}
4 \\
{ – 1} \\
{ – 3}
\end{array}} \right)\) (M1)A1
substituting in the equation \({\boldsymbol{a}} – {\boldsymbol{b}} = k\left( {{\boldsymbol{b}} – {\boldsymbol{c}}} \right)\) , we have (M1)
\(\left( {\begin{array}{*{20}{c}}
0 \\
1 \\
1
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1 \\
0 \\
0
\end{array}} \right) = k\left( {\left( {\begin{array}{*{20}{c}}
1 \\
0 \\
0
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
4 \\
{ – 1} \\
{ – 3}
\end{array}} \right)} \right) \Leftrightarrow \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = k\left( {\begin{array}{*{20}{c}}
{ – 3} \\
1 \\
3
\end{array}} \right)\) A1
\( \Rightarrow k = 1\) and \(k = \frac{1}{3}\) which is impossible
so there is no solution for \(k\) R1
(ii) \({{\text{BA}}}\)and \(\overrightarrow {{\text{CB}}} \)are not parallel R2
(hence A, B, and C cannot be collinear)
Note: Only accept answers that follow from part (i).
[7 marks]
Total [23 marks]
Examiners report
Generally this question was answered well by those students who attempted it. It was common to see confusion between coordinates and position vectors. Part (d) was most easily answered with the use of a GDC, but fewer candidates took advantage of this. In part (e) many students had difficulties expressing their reasoning well to obtain the marks.
Question
Port A is defined to be the origin of a set of coordinate axes and port B is located at the point (70, 30), where distances are measured in kilometres. A ship S1 sails from port A at 10:00 in a straight line such that its position \(t\) hours after 10:00 is given by \(r = t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right)\).
A speedboat S2 is capable of three times the speed of S1 and is to meet S1 by travelling the shortest possible distance. What is the latest time that S2 can leave port B?
Answer/Explanation
Markscheme
METHOD 1
equation of journey of ship S1
\({r_1} = t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right)\)
equation of journey of speedboat S2 ,setting off \(k\) minutes later
\({r_2} = \left( {\begin{array}{*{20}{c}}
{70} \\
{30}
\end{array}} \right) + \left( {t – k} \right)\left( {\begin{array}{*{20}{c}}
{ – 60} \\
{30}
\end{array}} \right)\) M1A1A1
Note: Award M1 for perpendicular direction, A1 for speed, A1 for change in parameter (e.g. by using \(t – k\) or \(T\), \(k\) being the time difference between the departure of the ships).
solve \(t\left( {\begin{array}{*{20}{c}}
{10} \\
{20}
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{70} \\
{30}
\end{array}} \right) + \left( {t – k} \right)\left( {\begin{array}{*{20}{c}}
{ – 60} \\
{30}
\end{array}} \right)\) (M1)
Note: M mark is for equating their two expressions.
\(10t = 70 – 60t + 60k\)
\(20t = 30 + 30t – 30k\) M1
Note: M mark is for obtaining two equations involving two different parameters.
\(7t – 6k = 7\)
\( – t + 3k = 3\)
\(k = \frac{{28}}{{15}}\) A1
latest time is 11:52 A1
[7 marks]
METHOD 2
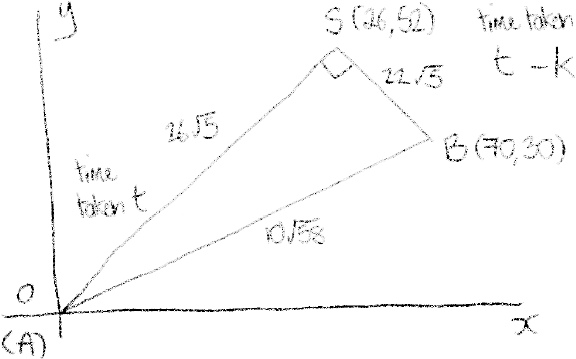
\({\text{SB}} = 22\sqrt 5 \) M1A1
(by perpendicular distance)
\({\text{SA}} = 26\sqrt 5 \) M1A1
(by Pythagoras or coordinates)
\(t = \frac{{26\sqrt 5 }}{{10\sqrt 5 }}\) A1
\(t – k = \frac{{22\sqrt 5 }}{{30\sqrt 5 }}\) A1
\(k = \frac{{28}}{{15}}\) leading to latest time 11:52 A1
[7 marks]
Examiners report
Few candidates managed to make progress on this question. Many candidates did not attempt the problem and many that did make an attempt failed to draw a diagram that would have allowed them to make further progress. There were a variety of possible solution techniques but candidates seemed unable to interpret the equation of a straight line written in vector form or find a perpendicular direction. This meant that it was very difficult for meaningful progress to be made towards a solution.
Question
Ed walks in a straight line from point \({\text{P}}( – 1,{\text{ }}4)\) to point \({\text{Q}}(4,{\text{ }}16)\) with constant speed.
Ed starts from point \(P\) at time \(t = 0\) and arrives at point \(Q\) at time \(t = 3\), where \(t\) is measured in hours.
Given that, at time \(t\), Ed’s position vector, relative to the origin, can be given in the form, \({{r}} = {{a}} + t{{b}}\),
find the vectors \({{a}}\) and \({{b}}\).
Roderick is at a point \({\text{C}}(11,{\text{ }}9)\). During Ed’s walk from \(P\) to \(Q\) Roderick wishes to signal to Ed. He decides to signal when Ed is at the closest point to \(C\).
Find the time when Roderick signals to Ed.
Answer/Explanation
Markscheme
\({{a}} = \left( {\begin{array}{*{20}{c}} { – 1} \\ 4 \end{array}} \right)\) A1
\({{b}} = \frac{1}{3}\left( {\left( {\begin{array}{*{20}{c}} 4 \\ {16} \end{array}} \right) – \left( {\begin{array}{*{20}{c}} { – 1} \\ 4 \end{array}} \right)} \right) = \left( {\begin{array}{*{20}{c}} {\frac{5}{3}} \\ 4 \end{array}} \right)\) (M1)A1
[3 marks]
METHOD 1
Roderick must signal in a direction vector perpendicular to Ed’s path. (M1)
the equation of the signal is \({\mathbf{s}} = \left( {\begin{array}{*{20}{c}} {11} \\ 9 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { – 12} \\ 5 \end{array}} \right)\;\;\;\)(or equivalent) A1
\(\left( {\begin{array}{*{20}{c}} { – 1} \\ 4 \end{array}} \right) + \frac{t}{3}\left( {\begin{array}{*{20}{c}} 5 \\ {12} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {11} \\ 9 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { – 12} \\ 5 \end{array}} \right)\) M1
\(\frac{5}{3}t + 12\lambda = 12\) and \(4t – 5\lambda = 5\) M1
\(t = 2.13\;\;\;\left( { = \frac{{360}}{{169}}} \right)\) A1
METHOD 2
\(\left( {\begin{array}{*{20}{c}} 5 \\ {12} \end{array}} \right) \bullet \left( {\left( {\begin{array}{*{20}{c}} {11} \\ 9 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} { – 1 + \frac{5}{3}t} \\ {4 + 4t} \end{array}} \right)} \right) = 0\;\;\;\)(or equivalent) M1A1A1
Note: Award the M1 for an attempt at a scalar product equated to zero, A1 for the first factor and A1 for the complete second factor.
attempting to solve for \(t\) (M1)
\(t = 2.13\;\;\;\left( {\frac{{360}}{{169}}} \right)\) A1
METHOD 3
\(x = \sqrt {{{\left( {12 – \frac{{5t}}{3}} \right)}^2} + {{(5 – 4t)}^2}} \;\;\;\)(or equivalent)\(\;\;\;\left( {{x^2} = {{\left( {12 – \frac{{5t}}{3}} \right)}^2} + {{(5 – 4t)}^2}} \right)\) M1A1A1
Note: Award M1 for use of Pythagoras’ theorem, A1 for \({\left( {12 – \frac{{5t}}{3}} \right)^2}\) and A1 for \({(5 – 4t)^2}\).
attempting (graphically or analytically) to find \(t\) such that \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 0\left( {\frac{{{\text{d}}({x^2})}}{{{\text{d}}t}} = 0} \right)\) (M1)
\(t = 2.13\;\;\;\left( { = \frac{{360}}{{169}}} \right)\) A1
METHOD 4
\(\cos \theta = \frac{{\left( {\begin{array}{*{20}{c}} {12} \\ 5 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 5 \\ {12} \end{array}} \right)}}{{\left| {\left( {\begin{array}{*{20}{c}} {12} \\ 5 \end{array}} \right)} \right|\left| {\left( {\begin{array}{*{20}{c}} 5 \\ {12} \end{array}} \right)} \right|}} = \frac{{120}}{{169}}\) M1A1
Note: Award M1 for attempting to calculate the scalar product.
\(\frac{{120}}{{13}} = \frac{t}{3}\left| {\left( {\begin{array}{*{20}{c}} 5 \\ {12} \end{array}} \right)} \right|\;\;\;\)(or equivalent) (A1)
attempting to solve for \(t\) (M1)
\(t = 2.13\;\;\;\left( { = \frac{{360}}{{169}}} \right)\) A1
[5 marks]
Total [8 marks]
Examiners report
[N/A]
[N/A]
