Question
The diagram shows a cube OABCDEFG.
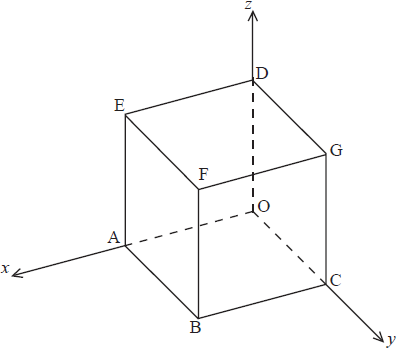
Let O be the origin, (OA) the x-axis, (OC) the y-axis and (OD) the z-axis.
Let M, N and P be the midpoints of [FG], [DG] and [CG], respectively.
The coordinates of F are (2, 2, 2).
(a) Find the position vectors \(\overrightarrow {{\text{OM}}} \), \(\overrightarrow {{\text{ON}}} \) and \(\overrightarrow {{\text{OP}}} \) in component form.
(b) Find \(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} \).
(c) Hence,
(i) calculate the area of the triangle MNP;
(ii) show that the line (AG) is perpendicular to the plane MNP;
(iii) find the equation of the plane MNP.
(d) Determine the coordinates of the point where the line (AG) meets the plane MNP.
▶️Answer/Explanation
Markscheme
(a) \(\overrightarrow {{\text{OM}}} = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right)\), \(\overrightarrow {{\text{ON}}} = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
2
\end{array}} \right)\) and \(\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
1
\end{array}} \right)\) A1A1A1
[3 marks]
(b) \(\overrightarrow {{\text{MP}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
0 \\
{ – 1}
\end{array}} \right)\) and \(\overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{ – 1} \\
0
\end{array}} \right)\) A1A1
\(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} = \left( {\begin{array}{*{20}{c}}
i&j&k \\
{ – 1}&0&{ – 1} \\
{ – 1}&{ – 1}&0
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) (M1)A1
[4 marks]
(c) (i) area of MNP \( = \frac{1}{2}\left| {\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} } \right|\) M1
\( = \frac{1}{2}\left| {\left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)} \right|\)
\( = \frac{{\sqrt 3 }}{2}\) A1
(ii) \(\overrightarrow {{\text{OA}}} = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right)\), \(\overrightarrow {{\text{OG}}} = \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
2
\end{array}} \right)\)
\(\overrightarrow {{\text{AG}}} = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
since \(\overrightarrow {{\text{AG}}} = 2(\overrightarrow {{\text{MP}}} \times \overrightarrow {{\text{MN}}} )\) AG is perpendicular to MNP R1
(iii) \(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
2
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right)\) M1A1
\(r \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) (accept \( – x + y + z = 3\)) A1
[7 marks]
(d) \(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) A1
\(\left( {\begin{array}{*{20}{c}}
{2 – 2\lambda } \\
{2\lambda } \\
{2\lambda }
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
1 \\
1
\end{array}} \right) = 3\) M1A1
\( – 2 + 2\lambda + 2\lambda + 2\lambda = 3\)
\(\lambda = \frac{5}{6}\) A1
\(r = \left( {\begin{array}{*{20}{c}}
2 \\
0 \\
0
\end{array}} \right) + \frac{5}{6}\left( {\begin{array}{*{20}{c}}
{ – 2} \\
2 \\
2
\end{array}} \right)\) M1
coordinates of point \(\left( {\frac{1}{3},\frac{5}{3},\frac{5}{3}} \right)\) A1
[6 marks]
Total [20 marks]
Examiners report
This was the most successfully answered question in part B, with many candidates achieving full marks. There were a few candidates who misread the question and treated the cube as a unit cube. The most common errors were either algebraic or arithmetic mistakes. A variety of notation forms were seen but in general were used consistently. In a few cases, candidates failed to show all the work or set it properly.