Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 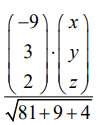
\(=\frac{32}{\sqrt{94}}\)

Question
Consider the three planes
∏1 : 2x – y + z = 4
∏2 : x – 2y + 3z = 5
∏3 : -9x + 3y – 2z = 32
(a) Show that the three planes do not intersect.
(b) (i) Verify that the point P(1 , -2 , 0) lies on both ∏1 and ∏2 .
(ii) Find a vector equation of L, the line of intersection of ∏1 and ∏2 .
(c) Find the distance between L and ∏3 .
▶️Answer/Explanation
Ans:
(a) METHOD 1
attempt to eliminate a variable
obtain a pair of equations in two variables
EITHER
-3x + z = -3 and
-3x + z = 44
OR
-5x + y = -7 and
-5x + y = 40
OR
3x – z = 3 and
3x – z = \(\frac{79}{5}\)
THEN
the two lines are parallel ( – 3 ≠ 44 or – 7 ≠ 40 or 3 ≠ -\(\frac{79}{5}\)
Note: There are other possible pairs of equations in two variables.
To obtain the final R1, at least the initial M1 must have been awarded.
hence the three planes do not intersect
METHOD 2
vector product of the two normals = \(\begin{pmatrix}-1\\-5\\-3\end{pmatrix}\) (or equivalent)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\) (or equivalent)
Note: Award A0 if “r =” is missing. Subsequent marks may still be awarded.
Attempt to substitute (1 + λ, -2 + 5λ, 3λ) in ∏3
-9(1 + λ) + 3(-2+5λ) – 2(3λ) = 32
− 15 = 32, a contradiction
hence the three planes do not intersect
(b) (i) ∏1 : 2 + 2 + 0 = 4 and ∏2 : 1 + 4 + 0 = 5
(ii) METHOD 1
attempt to find the vector product of the two normals
\(\begin{pmatrix}2\\-1 \\1 \end{pmatrix} \times \begin{pmatrix}1\\-2 \\3 \end{pmatrix}\)
\(=\begin{pmatrix}-1\\-5 \\-3 \end{pmatrix}\)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector.
Working for (b)(ii) may be seen in part (a) Method 2. In this case penalize
lack of “r =” only once.
METHOD 2
attempt to eliminate a variable from ∏1 and ∏2
3x – z = 3 OR 3y – 5z = -6 OR 5x – y = 7
Let x = t
substituting x = t in 3x – z = 3 to obtain
z = -3 + 3t and y = 5t – 7 (for all three variables in parametric form)
\(r = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + \lambda \begin{pmatrix}1\\5 \\3 \end{pmatrix}\)
Note: Award A1A0 if “r =” is missing.
Accept any multiple of the direction vector. Accept other position vectors
which satisfy both the planes ∏1 and ∏2 .
(c) METHOD 1
the line connecting L and ∏3 is given by L1
attempt to substitute position and direction vector to form L1
\(s = \begin{pmatrix}1\\-2 \\0 \end{pmatrix} + t \begin{pmatrix}-9\\3 \\-2 \end{pmatrix}\)
substitute (1 – 9t, – 2 + 3t, – 2t) in ∏3
-9(1-9t) + 3(-2+3t) – 2(-2t) = 32
\(94t = 47\Rightarrow t=\frac{1}{2}\)
attempt to find distance between (1, -2,0) and their point \(\begin{pmatrix}-\frac{7}{2}, & -\frac{1}{2}, & -1 \end{pmatrix}\)
\(=\left | \begin{pmatrix}1\\-2 \\0 \end{pmatrix} +\frac{1}{2}\begin{pmatrix}-9\\3 \\-2 \end{pmatrix}-\begin{pmatrix}1\\-2 \\0 \end{pmatrix}\right | = \frac{1}{2}\sqrt{(-9)^{2}+3^{2}+(-2)^{2}}\)
\(=\frac{\sqrt{94}}{2}\)
METHOD 2
unit normal vector equation of ∏3 is given by 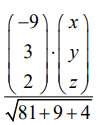
\(=\frac{32}{\sqrt{94}}\)

Question
The points A, B, C have position vectors i + j + 2k , i + 2j + 3k , 3i + k respectively and lie in the plane \(\pi \) .
(a) Find
(i) the area of the triangle ABC;
(ii) the shortest distance from C to the line AB;
(iii) the cartesian equation of the plane \(\pi \) .
The line L passes through the origin and is normal to the plane \(\pi \) , it intersects \(\pi \) at the
point D.
(b) Find
(i) the coordinates of the point D;
(ii) the distance of \(\pi \) from the origin.
▶️Answer/Explanation
Markscheme
(a) (i) METHOD 1
\(\overrightarrow {{\text{AB}}} = \boldsymbol{b} – \boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
1 \\
2 \\
3
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1 \\
1 \\
2
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
1
\end{array}} \right)\) (A1)
\(\overrightarrow {{\text{AC}}} = \boldsymbol{c} – \boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
3 \\
0 \\
1
\end{array}} \right) – \left( {\begin{array}{*{20}{c}}
1 \\
1 \\
2
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
2 \\
{ – 1} \\
{ – 1}
\end{array}} \right)\) (A1)
\(\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{AC}}} = \left| {\begin{array}{*{20}{c}}
\boldsymbol{i}&\boldsymbol{j}&\boldsymbol{k} \\
0&1&1 \\
2&{ – 1}&{ – 1}
\end{array}} \right|\) M1
= i(−1 + 1) − j(0 − 2) + k (0 − 2) (A1)
= 2j − 2k A1
Area of triangle ABC}} \( = \frac{1}{2}\left| {2{\mathbf{j}} – 2{\mathbf{k}}} \right| = {\text{ }}\frac{1}{2}\sqrt 8 \) \(( = \sqrt 2 )\) sq. units M1A1
Note: Allow FT on final A1.
METHOD 2
\(\left| {{\text{AB}}} \right| = \sqrt 2 ,{\text{ }}\left| {{\text{BC}}} \right| = \sqrt {12} ,{\text{ }}\left| {{\text{AC}}} \right| = \sqrt 6 \) A1A1A1
Using cosine rule, e.g. on \({\hat C}\) M1
\(\cos C = \frac{{6 + 12 – 2}}{{2\sqrt {72} }} = \frac{{2\sqrt 2 }}{3}\) A1
\(\therefore {\text{Area }}\Delta {\text{ABC}} = \frac{1}{2}ab\sin C\) M1
\( = \frac{1}{2}\sqrt {12} \sqrt 6 \sin \left( {\arccos \frac{{2\sqrt 2 }}{3}} \right)\)
\( = 3\sqrt 2 \sin \left( {\arccos \frac{{2\sqrt 2 }}{3}} \right){\text{ }}\left( { = \sqrt 2 } \right)\) A1
Note: Allow FT on final A1.
(ii) \({\text{AB}} = \sqrt 2 \) A1
\(\sqrt 2 = \frac{1}{2}{\text{AB}} \times h = \frac{1}{2}\sqrt 2 \times h{\text{ , }}h\) equals the shortest distance (M1)
\( \Rightarrow h = 2\) A1
(iii) METHOD 1
(\pi \) has form \(r \cdot \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
{ – 2}
\end{array}} \right) = d\) (M1)
Since (1, 1, 2) is on the plane
\(d = \left( {\begin{array}{*{20}{c}}
1 \\
1 \\
2
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
{ – 2}
\end{array}} \right) = 2 – 4 = -2\) M1A1
Hence \(r \cdot \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
{ – 2}
\end{array}} \right) = – 2\)
\(2y – 2z = – 2{\text{ (or }}y – z = – 1)\) A1
METHOD 2
\(r = \left( {\begin{array}{*{20}{c}}
1 \\
1 \\
2
\end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
1
\end{array}} \right) + \mu \left( {\begin{array}{*{20}{c}}
2 \\
{ – 1} \\
{ – 1}
\end{array}} \right)\) (M1)
\(x = 1 + 2\mu \) (i)
\(y = 1 + \lambda – \mu \) (ii)
\(z = 2 + \lambda – \mu \) (iii) A1
Note: Award A1 for all three correct, A0 otherwise.
From (i) \(\mu = \frac{{x – 1}}{2}\)
substitute in (ii) \(y = 1 + \lambda – \left( {\frac{{x – 1}}{2}} \right)\)
\( \Rightarrow \lambda = y – 1 + \left( {\frac{{x – 1}}{2}} \right)\)
substitute \(\lambda \) and \(\mu \) in (iii) M1
\( \Rightarrow z = 2 + y – 1 + \left( {\frac{{x – 1}}{2}} \right) – \left( {\frac{{x – 1}}{2}} \right)\)
\( \Rightarrow y – z = – 1\) A1
[14 marks]
(b) (i) The equation of OD is
\(r = \lambda \left( {\begin{array}{*{20}{c}}
0 \\
2 \\
{ – 2}
\end{array}} \right)\), \(\left( {{\text{or }}r = \lambda \left( {\begin{array}{*{20}{c}}
0 \\
1 \\
{ – 1}
\end{array}} \right)} \right)\) M1
This meets \(\pi \) where
\(2\lambda + 2\lambda = – 1\) (M1)
\(\lambda = – \frac{1}{4}\) A1
Coordinates of D are \(\left( {0, – \frac{1}{2},\frac{1}{2}} \right)\) A1
(ii) \(\left| {\overrightarrow {{\text{OD}}} } \right| = \sqrt {0 + {{\left( { – \frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{1}{{\sqrt 2 }}\) (M1)A1
[6 marks]
Total [20 marks]
Examiners report
It was disappointing to see that a number of candidates did not appear to be well prepared for this question and made no progress at all. There were a number of schools where no candidate made any appreciable progress with the question. A good number of students, however, were successful with part (a) (i). A good number of candidates were also successful with part a (ii) but few realised that the shortest distance was the height of the triangle. Candidates used a variety of methods to answer (a) (iii) but again a reasonable number of correct answers were seen. Candidates also had a reasonable degree of success with part (b), with a respectable number of correct answers seen.
Question
Consider the plane with equation \(4x – 2y – z = 1\) and the line given by the parametric equations
\(x = 3 – 2\lambda \)
\(y = (2k – 1) + \lambda \)
\(z = – 1 + k\lambda .\)
Given that the line is perpendicular to the plane, find
(a) the value of k;
(b) the coordinates of the point of intersection of the line and the plane.
▶️Answer/Explanation
Markscheme
(a) \(\boldsymbol{a} = \left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
{ – 1}
\end{array}} \right) \bot \) to the plane \(\boldsymbol{e} = \left( {\begin{array}{*{20}{c}}
{ – 2} \\
1 \\
k
\end{array}} \right)\) is parallel to the line (A1)(A1)
Note: Award A1 for each correct vector written down, even if not identified.
line \( \bot \) plane \( \Rightarrow \) \(\boldsymbol{e}\) parallel to \(\boldsymbol{a}\)
since \(\left( {\begin{array}{*{20}{c}}
4 \\
{ – 2} \\
{ – 1}
\end{array}} \right) = t\left( {\begin{array}{*{20}{c}}
{ – 2} \\
1 \\
k
\end{array}} \right) \Rightarrow k = \frac{1}{2}\) (M1)A1
(b) \(4(3 – 2\lambda ) – 2\lambda – \left( { – 1 + \frac{1}{2}\lambda } \right) = 1\) (M1)(A1)
Note: FT their value of k as far as possible.
\(\lambda = \frac{8}{7}\) A1
\({\text{P}}\left( {\frac{5}{7},\frac{8}{7}, – \frac{3}{7}} \right)\) A1
[8 marks]
Examiners report
Solutions to this question were often disappointing. In (a), some candidates found the value of k, incorrectly, by taking the scalar product of the normal vector to the plane and the direction of the line. Such candidates benefitted partially from follow through in (b) but not fully because their line turned out to be parallel to the plane and did not intersect it.
Question
Consider the points \({\text{A(1, 0, 0)}}\), \({\text{B(2, 2, 2)}}\) and \({\text{C(0, 2, 1)}}\).
A third plane \({\Pi _3}\) is defined by the Cartesian equation \(16x + \alpha y – 3z = \beta \).
a.Find the vector \(\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CB}}} \).[4]
b.Find an exact value for the area of the triangle ABC.[3]
c.Show that the Cartesian equation of the plane \({\Pi _1}\), containing the triangle ABC, is \(2x + 3y – 4z = 2\).[3]
d.A second plane \({\Pi _2}\) is defined by the Cartesian equation \({\Pi _2}:4x – y – z = 4\). \({L_1}\) is the line of intersection of the planes \({\Pi _1}\) and \({\Pi _2}\).
Find a vector equation for \({L_1}\).[5]
e.Find the value of \(\alpha \) if all three planes contain \({L_1}\).[3]
f.Find conditions on \(\alpha \) and \(\beta \) if the plane \({\Pi _3}\) does not intersect with \({L_1}\).[2]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\rm{CA}}} = \left( \begin{array}{c}1\\ – 2\\ – 1\end{array} \right)\) (A1)
\(\overrightarrow {{\rm{CB}}} = \left( \begin{array}{c}2\\0\\1\end{array} \right)\) (A1)
Note: If \(\overrightarrow {{\text{AC}}} \) and \(\overrightarrow {{\text{BC}}} \) found correctly award (A1) (A0).
\(\overrightarrow {{\rm{CA}}} \times \overrightarrow {{\rm{CB}}} = \left| {\begin{array}{*{20}{c}}i&j&k\\1&{ – 2}&{ – 1}\\2&0&1\end{array}} \right|\) (M1)
\(\left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right)\) A1
[4 marks]
METHOD 1
\(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CB}}} } \right|\) (M1)
\( = \frac{1}{2}\sqrt {{{( – 2)}^2} + {{( – 3)}^2} + {4^2}} \) (A1)
\( = \frac{{\sqrt {29} }}{2}\) A1
METHOD 2
attempt to apply \(\frac{1}{2}\left| {{\text{CA}}} \right|\left| {{\text{CB}}} \right|\sin C\) (M1)
\({\text{CA.CB}} = \sqrt 5 .\sqrt 6 \cos C \Rightarrow \cos C = \frac{1}{{\sqrt {30} }} \Rightarrow \sin C = \frac{{\sqrt {29} }}{{\sqrt {30} }}\) (A1)
\({\text{area}} = \frac{{\sqrt {29} }}{2}\) A1
[3 marks]
METHOD 1
r.\(\left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right) = \left( \begin{array}{l}1\\0\\0\end{array} \right) \bullet \left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right)\) M1A1
\( \Rightarrow – 2x – 3y + 4z = – 2\) A1
\( \Rightarrow 2x + 3y – 4z = 2\) AG
METHOD 2
\( – 2x – 3y + 4z = d\)
substituting a point in the plane M1A1
\({\text{d}} = – 2\) A1
\( \Rightarrow – 2x – 3y + 4z = – 2\)
\( \Rightarrow 2x + 3y – 4z = 2\) AG
Note: Accept verification that all 3 vertices of the triangle lie on the given plane.
[3 marks]
METHOD 1
\(\left| {\begin{array}{*{20}{c}}{\mathbf{i}}&{\mathbf{j}}&{\mathbf{k}}\\2&3&{ – 4}\\4&{ – 1}&{ – 1}\end{array}} \right| = \left( \begin{array}{c} – 7\\ – 14\\ – 14\end{array} \right)\) M1A1
\({\mathbf{n}} = \left( \begin{array}{l}1\\2\\2\end{array} \right)\)
\(z = 0 \Rightarrow y = 0,{\text{ }}x = 1\) (M1)(A1)
\({L_1}:{\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + \lambda \left( \begin{array}{l}1\\2\\2\end{array} \right)\) A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
METHOD 2
eliminate 1 of the variables, eg x M1
\( – 7y + 7z = 0\) (A1)
introduce a parameter M1
\( \Rightarrow z = \lambda \),
\(y = \lambda {\text{, }}x = 1 + \frac{\lambda }{2}\) (A1)
\({\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + \lambda \left( \begin{array}{l}1\\2\\2\end{array} \right)\) or equivalent A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
METHOD 3
\(z = t\) M1
write x and y in terms of \(t \Rightarrow 4x – y = 4 + t,{\text{ }}2x + 3y = 2 + 4t\) or equivalent A1
attempt to eliminate x or y M1
\(x,{\text{ }}y,{\text{ }}z\) expressed in parameters
\( \Rightarrow z = t\),
\(y = t,{\text{ }}x = 1 + \frac{t}{2}\) A1
\({\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + t \left( \begin{array}{l}1\\2\\2\end{array} \right)\) or equivalent A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
[5 marks]
METHOD 1
direction of the line is perpendicular to the normal of the plane
\(\left( \begin{array}{c}16\\\alpha \\ – 3\end{array} \right) \bullet \left( \begin{array}{l}1\\2\\2\end{array} \right) = 0\) M1A1
\(16 + 2\alpha – 6 = 0 \Rightarrow \alpha = – 5\) A1
METHOD 2
solving line/plane simultaneously
\(16(1 + \lambda ) + 2\alpha \lambda – 6\lambda = \beta \) M1A1
\(16 + (10 + 2\alpha )\lambda = \beta \)
\( \Rightarrow \alpha = – 5\) A1
METHOD 3
\(\left| {\begin{array}{*{20}{c}}2&3&{ – 4}\\4&{ – 1}&{ – 1}\\{16}&\alpha &{ – 3}\end{array}} \right| = 0\) M1
\(2(3 + \alpha ) – 3( – 12 + 16) – 4(4\alpha + 16) = 0\) A1
\( \Rightarrow \alpha = – 5\) A1
METHOD 4
attempt to use row reduction on augmented matrix M1
to obtain \(\left( {\begin{array}{*{20}{c}}2&3&{ – 4}\\0&{ – 1}&1\\0&0&{\alpha + 5}\end{array}\left| \begin{array}{c}2\\0\\\beta – 16\end{array} \right.} \right)\) A1
\( \Rightarrow \alpha = – 5\) A1
[3 marks]
\(\alpha = – 5\) A1
\(\beta \ne 16\) A1
[2 marks]
Question
Consider the points \({\text{A(1, 0, 0)}}\), \({\text{B(2, 2, 2)}}\) and \({\text{C(0, 2, 1)}}\).
A third plane \({\Pi _3}\) is defined by the Cartesian equation \(16x + \alpha y – 3z = \beta \).
a.Find the vector \(\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CB}}} \).[4]
b.Find an exact value for the area of the triangle ABC.[3]
c.Show that the Cartesian equation of the plane \({\Pi _1}\), containing the triangle ABC, is \(2x + 3y – 4z = 2\).[3]
d.A second plane \({\Pi _2}\) is defined by the Cartesian equation \({\Pi _2}:4x – y – z = 4\). \({L_1}\) is the line of intersection of the planes \({\Pi _1}\) and \({\Pi _2}\).
Find a vector equation for \({L_1}\).[5]
e.Find the value of \(\alpha \) if all three planes contain \({L_1}\).[3]
f.Find conditions on \(\alpha \) and \(\beta \) if the plane \({\Pi _3}\) does not intersect with \({L_1}\).[2]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\rm{CA}}} = \left( \begin{array}{c}1\\ – 2\\ – 1\end{array} \right)\) (A1)
\(\overrightarrow {{\rm{CB}}} = \left( \begin{array}{c}2\\0\\1\end{array} \right)\) (A1)
Note: If \(\overrightarrow {{\text{AC}}} \) and \(\overrightarrow {{\text{BC}}} \) found correctly award (A1) (A0).
\(\overrightarrow {{\rm{CA}}} \times \overrightarrow {{\rm{CB}}} = \left| {\begin{array}{*{20}{c}}i&j&k\\1&{ – 2}&{ – 1}\\2&0&1\end{array}} \right|\) (M1)
\(\left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right)\) A1
[4 marks]
METHOD 1
\(\frac{1}{2}\left| {\overrightarrow {{\text{CA}}} \times \overrightarrow {{\text{CB}}} } \right|\) (M1)
\( = \frac{1}{2}\sqrt {{{( – 2)}^2} + {{( – 3)}^2} + {4^2}} \) (A1)
\( = \frac{{\sqrt {29} }}{2}\) A1
METHOD 2
attempt to apply \(\frac{1}{2}\left| {{\text{CA}}} \right|\left| {{\text{CB}}} \right|\sin C\) (M1)
\({\text{CA.CB}} = \sqrt 5 .\sqrt 6 \cos C \Rightarrow \cos C = \frac{1}{{\sqrt {30} }} \Rightarrow \sin C = \frac{{\sqrt {29} }}{{\sqrt {30} }}\) (A1)
\({\text{area}} = \frac{{\sqrt {29} }}{2}\) A1
[3 marks]
METHOD 1
r.\(\left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right) = \left( \begin{array}{l}1\\0\\0\end{array} \right) \bullet \left( \begin{array}{c} – 2\\ – 3\\4\end{array} \right)\) M1A1
\( \Rightarrow – 2x – 3y + 4z = – 2\) A1
\( \Rightarrow 2x + 3y – 4z = 2\) AG
METHOD 2
\( – 2x – 3y + 4z = d\)
substituting a point in the plane M1A1
\({\text{d}} = – 2\) A1
\( \Rightarrow – 2x – 3y + 4z = – 2\)
\( \Rightarrow 2x + 3y – 4z = 2\) AG
Note: Accept verification that all 3 vertices of the triangle lie on the given plane.
[3 marks]
METHOD 1
\(\left| {\begin{array}{*{20}{c}}{\mathbf{i}}&{\mathbf{j}}&{\mathbf{k}}\\2&3&{ – 4}\\4&{ – 1}&{ – 1}\end{array}} \right| = \left( \begin{array}{c} – 7\\ – 14\\ – 14\end{array} \right)\) M1A1
\({\mathbf{n}} = \left( \begin{array}{l}1\\2\\2\end{array} \right)\)
\(z = 0 \Rightarrow y = 0,{\text{ }}x = 1\) (M1)(A1)
\({L_1}:{\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + \lambda \left( \begin{array}{l}1\\2\\2\end{array} \right)\) A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
METHOD 2
eliminate 1 of the variables, eg x M1
\( – 7y + 7z = 0\) (A1)
introduce a parameter M1
\( \Rightarrow z = \lambda \),
\(y = \lambda {\text{, }}x = 1 + \frac{\lambda }{2}\) (A1)
\({\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + \lambda \left( \begin{array}{l}1\\2\\2\end{array} \right)\) or equivalent A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
METHOD 3
\(z = t\) M1
write x and y in terms of \(t \Rightarrow 4x – y = 4 + t,{\text{ }}2x + 3y = 2 + 4t\) or equivalent A1
attempt to eliminate x or y M1
\(x,{\text{ }}y,{\text{ }}z\) expressed in parameters
\( \Rightarrow z = t\),
\(y = t,{\text{ }}x = 1 + \frac{t}{2}\) A1
\({\mathbf{r}} = \left( \begin{array}{l}1\\0\\0\end{array} \right) + t \left( \begin{array}{l}1\\2\\2\end{array} \right)\) or equivalent A1
Note: Do not award the final A1 if \(\mathbf{r} =\) is not seen.
[5 marks]
METHOD 1
direction of the line is perpendicular to the normal of the plane
\(\left( \begin{array}{c}16\\\alpha \\ – 3\end{array} \right) \bullet \left( \begin{array}{l}1\\2\\2\end{array} \right) = 0\) M1A1
\(16 + 2\alpha – 6 = 0 \Rightarrow \alpha = – 5\) A1
METHOD 2
solving line/plane simultaneously
\(16(1 + \lambda ) + 2\alpha \lambda – 6\lambda = \beta \) M1A1
\(16 + (10 + 2\alpha )\lambda = \beta \)
\( \Rightarrow \alpha = – 5\) A1
METHOD 3
\(\left| {\begin{array}{*{20}{c}}2&3&{ – 4}\\4&{ – 1}&{ – 1}\\{16}&\alpha &{ – 3}\end{array}} \right| = 0\) M1
\(2(3 + \alpha ) – 3( – 12 + 16) – 4(4\alpha + 16) = 0\) A1
\( \Rightarrow \alpha = – 5\) A1
METHOD 4
attempt to use row reduction on augmented matrix M1
to obtain \(\left( {\begin{array}{*{20}{c}}2&3&{ – 4}\\0&{ – 1}&1\\0&0&{\alpha + 5}\end{array}\left| \begin{array}{c}2\\0\\\beta – 16\end{array} \right.} \right)\) A1
\( \Rightarrow \alpha = – 5\) A1
[3 marks]
\(\alpha = – 5\) A1
\(\beta \ne 16\) A1
[2 marks]
Question
a.Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square.
Find the coordinates of M, the mid-point of [OB].[1]
Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]
Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
(i) Find the angle \({\rm{O\hat DA}}\).
(ii) State what this tells you about the solid OABCDE.[6]
▶️Answer/Explanation
Markscheme
\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
Question
a.Show that the points \({\text{O}}(0,{\text{ }}0,{\text{ }}0)\), \({\text{ A}}(6,{\text{ }}0,{\text{ }}0)\), \({\text{B}}({6,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12} })\), \({\text{C}}({0,{\text{ }}- \sqrt {24} ,{\text{ }}\sqrt {12}})\) form a square.[3]
Find the coordinates of M, the mid-point of [OB].[1]
Show that an equation of the plane \({\mathit{\Pi }}\), containing the square OABC, is \(y + \sqrt 2 z = 0\).[3]
Find a vector equation of the line \(L\), through M, perpendicular to the plane \({\mathit{\Pi }}\).[3]
Find the coordinates of D, the point of intersection of the line \(L\) with the plane whose equation is \(y = 0\).[3]
Find the coordinates of E, the reflection of the point D in the plane \({\mathit{\Pi }}\).[3]
(i) Find the angle \({\rm{O\hat DA}}\).
(ii) State what this tells you about the solid OABCDE.[6]
▶️Answer/Explanation
Markscheme
\(\left| {\overrightarrow {{\text{OA}}} } \right| = \left| {\overrightarrow {{\text{CB}}} } \right| = \left| {\overrightarrow {{\text{OC}}} } \right| = \left| {\overrightarrow {{\text{AB}}} } \right| = 6\) (therefore a rhombus) A1A1
Note: Award A1 for two correct lengths, A2 for all four.
Note: Award A1A0 for \(\overrightarrow {{\rm{OA}}} = \overrightarrow {{\rm{CB}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{ or \,\,} } \overrightarrow {{\rm{OC}}} = \overrightarrow {A{\rm{B}}} = \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right)\) if no magnitudes are shown.
\(\overrightarrow {{\rm{OA}}}\,\, {\rm{ g}}\overrightarrow {{\rm{OC}}} = \left( \begin{array}{l}6\\0\\0\end{array} \right){\rm{g}}\left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = 0 \) (therefore a square) A1
Note: Other arguments are possible with a minimum of three conditions.
[3 marks]
\({\text{M}}\left( {3,{\text{ }} – \frac{{\sqrt {24} }}{2},{\text{ }}\frac{{\sqrt {12} }}{2}} \right)\left( { = \left( {3,{\text{ }} – \sqrt 6 ,{\text{ }}\sqrt 3 } \right)} \right)\) A1
[1 mark]
METHOD 1
\(\overrightarrow {{\text{OA}}} \times \overrightarrow {{\text{OC}}} = \)\(\left( \begin{array}{l}6\\0\\0\end{array} \right) \times \left( \begin{array}{c}0\\ – \sqrt {24} \\\sqrt {12} \end{array} \right) = \left( \begin{array}{c}0\\ – 6\sqrt {12} \\ – 6\sqrt {24} \end{array} \right)\left( { = \left( \begin{array}{c}0\\ – 12\sqrt 3 \\ – 12\sqrt 6 \end{array} \right)} \right)\) M1A1
Note: Candidates may use other pairs of vectors.
equation of plane is \( – 6\sqrt {12} y – 6\sqrt {24} z = d\)
any valid method showing that \(d = 0\) M1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
METHOD 2
equation of plane is \(ax + by + cz = d\)
substituting O to find \(d = 0\) (M1)
substituting two points (A, B, C or M) M1
eg
\(6a = 0,{\text{ }} – \sqrt {24} b + \sqrt {12} c = 0\) A1
\(\mathit{\Pi} :y+\sqrt{2z}=0\) AG
[3 marks]
\(\boldsymbol{r} = \left( \begin{array}{c}3\\ – \sqrt 6 \\\sqrt 3 \end{array} \right) + \lambda \left( \begin{array}{l}0\\1\\\sqrt 2 \end{array} \right)\) A1A1A1
Note: Award A1 for r = , A1A1 for two correct vectors.
[3 marks]
Using \(y = 0\) to find \(\lambda \) M1
Substitute their \(\lambda \) into their equation from part (d) M1
D has coordinates \(\left( {{\text{3, 0, 3}}\sqrt 3 } \right)\) A1
[3 marks]
\(\lambda \) for point E is the negative of the \(\lambda \) for point D (M1)
Note: Other possible methods may be seen.
E has coordinates \(\left( {{\text{3, }} – 2\sqrt 6 ,{\text{ }} – \sqrt 3 } \right)\) A1A1
Note: Award A1 for each of the y and z coordinates.
[3 marks]
(i) \(\overrightarrow {{\text{DA}}} {\text{ g}}\overrightarrow {{\text{DO}}} = \)\(\left( \begin{array}{c}3\\0\\ – 3\sqrt 3 \end{array} \right){\rm{g}}\left( \begin{array}{c} – 3\\0\\ – 3\sqrt 3 \end{array} \right) = 18\) M1A1
\(\cos {\rm{O\hat DA}} = \frac{{18}}{{\sqrt {36} \sqrt {36} }} = \frac{1}{2}\) M1
hence \({\rm{O\hat DA}} = 60^\circ \) A1
Note: Accept method showing OAD is equilateral.
(ii) OABCDE is a regular octahedron (accept equivalent description) A2
Note: A2 for saying it is made up of 8 equilateral triangles
Award A1 for two pyramids, A1 for equilateral triangles.
(can be either stated or shown in a sketch – but there must be clear indication the triangles are equilateral)
[6 marks]
Question
Consider the plane \({\mathit{\Pi} _1}\), parallel to both lines \({L_1}\) and \({L_2}\). Point C lies in the plane \({\mathit{\Pi} _1}\).
The line \({L_3}\) has vector equation \(\boldsymbol{r} = \left( \begin{array}{l}3\\0\\1\end{array} \right) + \lambda \left( \begin{array}{c}k\\1\\ – 1\end{array} \right)\).
The plane \({\mathit{\Pi} _2}\) has Cartesian equation \(x + y = 12\).
The angle between the line \({L_3}\) and the plane \({\mathit{\Pi} _2}\) is 60°.
a.Given the points A(1, 0, 4), B(2, 3, −1) and C(0, 1, − 2) , find the vector equation of the line \({L_1}\) passing through the points A and B.[2]
The line \({L_2}\) has Cartesian equation \(\frac{{x – 1}}{3} = \frac{{y + 2}}{1} = \frac{{z – 1}}{{ – 2}}\).
Show that \({L_1}\) and \({L_2}\) are skew lines.[5]
Find the Cartesian equation of the plane \({\Pi _1}\).[4]
(i) Find the value of \(k\).
(ii) Find the point of intersection P of the line \({L_3}\) and the plane \({\mathit{\Pi} _2}\).[7]
▶️Answer/Explanation
Markscheme
direction vector \(\overrightarrow {{\rm{AB}}} = \left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or \(\overrightarrow {{\rm{BA}}} = \left( \begin{array}{c} – 1\\ – 3\\5\end{array} \right)\) A1
\(\boldsymbol{r} = \left( \begin{array}{l}1\\0\\4\end{array} \right) + t\left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or \(\boldsymbol{r} = \left( \begin{array}{c}2\\3\\ – 1\end{array} \right) + t\left( \begin{array}{c}1\\3\\ – 5\end{array} \right)\) or equivalent A1
Note: Do not award final A1 unless ‘\(\boldsymbol{r} = {\text{K}}\)’ (or equivalent) seen.
Allow FT on direction vector for final A1.
[2 marks]
both lines expressed in parametric form:
\({L_1}\):
\(x = 1 + t\)
\(y = 3t\)
\(z = 4 – 5t\)
\({L_2}\):
\(x = 1 + 3s\)
\(y = – 2 + s\) M1A1
\(z = – 2s + 1\)
Notes: Award M1 for an attempt to convert \({L_2}\) from Cartesian to parametric form.
Award A1 for correct parametric equations for \({L_1}\) and \({L_2}\).
Allow M1A1 at this stage if same parameter is used in both lines.
attempt to solve simultaneously for x and y: M1
\(1 + t = 1 + 3s\)
\(3t = – 2 + s\)
\(t = – \frac{3}{4},{\text{ }}s = – \frac{1}{4}\) A1
substituting both values back into z values respectively gives \(z = \frac{{31}}{4}\)
and \(z = \frac{3}{2}\) so a contradiction R1
therefore \({L_1}\) and \({L_1}\) are skew lines AG
[5 marks]
finding the cross product:
\(\left( \begin{array}{c}1\\3\\ – 5\end{array} \right) \times \left( \begin{array}{c}3\\1\\ – 2\end{array} \right)\) (M1)
= – i – 13j – 8k A1
Note: Accept i + 13j + 8k
\( – 1(0) – 13(1) – 8( – 2) = 3\) (M1)
\( \Rightarrow – x – 13y – 8z = 3\) or equivalent A1
[4 marks]
(i) \((\cos \theta = )\frac{{\left( \begin{array}{c}k\\1\\ – 1\end{array} \right) \bullet \left( \begin{array}{l}1\\1\\0\end{array} \right)}}{{\sqrt {{k^2} + 1 + 1} \times \sqrt {1 + 1} }}\) M1
Note: Award M1 for an attempt to use angle between two vectors formula.
\(\frac{{\sqrt 3 }}{2} = \frac{{k + 1}}{{\sqrt {2({k^2} + 2)} }}\) A1
obtaining the quadratic equation
\(4{(k + 1)^2} = 6({k^2} + 2)\) M1
\({k^2} – 4k + 4 = 0\)
\({(k – 2)^2} = 0\)
\(k = 2\) A1
Note: Award M1A0M1A0 if \(\cos 60^\circ \) is used \((k = 0{\text{ or }}k = – 4)\).
(ii) \(r = \left( \begin{array}{l}3\\0\\1\end{array} \right) + \lambda \left( \begin{array}{c}2\\1\\ – 1\end{array} \right)\)
substituting into the equation of the plane \({\Pi _2}\):
\(3 + 2\lambda + \lambda = 12\) M1
\(\lambda = 3\) A1
point P has the coordinates:
(9, 3, –2) A1
Notes: Accept 9i + 3j – 2k and \(\left( \begin{array}{l}9\\3\\- 2\end{array} \right)\).
Do not allow FT if two values found for k.
[7 marks]
Question
Two planes have equations
\[{\Pi _1}:{\text{ }}4x + y + z = 8{\text{ and }}{\Pi _2}:{\text{ }}4x + 3y – z = 0\]
Let \(L\) be the line of intersection of the two planes.
B is the point on \({\Pi _1}\) with coordinates \((a,{\text{ }}b,{\text{ }}1)\).
The point P lies on \(L\) and \({\rm{A\hat BP}} = 45^\circ \).
a.Find the cosine of the angle between the two planes in the form \(\sqrt {\frac{p}{q}} \) where \(p,{\text{ }}q \in \mathbb{Z}\).[4]
(i) Show that \(L\) has direction \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
(ii) Show that the point \({\text{A }}(1,{\text{ }}0,{\text{ }}4)\) lies on both planes.
(iii) Write down a vector equation of \(L\).[6]
Given the vector \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(L\) find the value of \(a\) and the value of \(b\).[5]
Show that \({\text{AB}} = 3\sqrt 2 \).[1]
Find the coordinates of the two possible positions of \(P\).[5]
▶️Answer/Explanation
Markscheme
Note: Throughout the question condone vectors written horizontally.
angle between planes is equal to the angles between the normal to the planes (M1)
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = 18\) (A1)
let \(\theta \) be the angle between the normal to the planes
\(\cos \theta = \frac{{18}}{{\sqrt {18} \sqrt {26} }} = \sqrt {\frac{{18}}{{26}}} {\text{ }}\left( {{\text{or equivalent, for example }}\sqrt {\frac{{324}}{{468}}} {\text{ or }}\sqrt {\frac{9}{{13}}} } \right)\) M1A1
[4 marks]
Note: Throughout the question condone vectors written horizontally.
(i) METHOD 1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right)\) M1A1
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
Note: Allow any equivalent wording or \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = 4\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\), do not allow \(\left( {\begin{array}{*{20}{c}} { – 4} \\ 8 \\ 8 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\).
METHOD 2
let \(z = t\) (or equivalent)
solve simultaneously to get M1
\(y = t – 4,{\text{ }}x = 3 – 0.5t\) A1
hence direction vector is \(\left( {\begin{array}{*{20}{c}} { – 0.5} \\ 1 \\ 1 \end{array}} \right)\)
which is a multiple of \(\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) R1AG
METHOD 3
\(\left( {\begin{array}{*{20}{c}} 4 \\ 1 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 2 + 2 = 0\) M1A1
\(\left( {\begin{array}{*{20}{c}} 4 \\ 3 \\ { – 1} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = – 4 + 6 – 2 = 0\) A1
Note: If only one scalar product is found award M0A0A0.
(ii) \({\Pi _1}:{\text{ }}4 + 0 + 4 = 8\) and \({\Pi _2}:{\text{ }}4 + 0 – 4 = 0\) R1
(iii) r \( = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) A1A1
Note: A1 for “r \( = \)” and a correct point on the line, A1 for a parameter and a correct direction vector.
[6 marks]
Note: Throughout the question condone vectors written horizontally.
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 4 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right)\) (A1)
\(\left( {\begin{array}{*{20}{c}} {a – 1} \\ b \\ { – 3} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\) M1
Note: Award M0 for \(\left( {\begin{array}{*{20}{c}} a \\ b \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right) = 0\).
\( – a + 1 + 2b – 6 = 0 \Rightarrow a – 2b = – 5\) A1
lies on \({\Pi _1}\) so \(4a + b + 1 = 8 \Rightarrow 4a + b = 7\) M1
\(a = 1,{\text{ }}b = 3\) A1
[5 marks]
Note: Throughout the question condone vectors written horizontally.
\({\text{AB}} = \sqrt {{0^2} + {3^2} + {{( – 3)}^2}} = 3\sqrt 2 \) M1AG
[1 mark]
Note: Throughout the question condone vectors written horizontally.
METHOD 1
\(\left| {\overrightarrow {{\text{AB}}} } \right| = \left| {\overrightarrow {{\text{AP}}} } \right| = 3\sqrt 2 \) (M1)
\(\overrightarrow {{\text{AP}}} = t\left( {\begin{array}{*{20}{c}} { – 1} \\ 2 \\ 2 \end{array}} \right)\) (A1)
\(\left| {3t} \right| = 3\sqrt 2 \Rightarrow t = \pm \sqrt 2 \) (M1)A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
[5 marks]
METHOD 2
let P have coordinates \((1 – \lambda ,{\text{ }}2\lambda ,{\text{ }}4 + 2\lambda )\) M1
\(\overrightarrow {{\text{BA}}} = \left( {\begin{array}{*{20}{c}} 0 \\ { – 3} \\ 3 \end{array}} \right),{\text{ }}\overrightarrow {{\text{BP}}} = \left( {\begin{array}{*{20}{c}} { – \lambda } \\ {2\lambda – 3} \\ {3 + 2\lambda } \end{array}} \right)\) A1
\(\cos 45^\circ = \frac{{\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} }}{{\left| {{\text{BA}}} \right|\left| {{\text{BP}}} \right|}}\) M1
Note: Award M1 even if AB rather than BA is used in the scalar product.
\(\overrightarrow {{\text{BA}}} \bullet \overrightarrow {{\text{BP}}} = 18\)
\(\frac{1}{{\sqrt 2 }} = \frac{{18}}{{\sqrt {18} \sqrt {9{\lambda ^2} + 18} }}\)
\(\lambda = \pm \sqrt 2 \) A1
\({\text{P}}\left( {1 – \sqrt 2 ,{\text{ }}2\sqrt 2 ,{\text{ }}4 + 2\sqrt 2 } \right)\) and \(\left( {1 + \sqrt 2 ,{\text{ }} – 2\sqrt 2 ,{\text{ }}4 – 2\sqrt 2 } \right)\) A1
Note: Accept answers given as position vectors.
[5 marks]
Question
The following system of equations represents three planes in space.
\[x + 3y + z = – 1\]
\[x + 2y – 2z = 15\]
\[2x + y – z = 6\]
Find the coordinates of the point of intersection of the three planes.
▶️Answer/Explanation
Markscheme
EITHER
eliminating a variable, \(x\), for example to obtain \(y + 3z = – 16\) and \( – 5y – 3z = 8\) M1A1
attempting to find the value of one variable M1
point of intersection is \(( – 1,{\text{ }}2,{\text{ }} – 6)\) A1A1A1
OR
attempting row reduction of relevant matrix, eg.  M1
M1
correct matrix with two zeroes in a column, eg.  A1
A1
further attempt at reduction M1
point of intersection is \(( – 1,{\text{ }}2,{\text{ }} – 6)\) A1A1A1
Note: Allow solution expressed as \(x = – 1,{\text{ }}y = 2,{\text{ }}z = – 6\) for final A marks.
[6 marks]
Examiners report
This provided a generally easy start for many candidates. Most successful candidates obtained their answer through row reduction of a suitable matrix. Those choosing an alternative method often made slips in their algebra.
Question
A line \(L\) has equation \(\frac{{x – 2}}{p} = \frac{{y – q}}{2} = z – 1\) where \(p,{\text{ }}q \in \mathbb{R}\).
A plane \(\Pi \) has equation \(x + y + 3z = 9\).
Consider the different case where the acute angle between \(L\) and \(\Pi \) is \(\theta \)
where \(\theta = \arcsin \left( {\frac{1}{{\sqrt {11} }}} \right)\).
Show that \(L\) is not perpendicular to \(\Pi \).
Given that \(L\) lies in the plane \(\Pi \), find the value of \(p\) and the value of \(q\).
(i) Show that \(p = – 2\).
(ii) If \(L\) intersects \(\Pi \) at \(z = – 1\), find the value of \(q\).
▶️Answer/Explanation
Markscheme
EITHER
n \( = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 3 \end{array}} \right)\) and d \( = \left( {\begin{array}{*{20}{c}} p \\ 2 \\ 1 \end{array}} \right)\) A1A1
and n \( \ne \) kd R1
OR
n \( \times \) d \( = \left( {\begin{array}{*{20}{c}} { – 5} \\ {3p – 1} \\ {2 – p} \end{array}} \right)\) M1A1
the vector product is non-zero for \(p \in \mathbb{R}\) R1
THEN
\(L\) is not perpendicular to \(\Pi \) AG
[3 marks]
METHOD 1
\((2 + p\lambda ) + (q + 2\lambda ) + 3(1 + \lambda ) = 9\) M1
\((q + 5) + (p + 5)\lambda = 9\) (A1)
\(p = – 5\) and \(q = 4\) A1A1
METHOD 2
direction vector of line is perpendicular to plane, so
\(\left( {\begin{array}{*{20}{c}} p \\ 2 \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 3 \end{array}} \right) = 0\) M1
\(p = – 5\) A1
\((2,{\text{ }}q,{\text{ }}1)\) is common to both \(L\) and \(\Pi \)
either \(\left( {\begin{array}{*{20}{c}} 2 \\ q \\ 1 \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 3 \end{array}} \right) = 9\) or by substituting into \(x + y + 3z = 9\) M1
\(q = 4\) A1
[4 marks]
(i) METHOD 1
\(\alpha \) is the acute angle between n and L
if \(\sin \theta = \frac{1}{{\sqrt {11} }}\) then \(\cos \alpha = \frac{1}{{\sqrt {11} }}\) (M1)(A1)
attempting to use \(\cos \alpha = \frac{{n \bullet d}}{{\left| n \right|\left| d \right|}}\) or \(\sin \alpha = \frac{{n \bullet d}}{{\left| n \right|\left| d \right|}}\) M1
\(\frac{{p + 5}}{{\sqrt {11} \times \sqrt {{p^2} + 5} }} = \frac{1}{{\sqrt {11} }}\) A1A1
\({(p + 5)^2} = {p^2} + 5\) M1
\(10p = – 20\) (or equivalent) A1
\(p = – 2\) AG
METHOD 2
\(\alpha \) is the angle between n and L
if \(\sin \theta = \frac{1}{{\sqrt {11} }}\) then \(\sin \alpha = \frac{{\sqrt {10} }}{{\sqrt {11} }}\) (M1)A1
attempting to use \(\sin \alpha = \frac{{\left| {n \times d} \right|}}{{\left| n \right|\left| d \right|}}\) M1
\(\frac{{\sqrt {{{( – 5)}^2} + {{(3p – 1)}^2} + {{(2 – p)}^2}} }}{{\sqrt {11} \times \sqrt {{p^2} + 5} }} = \frac{{\sqrt {10} }}{{\sqrt {11} }}\) A1A1
\({p^2} – p + 3 = {p^2} + 5\) M1
\( – p + 3 = 5\) (or equivalent) A1
\(p = – 2\) AG
(ii) \(p = – 2\) and \(z = – 1 \Rightarrow \frac{{x – 2}}{{ – 2}} = \frac{{y – q}}{2} = – 2\) (A1)
\(x = 6\) and \(y = q – 4\) (A1)
this satisfies \(\Pi \) so \(6 + q – 4 – 3 = 9\) M1
\(q = 10\) A1
[11 marks]
Examiners report
Parts (a) and (b) were often well done, though a small number of candidates were clearly puzzled when trying to demonstrate \(\left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 3 \end{array}} \right) \ne k\left( {\begin{array}{*{20}{c}} p \\ 2 \\ 1 \end{array}} \right)\), with some scripts seen involving needlessly convoluted arguments.
Parts (a) and (b) were often well done, though a small number of candidates were clearly puzzled when trying to demonstrate \(\left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 3 \end{array}} \right) \ne k\left( {\begin{array}{*{20}{c}} p \\ 2 \\ 1 \end{array}} \right)\), with some scripts seen involving needlessly convoluted arguments.
Part (c) often proved problematic, as some candidates unsurprisingly used the sine (or cosine) of an incorrect angle, and few consequent marks were then available. Some good clear solutions were seen, occasionally complete with diagrams in the cases of the thoughtful candidates who were able to ‘work through’ the question rather than just apply a standard vector result.
Question
Find the coordinates of the point of intersection of the planes defined by the equations \(x + y + z = 3,{\text{ }}x – y + z = 5\) and \(x + y + 2z = 6\).
▶️Answer/Explanation
Markscheme
METHOD 1
for eliminating one variable from two equations (M1)
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ {2x + 2z = 8} \\ {2x + 3z = 11} \end{array}} \right.\) A1A1
for finding correctly one coordinate
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ {(2x + 2z = 8)} \\ {z = 3} \end{array}} \right.\) A1
for finding correctly the other two coordinates A1
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 1} \\ {y = – 1} \\ {z = 3} \end{array}} \right.\)
the intersection point has coordinates \((1,{\text{ }} – 1,{\text{ }}3)\)
METHOD 2
for eliminating two variables from two equations or using row reduction (M1)
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ { – 2 = 2} \\ {z = 3} \end{array}} \right.\) or \(\left( {\begin{array}{*{20}{c}} 1&1&1 \\ 0&{ – 2}&0 \\ 0&0&1 \end{array}\left| {\begin{array}{*{20}{c}} 3 \\ 2 \\ 3 \end{array}} \right.} \right)\) A1A1
for finding correctly the other coordinates A1A1
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 1} \\ {y = – 1} \\ {(z = 3)} \end{array}} \right.\) or \(\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}\left| {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ 3 \end{array}} \right.} \right)\)
the intersection point has coordinates \((1,{\text{ }} – 1,{\text{ }}3)\)
METHOD 3
\(\left| {\begin{array}{*{20}{c}} 1&1&1 \\ 1&{ – 1}&1 \\ 1&1&2 \end{array}} \right| = – 2\) (A1)
attempt to use Cramer’s rule M1
\(x = \frac{{\left| {\begin{array}{*{20}{c}} 3&1&1 \\ 5&{ – 1}&1 \\ 6&1&2 \end{array}} \right|}}{{ – 2}} = \frac{{ – 2}}{{ – 2}} = 1\) A1
\(y = \frac{{\left| {\begin{array}{*{20}{c}} 1&3&1 \\ 1&5&1 \\ 1&6&2 \end{array}} \right|}}{{ – 2}} = \frac{2}{{ – 2}} = – 1\) A1
\(z = \frac{{\left| {\begin{array}{*{20}{c}} 1&1&3 \\ 1&{ – 1}&5 \\ 1&1&6 \end{array}} \right|}}{{ – 2}} = \frac{{ – 6}}{{ – 2}} = 3\) A1
Note: Award M1 only if candidate attempts to determine at least one of the variables using this method.
[5 marks]
Examiners report
Question
Consider the lines \({l_1}\) and \({l_2}\) defined by
\({l_1}:\) r \( = \left( {\begin{array}{*{20}{c}} { – 3} \\ { – 2} \\ a \end{array}} \right) + \beta \left( {\begin{array}{*{20}{c}} 1 \\ 4 \\ 2 \end{array}} \right)\) and \({l_2}:\frac{{6 – x}}{3} = \frac{{y – 2}}{4} = 1 – z\) where \(a\) is a constant.
Given that the lines \({l_1}\) and \({l_2}\) intersect at a point P,
a.find the value of \(a\);[4]
b.determine the coordinates of the point of intersection P.[2]
▶️Answer/Explanation
Markscheme
METHOD 1
\({l_1}:\)r \( = \left( {\begin{array}{*{20}{c}} { – 3} \\ { – 2} \\ a \end{array}} \right) = \beta \left( {\begin{array}{*{20}{c}} 1 \\ 4 \\ 2 \end{array}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = – 3 + \beta } \\ {y = – 2 + 4\beta } \\ {z = a + 2\beta } \end{array}} \right.\) M1
\(\frac{{6 – ( – 3 + \beta )}}{3} = \frac{{( – 2 + 4\beta ) – 2}}{4} \Rightarrow 4 = \frac{{4\beta }}{3} \Rightarrow \beta = 3\) M1A1
\(\frac{{6 – ( – 3 + \beta )}}{3} = 1 – (a + 2\beta ) \Rightarrow 2 = – 5 – a \Rightarrow a = – 7\) A1
METHOD 2
\(\left\{ {\begin{array}{*{20}{l}} { – 3 + \beta = 6 – 3\lambda } \\ { – 2 + 4\beta = 4\lambda + 2} \\ {a + 2\beta = 1 – \lambda } \end{array}} \right.\) M1
attempt to solve M1
\(\lambda = 2,{\text{ }}\beta = 3\) A1
\(a = 1 – \lambda – 2\beta = – 7\) A1
[4 marks]
\(\overrightarrow {{\text{OP}}} = \left( {\begin{array}{*{20}{c}} { – 3} \\ { – 2} \\ { – 7} \end{array}} \right) + 3 \bullet \left( {\begin{array}{*{20}{c}} 1 \\ 4 \\ 2 \end{array}} \right)\) (M1)
\( = \left( {\begin{array}{*{20}{c}} 0 \\ {10} \\ { – 1} \end{array}} \right)\) A1
\(\therefore {\text{P}}(0,{\text{ 10, }} – 1)\)
[2 marks]
Question
The points A and B are given by \({\text{A}}(0,{\text{ }}3,{\text{ }} – 6)\) and \({\text{B}}(6,{\text{ }} – 5,{\text{ }}11)\).
The plane Π is defined by the equation \(4x – 3y + 2z = 20\).
a.Find a vector equation of the line L passing through the points A and B.[3]
b.Find the coordinates of the point of intersection of the line L with the plane Π.[3]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{AB}}} = \left( {\begin{array}{*{20}{c}} 6 \\ { – 8} \\ {17} \end{array}} \right)\) (A1)
r = \(\left( {\begin{array}{*{20}{c}} 0 \\ 3 \\ { – 6} \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} 6 \\ { – 8} \\ {17} \end{array}} \right)\) or r = \(\left( {\begin{array}{*{20}{c}} 6 \\ { – 5} \\ {11} \end{array}} \right) + \lambda \left( {\begin{array}{*{20}{c}} 6 \\ { – 8} \\ {17} \end{array}} \right)\) M1A1
Note: Award M1A0 if r = is not seen (or equivalent).
[3 marks]
substitute line L in \(\Pi :4(6\lambda ) – 3(3 – 8\lambda ) + 2( – 6 + 17\lambda ) = 20\) M1
\(82\lambda = 41\)
\(\lambda = \frac{1}{2}\) (A1)
r = \(\left( {\begin{array}{*{20}{c}} 0 \\ 3 \\ { – 6} \end{array}} \right) + \frac{1}{2}\left( {\begin{array}{*{20}{c}} 6 \\ { – 8} \\ {17} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 3 \\ { – 1} \\ {\frac{5}{2}} \end{array}} \right)\)
so coordinate is \(\left( {3,{\text{ }} – 1,{\text{ }}\frac{5}{2}} \right)\) A1
Note: Accept coordinate expressed as position vector \(\left( {\begin{array}{*{20}{c}} 3 \\ { – 1} \\ {\frac{5}{2}} \end{array}} \right)\).
[3 marks]
Question
The following figure shows a square based pyramid with vertices at O(0, 0, 0), A(1, 0, 0), B(1, 1, 0), C(0, 1, 0) and D(0, 0, 1).
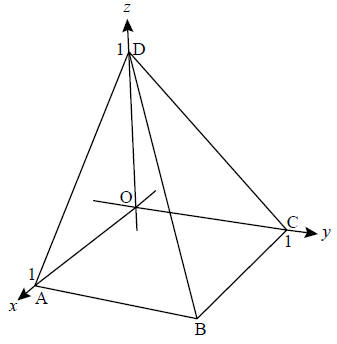
The Cartesian equation of the plane \({\Pi _2}\), passing through the points B , C and D , is \(y + z = 1\).
The plane \({\Pi _3}\) passes through O and is normal to the line BD.
\({\Pi _3}\) cuts AD and BD at the points P and Q respectively.
a.Find the Cartesian equation of the plane \({\Pi _1}\), passing through the points A , B and D.[3]
b.Find the angle between the faces ABD and BCD.[4]
c.Find the Cartesian equation of \({\Pi _3}\).[3]
d.Show that P is the midpoint of AD.[4]
e.Find the area of the triangle OPQ.[5]
▶️Answer/Explanation
Markscheme
recognising normal to plane or attempting to find cross product of two vectors lying in the plane (M1)
for example, \(\mathop {{\text{AB}}}\limits^ \to \,\, \times \mathop {{\text{AD}}}\limits^ \to = \left( \begin{gathered}
0 \hfill \\
1 \hfill \\
0 \hfill \\
\end{gathered} \right) \times \left( \begin{gathered}
– 1 \hfill \\
\,0 \hfill \\
\,1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
1 \hfill \\
0 \hfill \\
1 \hfill \\
\end{gathered} \right)\) (A1)
\({\Pi _1}\,{\text{:}}\,\,x + z = 1\) A1
[3 marks]
EITHER
\(\left( \begin{gathered}
1 \hfill \\
0 \hfill \\
1 \hfill \\
\end{gathered} \right) \bullet \left( \begin{gathered}
0 \hfill \\
1 \hfill \\
1 \hfill \\
\end{gathered} \right) = 1 = \sqrt 2 \sqrt 2 \,{\text{cos}}\,\theta \) M1A1
OR
\(\left| {\left( \begin{gathered}
1 \hfill \\
0 \hfill \\
1 \hfill \\
\end{gathered} \right) \times \left( \begin{gathered}
0 \hfill \\
1 \hfill \\
1 \hfill \\
\end{gathered} \right)} \right| = \sqrt 3 = \sqrt 2 \sqrt 2 \,{\text{sin}}\,\theta \) M1A1
Note: M1 is for an attempt to find the scalar or vector product of the two normal vectors.
\( \Rightarrow \theta = 60^\circ \left( { = \frac{\pi }{3}} \right)\) A1
angle between faces is \(20^\circ \left( { = \frac{{2\pi }}{3}} \right)\) A1
[4 marks]
\(\mathop {{\text{DB}}}\limits^ \to = \left( \begin{gathered}
\,1 \hfill \\
\,1 \hfill \\
– 1 \hfill \\
\end{gathered} \right)\) or \(\mathop {{\text{BD}}}\limits^ \to = \left( \begin{gathered}
– 1 \hfill \\
– 1 \hfill \\
\,1 \hfill \\
\end{gathered} \right)\) (A1)
\({\Pi _3}\,{\text{:}}\,\,x + y – z = k\) (M1)
\({\Pi _3}\,{\text{:}}\,\,x + y – z = 0\) A1
[3 marks]
METHOD 1
line AD : (r =)\(\left( \begin{gathered}
0 \hfill \\
0 \hfill \\
1 \hfill \\
\end{gathered} \right) + \lambda \left( \begin{gathered}
\,1 \hfill \\
\,0 \hfill \\
– 1 \hfill \\
\end{gathered} \right)\) M1A1
intersects \({\Pi _3}\) when \(\lambda – \left( {1 – \lambda } \right) = 0\) M1
so \(\lambda = \frac{1}{2}\) A1
hence P is the midpoint of AD AG
METHOD 2
midpoint of AD is (0.5, 0, 0.5) (M1)A1
substitute into \(x + y – z = 0\) M1
0.5 + 0.5 − 0.5 = 0 A1
hence P is the midpoint of AD AG
[4 marks]
METHOD 1
\({\text{OP}} = \frac{1}{{\sqrt 2 }},\,\,{\text{O}}\mathop {\text{P}}\limits^ \wedge {\text{Q}} = 90^\circ ,\,\,{\text{O}}\mathop {\text{Q}}\limits^ \wedge {\text{P}} = 60^\circ \) A1A1A1
\({\text{PQ}} = \frac{1}{{\sqrt 6 }}\) A1
area \( = \frac{1}{{2\sqrt {12} }} = \frac{1}{{4\sqrt 3 }} = \frac{{\sqrt 3 }}{{12}}\) A1
METHOD 2
line BD : (r =)\(\left( \begin{gathered}
1 \hfill \\
1 \hfill \\
0 \hfill \\
\end{gathered} \right) + \lambda \left( \begin{gathered}
– 1 \hfill \\
– 1 \hfill \\
\,1 \hfill \\
\end{gathered} \right)\)
\( \Rightarrow \lambda = \frac{2}{3}\) (A1)
\(\mathop {{\text{OQ}}}\limits^ \to = \left( \begin{gathered}
\frac{1}{3} \hfill \\
\frac{1}{3} \hfill \\
\frac{2}{3} \hfill \\
\end{gathered} \right)\) A1
area = \(\frac{1}{2}\left| {\mathop {{\text{OP}}}\limits^ \to \, \times \mathop {{\text{OQ}}}\limits^ \to } \right|\) M1
\(\mathop {{\text{OP}}}\limits^ \to = \left( \begin{gathered}
\frac{1}{2} \hfill \\
0 \hfill \\
\frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
Note: This A1 is dependent on M1.
area = \(\frac{{\sqrt 3 }}{{12}}\) A1
[5 marks
Question
The points A, B, C and D have position vectors a, b, c and d, relative to the origin O.
It is given that \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \).
The position vectors \(\mathop {{\text{OA}}}\limits^ \to \), \(\mathop {{\text{OB}}}\limits^ \to \), \(\mathop {{\text{OC}}}\limits^ \to \) and \(\mathop {{\text{OD}}}\limits^ \to \) are given by
a = i + 2j − 3k
b = 3i − j + pk
c = qi + j + 2k
d = −i + rj − 2k
where p , q and r are constants.
The point where the diagonals of ABCD intersect is denoted by M.
The plane \(\Pi \) cuts the x, y and z axes at X , Y and Z respectively.
a.i.Explain why ABCD is a parallelogram.[1]
a.ii.Using vector algebra, show that \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \).[3]
b.Show that p = 1, q = 1 and r = 4.[5]
c.Find the area of the parallelogram ABCD.[4]
d.Find the vector equation of the straight line passing through M and normal to the plane \(\Pi \) containing ABCD.[4]
e.Find the Cartesian equation of \(\Pi \).[3]
f.i.Find the coordinates of X, Y and Z.[2]
f.ii.Find YZ.[2]
▶️Answer/Explanation
Markscheme
a pair of opposite sides have equal length and are parallel R1
hence ABCD is a parallelogram AG
[1 mark]
attempt to rewrite the given information in vector form M1
b − a = c − d A1
rearranging d − a = c − b M1
hence \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) AG
Note: Candidates may correctly answer part i) by answering part ii) correctly and then deducing there
are two pairs of parallel sides.
[3 marks]
EITHER
use of \(\mathop {{\text{AB}}}\limits^ \to = \mathop {{\text{DC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
2 \hfill \\
– 3 \hfill \\
p + 3 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q + 1 \hfill \\
1 – r \hfill \\
4 \hfill \\
\end{gathered} \right)\) A1A1
OR
use of \(\mathop {{\text{AD}}}\limits^ \to = \mathop {{\text{BC}}}\limits^ \to \) (M1)
\(\left( \begin{gathered}
– 2 \hfill \\
r – 2 \hfill \\
1 \hfill \\
\end{gathered} \right) = \left( \begin{gathered}
q – 3 \hfill \\
2 \hfill \\
2 – p \hfill \\
\end{gathered} \right)\) A1A1
THEN
attempt to compare coefficients of i, j, and k in their equation or statement to that effect M1
clear demonstration that the given values satisfy their equation A1
p = 1, q = 1, r = 4 AG
[5 marks]
attempt at computing \(\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to \) (or equivalent) M1
\(\left( \begin{gathered}
– 11 \hfill \\
– 10 \hfill \\
– 2 \hfill \\
\end{gathered} \right)\) A1
area \( = \left| {\mathop {{\text{AB}}}\limits^ \to \, \times \mathop {{\text{AD}}}\limits^ \to } \right|\left( { = \sqrt {225} } \right)\) (M1)
= 15 A1
[4 marks]
valid attempt to find \(\mathop {{\text{OM}}}\limits^ \to = \left( {\frac{1}{2}\left( {a + c} \right)} \right)\) (M1)
\(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right)\) A1
the equation is
r = \(\left( \begin{gathered}
1 \hfill \\
\frac{3}{2} \hfill \\
– \frac{1}{2} \hfill \\
\end{gathered} \right) + t\left( \begin{gathered}
11 \hfill \\
10 \hfill \\
2 \hfill \\
\end{gathered} \right)\) or equivalent M1A1
Note: Award maximum M1A0 if ‘r = …’ (or equivalent) is not seen.
[4 marks]
attempt to obtain the equation of the plane in the form ax + by + cz = d M1
11x + 10y + 2z = 25 A1A1
Note: A1 for right hand side, A1 for left hand side.
[3 marks]
putting two coordinates equal to zero (M1)
\({\text{X}}\left( {\frac{{25}}{{11}},\,0,\,0} \right),\,\,{\text{Y}}\left( {0,\,\frac{5}{2},\,0} \right),\,\,{\text{Z}}\left( {0,\,0,\,\frac{{25}}{2}} \right)\) A1
[2 marks]
\({\text{YZ}} = \sqrt {{{\left( {\frac{5}{2}} \right)}^2} + {{\left( {\frac{{25}}{2}} \right)}^2}} \) M1
\( = \sqrt {\frac{{325}}{2}} \left( { = \frac{{5\sqrt {104} }}{4} = \frac{{5\sqrt {26} }}{2}} \right)\) A1
[4 marks]
Question
Find a vector that is normal to the plane containing the lines \(L_1\) , and \(L_2\) , whose equations are:
\(L_1 : r = i + k + \lambda (2i + j – 2k)\) \(L_2: r = 3i + 2j + 2k + \mu (j + 3k)\)
▶️Answer/Explanation
Ans:
A vector that is normal to the plane is given by the vector product \(d1 × d2\) where \(d1\) and \(d2\) are the direction vectors of the lines \(L_1\) and \(L_2\) respectively.
\(d1 × d2 = \begin{vmatrix} i& j& k\\ 2 & 1 & -2\\ 0 & 1 & 3 \end{vmatrix}\)
\(= 5i – 6j + 2k\) (or any multiple)