Question: [Maximum mark: 4]
The number of hours spent exercising each week by a group of students is shown in the following table.
| Exercising time (in hours) | Number of students |
| 2 | 5 |
| 3 | 1 |
| 4 | 4 |
| 5 | 3 |
| 6 | x |
The median is 4.5 hours.
(a) Find the value of x .
(b) Find the standard deviation.
▶️Answer/Explanation
Ans:
(a) EITHER
recognising that half the total frequency is 10 (may be seen in an ordered list or indicated on the frequency table)
OR
5 + 1 + 4 = 3 + x
OR
\(\sum f = 20\)
THEN
x = 7
(b) METHOD 1
1.58429…
1.58
METHOD 2
EITHER
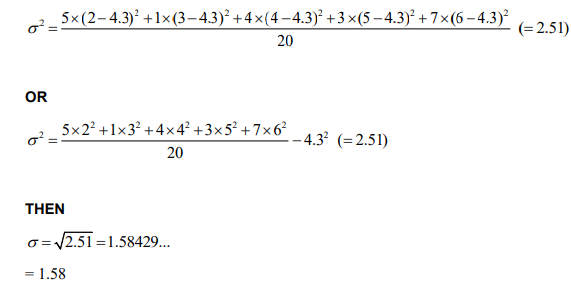
Question
Consider the data set \(\{ k – 2,{\text{ }}k,{\text{ }}k + 1,{\text{ }}k + 4\} {\text{ , where }}k \in \mathbb{R}\) .
(a) Find the mean of this data set in terms of k.
Each number in the above data set is now decreased by 3.
(b) Find the mean of this new data set in terms of k.
▶️Answer/Explanation
Markscheme
(a) Use of \(\bar x = \frac{{\sum\limits_{i = 1}^4 {{x_i}} }}{n}\) (M1)
\(\bar x = \frac{{(k – 2) + k + (k + 1) + (k + 4)}}{4}\) (A1)
\(\bar x = \frac{{4k + 3}}{4}\,\,\,\,\,\left( { = k + \frac{3}{4}} \right)\) A1 N3
(b) Either attempting to find the new mean or subtracting 3 from their \({\bar x}\) (M1)
\(\bar x = \frac{{4k + 3}}{4} – 3\,\,\,\,\,\left( { = \frac{{4k – 9}}{4},{\text{ }}k – \frac{9}{4}} \right)\) A1 N2
[5 marks]
Examiners report
This was an easy question that was well done by most candidates. Careless arithmetic errors caused some candidates not to earn full marks. Only a few candidates realised that part (b) could be answered correctly by directly subtracting 3 from their answer to part (a). Most successful responses were obtained by redoing the calculation from part (a).
Question
Consider the data set \(\{ 2,{\text{ }}x,{\text{ }}y,{\text{ }}10,{\text{ }}17\} ,{\text{ }}x,{\text{ }}y \in {\mathbb{Z}^ + }\) and \(x < y\).
The mean of the data set is \(8\) and its variance is \(27.6\).
Find the value of \(x\) and the value of \(y\).
▶️Answer/Explanation
Markscheme
use of \(\mu = \frac{{\sum\limits_{i = 1}^k {{f_i}{x_i}} }}{n}{\text{ }}\) to obtain \(\frac{{2 + x + y + 10 + 17}}{5} = 8\) (M1)
\(x + y = 11\) A1
EITHER
use of \({\sigma ^2} = \frac{{\sum\limits_{i = 1}^k {{f_i}{{({x_i} – \mu )}^2}} }}{n}\) to obtain \(\frac{{{{( – 6)}^2} + {{(x – 8)}^2} + {{(y – 8)}^2} + {2^2} + {9^2}}}{5} = 27.6\) (M1)
\({(x – 8)^2} + {(y – 8)^2} = 17\) A1
OR
use of \({\sigma ^2} = \frac{{\sum\limits_{i = 1}^k {{f_i}x_i^2} }}{n} – {\mu ^2}\) to obtain \(\frac{{{2^2} + {x^2} + {y^2} + {{10}^2} + {{17}^2}}}{5} – {8^2} = 27.6\) (M1)
\({x^2} + {y^2} = 65\) A1
THEN
attempting to solve the two equations (M1)
\(x = 4\;\;\;\)and\(\;\;\;y = 7\;\;\;({\text{only as }}x < y)\)A1 N4
Note: Award A0 for \(x = 7\) and \(y = 4\).
Note: Award (M1)A1(M0)A0(M1)A1 for \(x + y = 11 \Rightarrow x = 4\) and \(y = 7\).
[6 marks]
Examiners report
Reasonably well done. Most candidates were able to obtain \(x + y = 11\). Most manipulation errors occurred when candidates attempted to form the variance equation in terms of \(x\) and \(y\). Some candidates did not apply the condition \(x < y\) when determining their final answer.
Question
The data of the goals scored by players in a football club during a season are given in the following table.
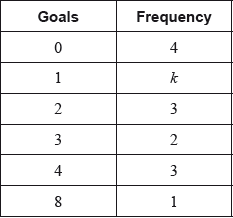
a.Given that the mean number of goals scored per player is \(1.95\) , find the value of \(k\).[3]
(i) Find the correct mean number of goals scored per player.
(ii) Find the correct standard deviation of the number of goals scored per player.[3]
▶️Answer/Explanation
Markscheme
\(\frac{{0 \bullet 4 + 1 \bullet k + 2 \bullet 3 + 3 \bullet 2 + 4 \bullet 3 + 8 \bullet 1}}{{13 + k}} = 1.95\;\;\;\left( {\frac{{k + 32}}{{k + 13}} = 1.95} \right)\) (M1)
attempting to solve for \(k\) (M1)
\(k = 7\) A1
[3 marks]
(i) \(\frac{{7 + 32 + 22}}{{7 + 13 + 1}} = 2.90\;\;\;\left( { = \frac{{61}}{{21}}} \right)\) (M1)A1
(ii) standard deviation \( = 4.66\) A1
Note: Award A0 for \(4.77\).
[3 marks]
Total [6 marks]
Examiners report
[N/A]
[N/A]
Question
Six balls numbered 1, 2, 2, 3, 3, 3 are placed in a bag. Balls are taken one at a time from the bag at random and the number noted. Throughout the question a ball is always replaced before the next ball is taken.
Three balls are taken from the bag. Find the probability that
A single ball is taken from the bag. Let \(X\) denote the value shown on the ball.
a.Find \({\text{E}}(X)\).[2]
b.i.the total of the three numbers is 5;[3]
b.ii.the median of the three numbers is 1.[3]
c.Ten balls are taken from the bag. Find the probability that less than four of the balls are numbered 2.[3]
d.Find the least number of balls that must be taken from the bag for the probability of taking out at least one ball numbered 2 to be greater than 0.95.[3]
e.Another bag also contains balls numbered 1 , 2 or 3.
Eight balls are to be taken from this bag at random. It is calculated that the expected number of balls numbered 1 is 4.8 , and the variance of the number of balls numbered 2 is 1.5.
Find the least possible number of balls numbered 3 in this bag.[8]
▶️Answer/Explanation
Markscheme
\({\text{E}}(X) = 1 \times \frac{1}{6} + 2 \times \frac{2}{6} + 3 \times \frac{3}{6} = \frac{{14}}{6}{\text{ }}\left( { = \frac{7}{3} = 2.33} \right)\) (M1)A1
[2 marks]
\(3 \times {\text{P}}(113) + 3 \times {\text{P}}(122)\) (M1)
\(3 \times \frac{1}{6} \times \frac{1}{6} \times \frac{1}{2} + 3 \times \frac{1}{6} \times \frac{1}{3} \times \frac{1}{3} = \frac{7}{{72}}{\text{ }}( = 0.0972)\) A1
Note: Award M1 for attempt to find at least four of the cases.
[3 marks]
recognising 111 as a possibility \(\left( {{\text{implied by }}\frac{1}{{216}}} \right)\) (M1)
recognising 112 and 113 as possibilities \(\left( {{\text{implied by }}\frac{2}{{216}}{\text{ and }}\frac{3}{{216}}} \right)\) (M1)
seeing the three arrangements of 112 and 113 (M1)
\({\text{P}}(111) + 3 \times {\text{P}}(112) + 3 \times {\text{P}}(113)\)
\( = \frac{1}{{216}} + \frac{6}{{216}} + \frac{9}{{216}} = \frac{{16}}{{216}}{\text{ }}\left( { = \frac{2}{{27}} = 0.0741} \right)\) A1
[3 marks]
let the number of twos be \(X,{\text{ }}X \sim B\left( {10,{\text{ }}\frac{1}{3}} \right)\) (M1)
\({\text{P}}(X < 4) = {\text{P}}(X \leqslant 3) = 0.559\) (M1)A1
[3 marks]
let \(n\) be the number of balls drawn
\({\text{P}}(X \geqslant 1) = 1 – {\text{P}}(X = 0)\) M1
\( = 1 – {\left( {\frac{2}{3}} \right)^n} > 0.95\) M1
\({\left( {\frac{2}{3}} \right)^n} > 0.05\)
\(n = 8\) A1
[3 marks]
\(8{p_1} = 4.8 \Rightarrow {p_1} = \frac{3}{5}\) (M1)A1
\(8{p_2}(1 – {p_2}) = 1.5\) (M1)
\(p_2^2 – {p_2} – 0.1875 = 0\) (M1)
\({p_2} = \frac{1}{4}{\text{ }}\left( {{\text{or }}\frac{3}{4}} \right)\) A1
reject \(\frac{3}{4}\) as it gives a total greater than one
\({\text{P}}(1{\text{ or }}2) = \frac{{17}}{{20}}{\text{ or P}}(3) = \frac{3}{{20}}\) (A1)
recognising LCM as 20 so min total number is 20 (M1)
the least possible number of 3’s is 3 A1
[8 marks]
Question
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let \({\text{P}}(X = n)\) be the probability that Kati obtains her third voucher on the \(n{\text{th}}\) bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that \({\text{P}}(X = n) = \frac{{{n^2} + an + b}}{{2000}} \times {0.9^{n – 3}}\) for \(n \geqslant 3,{\text{ }}n \in \mathbb{N}\).
Kati’s mother goes to the shop and buys \(x\) chocolate bars. She takes the bars home for Kati to open.
a.Show that \({\text{P}}(X = 3) = 0.001\) and \({\text{P}}(X = 4) = 0.0027\).[3]
b.Find the values of the constants \(a\) and \(b\).[5]
c.Deduce that \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{0.9(n – 1)}}{{n – 3}}\) for \(n > 3\).[4]
d.(i) Hence show that \(X\) has two modes \({m_1}\) and \({m_2}\).
(ii) State the values of \({m_1}\) and \({m_2}\).[5]
e.Determine the minimum value of \(x\) such that the probability Kati receives at least one free gift is greater than 0.5.[3]
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 3) = {(0.1)^3}\) A1
\( = 0.001\) AG
\({\text{P}}(X = 4) = {\text{P}}(VV\bar VV) + {\text{P}}(V\bar VVV) + {\text{P}}(\bar VVVV)\) (M1)
\( = 3 \times {(0.1)^3} \times 0.9\) (or equivalent) A1
\( = 0.0027\) AG
[3 marks]
METHOD 1
attempting to form equations in \(a\) and \(b\) M1
\(\frac{{9 + 3a + b}}{{2000}} = \frac{1}{{1000}}{\text{ }}(3a + b = – 7)\) A1
\(\frac{{16 + 4a + b}}{{2000}} \times \frac{9}{{10}} = \frac{{27}}{{10\,000}}{\text{ }}(4a + b = – 10)\) A1
attempting to solve simultaneously (M1)
\(a = – 3,{\text{ }}b = 2\) A1
METHOD 2
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) M1
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) (M1)A1
\( = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) A1
\(a = – 3,b = 2\) A1
Note: Condone the absence of \({0.9^{n – 3}}\) in the determination of the values of \(a\) and \(b\).
[5 marks]
METHOD 1
EITHER
\({\text{P}}(X = n) = \frac{{{n^2} – 3n + 2}}{{2000}} \times {0.9^{n – 3}}\) (M1)
OR
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n – 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n – 3}}\) (M1)
THEN
\( = \frac{{(n – 1)(n – 2)}}{{2000}} \times {0.9^{n – 3}}\) A1
\({\text{P}}(X = n – 1) = \frac{{(n – 2)(n – 3)}}{{2000}} \times {0.9^{n – 4}}\) A1
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{(n – 1)(n – 2)}}{{(n – 2)(n – 3)}} \times 0.9\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
METHOD 2
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}} = \frac{{\frac{{{n^2} – 3n + 2}}{{2000}} \times {{0.9}^{n – 3}}}}{{\frac{{{{(n – 1)}^2} – 3(n – 1) + 2}}{{2000}} \times {{0.9}^{n – 4}}}}\) (M1)
\( = \frac{{0.9({n^2} – 3n + 2)}}{{({n^2} – 5n + 6)}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{0.9(n – 1)(n – 2)}}{{(n – 2)(n – 3)}}\) A1
\( = \frac{{0.9(n – 1)}}{{n – 3}}\) AG
[4 marks]
(i) attempting to solve \(\frac{{0.9(n – 1)}}{{n – 3}} = 1\) for \(n\) M1
\(n = 21\) A1
\(\frac{{0.9(n – 1)}}{{n – 3}} < 1 \Rightarrow n > 21\) R1
\(\frac{{0.9(n – 1)}}{{n – 3}} > 1 \Rightarrow n < 21\) R1
\(X\) has two modes AG
Note: Award R1R1 for a clearly labelled graphical representation of the two inequalities (using \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n – 1)}}\)).
(ii) the modes are 20 and 21 A1
[5 marks]
METHOD 1
\(Y \sim {\text{B}}(x,{\text{ }}0.1)\) (A1)
attempting to solve \({\text{P}}(Y \geqslant 3) > 0.5\) (or equivalent eg \(1 – {\text{P}}(Y \leqslant 2) > 0.5\)) for \(x\) (M1)
Note: Award (M1) for attempting to solve an equality (obtaining \(x = 26.4\)).
\(x = 27\) A1
METHOD 2
\(\sum\limits_{n = 0}^x {{\text{P}}(X = n) > 0.5} \) (A1)
attempting to solve for \(x\) (M1)
\(x = 27\) A1
[3 marks]