Question
A team of 6 players is to be selected from 10 volleyball players, of whom 8 are boys and 2 are girls.
a.In how many ways can the team be selected?[2]
b.In how many of these selections is exactly one girl in the team?[3]
c.If the selection of the team is made at random, find the probability that exactly one girl is in the team.[2]
▶️Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
{10} \\
6
\end{array}} \right) = 210\) (M1)A1
[2 marks]
\(2 \times \left( {\begin{array}{*{20}{c}}
8 \\
5
\end{array}} \right) = 112\) (M1)A1A1
Note: Accept \(210 – 28 – 70 = 112\)
[3 marks]
\(\frac{{112}}{{210}}\,\,\left( { = \frac{8}{{15}} = 0.533} \right)\) (M1)A1
[2 marks]
Question
Kathy plays a computer game in which she has to find the path through a maze within a certain time. The first time she attempts the game, the probability of success is known to be 0.75. In subsequent attempts, if Kathy is successful, the difficulty increases and the probability of success is half the probability of success on the previous attempt. However, if she is unsuccessful, the probability of success remains the same. Kathy plays the game three times consecutively.
a.Find the probability that she is successful in all three games.[2]
b.Assuming that she is successful in the first game, find the probability that she is successful in exactly two games.[6]
▶️Answer/Explanation
Markscheme
\({\text{P(WWW)}} = 0.75 \times 0.375 \times 0.1875 = 0.0527{\text{ (3sf) }}\left( {\frac{3}{4} \times \frac{3}{8} \times \frac{3}{{16}} = \frac{{27}}{{512}}} \right)\) (M1)A1
[2 marks]
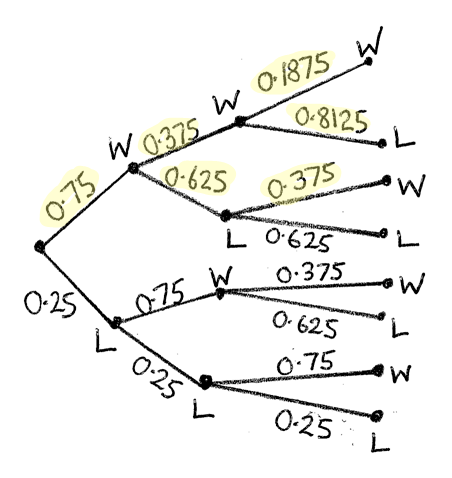(M1)(A1)
Note: Award M1 for any reasonable attempt to use a tree diagram showing that three games were played (do not award M1 for tree diagrams that only show the first two games) and A1 for the highlighted probabilities.
\(\left. {{\text{P(wins 2 games}}\,} \right|{\text{wins first game)}} = \frac{{{\text{P(WWL, WLW)}}}}{{{\text{P(wins first game)}}}}\) (M1)
\( = \frac{{0.75 \times 0.375 \times 0.8125 + 0.75 \times 0.625 \times 0.375}}{{0.75}}\) (A1)(A1)
\( = 0.539{\text{ (3sf) }}\left( {{\text{or }}\frac{{69}}{{128}}} \right)\) A1
Note: Candidates may use the tree diagram to obtain the answer without using the conditional probability formula, ie,
\(\left. {{\text{P(wins 2 games}}\,} \right|{\text{wins first game)}} = 0.375 \times 0.8125 + 0.625 \times 0.375 = 0.539.\)
[6 marks]
Question
a.Find the term in \({x^5}\) in the expansion of \((3x + A){(2x + B)^6}\).[4]
it to decide if they are going to eat a cookie.
Mina throws her die just once and she eats a cookie if she throws a four, a five or a six.
Norbert throws his die six times and each time eats a cookie if he throws a five or a six.
Calculate the probability that five cookies are eaten.[4]
▶️Answer/Explanation
Markscheme
\(\left( {A\left( \begin{array}{l}6\\5\end{array} \right){2^5}B + 3\left( \begin{array}{l}6\\4\end{array} \right){2^4}{B^2}} \right){x^5}\) M1A1A1
\( = \left( {192AB + 720{B^2}} \right){x^5}\) A1
[4 marks]
METHOD 1
\(x = \frac{1}{6},{\text{ }}A = \frac{3}{6}\left( { = \frac{1}{2}} \right),{\text{ }}B = \frac{4}{6}\left( { = \frac{2}{3}} \right)\) A1A1A1
probability is \(\frac{4}{{81}}{\text{ }}( = 0.0494)\) A1
METHOD 2
P (5 eaten) =P (M eats 1) P (N eats 4) + P (M eats 0) P (N eats 5) (M1)
\( = \frac{1}{2}\left( \begin{array}{l}6\\4\end{array} \right){\left( {\frac{1}{3}} \right)^4}{\left( {\frac{2}{3}} \right)^2} + \frac{1}{2}\left( \begin{array}{l}6\\5\end{array} \right){\left( {\frac{1}{3}} \right)^5}\left( {\frac{2}{3}} \right)\) (A1)(A1)
\( = \frac{4}{{81}}{\text{ }}( = 0.0494)\) A1
[4 marks]