Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
a.Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.[4]
b.Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .[3]
▶️Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
a.Draw a tree diagram to represent these events and their outcomes.[1]
b.What is the probability that the “Tigers” soccer team wins?[2]
c.Given that the “Tigers” soccer team won, what is the probability that it rained on that day?[2]
▶️Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”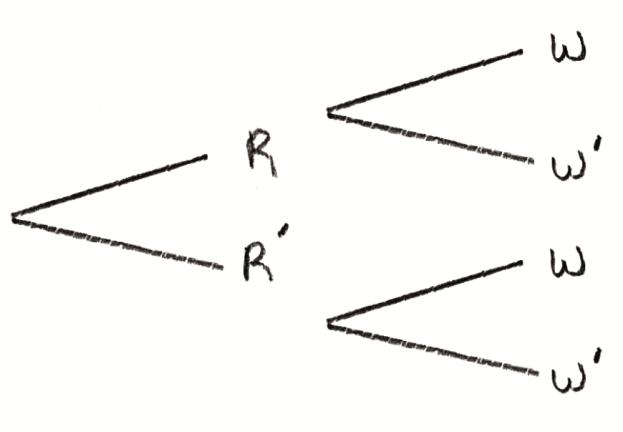 A1
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
a.Draw a tree diagram to represent these events and their outcomes.[1]
b.What is the probability that the “Tigers” soccer team wins?[2]
c.Given that the “Tigers” soccer team won, what is the probability that it rained on that day?[2]
▶️Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win” A1
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Question
Consider the following functions:
\[f(x) = \frac{{2{x^2} + 3}}{{75}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{{\left| {3x – 4} \right|}}{{10}},{\text{ }}x \in \mathbb{R}{\text{ }}.\]
aState the range of f and of g .[2]
b.Find an expression for the composite function \(f \circ g(x)\) in the form \(\frac{{a{x^2} + bx + c}}{{3750}}\), where \(a,{\text{ }}b{\text{ and }}c \in \mathbb{Z}\) .[4]
c.(i) Find an expression for the inverse function \({f^{ – 1}}(x)\) .
(ii) State the domain and range of \({f^{ – 1}}\) .[4]
d.The domains of f and g are now restricted to {0, 1, 2, 3, 4} .
By considering the values of f and g on this new domain, determine which of f and g could be used to find a probability distribution for a discrete random variable X , stating your reasons clearly.[6]
e.Using this probability distribution, calculate the mean of X .[2]
▶️Answer/Explanation
Markscheme
\(f(x) \geqslant \frac{1}{{25}}\) A1
\(g(x) \in \mathbb{R},{\text{ }}g(x) \geqslant 0\) A1
[2 marks]
\(f \circ g(x) = \frac{{2{{\left( {\frac{{3x – 4}}{{10}}} \right)}^2} + 3}}{{75}}\) M1A1
\( = \frac{{\frac{{2(9{x^2} – 24x + 16)}}{{100}} + 3}}{{75}}\) (A1)
\( = \frac{{9{x^2} – 24x + 166}}{{3750}}\) A1
[4 marks]
(i) METHOD 1
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\({x^2} = \frac{{75y – 3}}{2}\) M1
\(x = \sqrt {\frac{{75y – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
METHOD 2
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\(x = \frac{{2{y^2} + 3}}{{75}}\) M1
\(y = \sqrt {\frac{{75x – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
(ii) domain: \(x \geqslant \frac{1}{{25}}\) ; range: \({f^{ – 1}}(x) \geqslant 0\) A1
[4 marks]
probabilities from \(f(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
probabilities from \(g(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
only in the case of \(f(x)\) does \(\sum {P(X = x) = 1} \) , hence only \(f(x)\) can be used as a probability mass function A2
[6 marks]
\(E(x) = \sum {x \cdot {\text{P}}(X = x)} \) M1
\( = \frac{5}{{75}} + \frac{{22}}{{75}} + \frac{{63}}{{75}} + \frac{{140}}{{75}} = \frac{{230}}{{75}}\left( { = \frac{{46}}{{15}}} \right)\) A1
[2 marks]
Examiners report
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
Question
Two events A and B are such that \({\text{P}}(A \cup B) = 0.7\) and \({\text{P}}(A|B’) = 0.6\).
Find \({\text{P}}(B)\).
▶️Answer/Explanation
Markscheme
Note: Be aware that an unjustified assumption of independence will also lead to P(B) = 0.25, but is an invalid method.
METHOD 1
\({\text{P}}(A’|B’) = 1 – {\text{P}}(A|B’) = 1 – 0.6 = 0.4\) M1A1
\({\text{P}}(A’|B’) = \frac{{{\text{P}}(A’ \cap B’)}}{{{\text{P}}(B’)}}\)
\({\text{P}}(A’ \cap B’) = {\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
\(0.4 = \frac{{0.3}}{{{\text{P}}(B’)}} \Rightarrow {\text{P(}}B’) = 0.75\) (M1)A1
\({\text{P}}(B) = 0.25\) A1
(this method can be illustrated using a tree diagram)
[6 marks]
METHOD 2
\({\text{P}}\left( {(A \cup B)’} \right) = 1 – 0.7 = 0.3\) A1
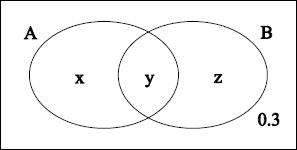
\({\text{P}}(A|B’) = \frac{x}{{x + 0.3}} = 0.6\) M1A1
\(x = 0.6x + 0.18\)
\(0.4x = 0.18\)
\(x = 0.45\) A1
\({\text{P}}(A \cup B) = x + y + z\)
\({\text{P}}(B) = y + z = 0.7 – 0.45\) (M1)
\( = 0.25\) A1
[6 marks]
METHOD 3
\(\frac{{{\text{P}}(A \cap B’)}}{{{\text{P}}(B’)}} = 0.6{\text{ (or P}}(A \cap B’) = 0.6{\text{P}}(B’)\) M1
\({\text{P}}(A \cap B’) = {\text{P}}(A \cup B) – {\text{P}}(B)\) M1A1
\({\text{P}}(B’) = 1 – {\text{P}}(B)\)
\(0.7 – {\text{P}}(B) = 0.6 – 0.6{\text{P}}(B)\) M1(A1)
\(0.1 = 0.4{\text{P}}(B)\)
\({\text{P}}(B) = \frac{1}{4}\) A1
[6 marks]
Examiners report
There is a great variety of ways to approach this question and there were plenty of very good solutions produced, all of which required an insight into the structure of conditional probability. A few candidates unfortunately assumed independence and so did not score well.