Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
b.Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.[4]
b.Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .[3]
▶️Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
a.Draw a tree diagram to represent these events and their outcomes.[1]
b.What is the probability that the “Tigers” soccer team wins?[2]
c.Given that the “Tigers” soccer team won, what is the probability that it rained on that day?[2]
▶️Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”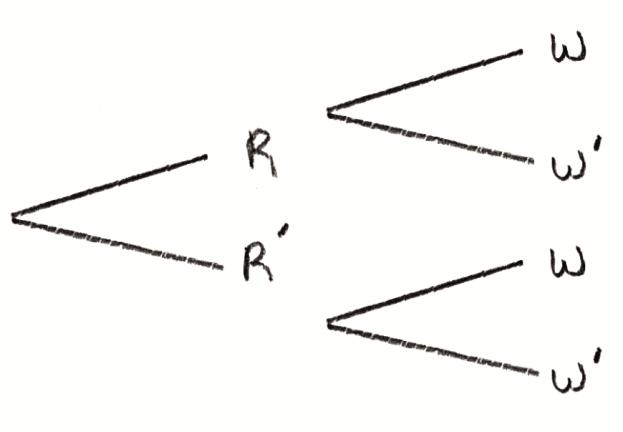 A1
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
Consider the following functions:
\[f(x) = \frac{{2{x^2} + 3}}{{75}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{{\left| {3x – 4} \right|}}{{10}},{\text{ }}x \in \mathbb{R}{\text{ }}.\]
a.State the range of f and of g .[2]
b.Find an expression for the composite function \(f \circ g(x)\) in the form \(\frac{{a{x^2} + bx + c}}{{3750}}\), where \(a,{\text{ }}b{\text{ and }}c \in \mathbb{Z}\) .[4]
d.(i) Find an expression for the inverse function \({f^{ – 1}}(x)\) .
(ii) State the domain and range of \({f^{ – 1}}\) .[4]
d.The domains of f and g are now restricted to {0, 1, 2, 3, 4} .
By considering the values of f and g on this new domain, determine which of f and g could be used to find a probability distribution for a discrete random variable X , stating your reasons clearly.[6]
e.Using this probability distribution, calculate the mean of X .[2]
▶️Answer/Explanation
Markscheme
\(f(x) \geqslant \frac{1}{{25}}\) A1
\(g(x) \in \mathbb{R},{\text{ }}g(x) \geqslant 0\) A1
[2 marks]
\(f \circ g(x) = \frac{{2{{\left( {\frac{{3x – 4}}{{10}}} \right)}^2} + 3}}{{75}}\) M1A1
\( = \frac{{\frac{{2(9{x^2} – 24x + 16)}}{{100}} + 3}}{{75}}\) (A1)
\( = \frac{{9{x^2} – 24x + 166}}{{3750}}\) A1
[4 marks]
(i) METHOD 1
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\({x^2} = \frac{{75y – 3}}{2}\) M1
\(x = \sqrt {\frac{{75y – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
METHOD 2
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\(x = \frac{{2{y^2} + 3}}{{75}}\) M1
\(y = \sqrt {\frac{{75x – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
(ii) domain: \(x \geqslant \frac{1}{{25}}\) ; range: \({f^{ – 1}}(x) \geqslant 0\) A1
[4 marks]
probabilities from \(f(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
probabilities from \(g(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
only in the case of \(f(x)\) does \(\sum {P(X = x) = 1} \) , hence only \(f(x)\) can be used as a probability mass function A2
[6 marks]
\(E(x) = \sum {x \cdot {\text{P}}(X = x)} \) M1
\( = \frac{5}{{75}} + \frac{{22}}{{75}} + \frac{{63}}{{75}} + \frac{{140}}{{75}} = \frac{{230}}{{75}}\left( { = \frac{{46}}{{15}}} \right)\) A1
[2 marks]
Examiners report
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
MAA HL 4.13 COUNTING AND PROBABILITY-neha
Question
There are 12 students in a class. Find the number of all possible ways
(a) to select 4 students
(b) to select 8 students
(c) to select 2 students
(d) to select 1 student
(e) to select all 12 students
(f) to split the students into two groups of equal size.
▶️Answer/Explanation
Ans
(a) and (b) \(\binom{12}{4}=\binom{12}{8}=495\) (c) \(\binom{12}{2}=66\)
(d) \(\binom{12}{1}=12\) (e) \(\binom{12}{12}=1\) (f) \(\binom{12}{6}=924\)
Question
There are 12 students in a class. Find the number of all possible ways
(a) to select 4 students to sit in a row of 4 seats.
(b) to select 8 students to sit in a row of 8 seats
(c) to arrange all 12 students in a row of 12 seats.
▶️Answer/Explanation
Ans
(a) \(12P4=11,880\) OR \(\underline{12}\times \underline{11}\times \underline{10}\times \underline{9}=11,880\)
(b) \(12P8=19,958,400\) OR \(\underline{12}\times\underline{11}\times\underline{10}\times\underline{9}\times\underline{8}\times\underline{7}\times\underline{6}\times\underline{5}=19,958,400\)
(c) \(12!=479,001,600\)
Question
There are 12 students in a class, of which 7 are girls and 5 are boys. The students must be arranged in a row of 12 seats.
(a) Find the number of possible arrangements
(i) if girls have to sit next to each other and boys have to sit next to each other.
(ii) if only girls have to sit next to each other.
(b) The students are arranged at random. Find the probability
(i) that girls sit next to each other and boys sit next to each other.
(ii) that only girls sit next to each other.
▶️Answer/Explanation
Ans
(a) (i) \(7!\times5!\times2\)
(ii) METHOD A:
Consider girls as one object 7G, arrange the 6 objects 7G B B B B B
Thus \(6!\times 7!\)
METHOD B:
12 seats _ _ _ _ _ _ _ _ _ _ _ _
The first girl must sit from seat 1 to seat 6 (6 ways)
Thus \(6\times 7!\times 5!\)
(b) The total number of arrangements is \(12!\) We divide the results in (a) by \(12!\)
(i) \(\frac{7!\times 5!\times 2}{12!}=\frac{1}{396}\) (ii) \(\frac{6!\times 7!}{12!}=\frac{1}{132}\)
Question
In a waiting room there is a number of students and some available seats in a row.
Find the number of possible arrangements
(a) if we have 12 students but only 3 seats.
(b) if we have only 3 students and 12 available seats.
▶️Answer/Explanation
Ans
(a) \(12P3=12\times 11\times 10=1320\)
(b) METHOD A
Select 3 seats: \(12C3\) and then arrange the \(3\) students: \(3!\).
Number of ways: \(12C3 × 3! = 1320\)
METHOD B
Select 3 seats out of 12 to assign them to the 3 students:
\(12P3 = 12 × 11 × 10 = 1320\)
Question
There are 12 students in a class, 10 boys and only 2 girls. The students must be arranged in a row of 12 seats.
(a) Find the number of possible arrangements
(i) if the two girls have to sit next to each other.
(ii) if the two girls have to be separated.
(b) The students are arranged at random. Find the probability
(i) that the two girls sit next to each other.
(ii) that the two girls are separated.
▶️Answer/Explanation
Ans
(a) (i) METHOD A \(2G\) as one object, \(11\) objects can be arranged in \(11!\) ways.
The two girls in \(2\) ways
Total number = \(11! × 2\)
METHOD B \(11×2\) ways to place the \(2\) girls and \(10!\) ways to arrange the boys
Total number = \(11 × 2 × 10! = 2 × 11!\)
(ii) \(12!-2\times 11!\)
(b) (i) \(\frac{2\times 11!}{12!}=\frac{1}{6}\) (ii) \(1-\frac{1}{6}=\frac{5}{6}\)
Question
There are 12 students in a class, 9 boys and only 3 girls. The students must be arranged in a row of 12 seats. Find the number of possible arrangements
(a) if the three girls have to sit next to each other.
(b) if not all the three girls sit next to each other (thus two of them may sit together)
(c) if the three girls are separated.
▶️Answer/Explanation
Ans
(a) METHOD A \(3G\) as one object, \(10\) objects can be arranged in \(10!\) ways.
The three girls in \(3!\) ways
Total number = \(10! × 3!\)
METHOD B \(10×3!\) ways to place the \(3\) girls and \(9!!\) ways to arrange the boys
Total number = \(10 × 3! × 9! = 3!×10!\)
(b) \(12!-3!\times 10!\)
(c) Think of the \(9\) boys as “barriers” that form \(10\) possible seats for the \(3\) girls
_ B _ B _ B _ B _ B _ B _ B _ B _ B _
Choose \(3\) seats out of the \(10\) and place the girls: \(10C3 × 3! = 10×9×8\)
Possible arrangements for the boys \(9!\)
Total number = \(10×9×8 × 9! = 72 × 10!\)
Question
There are 12 students in a class, 9 boys and only 3 girls. Three students are selected at random to form a committee. Find the probability
(a) that the committee contains only boys.
(b) that the committee contains only students of the same gender.
(c) that the committee contains two boys and one girl.
(d) that the committee contains more boys than girls.
▶️Answer/Explanation
Ans
(a) \(\frac{\binom{9}{3}\binom{3}{0}}{\binom{12}{3}}=\frac{\binom{9}{3}}{\binom{12}{3}}=\frac{21}{55}\)
(b) \(\frac{\binom{9}{3}\binom{3}{0}+\binom{9}{0}\binom{3}{3}}{\binom{12}{3}}=\frac{\binom{9}{3}+1}{\binom{12}{3}}=\frac{17}{44}\)
(c) \(\frac{\binom{9}{2}\binom{3}{1}}{\binom{12}{3}}=\frac{27}{55}\)
(d) \(\frac{\binom{9}{3}\binom{3}{0}+\binom{9}{2}\binom{3}{1}}{\binom{12}{3}}=\frac{48}{55}\)
Question
We construct 5-digit codes using all digits except 0 (that is the nine digits 1,2,3,4,5,6,7,8,9).
For example, 25439, 25518, 77788 are some of the possible codes. Find
(a) the total number of possible codes
(b) the number of possible codes of different digits (no digit can be repeated).
(c) the number of codes which are even (last digit is 2,4,6 or 8).
(d) the number of codes which contain only even digits .
(e) the number of codes that do not contain the digit 1.
(f) the number of codes that contain the digit 1.
(g) the probability that a code contains the digit 1.
▶️Answer/Explanation
Ans
(a) \(9^{5}=59049\) (b) \(9\times 8\times 7\times 6\times 5=15120\)
(c) \(9^{4}\times 4=26244\) (d) \(4^{5}=1024\)
(e) \(8^{5}=32768\) (f) \(9^{5}-8^{5}=26281\)
(g) \(\frac{9^{5}-8^{5}}{9^{5}}=1-\frac{8^{5}}{9^{5}}=0.445 (3sf)\)
Question
Find
(a) the total number of 5-digit numbers
(b) the number of 5-digit numbers of different digits (no digit can be repeated).
(c) the number of 5-digit numbers which contain only even digits.
(d) the number of 5-digit numbers that contain two 3s and three 2s .
(e) the number of 5-digit numbers that do not contain the digit 1.
(f) the number of 5-digit numbers that contain the digit 1.
(g) the probability that a 5-digit number contains the digit 1.
▶️Answer/Explanation
Ans
(a) \(9\times 10^{4}=90000\) OR \(99999-9999=90000\) (b) \(9\times 9\times 8\times 7\times 6=27216\)
(c) \(4\times 5^{4}=2500\) (d) \(5C2=10\)
(e) \(8\times 9^{4}=52488\) (f) \(9\times 10^{4}-8\times 9^{4}=37512\)
(g) \(\frac{9\times 10^{4}-8\times 9^{4}}{9\times 10^{4}}=\frac{37512}{90000}=0.4168\)
Question
A deck of 52 playing cards consists of
4 suits (♠,♣,♥,♦),
of 13 ranks each (A,2,3,4,5,6,7,8,9,10,J,Q,K)
We select 2 cards. Find the number of possible combinations if
(a) there is no restriction (i.e. the total number of combinations)
(b) both cards are ♦
(c) the cards are of the same suit
(d) the cards are ♦ and ♣
(e) the cards are of different suits
(f) the cards are of the same rank
(g) the ranks are consecutive (namely A2, 23, 34,…, QK, KA, regardless the suit)
▶️Answer/Explanation
Ans
(a) \(\binom{52}{2}=1326\) (b) \(\binom{13}{2}=78\)
(c) \(\binom{13}{2}\times 4=312\) (d) \(13^{2}=169\)
(e) \(either 13^{2}\times \binom{4}{2}=1014\) or \(1326-312=1014\)
(f) \(\binom{4}{2}\times 13=78\) (g) \(4^{2}\times 13=208\)
Question
There are 30 students in a class, of which 18 are girls and 12 are boys. Four students are selected at random to form a committee. Calculate
(a) the total number of possible committees
(b) the number of possible committees so that two girls and two boys are selected;
(c) the number of possible committees with students all of the same gender.
▶️Answer/Explanation
Ans
(a) Total number of ways of selecting 4 from 30 =\(\binom{30}{4}\)
(b) Number of ways of choosing \(2B\ 2G\binom{12}{2}\binom{18}{2}\)
(c) Number of ways of choosing \(4B=\binom{12}{4}\), choosing \(4G=\binom{18}{4}\)
Total number = \(\binom{12}{4}+\binom{18}{4}\)
Question
A team of five students is to be chosen at random to take part in a debate. The team is to be chosen from a group of eight medical students and three law students. Find the number of all
possible ways
(a) if there is no restriction for the subject of the students
(b) that only medical students are chosen;
(c) that all three law students are chosen;
▶️Answer/Explanation
Ans
(a) \(\binom{11}{5}=462\)
(b) \(\binom{8}{5}=56\)
(c) \\binom{3}{3}\binom{8}{2}=28\) (corresponding probability \(28/462 = 2/33)\)
Question
A room has nine desks arranged in three rows of three desks. Three students sit in the room. If the students randomly choose a desk find
(a) the number of ways that three desks may be chosen
(b) the number of ways that three desks may be chosen so that two out of the front three desks are included.
▶️Answer/Explanation
Ans
(a) \(9C3\)
(b) \(3C2\times 6C1\)
Extra question
Find the number of ways the 3 students can sit in each case above
Ans
each answer above must be multiplied by \(3!=6\)
Question
A committee of four children is chosen from eight children. The two oldest children cannot both be chosen. Find the number of ways the committee may be chosen.
▶️Answer/Explanation
Ans
METHOD 1
Consider two groups – one group of the two oldest, one group of the rest
Either one of the two oldest is chosen or neither is chosen
Then the number of ways to choose the committee is
\(\binom{6}{3}\binom{2}{1}+\binom{6}{4}\binom{2}{0}=40+15=55\) ways
METHOD 2
Total number minus the number of ways to have both the oldest \(\Rightarrow \)
\(\binom{8}{4}-\binom{6}{2}=70-15=55\) ways
Question
In how many ways can six different coins be divided between two students so that each student receives at least one coin?
▶️Answer/Explanation
Ans
The first student can receive \(x\) coins in \(\binom{6}{x}\) ways, \(1\leq x\leq 5\).
[The second student then receives the rest.]
Therefore, the number of ways = \(\binom{6}{1}+\binom{6}{2}+\binom{6}{3}+\binom{6}{4}+\binom{6}{5}=2^{6}-2=62\).
Question
There are six boys and five girls in a school tennis club. A team of two boys and two girls will be selected to represent the school in a tennis competition.
(a) In how many different ways can the team be selected?
(b) Tim is the youngest boy in the club and Anna is the youngest girl. In how many different ways can the team be selected if it must include both of them?
(c) Fred is the oldest boy in the club. Given that Fred is selected for the team, in how many different ways can the team be selected if it must include Tim or Anna, but not both?
▶️Answer/Explanation
Ans
(a) Boys can be chosen in \(\frac{6\times5 }{2}=15\) ways
Girls can be chosen in \(\frac{5\times 4}{2}=10\) ways
Total = \(15\times 10=150 ways\)
(b) Number of ways = \(5\times 4=20\)
(c) Number of selections including Tim but not Anna = \(\binom{4}{2}=6\)
Number of selections including Anna but not Tim = \(4\times 4=16\)
Number of selections including Anna or Tim but not both = \(6+16=22\)
Question
Twelve people travel in three cars, with four people in each car. Each car is driven by its owner. Find the number of ways in which the remaining nine people may be allocated to the cars. (The
arrangement of people within a particular car is not relevant).
▶️Answer/Explanation
Ans
The first car can be filled in \(_{}^{9}\textrm{C}_{3}\) ways.
The second car can be filled in \(_{}^{6}\textrm{C}_{3}\) ways.
The third car can be filled in \(_{}^{3}\textrm{C}_{3}\) ways.
Number of combinations = \(_{}^{9}\textrm{C}_{3}\times _{}^{6}\textrm{C}_{3}\times_{}^{3}\textrm{C}_{3}=84\times 20\times 1=1680\).
Question
There are 10 seats in a row in a waiting room. There are six people in the room.
(a) In how many different ways can they be seated?
(b) In the group of six people, there are three sisters who must sit next to each other. In how many different ways can the group be seated?
▶️Answer/Explanation
Ans
(a) A recognition of a permutation of six from ten in words or symbols
Total number of ways = \(151200\)
(b) Total number of ways = \(8\times 3!\times 7\times 6\times 5=10080\)
Question
Mr Blue, Mr Black, Mr Green, Mrs White, Mrs Yellow and Mrs Red sit around a circular table for a meeting. Mr Black and Mrs White must not sit together.
Calculate the number of different ways these six people can sit at the table without Mr Black and Mrs White sitting together.
METHOD A (directly)
▶️Answer/Explanation
Ans
If Mr Black is seated, then Mrs White has 3 choices.
\(4!\) is the number of different ways the remaining 4 people can sit around a circular table.
Therefore the number of different ways is \(3 × 4! = 72\).
OR
METHOD B (indirectly: calculate the total number and subtract the opposite)
Ans
The number of different ways six people can sit around a circular table is \(5! = 120\).
The number of different ways these six people can sit around a circular table with Mr Black and Mrs White together is \(4! × 2 = 48\).
Therefore, the number of different ways in question is \(120 – 48 = 72\)
Question
How many four-digit numbers are there which contain at least one digit 3?
▶️Answer/Explanation
Ans
The total number of four-digit numbers = \(9 × 10 × 10 × 10 = 9000\).
The number of four-digit numbers which do not contain a digit \(3 = 8 × 9 × 9 × 9 = 5832\).
Thus, the number of four-digit numbers which contain at least one digit \(3\) is \(9000 – 5832 = 3168\).
Question
Three Mathematics books, five English books, four Science books and a dictionary are to be placed on a student’s shelf so that the books of each subject remain together.
(a) In how many different ways can the books be arranged?
(b) In how many of these will the dictionary be next to the Mathematics books?
▶️Answer/Explanation
Ans
(a) There are \(3!\) ways of arranging the Mathematics books, \(5!\) ways of arranging the English books and \(4!\) ways of arranging the Science books.
Then we have \(4\) types of books which can be arranged in \(4!\) ways.
\(3! × 5! × 4 × 4! = 414720\)
(b) There are \(3!\) ways of arranging the subject books, and for each of these there are \(2\) ways of putting the dictionary next to the Mathematics books.
\(3! × 5! × 4! × 3! × 2 = 207 360\)
Question
There is a team of ten people working on a building, including three electricians and two plumbers. The architect called a meeting with five of the team, and randomly selected people to attend.
Calculate the probability that exactly two electricians and one plumber were called to the meeting.
▶️Answer/Explanation
Ans
Probability of \(2\) electricians and \(1\) plumber = \(\frac{\binom{3}{2}\binom{2}{1}\binom{5}{2}}{\binom{10}{5}}=\frac{60}{252}\left ( =\frac{5}{21}=0.238 \right )\)
OR
Probability of \(2\) electricians and \(1\) plumber = \(\frac{5!}{2!2!}\left ( \frac{3}{10} \right )\left ( \frac{2}{9} \right )\left ( \frac{2}{8} \right )\left ( \frac{5}{7} \right )\left ( \frac{4}{6} \right )=\frac{5}{21}(=0.238)\)
Question
A deck of 52 playing cards consists of
4 suits (♠,♣,♥,♦),
of 13 ranks each (A,2,3,4,5,6,7,8,9,10,J,Q,K)
When playing poker, we select five cards.
Confirm the following numbers of winning combinations by using techniques of counting.
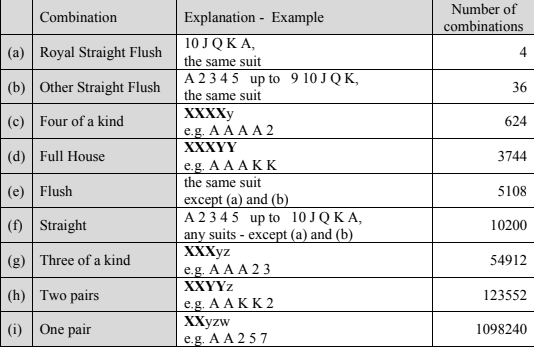
Notice: The number of all possible combinations is \(\binom{52}{5}=2598960\)
If you divide each result by the total number \(2598960\), you may also find the probability of the corresponding combination.
▶️Answer/Explanation
Ans
The final answers are given in the question.