Question
At Nusaybah’s Breakfast Diner, three types of omelette are available to order: chicken, vegetarian and steak. Each omelette is served with either a portion of fries or hash browns. It is known that 20 % of customers choose a chicken omelette, 70 % choose a vegetarian omelette and 10 % choose a steak omelette.
It is also known that 65% of those ordering the chicken omelette, 70 % of those ordering the vegetarian omelette and 60 % of those ordering the steak omelette, order fries.
The following tree diagram represents the orders made by each customer.
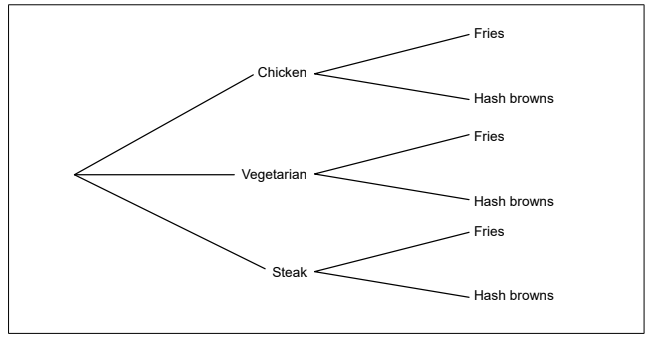
Complete the tree diagram by adding the respective probabilities to each branch. [2]
Find the probability that a randomly selected customer orders fries. [2]
Find the probability that a randomly selected customer orders fries, given that they do [Maximum mark: 7]
Answer/Explanation
Ans:
(a)
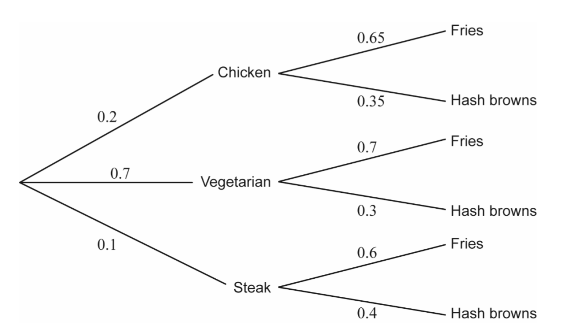
(b) (0.2 × 0.5)+(0.7 × 0.7)+(0.1× 0.6)= 0.68 \((=\frac{17}{25})\)
(c)
Question
Let A and B be events such that \({\text{P}}(A) = 0.6,{\text{ P}}(A \cup B) = 0.8{\text{ and P}}(A|B) = 0.6\) .
Find P(B) .
Answer/Explanation
Markscheme
EITHER
Using \({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\(0.6{\text{P}}(B) = {\text{P}}(A \cap B)\) A1
Using \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) to obtain \(0.8 = 0.6 + {\text{P}}(B) – {\text{P}}(A \cap B)\) A1
Substituting \(0.6{\text{P}}(B) = {\text{P}}(A \cap B)\) into above equation M1
OR
As \({\text{P}}(A|B) = {\text{P}}(A)\) then A and B are independent events M1R1
Using \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A) \times {\text{P}}(B)\) A1
to obtain \(0.8 = 0.6 + {\text{P}}(B) – 0.6 \times {\text{P}}(B)\) A1
THEN
\(0.8 = 0.6 + 0.4{\text{P}}(B)\) A1
\({\text{P}}(B) = 0.5\) A1 N1
[6 marks]
Examiners report
This question was generally well done, with a few candidates spotting an opportunity to use results for the independent events A and B.
Question
Events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.4\) .
Find the value of \({\text{P}}(A \cup B)\) when
(i) \(A\) and \(B\) are mutually exclusive;
(ii) \(A\) and \(B\) are independent.
Given that \({\text{P}}(A \cup B) = 0.6\) , find \({\text{P}}(A|B)\) .
Answer/Explanation
Markscheme
(i) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) = 0.7\) A1
(ii) \({\text{P}}(A \cup B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cap B)\) (M1)
\( = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A){\text{P}}(B)\) (M1)
\( = 0.3 + 0.4 – 0.12 = 0.58\) A1
[4 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) + {\text{P}}(B) – {\text{P}}(A \cup B)\)
\( = 0.3 + 0.4 – 0.6 = 0.1\) A1
\({\text{P}}(A|B) = \frac{{{\text{P}}(A \cap B)}}{{{\text{P}}(B)}}\) (M1)
\( = \frac{{0.1}}{{0.4}} = 0.25\) A1
[3 marks]
Examiners report
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Most candidates attempted this question and answered it well. A few misconceptions were identified (eg \({\text{P}}(A \cup B) = {\text{P}}(A){\text{P}}(B)\) ). Many candidates were unsure about the meaning of independent events.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
Draw a tree diagram to represent these events and their outcomes.
What is the probability that the “Tigers” soccer team wins?
Given that the “Tigers” soccer team won, what is the probability that it rained on that day?
Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”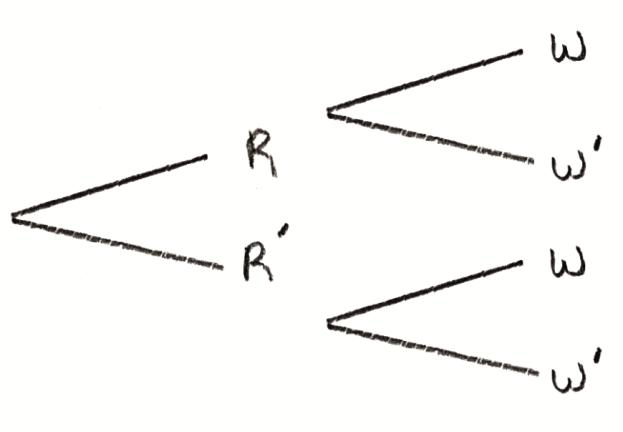
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
On a particular day, the probability that it rains is \(\frac{2}{5}\) . The probability that the “Tigers” soccer team wins on a day when it rains is \(\frac{2}{7}\) and the probability that they win on a day when it does not rain is \(\frac{4}{7}\).
Draw a tree diagram to represent these events and their outcomes.
What is the probability that the “Tigers” soccer team wins?
Given that the “Tigers” soccer team won, what is the probability that it rained on that day?
Answer/Explanation
Markscheme
let R be “it rains” and W be “the ‘Tigers’ soccer team win”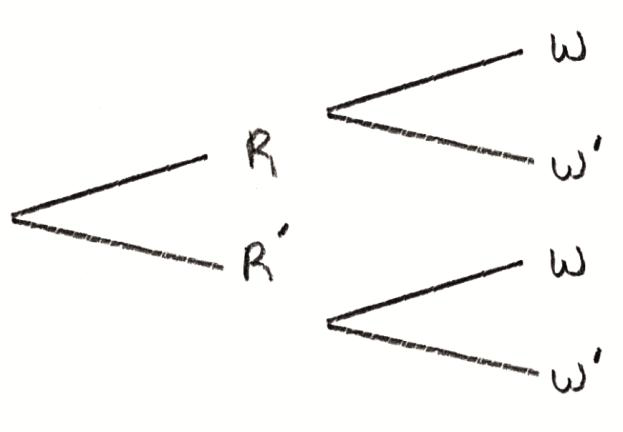
A1
[1 mark]
\({\text{P}}(W) = \frac{2}{5} \times \frac{2}{7} + \frac{3}{5} \times \frac{4}{7}\) (M1)
\( = \frac{{16}}{{35}}\) A1
[2 marks]
\({\text{P}}(R\left| W \right.) = \frac{{\frac{2}{5} \times \frac{2}{7}}}{{\frac{{16}}{{35}}}}\) (M1)
\( = \frac{1}{4}\) A1
[2 marks]
Examiners report
This question was well answered in general.
This question was well answered in general.
This question was well answered in general.
Question
Consider the following functions:
\[f(x) = \frac{{2{x^2} + 3}}{{75}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{{\left| {3x – 4} \right|}}{{10}},{\text{ }}x \in \mathbb{R}{\text{ }}.\]
State the range of f and of g .
Find an expression for the composite function \(f \circ g(x)\) in the form \(\frac{{a{x^2} + bx + c}}{{3750}}\), where \(a,{\text{ }}b{\text{ and }}c \in \mathbb{Z}\) .
(i) Find an expression for the inverse function \({f^{ – 1}}(x)\) .
(ii) State the domain and range of \({f^{ – 1}}\) .
The domains of f and g are now restricted to {0, 1, 2, 3, 4} .
By considering the values of f and g on this new domain, determine which of f and g could be used to find a probability distribution for a discrete random variable X , stating your reasons clearly.
Using this probability distribution, calculate the mean of X .
Answer/Explanation
Markscheme
\(f(x) \geqslant \frac{1}{{25}}\) A1
\(g(x) \in \mathbb{R},{\text{ }}g(x) \geqslant 0\) A1
[2 marks]
\(f \circ g(x) = \frac{{2{{\left( {\frac{{3x – 4}}{{10}}} \right)}^2} + 3}}{{75}}\) M1A1
\( = \frac{{\frac{{2(9{x^2} – 24x + 16)}}{{100}} + 3}}{{75}}\) (A1)
\( = \frac{{9{x^2} – 24x + 166}}{{3750}}\) A1
[4 marks]
(i) METHOD 1
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\({x^2} = \frac{{75y – 3}}{2}\) M1
\(x = \sqrt {\frac{{75y – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
METHOD 2
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\(x = \frac{{2{y^2} + 3}}{{75}}\) M1
\(y = \sqrt {\frac{{75x – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
(ii) domain: \(x \geqslant \frac{1}{{25}}\) ; range: \({f^{ – 1}}(x) \geqslant 0\) A1
[4 marks]
probabilities from \(f(x)\) :
A2
Note: Award A1 for one error, A0 otherwise.
probabilities from \(g(x)\) :
A2
Note: Award A1 for one error, A0 otherwise.
only in the case of \(f(x)\) does \(\sum {P(X = x) = 1} \) , hence only \(f(x)\) can be used as a probability mass function A2
[6 marks]
\(E(x) = \sum {x \cdot {\text{P}}(X = x)} \) M1
\( = \frac{5}{{75}} + \frac{{22}}{{75}} + \frac{{63}}{{75}} + \frac{{140}}{{75}} = \frac{{230}}{{75}}\left( { = \frac{{46}}{{15}}} \right)\) A1
[2 marks]
Examiners report
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
Question
Tim and Caz buy a box of 16 chocolates of which 10 are milk and 6 are dark. Caz randomly takes a chocolate and eats it. Then Tim randomly takes a chocolate and eats it.
Draw a tree diagram representing the possible outcomes, clearly labelling each branch with the correct probability.
Find the probability that Tim and Caz eat the same type of chocolate.
Answer/Explanation
Markscheme
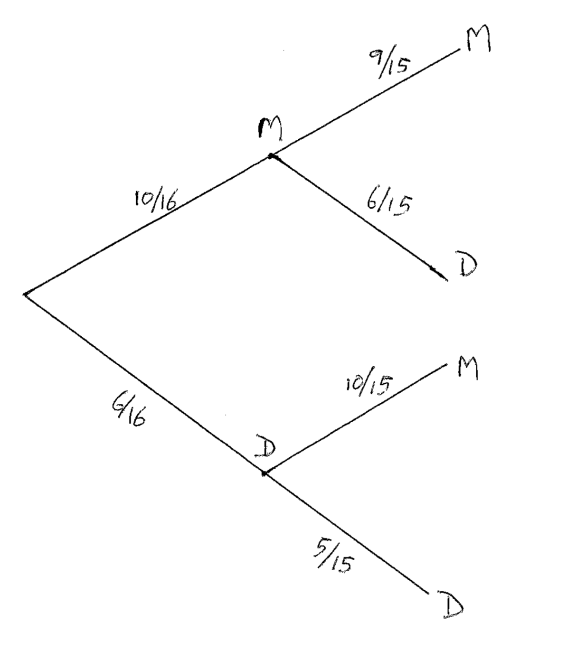A1A1A1
[3 marks]
Note: Award A1 for the initial level probabilities, A1 for each of the second level branch probabilities.
\(\frac{{10}}{{16}} \times \frac{9}{{15}} + \frac{6}{{16}} \times \frac{5}{{15}}\) (M1)
\( = \frac{{120}}{{240}}{\text{ }}\left( { = \frac{1}{2}} \right)\) A1
[2 marks]
Examiners report
Generally well done. A few candidates didn’t take account of the fact that Caz ate the chocolate, so didn’t replace it. A few candidates made arithmetic errors in calculating the probability.
Generally well done. A few candidates didn’t take account of the fact that Caz ate the chocolate, so didn’t replace it. A few candidates made arithmetic errors in calculating the probability.
Question
A box contains four red balls and two white balls. Darren and Marty play a game by each taking it in turn to take a ball from the box, without replacement. The first player to take a white ball is the winner.
Darren plays first, find the probability that he wins.
The game is now changed so that the ball chosen is replaced after each turn.
Darren still plays first.
Show that the probability of Darren winning has not changed.
Answer/Explanation
Markscheme
probability that Darren wins \({\text{P}}(W) + {\text{P}}(RRW) + {\text{P}}(RRRRW)\) (M1)
Note: Only award M1 if three terms are seen or are implied by the following numerical equivalent.
Note: Accept equivalent tree diagram for method mark.
\( = \frac{2}{6} + \frac{4}{6} \bullet \frac{3}{5} \bullet \frac{2}{4} + \frac{4}{6} \bullet \frac{3}{5} \bullet \frac{2}{4} \bullet \frac{1}{3} \bullet \frac{2}{2}\;\;\;\left( { = \frac{1}{3} + \frac{1}{5} + \frac{1}{{15}}} \right)\) A2
Note: A1 for two correct.
\( = \frac{3}{5}\) A1
[4 marks]
METHOD 1
the probability that Darren wins is given by
\({\text{P}}(W) + {\text{P}}(RRW) + {\text{P}}(RRRRW) + \ldots \) (M1)
Note: Accept equivalent tree diagram with correctly indicated path for method mark.
\({\text{P (Darren Win)}} = \frac{1}{3} + \frac{2}{3} \bullet \frac{2}{3} \bullet \frac{1}{3} + \frac{2}{3} \bullet \frac{2}{3} \bullet \frac{2}{3} \bullet \frac{2}{3} \bullet \frac{1}{3} + \ldots \)
or \( = \frac{1}{3}\left( {1 + \frac{4}{9} + {{\left( {\frac{4}{9}} \right)}^2} + \ldots } \right)\) A1
\( = \frac{1}{3}\left( {\frac{1}{{1 – \frac{4}{9}}}} \right)\) A1
\( = \frac{3}{5}\) AG
METHOD 2
\({\text{P (Darren wins)}} = {\text{P}}\)
\({\text{P}} = \frac{1}{3} + \frac{4}{9}{\text{P}}\) M1A2
\(\frac{5}{9}{\text{P}} = \frac{1}{3}\)
\({\text{P}} = \frac{3}{5}\) AG
[3 marks]
Total [7 marks]
Examiners report
[N/A]
[N/A]