Question
At a school, 70 % of the students play a sport and 20 % of the students are involved in theatre. 18 % of the students do neither activity.
A student is selected at random.
(a) Find the probability that the student plays a sport and is involved in theatre. [2]
(b) Find the probability that the student is involved in theatre, but does not play a sport. [2]
At the school 48 % of the students are girls, and 25 % of the girls are involved in theatre.
A student is selected at random. Let G be the event “the student is a girl” and let T be the event “the student is involved in theatre”.
(c) Find P (G ∩ T ) . [2]
(d) Determine if the events G and T are independent. Justify your answer. [2]
▶️Answer/Explanation
Ans:
(a) By using the combined events formula, we have $\begin{eqnarray} \text{P}\left(S\cup T\right) = \text{P}\left(S\right)+\text{P}\left(T\right)-\text{P}\left(S\cap T\right) \nonumber \\ 0.82 = 0.7+0.2-\text{P}\left(S\cap T\right) \nonumber \\ \text{P}\left(S\cap T\right) = 0.08. \end{eqnarray}$ (b) $\begin{eqnarray} \text{P}\left(T\cap S’\right) &=& \text{P}\left(t\right)-\text{P}\left(S\cap T\right) \nonumber \\ &=& 0.2-0.08 \nonumber \\ &=& 0.12. \end{eqnarray}$ (c) $\begin{eqnarray} \text{P}\left(G\cap T\right) &=& 0.48\times 0.25 \nonumber \\ &=& 0.12. \end{eqnarray}$ (d) Since $\begin{eqnarray} \text{P}\left(G\right)\times\text{P}\left(T\right) &=& 0.48\times 0.2 \nonumber \\ &=& 0.096 \nonumber \\ &\neq & 0.12 \nonumber \\ &=& \text{P}\left(G\cap T\right), \end{eqnarray}$ $G$ and $T$ are not independent.
Question
(a) A box of biscuits is considered to be underweight if it weighs less than 228 grams. It is known that the weights of these boxes of biscuits are normally distributed with a mean of 231 grams and a standard deviation of 1.5 grams.
What is the probability that a box is underweight?
(b) The manufacturer decides that the probability of a box being underweight should be reduced to 0.002.
(i) Bill’s suggestion is to increase the mean and leave the standard deviation unchanged. Find the value of the new mean.
(ii) Sarah’s suggestion is to reduce the standard deviation and leave the mean unchanged. Find the value of the new standard deviation.
(c) After the probability of a box being underweight has been reduced to 0.002, a group of customers buys 100 boxes of biscuits. Find the probability that at least two of the boxes are underweight.[11]
There are six boys and five girls in a school tennis club. A team of two boys and two girls will be selected to represent the school in a tennis competition.
(a) In how many different ways can the team be selected?
(b) Tim is the youngest boy in the club and Anna is the youngest girl. In how many different ways can the team be selected if it must include both of them?
(c) What is the probability that the team includes both Tim and Anna?
(d) Fred is the oldest boy in the club. Given that Fred is selected for the team, what is the probability that the team includes Tim or Anna, but not both?[10]
▶️Answer/Explanation
Markscheme
(a) \(X \sim {\text{N(231, 1.}}{{\text{5}}^2})\)
\({\text{P}}(X < 228) = 0.0228\) (M1)A1
Note: Accept 0.0227.
[2 marks]
(b) (i) \(X \sim {\text{N(}}\mu {\text{, 1.}}{{\text{5}}^2})\)
\({\text{P}}(X < 228) = 0.002\)
\(\frac{{228 – \mu }}{{1.5}} = – 2.878…\) M1A1
\(\mu = 232{\text{ grams}}\) A1 N3
(ii) \(X \sim {\text{N(231, }}{\sigma ^2})\)
\(\frac{{228 – 231}}{\sigma } = – 2.878…\) M1A1
\(\sigma = 1.04{\text{ grams}}\) A1 N3
[6 marks]
(c) \(X \sim {\text{B(100, 0.002)}}\) (M1)
\({\text{P}}(X \leqslant 1) = 0.982…\) (A1)
\({\text{P}}(X \geqslant 2) = 1 – {\text{P}}(X \leqslant 1) = 0.0174\) A1
[3 marks]
Total [11 marks]
(a) Boys can be chosen in \(\frac{{6 \times 5}}{2} = 15\) ways (A1)
Girls can be chosen in \(\frac{{5 \times 4}}{2} = 10\) ways (A1)
Total \( = 15 \times 10 = 150\) ways A1
[3 marks]
(b) Number of ways \( = 5 \times 4 = 20\) (M1)A1
[2 marks]
(c) \(\frac{{20}}{{150}}{\text{ }}\left( { = \frac{2}{{15}}} \right)\) A1
[1 mark]
(d) METHOD 1
\({\text{P}}(T) = \frac{1}{5};{\text{ P}}(A) = \frac{2}{5}\) A1
P(T or A but not both) \( = {\text{P}}(T) \times {\text{P}}(A’) + {\text{P}}(T’) \times {\text{P}}(A)\) M1A1
\( = \frac{1}{5} \times \frac{3}{5} + \frac{4}{5} \times \frac{2}{5} = \frac{{11}}{{25}}\) A1
METHOD 2
Number of selections including Fred \( = 5 \times \left( {\begin{array}{*{20}{c}}
5 \\
2
\end{array}} \right) = 50\) A1
Number of selections including Tim but not Anna \( = \left( {\begin{array}{*{20}{c}}
4 \\
2
\end{array}} \right) = 6\) A1
Number of selections including Anna but not Tim \( = 4 \times 4 = 16\)
Note: Both statements are needed to award A1.
P(T or A but not both) \( = \frac{{6 + 16}}{{50}} = \frac{{11}}{{25}}\) M1A1
[4 marks]
Total [10 marks]
Question
In a class of \(20\) students, \(12\) study Biology, \(15\) study History and \(2\) students study neither Biology nor History.
(a) Illustrate this information on a Venn diagram.
(b) Find the probability that a randomly selected student from this class is studying both Biology and History.
(c) Given that a randomly selected student studies Biology, find the probability that this student also studies History.
▶️Answer/Explanation
Markscheme
(a)
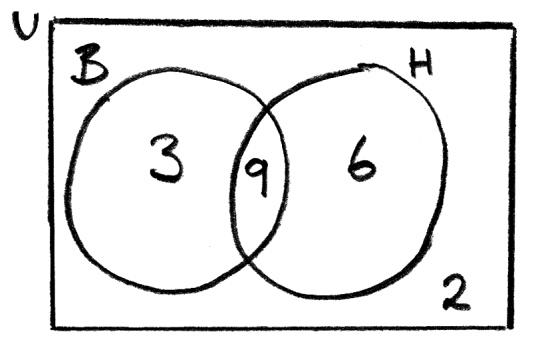A1A1
Note: Award A1 for a diagram with two intersecting regions and at least the value of the intersection.
(b) \(\frac{9}{{20}}\) A1
(c) \(\frac{9}{{12}}\left( { = \frac{3}{4}} \right)\) A1
[4 marks]
Question
(a) Find the percentage of the population that has been vaccinated.
(b) A randomly chosen person catches the virus. Find the probability that this person has been vaccinated.
▶️Answer/Explanation
Markscheme
(a)
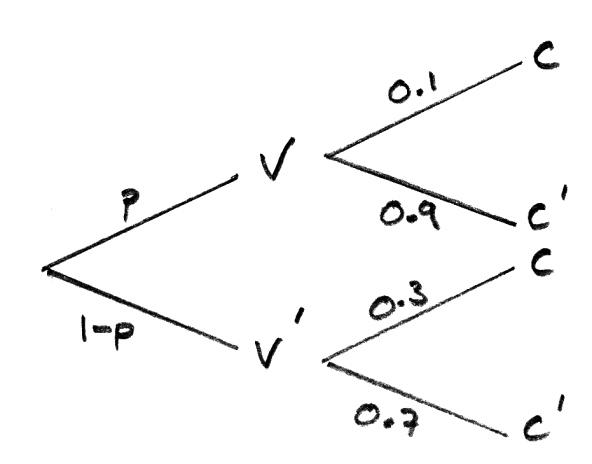
using the law of total probabilities: (M1)
\(0.1p + 0.3\left( {1 – p} \right) = 0.22\) A1
\(0.1p + 0.3 – 0.3p = 0.22\)
\(0.2p = 0.88\)
\(p = \frac{{0.88}}{{0.2}} = 0.4\)
\(p = 40\% \) (accept \(0.4\)) A1
(b) required probability \( = \frac{{0.4 \times 0.1}}{{0.22}}\) M1
\( = \frac{2}{{11}}\) (\(0.182\)) A1
[5 marks]
Question
In each round of two different games Ying tosses three fair coins and Mario tosses two fair coins.
(a) The first game consists of one round. If Ying obtains more heads than Mario, she receives $5 from Mario. If Mario obtains more heads than Ying, he receives $10 from Ying. If they obtain the same number of heads, then Mario receives $2 from Ying. Determine Ying’s expected winnings.
(b) They now play the second game, where the winner will be the player who obtains the larger number of heads in a round. If they obtain the same number of heads, they play another round until there is a winner. Calculate the probability that Ying wins the game.
▶️Answer/Explanation
Markscheme
(a) Ying:
(M1)A1
Mario:
(M1)A1
\({\text{P(Ying wins)}} = \frac{1}{8} + \frac{3}{8}\left( {\frac{2}{4} + \frac{1}{4}} \right) + \frac{3}{8} \times \frac{1}{4}\)
\( = \frac{{16}}{{32}}\) (M1)A1
\({\text{P(Mario wins)}} = \frac{1}{4}\left( {\frac{3}{8} + \frac{1}{8}} \right) + \frac{2}{4} \times \frac{1}{8}\)
\( = \frac{6}{{32}}\) (M1)A1
\({\text{P(draw)}} = 1 – \frac{{16}}{{32}} – \frac{6}{{32}}\)
\( = \frac{{10}}{{32}}\) A1
Ying’s winnings:
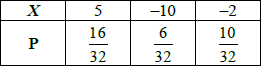
expected winnings \( = 5\left( {\frac{{16}}{{32}}} \right) – 105\left( {\frac{6}{{32}}} \right) – 25\left( {\frac{{10}}{{32}}} \right)\) M1A1
\( = 0\) A1
[12 marks]
(b) \({\text{P(Ying wins on 1st round)}} = \frac{1}{2}\) (A1)
\({\text{P(Ying wins on 2st round)}} = \frac{5}{{16}} \times \frac{1}{2}\) (M1)(A1)
\({\text{P(Ying wins on 3rd round)}} = {\left( {\frac{5}{{16}}} \right)^2} \times \frac{1}{2}\) etc. (A1)
\({\text{P(Ying wins)}} = \frac{1}{2} + \frac{5}{{16}} \times \frac{1}{2} + {\left( {\frac{5}{{16}}} \right)^2} \times \frac{1}{2} + …\) (M1)
\( = \frac{{\frac{1}{2}}}{{1 – \frac{5}{{16}}}}\) M1A1
\( = \frac{8}{{11}}\) ( \( =0.727\)) A1
[8 marks]
Total [20 marks]
Question
A team of 6 players is to be selected from 10 volleyball players, of whom 8 are boys and 2 are girls.
a.In how many ways can the team be selected?[2]
b.In how many of these selections is exactly one girl in the team?[3]
c.If the selection of the team is made at random, find the probability that exactly one girl is in the team.[2]
▶️Answer/Explanation
Markscheme
\(\left( {\begin{array}{*{20}{c}}
{10} \\
6
\end{array}} \right) = 210\) (M1)A1
[2 marks]
\(2 \times \left( {\begin{array}{*{20}{c}}
8 \\
5
\end{array}} \right) = 112\) (M1)A1A1
Note: Accept \(210 – 28 – 70 = 112\)
[3 marks]
\(\frac{{112}}{{210}}\,\,\left( { = \frac{8}{{15}} = 0.533} \right)\) (M1)A1
[2 marks]
Question
At the start of each week, Eric and Marina pick a night at random on which they will watch a movie.
If they choose a Saturday night, the probability that they watch a French movie is \(\frac{7}{9}\) and if they choose any other night the probability that they watch a French movie is \(\frac{4}{9}\).
▶️Answer/Explanation
Markscheme
\({\text{P}}(F) = \left( {\frac{1}{7} \times \frac{7}{9}} \right) + \left( {\frac{6}{7} \times \frac{4}{9}} \right)\) (M1)(A1)
Note: Award M1 for the sum of two products.
\( = \frac{{31}}{{63}}{\text{ }}( = 0.4920 \ldots )\) A1
[3 marks]
Use of \({\text{P}}(S|F) = \frac{{{\text{P}}(S \cap F)}}{{{\text{P}}(F)}}\) to obtain \({\text{P}}(S|F) = \frac{{\frac{1}{7} \times \frac{7}{9}}}{{\frac{{31}}{{63}}}}\). M1
Note: Award M1 only if the numerator results from the product of two probabilities.
\( = \frac{7}{{31}}{\text{ }}( = 0.2258 \ldots )\) A1
[2 marks]
Question
Josie has three ways of getting to school. \(30\% \) of the time she travels by car, \(20\% \) of the time she rides her bicycle and \(50\% \) of the time she walks.
When travelling by car, Josie is late \(5\% \) of the time. When riding her bicycle she is late \(10\% \) of the time. When walking she is late \(25\% \) of the time. Given that she was on time, find the probability that she rides her bicycle.
▶️Answer/Explanation
Markscheme
EITHER
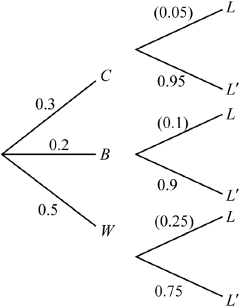M1A1A1
Note: Award M1 for a two-level tree diagram, A1 for correct first level probabilities, and A1 for correct second level probabilities.
OR
\({\text{P}}(B|L’) = \frac{{{\text{P}}(L’|B){\text{P}}(B)}}{{{\text{P}}(L’|B){\text{P}}(B) + {\text{P}}(L’|C){\text{P}}(C) + {\text{P}}(L’|W){\text{P}}(Q)}}\;\;\;\left( { = \frac{{{\text{P}}(B \cap L’}}{{{\text{P}}(L’)}}} \right)\) (M1)(A1)(A1)
THEN
\({\text{P}}(B|L’) = \frac{{0.9 \times 0.2}}{{0.9 \times 0.2 + 0.95 \times 0.3 + 0.75 \times 0.5}}\;\;\;\left( { = \frac{{0.18}}{{0.84}}} \right)\) M1A1
\( = 0.214\;\;\;\left( { = \frac{3}{{14}}} \right)\) A1
[6 marks]