Question
At a nursing college, 80 % of incoming students are female. College records show that 70 % of the incoming females graduate and 90 % of the incoming males graduate. A student who graduates is selected at random. Find the probability that the student is male, giving your answer as a fraction in its lowest terms.
▶️Answer/Explanation
Markscheme
\({\text{P }}M|G = \frac{{{\text{P}}(M \cap G)}}{{{\text{P}}(G)}}\) (M1)
\( = \frac{{0.2 \times 0.9}}{{0.2 \times 0.9 + 0.8 \times 0.7}}\) M1A1A1
\( = \frac{{0.18}}{{0.74}}\)
\( = \frac{9}{{37}}\) A1
[5 marks]
Examiners report
Most candidates answered this question successfully. Some made arithmetic errors.
Question
Jenny goes to school by bus every day. When it is not raining, the probability that the bus is late is \(\frac{3}{{20}}\). When it is raining, the probability that the bus is late is \(\frac{7}{{20}}\). The probability that it rains on a particular day is \(\frac{9}{{20}}\). On one particular day the bus is late. Find the probability that it is not raining on that day.
▶️Answer/Explanation
Markscheme
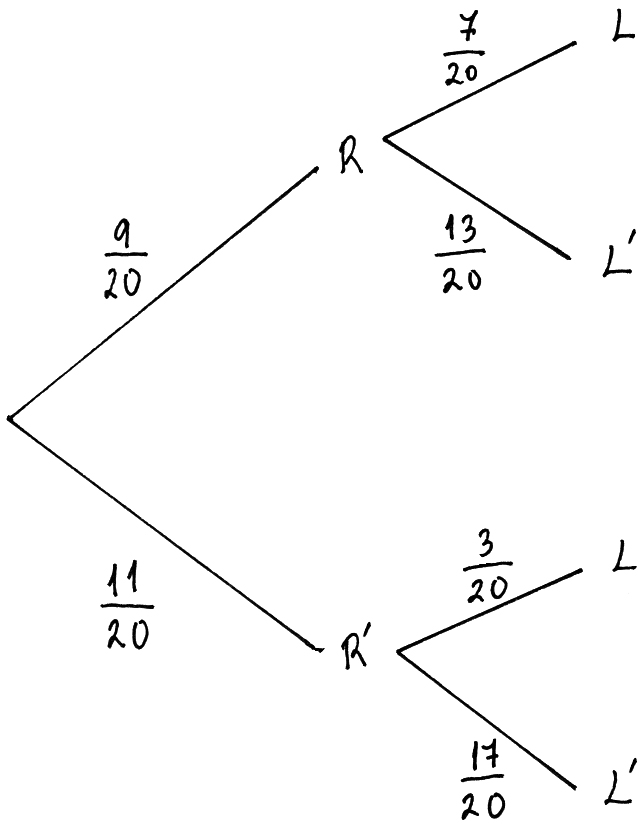 (A1)
(A1)
\({\text{P}}(R’ \cap L) = \frac{{11}}{{20}} \times \frac{3}{{20}}\) A1
\({\text{P}}(L) = \frac{9}{{20}} \times \frac{7}{{20}} + \frac{{11}}{{20}} \times \frac{3}{{20}}\) A1
\({\text{P}}(R’|L) = \frac{{{\text{P}}(R’ \cap L)}}{{{\text{P}}(L)}}\) (M1)
\( = \frac{{33}}{{96}}{\text{ }}\left( { = \frac{{11}}{{32}}} \right)\) A1
[5 marks]
Examiners report
This question was generally well answered with candidates who drew a tree diagram being the most successful.