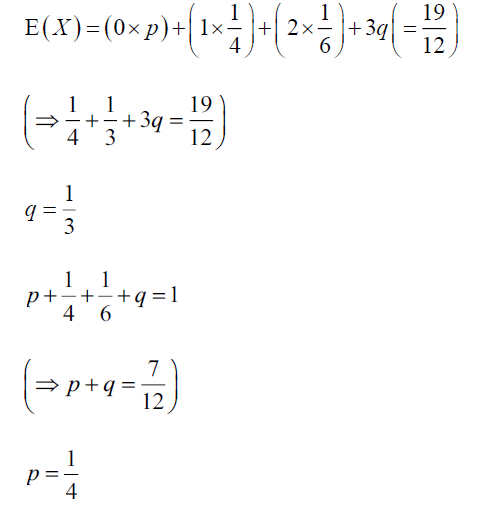Question
A discrete random variable X has the probability distribution given by the following table.
x | 0 | 1 | 2 | 3 |
P( X = x ) | p | \(\frac{1}{4}\) | \(\frac{1}{6}\) | q |
Given that E (X) = \(\frac{19}{12}\) , determine the value of p and the value of q .
Answer/Explanation
Ans:
Question
A biased four-sided die, A, is rolled. Let X be the score obtained when die A is rolled. The
probability distribution for X is given in the following table.
(a) Find the value of p . [2]
(b) Hence, find the value of E (X ) . [2]
A second biased four-sided die, B, is rolled. Let Y be the score obtained when die B is rolled.
The probability distribution for Y is given in the following table.
(c) (i) State the range of possible values of r .
(ii) Hence, find the range of possible values of q . [3]
(d) Hence, find the range of possible values for E (Y ) . [3]
Agnes and Barbara play a game using these dice. Agnes rolls die A once and Barbara rolls die B once. The probability that Agnes’ score is less than Barbara’s score is \(\frac{1}{2}\)
(e) Find the value of E (Y ) . [6]
Answer/Explanation
Ans

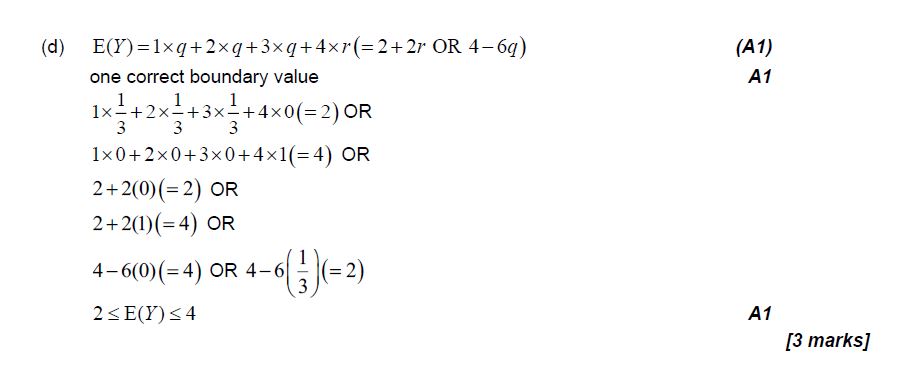


Question
The random variable T has the probability density function
\[f(t) = \frac{\pi }{4}\cos \left( {\frac{{\pi t}}{2}} \right),{\text{ }} – 1 \leqslant t \leqslant 1.\]
Find
(a) P(T = 0) ;
(b) the interquartile range.
Answer/Explanation
Markscheme
(a) Any consideration of \(\int_0^0 {f(x){\text{d}}x} \) (M1)
0 A1 N2
(b) METHOD 1
Let the upper and lower quartiles be a and −a
\(\frac{\pi }{4}\int_a^1 {\cos \frac{{\pi t}}{2}{\text{d}}t = 0.25} \) M1
\( \Rightarrow \left[ {\frac{\pi }{4} \times \frac{2}{\pi }\sin \frac{{\pi t}}{2}} \right]_a^1 = 0.25\) A1
\( \Rightarrow \left[ {\frac{1}{2}\sin \frac{{\pi t}}{2}} \right]_a^1 = 0.25\)
\( \Rightarrow \left[ {\frac{1}{2} – \frac{1}{2}\sin \frac{{\pi a}}{2}} \right] = 0.25\) A1
\( \Rightarrow \frac{1}{2}\sin \frac{{\pi a}}{2} = \frac{1}{4}\)
\( \Rightarrow \sin \frac{{\pi a}}{2} = \frac{1}{2}\)
\(\frac{{\pi a}}{2} = \frac{\pi }{6}\)
\(a = \frac{1}{3}\) A1
Since the function is symmetrical about t = 0 ,
interquartile range is \(\frac{1}{3} – \left( { – \frac{1}{3}} \right) = \frac{2}{3}\) R1
METHOD 2
\(\frac{\pi }{4}\int_{ – a}^a {\cos \frac{{\pi t}}{2}{\text{d}}t = 0.5 = \frac{\pi }{2}\int_0^a {\cos \frac{{\pi t}}{2}{\text{d}}t} } \) M1A1
\( \Rightarrow \left[ {\sin \frac{{a\pi }}{2}} \right] = 0.5\) A1
\( \Rightarrow \frac{{a\pi }}{2} = \frac{\pi }{6}\)
\( \Rightarrow a = \frac{1}{3}\) A1
The interquartile range is \(\frac{2}{3}\) R1
[7 marks]
Examiners report
All but the best candidates struggled with part (a). The vast majority either did not attempt it or let t = 1 . There was no indication from any of the scripts that candidates wasted an undue amount of time in trying to solve part (a). Many candidates attempted part (b), but few had a full understanding of the situation and hence were unable to give wholly correct answers.
Question
The probability distribution of a discrete random variable X is defined by
\({\text{P}}(X = x) = cx(5 – x),{\text{ }}x = {\text{1, 2, 3, 4}}\) .
(a) Find the value of c.
(b) Find E(X) .
Answer/Explanation
Markscheme
(a) Using \(\sum {{\text{P}}(X = x) = 1} \) (M1)
\(4c + 6c + 6c + 4c = 1\,\,\,\,\,(20c = 1)\) A1
\(c = \frac{1}{{20}}\,\,\,\,\,( = 0.05)\) A1 N1
(b) Using \({\text{E}}(X) = \sum {x{\text{P}}(X = x)} \) (M1)
\( = (1 \times 0.2) + (2 \times 0.3) + (3 \times 0.3) + (4 \times 0.2)\) (A1)
\( = 2.5\) A1 N1
Notes: Only one of the first two marks can be implied.
Award M1A1A1 if the x values are averaged only if symmetry is explicitly mentioned.
[6 marks]
Examiners report
This question was generally well done, but a few candidates tried integration for part (b).
Question
John removes the labels from three cans of tomato soup and two cans of chicken soup in order to enter a competition, and puts the cans away. He then discovers that the cans are identical, so that he cannot distinguish between cans of tomato soup and chicken soup. Some weeks later he decides to have a can of chicken soup for lunch. He opens the cans at random until he opens a can of chicken soup. Let Y denote the number of cans he opens.
Find
(a) the possible values of Y ,
(b) the probability of each of these values of Y ,
(c) the expected value of Y .
Answer/Explanation
Markscheme
(a) 1, 2, 3, 4 A1
(b) \({\text{P}}(Y = 1) = \frac{2}{5}\) A1
\({\text{P}}(Y = 2) = \frac{3}{5} \times \frac{2}{4} = \frac{3}{{10}}\) A1
\({\text{P}}(Y = 3) = \frac{3}{5} \times \frac{2}{4} \times \frac{2}{3} = \frac{1}{5}\) A1
\({\text{P}}(Y = 4) = \frac{3}{5} \times \frac{2}{4} \times \frac{1}{3} \times \frac{2}{2} = \frac{1}{{10}}\) A1
(c) \({\text{E}}(Y) = 1 \times \frac{2}{5} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{5} + 4 \times \frac{1}{{10}}\) M1
\( = 2\) A1
[7 marks]
Examiners report
Candidates found this question challenging with only better candidates gaining the correct answers. A number of students assumed incorrectly that the distribution was either Binomial or Geometric.
Question
The random variable X has probability density function f where
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{kx(x + 1)(2 – x),}&{0 \leqslant x \leqslant 2} \\
{0,}&{{\text{otherwise }}{\text{.}}}
\end{array}} \right.\]
Sketch the graph of the function. You are not required to find the coordinates of the maximum.
Find the value of k .
Answer/Explanation
Markscheme
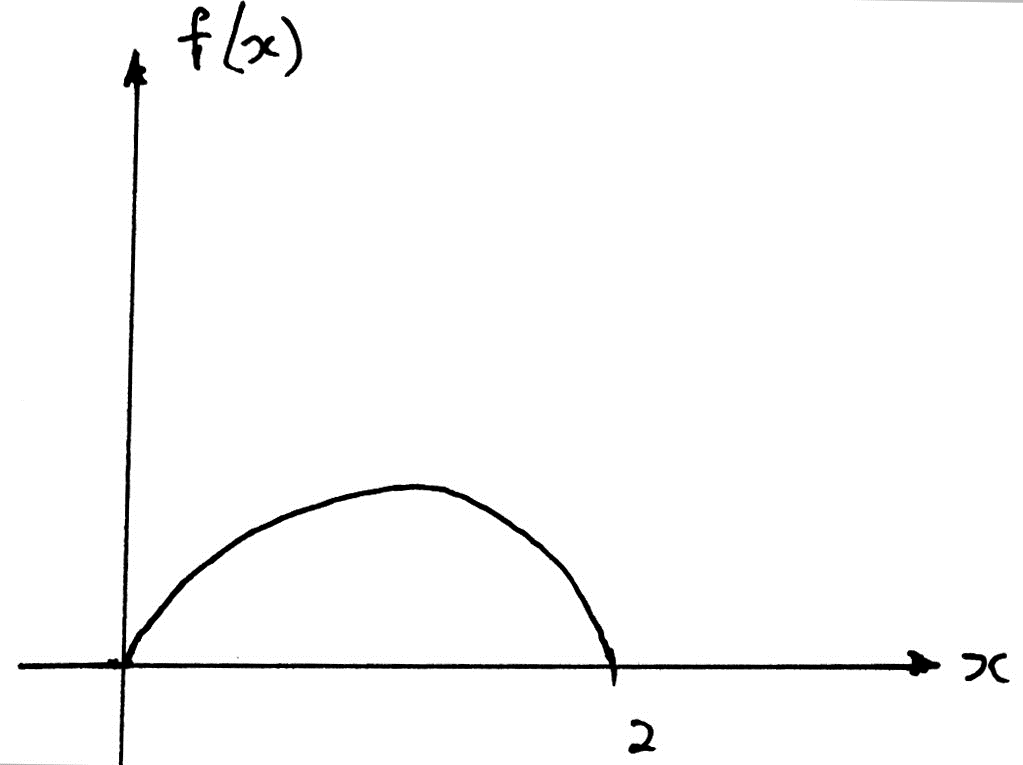 A1
A1
Note: Award A1 for intercepts of 0 and 2 and a concave down curve in the given domain .
Note: Award A0 if the cubic graph is extended outside the domain [0, 2] .
[1 mark]
\(\int_0^2 {kx(x + 1)(2 – x){\text{d}}x = 1} \) (M1)
Note: The correct limits and =1 must be seen but may be seen later.
\(k\int_0^2 {( – {x^3} + {x^2} + 2x){\text{d}}x = 1} \) A1
\(k\left[ { – \frac{1}{4}{x^4} + \frac{1}{3}{x^3} + {x^2}} \right]_0^2 = 1\) M1
\(k\left( { – 4 + \frac{8}{3} + 4} \right) = 1\) (A1)
\(k = \frac{3}{8}\) A1
[5 marks]
Examiners report
Most candidates completed this question well. A number extended the graph beyond the given domain.
Most candidates completed this question well. A number extended the graph beyond the given domain.
Question
A continuous random variable X has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k\sin x,}&{0 \leqslant x \leqslant \frac{\pi }{2}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the value of k.
Find \({\text{E}}(X)\).
Find the median of X.
Answer/Explanation
Markscheme
\(k\int_0^{\frac{\pi }{2}} {\sin x{\text{d}}x = 1} \) M1
\(k[ – \cos x]_0^{\frac{\pi }{2}} = 1\)
k = 1 A1
[2 marks]
\({\text{E}}(X) = \int_0^{\frac{\pi }{2}} {x\sin x{\text{d}}x} \) M1
integration by parts M1
\([ – x\cos x]_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {\cos x{\text{d}}x} \) A1A1
= 1 A1
[5 marks]
\(\int_0^M {\sin x{\text{d}}x} = \frac{1}{2}\) M1
\([ – \cos x]_0^M = \frac{1}{2}\) A1
\(\cos M = \frac{1}{2}\)
\(M = \frac{\pi }{3}\) A1
Note: accept \(\arccos \frac{1}{2}\)
[3 marks]
Examiners report
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Question
The discrete random variable X has probability distribution:

(a) Find the value of a.
(b) Find \({\text{E}}(X)\).
(c) Find \({\text{Var}}(X)\).
Answer/Explanation
Markscheme
(a) \(\frac{1}{6} + \frac{1}{2} + \frac{3}{{10}} + a = 1 \Rightarrow a = \frac{1}{{30}}\) A1
(b) \({\text{E}}(X) = \frac{1}{2} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{{30}}\) M1
\(= \frac{6}{5}\) A1
Note: Do not award FT marks if a is outside [0, 1].
[2 marks]
(c) \({\text{E}}({X^2}) = \frac{1}{2} + {2^2} \times \frac{3}{{10}} + {3^2} \times \frac{1}{{30}} = 2\) (A1)
attempt to apply \({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) M1
\(\left( { = 2 – \frac{{36}}{{25}}} \right) = \frac{{14}}{{25}}\) A1
[3 marks]
Total [6 marks]
Examiners report
This was very well answered and many fully correct solutions were seen. A small number of candidates made arithmetic mistakes in part a) and thus lost one or two accuracy marks. A few also seemed unaware of the formula \({\text{Var}}(X) = {\text{E}}({X^2}) – {\text{E}}{(X)^2}\) and resorted to seeking an alternative, sometimes even attempting to apply a clearly incorrect \({\text{Var}}(X) = \sum {{{({x_i} – \mu )}^2}} \).
Question
Find the coordinates of the point of intersection of the planes defined by the equations \(x + y + z = 3,{\text{ }}x – y + z = 5\) and \(x + y + 2z = 6\).
Answer/Explanation
Markscheme
METHOD 1
for eliminating one variable from two equations (M1)
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ {2x + 2z = 8} \\ {2x + 3z = 11} \end{array}} \right.\) A1A1
for finding correctly one coordinate
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ {(2x + 2z = 8)} \\ {z = 3} \end{array}} \right.\) A1
for finding correctly the other two coordinates A1
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 1} \\ {y = – 1} \\ {z = 3} \end{array}} \right.\)
the intersection point has coordinates \((1,{\text{ }} – 1,{\text{ }}3)\)
METHOD 2
for eliminating two variables from two equations or using row reduction (M1)
eg, \(\left\{ {\begin{array}{*{20}{l}} {(x + y + z = 3)} \\ { – 2 = 2} \\ {z = 3} \end{array}} \right.\) or \(\left( {\begin{array}{*{20}{c}} 1&1&1 \\ 0&{ – 2}&0 \\ 0&0&1 \end{array}\left| {\begin{array}{*{20}{c}} 3 \\ 2 \\ 3 \end{array}} \right.} \right)\) A1A1
for finding correctly the other coordinates A1A1
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}} {x = 1} \\ {y = – 1} \\ {(z = 3)} \end{array}} \right.\) or \(\left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&1&0 \\ 0&0&1 \end{array}\left| {\begin{array}{*{20}{c}} 1 \\ { – 1} \\ 3 \end{array}} \right.} \right)\)
the intersection point has coordinates \((1,{\text{ }} – 1,{\text{ }}3)\)
METHOD 3
\(\left| {\begin{array}{*{20}{c}} 1&1&1 \\ 1&{ – 1}&1 \\ 1&1&2 \end{array}} \right| = – 2\) (A1)
attempt to use Cramer’s rule M1
\(x = \frac{{\left| {\begin{array}{*{20}{c}} 3&1&1 \\ 5&{ – 1}&1 \\ 6&1&2 \end{array}} \right|}}{{ – 2}} = \frac{{ – 2}}{{ – 2}} = 1\) A1
\(y = \frac{{\left| {\begin{array}{*{20}{c}} 1&3&1 \\ 1&5&1 \\ 1&6&2 \end{array}} \right|}}{{ – 2}} = \frac{2}{{ – 2}} = – 1\) A1
\(z = \frac{{\left| {\begin{array}{*{20}{c}} 1&1&3 \\ 1&{ – 1}&5 \\ 1&1&6 \end{array}} \right|}}{{ – 2}} = \frac{{ – 6}}{{ – 2}} = 3\) A1
Note: Award M1 only if candidate attempts to determine at least one of the variables using this method.
[5 marks]
Examiners report
Question
The faces of a fair six-sided die are numbered 1, 2, 2, 4, 4, 6. Let \(X\) be the discrete random variable that models the score obtained when this die is rolled.
Complete the probability distribution table for \(X\).

Find the expected value of \(X\).
Answer/Explanation
Answer/Explanation
Markscheme
 A1A1
A1A1
Note: Award A1 for each correct row.
[2 marks]
\({\text{E}}(X) = 1 \times \frac{1}{6} + 2 \times \frac{1}{3} + 4 \times \frac{1}{3} + 6 \times \frac{1}{6}\) (M1)
\( = \frac{{19}}{6}{\text{ }}\left( { = 3\frac{1}{6}} \right)\) A1
Note: If the probabilities in (a) are not values between 0 and 1 or lead to \({\text{E}}(X) > 6\) award M1A0 to correct method using the incorrect probabilities; otherwise allow FT marks.
[2 marks]
Examiners report
[N/A]
[N/A]
Question
Two unbiased tetrahedral (four-sided) dice with faces labelled 1, 2, 3, 4 are thrown and the scores recorded. Let the random variable T be the maximum of these two scores.
The probability distribution of T is given in the following table.

Find the value of a and the value of b.
Find the expected value of T.
Answer/Explanation
Markscheme
\(a = \frac{3}{{16}}\) and \(b = \frac{5}{{16}}\) (M1)A1A1
[3 marks]
Note: Award M1 for consideration of the possible outcomes when rolling the two dice.
\({\text{E}}\left( T \right) = \frac{{1 + 6 + 15 + 28}}{{16}} = \frac{{25}}{8}\left( { = 3.125} \right)\) (M1)A1
Note: Allow follow through from part (a) even if probabilities do not add up to 1.
[2 marks]
Examiners report
[N/A]
[N/A]
Question
The continuous variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{12{x^2}(1 – x),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Determine \({\text{E}}(X)\) .
Determine the mode of X .
Answer/Explanation
Markscheme
\({\text{E}}(X) = \int_0^1 {12{x^3}(1 – x){\text{d}}x} \) M1
\( = 12\left[ {\frac{{{x^4}}}{4} – \frac{{{x^5}}}{5}} \right]_0^1\) A1
\( = \frac{3}{5}\) A1
[3 marks]
\(f'(x) = 12(2x – 3{x^2})\) A1
at the mode \(f'(x) = 12(2x – 3{x^2}) = 0\) M1
therefore the mode \( = \frac{2}{3}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
[with / without GDC]
The probability distribution of the discrete random variable X is given by the table

Find
(a) the expected value \(E(X)\) of \(X\).
(b) the mode of \(X\).
(c) the median of \(X\).
(d) the lower quartile \(Q_{1}\) and the upper quartile \(Q_{3}\).
Answer/Explanation
Ans
(a) \(2.35\) (b) mode =\(1\) (c) median = \(2\) (d) \(Q_{1}\) = \(1\) \(Q_{3}\) = \(3.5\)
Question
[without GDC]
The probability distribution of the discrete random variable X is given by the table

Find the values of \(a\) and \(b\) given that \(E(X)\) = \(2.2\)
Answer/Explanation
Ans
a = \(0.2\) b = \(0.4\)
Question
[without GDC]
The probability distribution of the discrete random variable X is given by the table.

Nikos selects a number at random.
If he selects \(1\) he earns \(10\) €. If he selects \(2\) he earns \(5\) €. If he selects \(3\) he loses \(4\) €
(a) Find the expected value of \(X\).
(b) Find the expected value of the profit for Nikos. Is the game fair?
Answer/Explanation
Ans
\(E(X)\) = \(2.2\)\) E(Profit) = \(0\), so it is fair.
Question
[without GDC]
A discrete random variable X has its probability distribution given by
\(P(X=x)=\frac{x}{6}\) where x is \(1, 2, 3\).
(a) Complete the following table showing the probability distribution for \(X\).
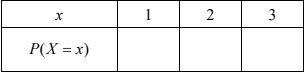
(b) Find \(E(X)\).
Answer/Explanation
Ans
(a) ![]()
(b) Find \(E(X)=7/3\)
Question
[without GDC]
Each of the following 10 words is placed on a card and put in a hat.
ONE, TWO, THREE, FOUR, FIVE, SIX, SEVEN, EIGHT, NINE, TEN
We pick a card at random. Let \(X\) be the size (number of letters) of the corresponding word.
(a) Give the probability distribution for \(X\) (i.e. the table of probabilities)
(b) Find the expected number of \(X\).
Answer/Explanation
Ans
(a) ![]()
(b) Find \(E(X) = 3.9\)
Question
[with GDC]
The probability distribution of the discrete random variable\(X\) is given by the following table.

(a) Find the value of \(p\).
(b) Calculate the expected value of \(X\).
Answer/Explanation
Ans
(a) \((0.4 + p + 0.2 + 0.07 + 0.02 = 1), \Rightarrow p = 0.31\)
(b) \(E(X) = 1(0.4) + 2(0.31) + 3(0.2) + 4(0.07) + 5(0.02) = 2\)
Question
[without GDC]
A discrete random variable X has a probability distribution as shown in the table below.

(a) Find the value of \(a + b\).
(b) Given that \(E(X) =1.5\), find the value of \(a\) and of \(b\).
Answer/Explanation
Ans
(a) \(0.1 + a + 0.3 + b = 1 \Rightarrow a + b = 0.6\)
(b) \(0\times 0.1+1\times a+2\times 0.3+3\times b\)
\(0 + a + 0.6 + 3b = 1.5\)
\(a + 3b = 0.9\)
Solving simultaneously gives
\(a = 0.45\) \(b = 0.15\)
Question
[with GDC]
The following table shows the probability distribution of a discrete random variable \(X\).

(a) Find the value of \(k\).
(b) Find the expected value of \(X\).
Answer/Explanation
Ans
(a) \(10k^{2}+3k+0.6=1\Rightarrow 10k^{2}+3k+0.4=0\Leftrightarrow k=0.1\) (by GDC)
(b) \(E(X)=-1\times 0.2+2\times 0.4+3\times 0.3=1.5\)
Question
[without GDC]
A discrete random variable \(X\) has its probability distribution given by
\(P(X = x) = k(x + 1)\), where \(x\) is \(0, 1, 2, 3, 4\).
(a) Complete the following table showing the probability distribution for \(X\) (in terms of \(k\))

(b) Show that \(k=\frac{1}{15}\)
(c) Find \(E(X)\).
Answer/Explanation
Ans
(a) ![]()
(b) \(k\times 1+k\times 2+k\times 3+k\times 4+k\times 5=15k=1\Leftrightarrow k=\frac{1}{15}\)
(c) \(E(X)=0\times \frac{1}{15}+1\times \frac{2}{15}+2\times \frac{3}{15}+3\times \frac{4}{15}+4\times \frac{5}{15}=\frac{40}{15}=\frac{8}{3}\)
Question
[without GDC]
Three students, Kim, Ching Li and Jonathan each have a pack of cards, from which they select a card at random. Each card has \(a 0, 3, 4\), or \(9\) printed on it.
(a) Kim states that the probability distribution for her pack of cards is as follows.

Explain why Kim is incorrect.
(b) Ching Li correctly states that the probability distribution for her pack of cards is as follows.

Find the value of \(k\).
(c) Jonathan correctly states that the probability distribution for his pack of cards is given by \(P(X=x)=\frac{x+1} {20}\). One card is drawn at random from his pack. Calculate the probability that the number on the card drawn
(i) is \(0\). (ii) is greater than \(0\).
Answer/Explanation
Ans
(a) Sum = \(1.3\) which is greater than \(1\)
(b) 3k + 0.7 = 1 \Rightarrow k = 0.1
(c) (i) \(P(X=0)=\frac{0+1}{20}=\frac{1}{20}\)
(ii) \(P(X>0)=1-P(X=0)=\frac{19}{20} \left ( or \frac{4}{20}+\frac{5}{20}+\frac{10}{20} \right )=\frac{19}{20}\)
Notice: in fact, the probability distribution is
![]()
Question
[with GDC]
A fair coin is tossed eight times.
(a) Calculate the probability of obtaining

(b) Find the expected number of heads and the variance of the number of heads

Answer/Explanation
Ans
(a) 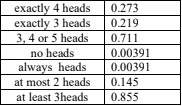
(b) ![]()