6. [Maximum mark: 6]
A continuous random variable X has the probability density function \(f_{n}\) given by
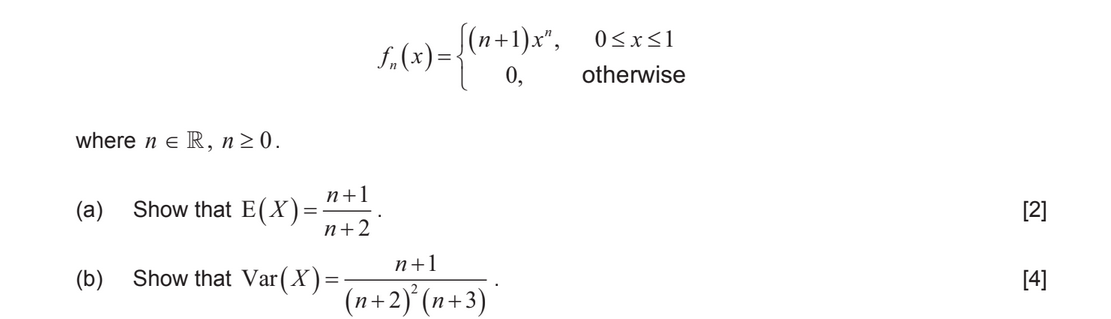
▶️Answer/Explanation


Question
A discrete random variable X has a probability distribution given in the following table.

(a) \({\text{E}}(X) = 2.61\), determine the value of p and of q.
(b) Calculate \({\text{Var}}(X)\) to three significant figures.
▶️Answer/Explanation
Markscheme
(a) \(p + q = 0.44\) A1
\(2.5p + 3.5q = 1.25\) (M1)A1
\(p = 0.29,{\text{ }}q = 0.15\) A1
(b) use of \({\text{Var}}(X) = {\text{E}}({X^2}) – {\text{E}}{(X)^2}\) (M1)
\({\text{Var}}(X) = 2.10\) A1
[6 marks]
Examiners report
An easy question, well answered by most candidates. For the others it was disappointing that many did not use the fact that the probabilities add to unity.
Question
Tim throws two identical fair dice simultaneously. Each die has six faces: two faces numbered 1, two faces numbered 2 and two faces numbered 3. His score is the sum of the two numbers shown on the dice.
(a) (i) Calculate the probability that Tim obtains a score of 6.
(ii) Calculate the probability that Tim obtains a score of at least 3.
Tim plays a game with his friend Bill, who also has two dice numbered in the same way. Bill’s score is the sum of the two numbers shown on his dice.
(b) (i) Calculate the probability that Tim and Bill both obtain a score of 6.
(ii) Calculate the probability that Tim and Bill obtain the same score.
(c) Let X denote the largest number shown on the four dice.
(i) Show that \({\text{P}}(X \leqslant 2) = \frac{{16}}{{81}}\).
(ii) Copy and complete the following probability distribution table.
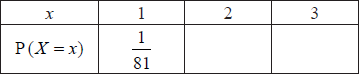
(iii) Calculate \({\text{E}}(X)\) and \({\text{E}}({X^2})\) and hence find \({\text{Var}}(X)\).
(d) Given that X = 3, find the probability that the sum of the numbers shown on the four dice is 8.
▶️Answer/Explanation
Markscheme
(a) let T be Tim’s score
(i) \({\text{P}}(T = 6) = \frac{{11}}{9}{\text{ }}( = 0.111{\text{ 3 sf)}}\) A1
(ii) \({\text{P}}(T \geqslant 3) = 1 – {\text{P}}(T \leqslant 2) = 1 – \frac{1}{9} = \frac{8}{9}{\text{ }}( = 0.889{\text{ 3 sf)}}\) (M1)A1
[3 marks]
(b) let B be Bill’s score
(i) \({\text{P}}(T = 6{\text{ and }}B = 6) = \frac{1}{9} \times \frac{1}{9} = \frac{1}{{81}}{\text{ }}( = 0.012{\text{ 3 sf)}}\) (M1)A1
(ii) \({\text{P}}(B = T) = {\text{P}}(2){\text{P}}(2) + {\text{P}}(3){\text{P}}(3) + \ldots + {\text{P}}(6){\text{P}}(6)\)
\( = \frac{1}{9} \times \frac{1}{9} + \frac{2}{9} \times \frac{2}{9} + \frac{3}{9} \times \frac{3}{9} + \frac{2}{9} \times \frac{2}{9} + \frac{1}{9} \times \frac{1}{9}\) M1
\( = \frac{{19}}{{81}}{\text{ }}( = 0.235{\text{ 3 sf)}}\) A1
[4 marks]
(c) (i) EITHER
\({\text{P}}(X \leqslant 2) = \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} \times \frac{2}{3}\) M1A1
because \({\text{P}}(X \leqslant 2) = {\text{P}}\left( {(a,{\text{ }}b,{\text{ }}c,{\text{ }}d)|a,{\text{ }}b,{\text{ }}c,{\text{ }}d = 1,{\text{ }}2} \right)\) R1
or equivalent
\({\text{P}}(X \leqslant 2) = \frac{{16}}{{81}}\) AG
OR
there are sixteen possible permutations which are
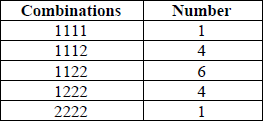 M1A1
M1A1
Note: This information may be presented in a variety of forms.
\({\text{P}}(X \leqslant 2) = \frac{{1 + 4 + 6 + 4 + 1}}{{81}}\) A1
\( = \frac{{16}}{{81}}\) AG
(ii) 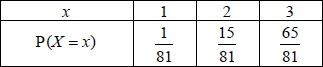 A1A1
A1A1
(iii) \({\text{E}}(X) = \sum\limits_{x = 1}^3 {x{\text{P}}(X = x)} \) (M1)
\( = \frac{1}{{81}} + \frac{{30}}{{81}} + \frac{{195}}{{81}}\)
\( = \frac{{226}}{{81}}\,\,\,\,\,\)(2.79 to 3 sf) A1
\({\text{E}}({X^2}) = \sum\limits_{x = 1}^3 {{x^2}{\text{P}}(X = x)} \)
\( = \frac{1}{{81}} + \frac{{60}}{{81}} + \frac{{585}}{{81}}\)
\( = \frac{{646}}{{81}}\,\,\,\,\,\)(7.98 to 3 sf) A1
\({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) (M1)
\( = 0.191\) (3 sf) A1
Note: Award M1A0 for answers obtained using rounded values \(\left( {e.g.{\text{ Var}}(X) = 0.196} \right)\).
[10 marks]
(d)
\({\text{P}}\left( {{\text{total is }}8 \cap (X = 3)} \right) = \frac{{18}}{{81}}\) M1A1
since \({\text{P}}(X = 3) = \frac{{65}}{{81}}\)
\({\text{P}}\left( {{\text{total is }}8|(X = 3)} \right) = \frac{{{\text{P}}\left( {({\text{total is 8)}} \cap (X = 3)} \right)}}{{{\text{P}}(X = 3)}}\) M1
\( = \frac{{18}}{{65}}{\text{ }}( = 0.277)\) A1
[4 marks]
Total [21 marks]
Examiners report
Most candidates with a reasonable understanding of probability managed to answer well parts (a), (b) and some of part (c). However some candidates did not realize that different scores were not equally likely which lead to incorrect answers in several parts. Surprisingly, many candidates completed the table in part c) ii) with values that did not add up to 1. Very few candidates answered part (d) well. The enumeration of possible cases was sometimes attempted but with little success.
Question
The probability density function of the continuous random variable X is given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k{2^{\frac{1}{x}}},}&{1 \leqslant x \leqslant 2} \\
{0,}&{{\text{otherwise}}}
\end{array}} \right.\]
where k is a constant. Find the expected value of X .
▶️Answer/Explanation
Markscheme
\(k\int_1^2 {{2^{\frac{1}{x}}}{\text{d}}x = 1 \Rightarrow k = \frac{1}{{\int_1^2 {{2^{\frac{1}{x}}}{\text{d}}x} }}{\text{ }}( = 0.61556…)} \) (M1)(A1)
\({\text{E}}(X) = k\int_1^2 {x{2^{\frac{1}{x}}}{\text{d}}x = 2.39….k{\text{ or 1.47}}} \) M1A1
Note: Condone missing dx in any part of the question.
[4 marks]
Examiners report
This question was well attempted by most candidates. However many were not alert for the necessity of using GDC to calculate the definite integrals and wasted time trying to obtain these values using standard calculus methods without success.
Question
The probability density function of a continuous random variable X is given by
\(f(x) = \frac{1}{{1 + {x^4}}}\), \(0\) \(”\) \(x\) \(”\) \(a\) .
a.Find the value of a .[3]
b.Find the mean of X .[2]
▶️Answer/Explanation
Markscheme
\(\int_0^a {\frac{1}{{1 + {x^4}}}{\text{d}}x = 1} \) M2
a = 1.40 A1
[3 marks]
\({\text{E}}(X) = \int_0^a {\frac{x}{{1 + {x^4}}}{\text{d}}x} \) M1
\(\left( { = \frac{1}{2}\arctan ({a^2})} \right)\)
= 0.548 A1
[2 marks]
Question
a.The number of cats visiting Helena’s garden each week follows a Poisson distribution with mean \(\lambda = 0.6\).
Find the probability that
(i) in a particular week no cats will visit Helena’s garden;
(ii) in a particular week at least three cats will visit Helena’s garden;
(iii) over a four-week period no more than five cats in total will visit Helena’s garden;
(iv) over a twelve-week period there will be exactly four weeks in which at least one cat will visit Helena’s garden.[9]
\(f(x) = k\ln x\) \(1 \leqslant x \leqslant 3\)
\(f(x) = 0\) otherwise
(i) Find the value of \(k\) to six decimal places.
(ii) Find the value of \({\text{E}}(X)\).
(iii) State the mode of \(X\).
(iv) Find the median of \(X\).[9]
▶️Answer/Explanation
Markscheme
(i) \(X \sim {\text{Po(0.6)}}\)
\({\text{P}}(X = 0) = 0.549{\text{ }}\left( { = {{\text{e}}^{ – 0.6}}} \right)\) A1
(ii) \({\text{P}}(X \geqslant 3) = 1 – {\text{P}}(X \leqslant 2)\) (M1)(A1)
\( = 1 – \left( {{{\text{e}}^{ – 0.6}} + {{\text{e}}^{ – 0.6}} \times 0.6 + {{\text{e}}^{ – 0.6}} \times \frac{{{{0.6}^2}}}{2}} \right)\)
\( = 0.0231\) A1
(iii) \(Y \sim {\text{Po(2.4)}}\) (M1)
\({\text{P}}(Y \leqslant 5) = 0.964\) A1
(iv) \(Z \sim {\text{B(12, 0.451}} \ldots )\) (M1)(A1)
Note: Award M1 for recognising binomial and A1 for using correct parameters.
\({\text{P}}(Z = 4) = 0.169\) A1
[9 marks]
(i) \(k\int_1^3 {\ln x{\text{d}}x = 1} \) (M1)
\((k \times 1.2958 \ldots = 1)\)
\(k = 0.771702\) A1
(ii) \({\text{E}}(X) = \int_1^3 {kx\ln x{\text{d}}x} \) (A1)
attempting to evaluate their integral (M1)
\( = 2.27\) A1
(iii) \(x = 3\) A1
(iv) \(\int_1^m {k\ln x{\text{d}}x = 0.5} \) (M1)
\(k[x\ln x – x]_1^m = 0.5\)
attempting to solve for m (M1)
\(m = 2.34\) A1
[9 marks]