Question
The continuous random variable X has probability density function
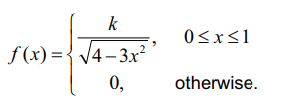
(a) Find the value of k .
(b) Find E(X) .
Answer/Explanation
Ans:
(a) attempt to integrate \(\frac{k}{\sqrt{4-3x^{2}}}\)
\(= k \left \lfloor \frac{1}{\sqrt{3}}arcsin\left ( \frac{\sqrt{3}}{2}x \right ) \right \rfloor\)
Note: Award (M1)A0 for arcsin \(\left ( \frac{\sqrt{3}}{2}x \right )\)
Condone absence of k up to this stage.
equating their integrand to 1
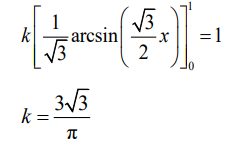
(b) \(E(X) = \frac{3\sqrt{3}}{\pi }\int_{0}^{1}\frac{x}{\sqrt{4-3x^{2}}}dx\)
Note: Condone absence of limits if seen at a later stage.
EITHER
attempt to integrate by inspection
\( = \frac{3\sqrt{3}}{\pi }\times -\frac{1}{6}\int -6x\left ( 4-3x^{2} \right )^{-\frac{1}{2}}dx\)
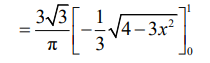
Note: Condone the use of k up to this stage.
OR
for example, \(u = 4-3c^{2} \Rightarrow \frac{du}{dx}= -6x\)
Note: Other substitutions may be used. For example, u = −3x2.
\(= – \frac{\sqrt{3}}{2\pi } \int_{4}^{1}u^{-\frac{1}{2}} du\)
Note: Condone absence of limits up to this stage.

Question
A continuous random variable X has the probability density function
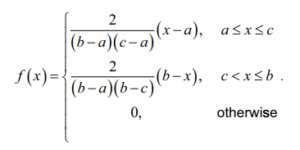
The following diagram shows the graph of y = f (x) for a ≤ x ≤ b .
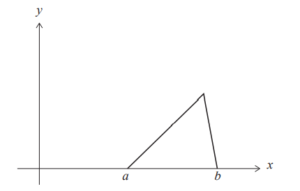
Given that \(c\geq \frac{a+b}{2},\) find an expression for the median of X in terms of a , b and c .
Answer/Explanation
Ans:
let m be the median
EITHER
attempts to find the area of the required triangle
base is ( m – a )
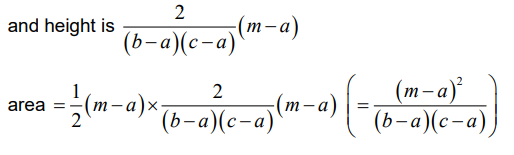
OR
attempts to integrate the correct function
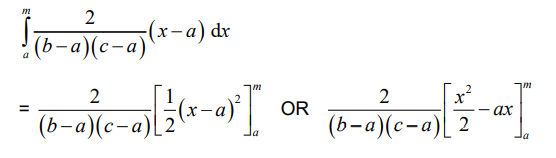
Note: Award A1 for correct integration and A1 for correct limits.
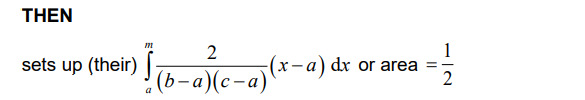
Note: Award M0A0A0M1A0A0 if candidates conclude that m > c and set up their area or sum of integrals \(=\frac{1}{2}.\)
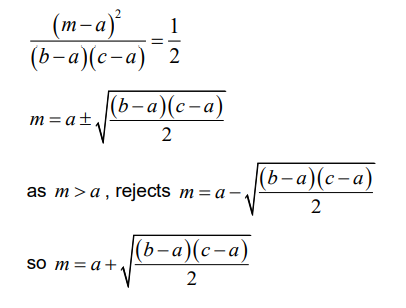
Question
The continuous random variable X has cumulative distribution function F , where F(a) = 0 and F(b) = 1 .
Using integration by parts, show that E( X ) = b – a∫b F (x)dx . [4]
Let F (x) =
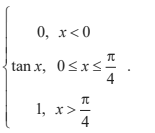
Using the result from part (a), determine E(X ) . Give your answer correct to three significant figures. [2]
Determine the median of X , giving your answer correct to three significant figures. [2]
Answer/Explanation
Ans:
(a)
let X have probability density function f. Then
E (X) = \(\int_{a}^{b} xf(x) dx (= \int_{a}^{b} x \frac{df(x)}{dx})\)
=\([xf(x)]_{b}^{a} – \int_{a}^{b} F (x)dx\)
= \(b\times 1- a \times 0 – \int_{a}^{b} F(x)dx\)
= \(b – \int_{a}^{b} F (x)dx\)
(b) E (X) = \(\frac{\pi}{4}- \int_{a}^{b} tan xdx\) = 0.439
(c) the median m satisfies F ( m) = tan 0.5 = m = 0.464
Question
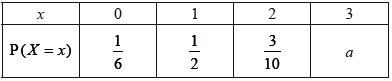
A discrete random variable, X, has the following probability distribution:
| x | 0 | 1 | 2 | 3 |
| P(X = x) | 0.41 | k – 0.28 | 0.46 | 0.29 – 2k2 |
(a) Show that 2k2 – k + 0.12 = 0.
(b) Find the value of k , giving a reason for your answer.
(c) Hence, find E(X).
Answer/Explanation
Ans:
(a) 0.41 + k – 0.28 + 0.46 + 0.29 – 2k2 = 1 OR k – 2k2 + 0.01 = 0.13 (or equivalent)
2k2 – k + 0.12 = 0
(b) one of 0.2 OR 0.3
k = 0.3
reasoning to reject k = 0.2 eg P(1) = k – 0.28 0 ≥ 0 therefore k ≠ 0.2
(c) attempting to use the expected value formula
E(X) = 0 × 0.41 + 1 × (0.3 – 0.28) + 2 × 0.46 + 3 ×(0.29 – 2 × 0.32)
= 1.27
Note: Award M1A0 if additional values are given.
Question
A random variable has a probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{kx(2 – x),}&{0 \leqslant x \leqslant 2} \\
{0,}&{{\text{elsewhere}}{\text{.}}}
\end{array}} \right.\]
(a) Show that \(k = \frac{3}{4}\) .
(b) Find \({\text{E}}(X)\) .
Answer/Explanation
Markscheme
(a) \(\int_0^2 {kx(2 – x){\text{d}}x = 1} \) M1A1
Note: Award M1 for LHS and A1 for setting = 1 at any stage.
\(\left[ {\frac{{2k}}{2}{x^2} – \frac{k}{3}{x^3}} \right]_0^2 = 1\) A1
\(k\left( {4 – \frac{8}{3}} \right) = 1\) A1
\(k = \frac{3}{4}\) AG
(b) \({\text{E}}(X) = \frac{3}{4}\int_0^2 {{x^2}(2 – x){\text{d}}x} \) (M1)
= 1 A1
Note: Accept answers that indicate use of symmetry.
[6 marks]
Examiners report
The integration was particularly well done in this question. A number of students treated the distribution as discrete. On the whole a) was done well once the distribution was recognized although there was a certain amount of fudging to achieve the result. A significant number of students did not initially set the integral equal to 1. Very few noted the symmetry of the distribution in b).
Question
A continuous random variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{0,}&{x < 0} \\
{a{{\text{e}}^{ – ax}},}&{x \geqslant 0.}
\end{array}} \right.\]
It is known that \({\text{P}}(X < 1) = 1 – \frac{1}{{\sqrt 2 }}\).
(a) Show that \(a = \frac{1}{2}\ln 2\).
(b) Find the median of X.
(c) Calculate the probability that X < 3 given that X >1.
Answer/Explanation
Markscheme
(a) \(\int_0^1 {a{{\text{e}}^{ – ax}}} {\text{d}}x = 1 – \frac{1}{{\sqrt 2 }}\) M1A1
\(\left[ { – {{\text{e}}^{ – ax}}} \right]_0^1 = 1 – \frac{1}{{\sqrt 2 }}\) M1A1
\( – {{\text{e}}^{ – a}} + 1 = 1 – \frac{1}{{\sqrt 2 }}\) A1
Note: Accept \({{\text{e}}^0}\) instead of 1.
\({{\text{e}}^{ – a}} = \frac{1}{{\sqrt 2 }}\)
\({{\text{e}}^a} = \sqrt 2 \)
\(a = \ln {2^{\frac{1}{2}}}\,\,\,\,\,\left( {{\text{accept }} – a = \ln {2^{ – \frac{1}{2}}}} \right)\) A1
\(a = \frac{1}{2}\ln 2\) AG
[6 marks]
(b) \(\int_0^M {a{{\text{e}}^{ – ax}}{\text{d}}x = \frac{1}{2}} \) M1A1
\(\left[ { – {{\text{e}}^{ – ax}}} \right]_0^M = \frac{1}{2}\) A1
\( – {{\text{e}}^{ – Ma}} + 1 = \frac{1}{2}\)
\({{\text{e}}^{ – Ma}} = \frac{1}{2}\) A1
\(Ma = \ln 2\)
\(M = \frac{{\ln 2}}{a} = 2\) A1
[5 marks]
(c) \({\text{P}}(1 < X < 3) = \int_1^3 {a{{\text{e}}^{ – ax}}{\text{d}}x} \) M1A1
\( = – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}\) A1
\({\text{P}}(X < 3|X > 1) = \frac{{{\text{P}}(1 < X < 3)}}{{{\text{P}}(X > 1)}}\) M1A1
\( = \frac{{ – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}}}{{1 – {\text{P}}(X < 1)}}\) A1
\( = \frac{{ – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}}}{{\frac{1}{{\sqrt 2 }}}}\) A1
\( = \sqrt 2 ( – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}})\)
\( = \sqrt 2 \left( { – {2^{ – \frac{3}{2}}} + {2^{ – \frac{1}{2}}}} \right)\) A1
\( = \frac{1}{2}\) A1
Note: Award full marks for \({\text{P}}(X < 3/X > 1) = {\text{P}}(X < 2) = \frac{1}{2}\) or quoting properties of exponential distribution.
[9 marks]
Total [20 marks]
Examiners report
Many candidates did not attempt this question and many others were clearly not familiar with this topic. On the other hand, most of the candidates who were familiar with continuous random variables and knew how to start the questions were successful and scored well in parts (a) and (b). The most common errors were in the integral of \({e^{ – at}}\), having the limits from \( – \infty \) to 1, confusion over powers and signs (‘-’ sometimes just disappeared). Understanding of conditional probability was poor and marks were low in part (c). A small number of candidates from a small number of schools coped very competently with the algebra throughout the question.
Question
A continuous random variable X has the probability density function f given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{c(x – {x^2}),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
(a) Determine c.
(b) Find \({\text{E}}(X)\).
Answer/Explanation
Markscheme
(a) the total area under the graph of the pdf is unity (A1)
area \( = c\int_0^1 {x – {x^2}{\text{d}}x} \)
\( = c\left[ {\frac{1}{2}{x^2} – \frac{1}{3}{x^3}} \right]_0^1\) A1
\( = \frac{c}{6}\)
\( \Rightarrow c = 6\) A1
(b) \({\text{E}}(X) = 6\int_0^1 {{x^2} – {x^3}{\text{d}}x} \) (M1)
\( = 6\left( {\frac{1}{3} – \frac{1}{4}} \right) = \frac{1}{2}\) A1
Note: Allow an answer obtained by a symmetry argument.
[5 marks]
Examiners report
Most candidates made a meaningful attempt at this question with many gaining the correct answers. One or two candidates did not attempt this question at all.
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The probability density function of the random variable X is defined as
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{\sin x,}&{0 \leqslant x \leqslant \frac{\pi }{2}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find \({\text{E}}(X)\).
Answer/Explanation
Markscheme
\(\int_0^{\frac{\pi }{2}} {x\sin x{\text{d}}x} \) M1
\( = [ – x\cos x]_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {\cos x{\text{d}}x} \) M1(A1)
Note: Condone the absence of limits or wrong limits to this point.
\( = [ – x\cos x + \sin x]_0^{\frac{\pi }{2}}\) A1
\( = 1\) A1
[5 marks]
Examiners report
It was pleasing to note how many candidates recognised the expression that needed to be integrated and successfully used integration by parts to reach the correct answer.
Question
The discrete random variable X has probability distribution:
(a) Find the value of a.
(b) Find \({\text{E}}(X)\).
(c) Find \({\text{Var}}(X)\).
Answer/Explanation
Markscheme
(a) \(\frac{1}{6} + \frac{1}{2} + \frac{3}{{10}} + a = 1 \Rightarrow a = \frac{1}{{30}}\) A1
(b) \({\text{E}}(X) = \frac{1}{2} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{{30}}\) M1
\(= \frac{6}{5}\) A1
Note: Do not award FT marks if a is outside [0, 1].
[2 marks]
(c) \({\text{E}}({X^2}) = \frac{1}{2} + {2^2} \times \frac{3}{{10}} + {3^2} \times \frac{1}{{30}} = 2\) (A1)
attempt to apply \({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) M1
\(\left( { = 2 – \frac{{36}}{{25}}} \right) = \frac{{14}}{{25}}\) A1
[3 marks]
Total [6 marks]
Examiners report
This was very well answered and many fully correct solutions were seen. A small number of candidates made arithmetic mistakes in part a) and thus lost one or two accuracy marks. A few also seemed unaware of the formula \({\text{Var}}(X) = {\text{E}}({X^2}) – {\text{E}}{(X)^2}\) and resorted to seeking an alternative, sometimes even attempting to apply a clearly incorrect \({\text{Var}}(X) = \sum {{{({x_i} – \mu )}^2}} \).
Question
A continuous random variable \(T\) has probability density function \(f\) defined by
\[f(t) = \left\{ {\begin{array}{*{20}{c}} {\left| {2 – t} \right|,}&{1 \le t \le 3} \\ {0,}&{{\text{otherwise.}}} \end{array}} \right.\]
Sketch the graph of \(y = f(t)\).
Find the interquartile range of \(T\).
Answer/Explanation
Markscheme
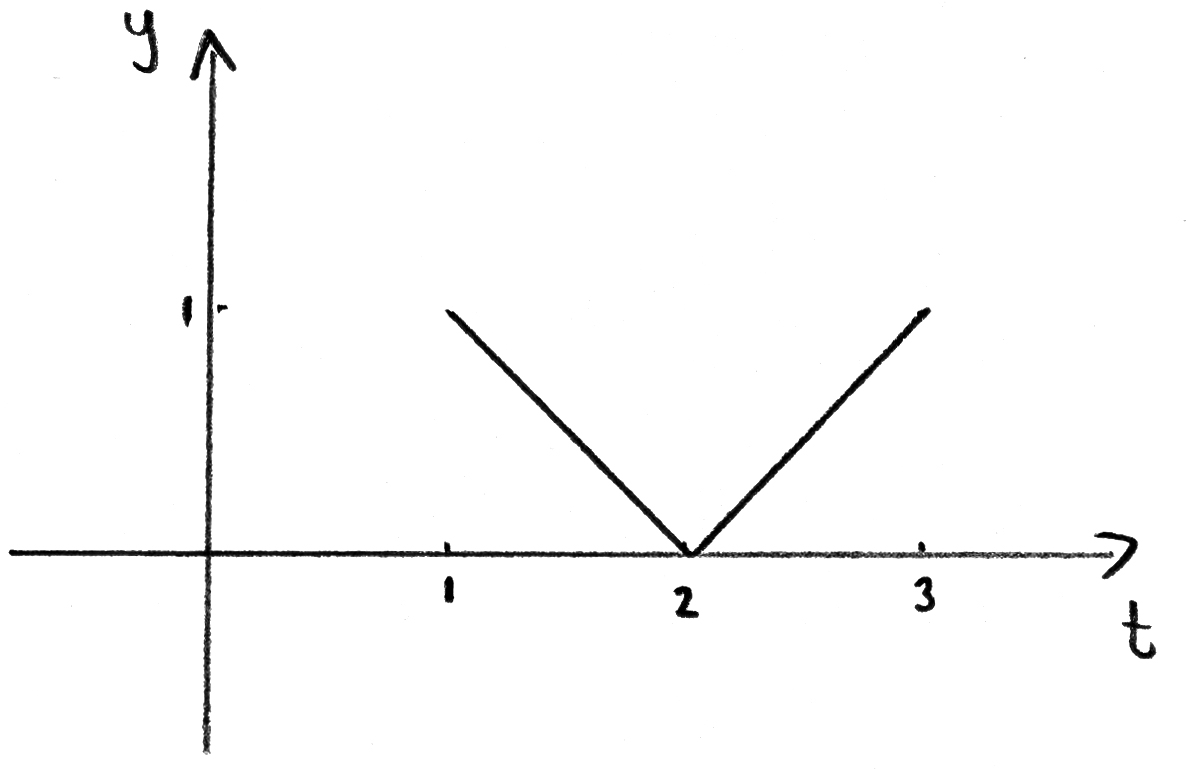
\(\left| {2 – t} \right|\) correct for \(\left[ {1,{\text{ }}2} \right]\) A1
\(\left| {2 – t} \right|\) correct for \(\left[ {2,{\text{ }}3} \right]\) A1
EITHER
let \({q_1}\) be the lower quartile and let \({q_3}\) be the upper quartile
let \(d = 2 – {q_1}{\text{ }}( = {q_3} – 2)\) and so \({\text{IQR}} = 2d\) by symmetry
use of area formulae to obtain \(\frac{1}{2}{d^2} = \frac{1}{4}\)
(or equivalent) M1A1
\(d = \frac{1}{{\sqrt 2 }}\) or the value of at least one \(q\). A1
OR
let \({q_1}\) be the lower quartile
consider \(\int_1^{{q_1}} {(2 – t){\text{d}}t = \frac{1}{4}} \) M1A1
obtain \({q_1} = 2 – \frac{1}{{\sqrt 2 }}\) A1
THEN
\({\text{IQR}} = \sqrt 2 \) A1
Note: Only accept this final answer for the A1.
[4 marks]
Total [6 marks]
Examiners report
The sketched graphs were mostly acceptable, but sometimes scrappy.
Most candidates had some idea about the upper and lower quartiles, but some were rather vague about how to calculate them for this probability density function. Even those who integrated for the lower quartile often made algebraic mistakes in calculating its value.
Question
The continuous variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{12{x^2}(1 – x),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Determine \({\text{E}}(X)\) .
Determine the mode of X .
Answer/Explanation
Markscheme
\({\text{E}}(X) = \int_0^1 {12{x^3}(1 – x){\text{d}}x} \) M1
\( = 12\left[ {\frac{{{x^4}}}{4} – \frac{{{x^5}}}{5}} \right]_0^1\) A1
\( = \frac{3}{5}\) A1
[3 marks]
\(f'(x) = 12(2x – 3{x^2})\) A1
at the mode \(f'(x) = 12(2x – 3{x^2}) = 0\) M1
therefore the mode \( = \frac{2}{3}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
The continuous variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{12{x^2}(1 – x),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Determine \({\text{E}}(X)\) .
Determine the mode of X .
Answer/Explanation
Markscheme
\({\text{E}}(X) = \int_0^1 {12{x^3}(1 – x){\text{d}}x} \) M1
\( = 12\left[ {\frac{{{x^4}}}{4} – \frac{{{x^5}}}{5}} \right]_0^1\) A1
\( = \frac{3}{5}\) A1
[3 marks]
\(f'(x) = 12(2x – 3{x^2})\) A1
at the mode \(f'(x) = 12(2x – 3{x^2}) = 0\) M1
therefore the mode \( = \frac{2}{3}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
A continuous random variable X has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k\sin x,}&{0 \leqslant x \leqslant \frac{\pi }{2}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the value of k.
Find \({\text{E}}(X)\).
Find the median of X.
Answer/Explanation
Markscheme
\(k\int_0^{\frac{\pi }{2}} {\sin x{\text{d}}x = 1} \) M1
\(k[ – \cos x]_0^{\frac{\pi }{2}} = 1\)
k = 1 A1
[2 marks]
\({\text{E}}(X) = \int_0^{\frac{\pi }{2}} {x\sin x{\text{d}}x} \) M1
integration by parts M1
\([ – x\cos x]_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {\cos x{\text{d}}x} \) A1A1
= 1 A1
[5 marks]
\(\int_0^M {\sin x{\text{d}}x} = \frac{1}{2}\) M1
\([ – \cos x]_0^M = \frac{1}{2}\) A1
\(\cos M = \frac{1}{2}\)
\(M = \frac{\pi }{3}\) A1
Note: accept \(\arccos \frac{1}{2}\)
[3 marks]
Examiners report
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Question
The continuous random variable \(X\) has probability density function
\(f(x)=\frac{1}{5}\) \(0\leq x\leq a\)
which is shown in the diagram below (it is known as uniform distribution.
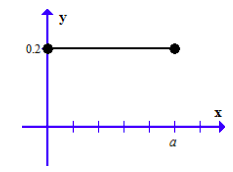
(a) Find the value of \(a\).
(b) Find \(P(X = 2)\) and \(P(X < 2)\)
(c) Find the mean of \(X\).
(d) Find \(E(X^{2})\) and hence Var\((X)\)
Answer/Explanation
Ans
(a) \(a=5\) (area under the curve is 1)
(b) \(P(X=2)=0\)
\(P(X<2)=0.4\)
(c) mean= \(E(X)=\int_{0}^{5}x\ f(x)dx=\int_{0}^{5}0.2\ xdx=\left [ 0.1x^{2} \right ]_{0}^{5}=2.5\) \((=\frac{5}{2})\)
(the midpoint of the interval \(\left [ 0,5 \right ]\))
(d) \(E(X^{2})=\int_{0}^{5}x^{2}f(x)dx=\int_{0}^{5}0.2\ x^{2}dx=\left [ \frac{0.2x^{3}}{3} \right ]_{0}^{5}=\frac{25}{3}\)
Hence, Var(X) =\(\frac{25}{3}-\left ( \frac{5}{2} \right )^{2}=\frac{25}{12}\) \((=2.08)\)
Question
[Use GDC if necessary]
The continuous random variable \(X\) has probability density function
\(f(x)=\left\{\begin{matrix}
1.5x+1 & -\frac{2}{3}\leq x\leq 0
\\1-x^{2} & 0\leq x\leq 1
\\0 & otherwise
\end{matrix}\right.\)
which is shown in the diagram below.
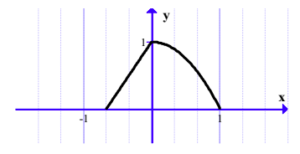
(a) Justify that \(f\) is a pdf.
(b) Find \(P(X = – 1)\) and \(P(X > 0.5)\)
(c) Find the mean of \(X\) .
(d) Find \(E(X^{2})\) and hence \(Var(X)\)
(e) Find \(E(2X+1)\)
(f) Find the mode, the median and the quartiles \(Q_{1}\) and \(Q_{3}\) of \(X\)
Answer/Explanation
Ans
(a) \(f(x)\geq 0\) and
\(\int_{-2/3}^{1}f(x)\ dx=\frac{1}{3}+\int_{0}^{1}\left ( 1-x^{2} \right )dx=1\)
(b) \(P(X=-1)=0\)
\(P(X>0.5)=\int_{0.5}^{1}(1-x^{2})dx=0.208\)
(c) mean =\(E(X)=\int_{-2/3}^{1}x\ f(x)dx=\int_{0}^{1}(1.5x^{2}+x)dx+\int_{0}^{1}(x-x^{3})dx=0.176\)
(d) \(E(X^{2})=\int_{-2/3}^{1}x^{2}\ f(x)dx=\int_{0}^{1}(1.5x^{3}+x^{2})dx+\int_{0}^{1}(x^{2}-x^{4})dx=0.158\)
\(Var(X)=0.158-0.176^{2}=0.127\)
(e) \(E(2X+1)=\int_{-2/3}^{1}(2x+1)f(x)dx=1.35\)
mode=\(0\),
median=\(0.0168\), by solving \(\int_{-2/3}^{M}f(x)dx=\frac{1}{2}\Rightarrow \int_{0}^{M}(1-x^{2})dx=\frac{1}{2}-\frac{1}{3}\)
\(Q_{1}=0.089\) by solving \(\int_{-2/3}^{Q_{1}}f(x)dx=\frac{1}{4}\Rightarrow \int_{-2/3}^{Q_{1}}(1.5x+1)dx=\frac{1}{4}\)
\(Q_{1}=0.446\) by solving \(\int_{Q_{1}}^{1}f(x)dx=\frac{1}{4}\Rightarrow \int_{Q_{1}}^{1}(1-x^{2})dx=\frac{1}{4}\)
Question
The continuous random variable X has probability density function
\(f(x)=\frac{1}{6}x(1+x^{2})\) for \(0\leq x\leq 2\),
\(f(x)=0\) otherwise.
(a) Sketch the graph of \(f\) for \(0\leq x\leq 2\).
(b) Write down the mode of \(X\).
(c) Find the mean of \(X\).
(d) Find the median of \(X\).
Answer/Explanation
Ans
(a) 
(b) Mode = \(2\)
(c) Using \(E(X)=\int_{a}^{b}x\ f(x)dx\)
Mean =\(\frac{1}{6}\int_{0}^{2}x\ f(x)dx\)
Mean=\(\frac{1}{6}\int_{0}^{2}(x^{2}+x^{4}dx)=\frac{1}{6}\left [ \frac{x^{3}}{3}+\frac{x^{5}}{5} \right ]_{0}^{2}=\frac{68}{45}(1.51)\)
(d) The median m satisfies \(\frac{1}{6}\int_{0}^{2}(x^{2}+x^{4})dx=\frac{1}{6}\int_{0}^{m}(x+x^{3})dx=\frac{1}{2}\)
\(\frac{m^{2}}{2}+\frac{m^{4}}{2}=3\Rightarrow m^{4}+2m^{2}-12=0\)
\(m^{2}=\frac{-2\pm \sqrt{4+48}}{2}=2.60555…\Rightarrow m=1.61\)
Question
Let \(f (x)\) be the probability density function for a random variable \(X\), where
\(f(x)=\left\{\begin{matrix}
kx^{2}, & for\ 0\leq x\leq 2
\\ 0, & otherwise
\end{matrix}\right.\)
(a) Show that \(k=\frac{3}{8}\)
(b) Calculate (i) \(E(X)\); (ii) the median of \(X\).
Answer/Explanation
Ans
(a) \(k\int_{0}^{2}x^{2}dx=1\Rightarrow k\left [ \frac{x^{3}}{3} \right ]_{0}^{2}=\frac{k8}{3}=1\Rightarrow k=\frac{3}{8}\)
(b) (i) \(E(X)=\frac{3}{8}\int_{0}^{2}x\ x^{2}dx\ (=\frac{3}{8}\left [ \frac{x^{4}}{4} \right ]_{0}^{2})=\frac{3}{2}\)
(ii) \(\frac{3}{8}\int_{0}^{m}x^{2}dx=\frac{1}{2}\left ( or\ \frac{3}{8}\int_{m}^{2}x^{2}dx \right )\)
\(\frac{3}{8}\left [ \frac{x^{3}}{3} \right ]_{0}^{m}=\frac{3}{8}\left ( \frac{m^{3}}{3}-0 \right )=\frac{1}{2}\)
\(\frac{m^{3}}{8}=\frac{1}{2}\Rightarrow m^{3}=4,\Rightarrow m=\sqrt[3]{4}\) (=\(1.59\) to \(3\) s.f.).
Question
A continuous random variable \(X\) has probability density function
\(f(x)=\left\{\begin{matrix}
12x^{2}(1-x), & for\ 0\leq 1,
\\0, & otherwise.
\end{matrix}\right.\)
Find the probability that X lies between the mean and the mode.
Answer/Explanation
Ans
Attempting to find the mode graphically or by using \(f'(x)=12x(2-3x)\)
Mode=\(\frac{2}{3}\)
Use of \(E(X)=\int_{0}^{1}x\ f(x)dx\Rightarrow E(X)=\frac{3}{5}\)
\(\int_{\frac{3}{5}}^{\frac{2}{3}}f(x)dx=0.117\left ( =\frac{1981}{16875} \right )\)
Question
A continuous random variable \(X\) has a probability density function given by
\(f(x)=\left\{\begin{matrix}
\frac{(x+1)^{3}}{60}, & for\ 1\leq x\leq 3,
\\0, & otherwise.
\end{matrix}\right.\)
Find
(a) \(P(1.5\leq X\leq 2.5);\) (b) \(E(X);\) (c) the median of \(X\).
Answer/Explanation
Ans
(a) \(\int_{1.5}^{2.5}\frac{(x+1)^{3}}{60}dx=0.4625(=0.463)\)
(b) \(E(X)=\int_{1}^{3}\frac{x(x+1)^{3}}{60}dx=2.31\)
(c) \(\int_{1}^{m}\frac{(x+1)}{60}dx=0.5\Rightarrow \left [ \frac{(x+1)^{4}}{240} \right ]_{1}^{m}=0.5\Rightarrow m=2.41\)
Question
A continuous random variable \(X\) has probability density function \(f\) defined by
\(f(x)=\left\{\begin{matrix}
e^{x}, & for\ 0\leq x\leq \ln 2
\\0, & otherwise
\end{matrix}\right.\)
Find the exact value of \(E( X )\)
Answer/Explanation
Ans
\(E(X)=\int_{0}^{\ln 2}xe^{x}dx\)
Attempting to use integration by parts
\(\int xe^{x}dx=xe^{x}-\int e^{x}dx\)
\(E(X)=\left [ xe^{x}- e^{x}\right ]_{0}^{\ln 2}\)
\(=2\ln 2-1=\left ( \ln 4-1, \ln \frac{4}{e} \right )\)
Question
A continuous random variable \(X\) has probability density function \(f\) given by
\(f(x)=\left\{\begin{matrix}
\frac{8}{\pi (x^{2}+4)}, & 0\leq x\leq 2
\\0, & otherwise
\end{matrix}\right.\)
(a) State the mode of \(X\).
(b) Find the exact value of \(E( X )\).
Answer/Explanation
Ans
(a) Mode=\(0\)
(b) \(E(X)=\frac{8}{\pi }\int_{0}^{2}\frac{x}{x^{2}+4}dx\)
Attempting substitution method or using \(\int \frac{f'(x)}{f(x)}dx=\ln f(x)\)
\(E(X)=\frac{4}{\pi }\ln u\ _{4}^{8}or E(X)=\frac{4}{\pi }\left [ \ln (x^{2}+4) \right ]_{0}^{2}\)
\(=\frac{4}{\pi }(\ln 8-\ln 4)\left ( =\frac{4}{\pi }\ln \frac{8}{4},=\frac{4}{\pi }\ln 2 \right )\)
Extra questions
(c) Justify that \(f\) is a \(pdf\)
(d) Find \(E(X^{2})\)
Ans
(c) \(f(x)\geq 0and \frac{8}{\pi}\int_{0}^{2}\frac{1}{x^{2}+4}dx=\frac{8}{\pi}\left [ \frac{1}{2} arctan\ \frac{x}{2}\right ]_{0}^{2}=1\)
(d) \(E(X^{2})=\frac{8}{\pi}\int_{0}^{2}\frac{x^{2}}{x^{2}+4}dx=\frac{8}{\pi}\left [ \frac{1}{2} arctan \frac{x}{2}\right ]_{0}^{2}=\frac{8}{\pi}\int_{0}^{2}\frac{x^{2}}{x^{2}+4}dx=\frac{16}{\pi }-4(=1.093)\)
Question
The probability density function \(f (x)\) of the continuous random variable \(X\) is defined on the interval \([0,a]\) by
\(f(x)=\left\{\begin{matrix}
\frac{1}{8}x & for\ 0\leq x\leq 3,
\\\frac{27}{8x^{2}}& for 3< x\leq a.
\end{matrix}\right.\)
Find the value of \(a\).
Answer/Explanation
Ans
Using \(\int_{0}^{a}f(x)dx=1\)
\(\int_{0}^{3}\frac{1}{8}x\ dx=\frac{9}{16}(=0.5625)\)
\(\int_{3}^{a}\frac{27}{8x^{2}}dx=\frac{27}{8}(-\frac{1}{a}+\frac{1}{3})=-\frac{27}{8a}+\frac{9}{8}\)
\(-\frac{27}{8a}+\frac{9}{8}=\frac{7}{16}\)
\(\Rightarrow a=\frac{54}{11}(=4.91)\)
Extra question
Find the mean and the median of \(X\)
Ans
mean=\(2.79\) and median=\(\sqrt{8}=2.83\)
Question
The random variable \(T\) has the probability density function
\(f(t)=\frac{\pi}{4}\cos \left ( \frac{\pi t}{2} \right ),-1\leq t\leq 1\).
Find
(a) \(P(T = 0)\);
(b) the interquartile range.
Answer/Explanation
Ans
(a) Any consideration of \(\int_{0}^{0}f(x)dx \) It is 0.
(b) METHOD 1
Let the upper and lower quartiles be \(a\) and \(-a\)
\(\frac{\pi }{4}\int_{a}^{1}\cos \frac{\pi t}{2}dt=0.25\Rightarrow \left [ \frac{\pi }{4}\times \frac{2}{\pi }\sin \frac{\pi t}{2} \right ]_{a}^{1}=0.25\)
\(\Rightarrow \left [ \frac{1}{2}\sin \frac{\pi t}{2} \right ]_{a}^{1}=0.25\Rightarrow \left [ \frac{1}{2}-\frac{1}{2}\sin \frac{\pi a}{2} \right ]=0.25\)
\(\Rightarrow \frac{1}{2}\sin \frac{\pi a}{2}=\frac{1}{4}\Rightarrow \sin \frac{\pi a}{2}=\frac{1}{2}\ \frac{\pi a}{2}=\frac{\pi }{6}\Rightarrow a=\frac{1}{3}\)
Since the function is symmetrical about \(t\)=0,
interquartile range is \(\frac{1}{3}-\left ( -\frac{1}{3} \right )=\frac{2}{3}\)
METHOD 2
\(\frac{\pi }{4}\int_{-a}^{a}\cos \frac{\pi t}{2}dt=0.5=\frac{\pi }{2}\int_{0}^{1}\cos \frac{\pi t}{2}dt\)
\(\Rightarrow \left [ \sin \frac{a\pi }{2} \right ]=0.5\Rightarrow \frac{a\pi }{2}=\frac{\pi }{6}\Rightarrow a=\frac{1}{3}\)
The interquartile range is \(\frac{2}{3}\)
Extra question
Find the mean and the median of \(X\)
Ans
mean = \(\frac{\pi }{4}\int_{-1}^{1}x\cos \frac{\pi x}{2}dx=0\)
or since the function is symmetric about mean = \(0\)
median = \(0\) (again by symmetry)
Question
The time, \(T\) minutes, required by candidates to answer a question in a mathematics examination has probability
density function
\(f(t)=\left\{\begin{matrix}
\frac{1}{72}(12t-t^{2}-20), & for\ 4\leq t\leq 10
\\0, & otherwise
\end{matrix}\right.\)
(a) Find (i) \(μ\), the expected value of \(T\) ; (ii) \(\sigma ^{2}\), the variance of \(T\).
(b) A candidate is chosen at random. Find the probability that the time taken by this candidate to answer the question
lies in the interval \([μ – σ , μ]\).
Answer/Explanation
Ans
(a) (i) \(\mu =\frac{1}{72}\int_{4}^{10}t(12t-t^{2}-20)dt\) (using \(\mu =\int t\ f(t)dt)\)
=\(6.5\)
(ii) \(E(T^{2})=\frac{1}{72}\int_{4}^{10}t^{2}(12t-t^{2}-20)dt\) (using \(\int t^{2}\ f(t)dt)\)
\(44.4\)
\(\sigma ^{2}=E(T^{2})-\mu ^{2}\)
=\(44.4-6.5^{2}\)
=\(2.15\)
(b) \(\left [ \mu -\sigma,\mu \right ]=\left [ 6.5-\sqrt{2.15},6.5 \right ] (=\left [ 5.03…,6.5 \right ])\)
required probability \(\frac{1}{72}\int_{5.03..}^{6.5}(12t-t^{2}-20)dt\)
=\(0.321\) (accept \(0.322\))
Question
The continuous random variable \(Χ\) has probability density function
\(f(x)=\left\{\begin{matrix}
\frac{x}{1+x^{2}}, & for\ 0\leq x\leq k
\\0, & otherwise
\end{matrix}\right.\)
(a) Find the exact value of k.
(b) Find the mode of \(X\).
(c) Calculate \(P(1 ≤ X ≤ 2)\).
Answer/Explanation
Ans
(a) \(\int_{0}^{k}\frac{x}{1+x^{2}}dx=1\)
\(\left [ \frac{1}{2}\ln (1+x^{2}) \right ]_{0}^{k}=1\)
\(\frac{1}{2}\ln (1+k^{2})=1\)
\(\ln (1+k^{2})=2\)
\(1+k^{2}=e^{2}\)
\(k^{2}=e^{2}-1\)
\(k=\sqrt{e^{2}-1}\)
(b) At the mode, f(x) is a maximum
The mode is \(1\)
(c) \(P(1\leq X\leq 2)=\int_{1}^{2}\frac{x}{1+x^{2}}dx=0.458 \left ( =\frac{1}{2}\ln \left ( \frac{5}{2} \right ) \right )\)
Question
A continuous random variable \(Χ\) has probability density function defined by
\(f(x)=\left\{\begin{matrix}
\frac{c}{4+x^{2}}, & for\ -\frac{2}{\sqrt{3}}\leq x\leq 2\sqrt{3}
\\0, & otherwise
\end{matrix}\right.\)
(a) Find the exact value of the constant \(c\) in terms of \(π\).
(b) Sketch the graph of \(f (x)\) and hence state the mode of the distribution.
(c) Find the exact value of \(Ε( Χ )\).
Answer/Explanation
Ans
(a) \(\int_{-\frac{2}{\sqrt{3}}}^{2\sqrt{3}}\frac{c}{4+x^{2}}dx=1\)
\(\Rightarrow \left [ \frac{c}{2}\tan ^{-1}\frac{x}{2} \right ]_{-\frac{2}{\sqrt{3}}}^{2\sqrt{3}}=1\)
\(\Rightarrow \frac{c}{2}\times \frac{\pi }{3}+\frac{c}{2}\times \frac{\pi }{6}=1 \Rightarrow \frac{3c\pi }{12}=1\Rightarrow c=\frac{4}{\pi }\)
(b) 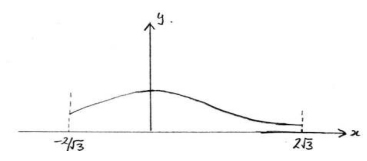
The mode is \(0\).
(c) \(E(X)=\frac{4}{\pi }\int_{-\frac{2}{\sqrt{3}}}^{2\sqrt{3}}\frac{x}{4+x^{2}}dx\)
=\(\frac{4}{\pi }\left [ \frac{1}{2}\ln \left | 4+x^{2} \right | \right ]_{-\frac{2}{\sqrt{3}}}^{2\sqrt{3}}\)
=\(\frac{2}{\pi }\left ( \ln 16-\ln \frac{16}{3} \right )\left ( =\frac{2}{\pi }\ln 3 \right )\)
Question
The lifetime of a particular component of a solar cell is \(Y\) years, where \(Y\) is a continuous random variable with probability density function
\(f(y)=\left\{\begin{matrix}
0, & when\ y<0
\\0.5e^{-y/2}, & when\ y\geq 0
\end{matrix}\right.\)
(a) Find the probability, correct to four significant figures, that a given component fails within six months.
Each solar cell has three components which work independently and the cell will continue to run if at least two of the components continue to work.
(b) Find the probability that a solar cell fails within six months.
Answer/Explanation
Ans
(a) Required probability= \(P(Y\leq \frac{1}{2})=\int_{0}^{1/2}0.5e^{-y/2}dy=0.2212\).
OR
Required probability= \(\int_{0}^{1/2}0.5e^{-y/2}dy=-\left [ e^{-y/2} \right ]_{0}^{1/2}=1-e^{-1/4}=0.2212\)
(b) Required probability= P(2 or 3 of the components fail in six months) = \(0.125\).
Question
The probability density function of the random variable \(X\) is given by
\(f(x)=\left\{\begin{matrix}
\frac{k}{\sqrt{4-x^{2}}}, & for\ 0\leq x\leq 1
\\0, & otherwise
\end{matrix}\right.\)
(a) Find the value of the constant \(k\).
(b) Show that \(E(X)=\frac{6(2-\sqrt{3})}{\pi }\).
(c) Determine whether the median of \(X\) is less than \(\frac{1}{2}\) or greater than \(\frac{1}{2}\)
Answer/Explanation
Ans
(a) Using \(\int_{0}^{1}f(x)dx=1\Rightarrow k\int_{0}^{1}\frac{dx}{\sqrt{4-x^{2}}}=1\)
\(k\left [ arcsin\frac{x}{2} \right ]_{0}^{1}=1\Rightarrow k\left ( arcsin\left ( \frac{1}{2}-arcsin(0) \right ) \right )=1\)
\(k\frac{\pi }{6}=1\Rightarrow k=\frac{6}{\pi }\)
(b) \(E(X)=\frac{6}{\pi }\int_{0}^{1}\frac{xdx}{\sqrt{4-x^{2}}}\)
Let \(u=4-x^{2} \frac{\mathrm{d} u}{\mathrm{d} x}=-2x\)
When \(x=0, u=4\) When \(x=1, u=3\)
\(E(X)=-\frac{6}{\pi }\times \frac{1}{2}\int_{4}^{3}\frac{du}{u\tfrac{1}{2}}=-\frac{6}{\pi }\left [ u^{\frac{1}{2}} \right ]_{4}^{3}=\frac{6}{\pi }(2-\sqrt{3})\)
(c) The median \(m\) satisfies
\(\frac{6}{\pi }\int_{0}^{m}\frac{dx}{\sqrt{4-x^{2}}}=\frac{1}{2}\Rightarrow \frac{6}{\pi }\left [arcsin\left (\frac{x}{2} \right )\right ]_{0}^{m}=\frac{1}{2}\)
\(\Rightarrow \left ( \frac{m}{2} \right )=\frac{\pi }{12}\Rightarrow m=2\sin \left ( \frac{\pi }{12} \right )\)
We need to determine whether \(2\sin \frac{\pi }{12}>\) or \(<\frac{1}{2}\)
Consider the graph of \(y = \sin x\)
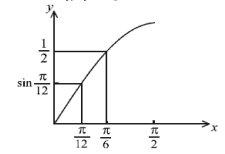
Since the graph of \(y = sin x\) or \(0\leq x\leq \frac{\pi }{2}\) is concave downwards and \(\sin \frac{\pi }{6}=\frac{1}{2}\)
it follows by inspection that \(\sin \frac{\pi }{12}>\frac{1}{4}\), hence \(m=2\sin \frac{\pi }{12}>\frac{1}{2}\)
Question
(a) Use integration by parts to show that
\(\int 2x\ arctan\ xdx=(x^{2}+1)arctan\ x-x+C\), where \(C\) is a constant.
(b) The probability density function of the random variable \(X\) is defined by
\(f(x)=\left\{\begin{matrix}
\frac{\pi }{2}-2x\ arctan\ x, & 0\leq x\leq 1
\\0, & otherwise
\end{matrix}\right.\)
The value of a is such that \(P(X<a)=\frac{3}{4}\).
(i) Show that \(a\) satisfies the equation \(a(2\pi +4)=3+4(a^{2}+1)arctan\ a\).
(ii) Find the value of \(a\).
Answer/Explanation
Ans
(a) \(\int 2x\ arctan\ xdx\)
\(u=arctan\ x, v=x^{2}\)
\(du=\frac{1}{1+x^{2}}dx dv=2x\ dx\)
\(\int 2x\ arctan\ dx=x^{2}arctan\ x-\int \frac{x^{2}}{1+x^{2}}dx\)
\(=x^{2}arctan\ x-x+arctan\ x+C\)
\(=(x^{2}+1)arctan\ x-x+C\)
(b) (i) \(\int_{0}^{a}\left ( \frac{\pi }{2} -2x\arctan x\right )dx=\frac{3}{4}\)
\(\left [ \frac{\pi }{2}x-(x^{2}+1)arctan\ x+x \right ]_{0}^{a}=\frac{3}{4}\)
\(\frac{\pi }{2}a-(a^{2}+1)arctan\ a+a=\frac{3}{4}\)
\(2\pi a-4(a^{2}+1)arctan\ a+4a=3\)
\(a(2\pi +4)=3+4(a^{2}+1)arctan\ a\)
(ii) \(a=0.541\)
Question
The continuous random variable X has probability density function f (x) where
\(f_{k}(x)=\left\{\begin{matrix}
e-ke^{kx}, & 0\leq x\leq 1
\\0, & otherwise
\end{matrix}\right.\)
(a) Show that \(k = 1\).
(b) What is the probability that the random variable \(X\) has a value that lies between \(\frac{1}{4}\) and \(\frac{1
{2}\)? Give your answer in terms of \(e\).
(c) Find the mean and variance of the distribution. Give your answers exactly, in terms of \(e\). The random variable
(X\) above represents the lifetime, in years, of a certain type of battery.
(d) Find the probability that a battery lasts more than six months.
A calculator is fitted with three of these batteries. Each battery fails independently of the other two. Find the
probability that at the end of six months
(e) none of the batteries has failed;
(f) exactly one of the batteries has failed.
Answer/Explanation
Ans
(a) For \(f(x)\) to be a probability distribution function, \(\int_{0}^{1}f(x)dx=1.\)
\(\Rightarrow \int_{0}^{1}\left ( e-ke^{kx} \right )dx=1\Rightarrow \left [ ex-e^{kx} \right ]_{0}^{1}=1\)
\(\Rightarrow e-e^{k}+1=1\Rightarrow e=e^{k}\Rightarrow k=1\)
Thus \(f(x)=e-e^{x},0\leq x\leq 1\)
(b) \(\int_{1/4}^{1/2}(e-e^{x})dx=\left [ ex-e^{x} \right ]_{1/4}^{1/2}=\frac{e}{2}-\sqrt{e}-\frac{e}{4}+\sqrt[4]{e}=\frac{e}{4}-\sqrt{e}+\sqrt[4]{e}\)
(c) \(\mu =\int_{0}^{1}(e-e^{x})dx=\int_{0}^{1}(ex-xe^{x})dx\)
=\(\left [ \frac{ex^{2}}{2} \right ]_{0}^{1}-\int_{0}^{1}xe^{x}dx=\frac{e}{2}-\left [ xe-e^{x} \right ]_{0}^{1}=\frac{e}{2}-1\)
Variance=\(\int_{0}^{1}x^{2}(e-e^{x})dx-\left ( \frac{e}{2}-1 \right )^{2}\)
=\(\left [ \frac{ex^{3}}{3}-e^{x}(x^{2}-2x+2) \right ]_{0}^{1}-\left ( \frac{e}{2}-1 \right )^{2}\)
=\(2-\frac{2}{3}e-\frac{e^{2}}{4}+e-1=1+\frac{e}{3}-\frac{e^{2}}{4}\)
(d) \(p\)(battery lasts more than \(6\) months) = \(p (x > 1/2)\)
\(=\int_{1/2}^{1}(e-e^{x})dx=\left [ ex-e^{x} \right ]_{1/2}^{1}=\sqrt{e}-\frac{e}{2}\) or \(0.290\)
(e) \(p\)(no battery failed) = \(p\)(all lasted more than \(6\) months) =\(\left ( \sqrt{e}-\frac{e}{2} \right )^{3} or 0.0243\)
(f) \(p\)(exactly one battery failed)= \(0.179\)
Question
A company produces computer microchips, which have a life expectancy that follows a normal distribution with a mean of \(90\) months and a standard deviation of \(3.7\) months.
(a) If a microchip is guaranteed for \(84\) months find the probability that it will fail before the guarantee ends.
(b) The probability that a microchip does not fail before the end of the guarantee is required to be \(99\)%. For how
many months should it be guaranteed?
(c) A rival company produces microchips where the probability that they will fail after \(84\) months is \(0.88\). Given
that the life expectancy also follows a normal distribution with standard deviation \(3.7\) months, find the mean.
Answer/Explanation
Ans
(a) \(P(X\leq 84)=0.0524\)
(b) \(x=81.4 (accept 81)\)
(c) \(P(X\leq 84)=0.12\Rightarrow z=-1.1749…\)
mean is \(88.3\) (accept 88)
Question
The times taken for buses travelling between two towns are normally distributed with a mean of \(35\) minutes and standard deviation of \(7\) minutes.
(a) Find the probability that a randomly chosen bus completes the journey in less than \(40\) minutes.
(b) \(90\)% of buses complete the journey in less than \(t\) minutes. Find the value of \(t\).
(c) A random sample of \(10\) buses had their travel time between the two towns recorded. Find the probability that
exactly \(6\) of these buses complete the journey in less than \(40\) minutes.
Answer/Explanation
Ans
(a) \(P(T\ <84)=0.762\) [ use Ncd]
(b) \(P(T\ < t)=0.90\Rightarrow t=44.0\) (min) [ use InvN ]
(c) \(X\sim B(10,0.762…)\)
\(P(X=6)=0.131\)
Question
(a) A box of biscuits is considered to be underweight if it weighs less than \(228\) grams. It is known that the weights of these boxes of biscuits are normally distributed with a mean of \(231\)
grams and a standard deviation of \(1.5\) grams. What is the probability that a box is underweight?
(b) The manufacturer decides that the probability of a box being underweight should be reduced to \(0.002\).
(i) Bill’s suggestion is to increase the mean and leave the standard deviation unchanged. Find the value of the new mean.
(ii) Sarah’s suggestion is to reduce the standard deviation and leave the mean unchanged. Find the value of the new standard deviation.
(c) After the probability of a box being underweight has been reduced to \(0.002\), a group of customers buys 100 boxes of biscuits. Find the probability that at least two of the boxes are underweight.
Answer/Explanation
Ans
(a) \(X\sim N(231, 1.5^{2})\)
\(P(X<228)=0.0228\)
(b) (i) \(X\sim N(\mu ,1.5^{2})\)
\(P(X<228)=0.002\) \(\frac{228-\mu }{1.5}=-2.878…\)
\(\mu =232 grams\)
(ii) \(X\sim N(231,\sigma ^{2})\)
\(\frac{228-231 }{\sigma }=-2.878…\)
\(\sigma =1.04\) grams
(c) \(X\sim B(100,0.002)\)
\(P(X\geq 2)=0.0174\)
Question
A machine is set to produce bags of salt, whose weights are distributed normally, with a mean of \(110\) g and standard deviation of \(1.142\) g. If the weight of a bag of salt is less than \(108\) g, the bag is rejected. With these settings, \(4\)% of the bags are rejected. The settings of the machine are altered and it is found that \(7\)% of the bags are rejected.
(a) (i) If the mean has not changed, find the new standard deviation, correct to three decimal places. The machine is adjusted to operate with this new value of the standard deviation.
(ii) Find the value, correct to two decimal places, at which the mean should be set so that only \(4\)% of the bags are rejected.
(b) With the new settings from part (a), it is found that \(80\)% of the bags of salt have a weight which lies between Ag and Bg, where A and B are symmetric about the mean. Find the values of A and B, giving your answers correct to two decimal places.
Answer/Explanation
Ans
(a) (i) Let \(X\) be the random variable “the weight of a bag of salt”.
Then \(X\sim N(110,\sigma ^{2})\), where σ is the new standard deviation.
Given \(P(X<108)=0.07,let Z=\frac{X-110}{\sigma }\)
Then \(P\left ( Z<\frac{108-110}{\sigma } \right )=0.07\)
Therefore, \(\frac{-2}{\sigma}=-1.476\Rightarrow \sigma =1.355\)
(ii) Let the new mean be \(\mu , then X\sim N(\mu , 1.355^{2})\).
Then \(\left ( Z<\frac{108-\mu }{1.355} \right )=0.04\)
Therefore, \(\frac{108-\mu }{1.355}=1.751\Rightarrow \mu =110.37\)
(b) If the mean is \(110.37\) g then
\(X\sim (110.37,1.355), P(A<X<B)=0.8\)
Then \(P(X<A)=0.1, and P(X<B)=0.9\).
Therefore, \(\frac{A-110.37}{1.355}=-1.282\Rightarrow A=108.63\)
Therefore, \(\frac{B-110.37}{1.355}=-1.282\Rightarrow B=112.11\)
Question
A company buys \(44\)% of its stock of bolts from manufacturer A and the rest from manufacturer B. The diameters of the bolts produced by each manufacturer follow a normal distribution with a standard deviation of \(0.16\) mm. The mean diameter of the bolts produced by manufacturer A is \(1.56\) mm. \(24.2\)% of the bolts produced by manufacturer B have a diameter less than \(1.52\) mm.
(a) Find the mean diameter of the bolts produced by manufacturer B. A bolt is chosen at random from the company’s stock.
(b) Show that the probability that the diameter is less than \(1.52\) mm is \(0.312\), to three significant figures.
(c) The diameter of the bolt is found to be less than \(1.52\) mm. Find the probability that the bolt was produced by manufacturer B.
(d) Manufacturer B makes \(8000\) bolts in one day. It makes a profit of $ \(1.50\) on each bolt sold, on condition that its diameter measures between \(1.52\)mm and \(1.83\) mm. Bolts
whose diameters measure less than \(1.52\) mm must be discarded at a loss of \($ 0.85\) per bolt. Bolts whose diameters measure over 1.83 mm are sold at a reduced profit of \($ 0.50\)
per bolt.
Find the expected profit for manufacturer B.
Answer/Explanation
Ans
(a) Let B be the random variable “diameter of the bolts produced by manufacturer B”.
\(\Rightarrow P(B<1.52)=0.242\Rightarrow P\left ( Z<\frac{1.52-\mu }{0.16} \right )=0.242\)
\(\frac{1.52-\mu }{0.16}=-0.69988 \Rightarrow \mu =1.63\)
(b) Let \(A\) be the random variable “diameter of the bolts produced by manufacturer \(A\)”.
\(\Rightarrow P(A<1.52):=0.40129 (0.4013)\)
P(diameter less than \(1.52\) mm)=\(0.44\times 0.40129+0.56\times \times 0.242=0.312\)
(c) P (bolt produced by B|d<1.52)=\(\frac{0.242\times 0.56}{0.31209}=0.434\)
(d) \(P(B>1.83)=0.10564\)
\(P(1.52<B<1.83)=0,65236\)
Expected gain=\(\$ 8000(0.242\times (-0.85)+0.65236\times 1.50+0.10564\times 0.50) =\$ 6605.28\)
Question
Ian and Karl have been chosen to represent their countries in the Olympic discus throw. Assume that the distance thrown by each athlete is normally distributed. The mean distance thrown by Ian in the past year was \(60.33\) m with a standard deviation of \(1.95\) m.
(a) In the past year, \(80\)% of Ian’s throws have been longer than \(x\) metres. Find \(x\), correct to two decimal places.
(b) In the past year, \(80\)% of Karl’s throws have been longer than \(56.52\) m. If the mean distance of his throws was \(59.39\) m, find the standard deviation of his throws, correct to two decimal places.
(c) This year, Karl’s throws have a mean of \(59.50\) m and a standard deviation of \(3.00\) m. Ian’s throws still have a mean of \(60.33\) m and standard deviation \(1.95\) m. In a competition an athlete must have at least one throw of \(65\) m or more in the first round to qualify for the final round. Each athlete is allowed three throws in the first round.
(i) Determine which of these two athletes is more likely to qualify for the final on their first throw.
(ii) Find the probability that both athletes qualify for the final.
Answer/Explanation
Ans
(a) \(X\)=length of Ian’s throw. \(X\sim N(60.33,1.95^{2})\)
\(P(X>x)=0.80\Rightarrow x=58.69 m\)
(b) Y = length of Karl’s throw.
\(Y\sim N(59.39,\sigma ^{2})\)
\(P(Y>56.52)=0.80\Rightarrow z=-0.8416\)
\(-0.8416=\frac{56.52-59.39}{\sigma }\)
\(\sigma =3.41 (accept 3.42)\)
(c) (i) \(Y\sim N(59.50,3.00 ^{2})\) \(X\sim N(60.33,1.95 ^{2})\)
\(P(Y\geq 65)=0.0334\) \(P(X\geq 65)=0.00831\) (no(AP)here)
THEN
Karl is more likely to qualify since \(P(Y\geq 65)>P(X\geq 65)\)
(ii) Therefore P(Ian qualifies) = \(0.0247\)
P (Karl qualifies) = \(0.0969\)
Assuming independence
P(both qualify) = \((0.0247)(0.0969) = 0.00239\)
Question
[with GDC]
The graph shows a normal curve for the random variable X, with mean μ and standard deviation σ.

It is known that \(p (X > 12) = 0.1\).
(a) The shaded region \(A\) is the region under the curve where \(x > 12\). Write down the area of the shaded region \(A\).
It is also known that \(p (X < 8) = 0.1\).
(b) Find the value of \(μ\), explaining your method in full.
(c) Show that \(σ = 1.56\) to an accuracy of three significant figures.
(d) Find \(p (X < 11)\).
Answer/Explanation
Ans
(a) Area \(A = 0.1\)
(b) EITHER Since \(p(X\geq 12)= p(X\leq 8)\),
then \(8\) and \(12\) are symmetrical about the mean.
Thus mean = \(\frac{8+12}{2}=10\)
OR
\(\frac{12-\mu }{\sigma }=\frac{\mu -8}{\sigma }\Rightarrow 12-\mu =\mu -8\Rightarrow \mu =10\)
(c) \(\left ( \frac{12-10}{\sigma } \right )=1.282\)
\(\sigma =\frac{2}{}1.282 =1.56 (3 sf)\)
(d) \(0.739 (3 sf)\)
Question
[with GDC]
The weights of chickens for sale in a shop are normally distributed with mean \(2.5\) kg and standard deviation \(0.3\) kg.
(a) A chicken is chosen at random.
(i) Find the probability that it weighs less than \(2\) kg.
(ii) Find the probability that it weighs more than \(2.8\) kg.
(iii) In the diagram below, shade the areas that represent the probabilities from parts (i) and (ii).
(iv) Find the probability that it weighs between \(2\) kg and \(2.8\) kg (\(4\)sf).
(b) A customer buys 10 chickens.
(i) Find the probability that all \(10\) chickens weigh between \(2\) kg and \(2.8\) kg.
(ii) Find the probability that at least \(7\) of the chickens weigh between \(2\) kg and \(2.8\) kg.
Answer/Explanation
Ans
\(W\sim N(2.5, 0.3^{2})\)
(a) (i) \(0.048\) (ii) \(0.159\)
(iii) 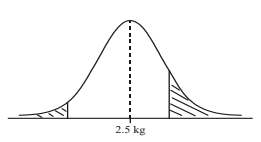
(iv) \(P = 0.7936\)
(b) (i) \(X\sim B(10, 0.7935…)\)
\(P(X=10)=(0.7935…)^{10}\) OR \(P(X = 10) = 0.0990 (3 sf)\)
(ii) \(X\sim B(10, 0.7935…)\)
\(P(X \geq 7) = 0.867\)
Question
[with GDC]
Bags of cement are labelled \(25\) kg. The bags are filled by machine and the actual weights are normally distributed with mean \(25.7\) kg and standard deviation \(0.50\) kg.
(a) What is the probability a bag selected at random will weigh less than \(25.0\) kg?
In order to reduce the number of underweight bags (bags weighing less than \(25\) kg) to \(2.5\)% of the total, the mean is increased without changing the standard deviation.
(b) Show that the increased mean is \(26.0\) kg.
It is decided to purchase a more accurate machine for filling the bags. The requirements for this machine are that only \(2.5\)% of bags be under \(25\) kg and that only \(2.5\)% of bags be over \(26\) kg.
(c) Calculate the mean and standard deviation that satisfy these requirements.
Answer/Explanation
Ans
(a) \(P(W < 25) = 0.0808\)
(b) \(\mu = 25.98 = 26.0\) (\(3\) sf)
(c) Clearly, by symmetry \(\mu = 25.5\)
\(\frac{25.0-25.5}{\sigma }=-1.96\Rightarrow 0.5=1.96\sigma \Rightarrow \sigma =0.255\) kg
Question
[with GDC]
In a large school, the heights of all fourteen-year-old students are measured.
The heights of the girls are normally distributed with mean \(155\)cm and standard deviation \(10\)cm.
The heights of the boys are normally distributed with mean \(160\)cm and standard deviation \(12\)cm.
(a) Find the probability that a girl is taller than \(170\) cm.
(b) Given that \(10\)% of the girls are shorter than \(x\) cm, find \(x\).
(c) Given that \(90\)% of the boys have heights between \(q\) cm and \(r\) cm where \(q\) and \(r\) are symmetrical about \(160\) cm, and \(q < r\), find the value of \(q\) and of \(r\).
In the group of fourteen-year-old students, \(60\)% are girls and \(40\)% are boys.
The probability that a girl is taller than \(170\) cm was found in part (a).
The probability that a boy is taller than \(170\) cm is \(0.202\).
A fourteen-year-old student is selected at random.
(d) Calculate the probability that the student is taller than \(170\) cm.
(e) Given that the student is taller than \(170\) cm, what is the probability the student is a girl?
Answer/Explanation
Ans
Girls’height \(G\sim N(155,10^{2}), Boys ‘height B\sim N(160,12^{2})\)
(a) \(P(G > 170) = 0.0668\)
(b) \(x = 142\)
(c) \(r = 180 q = 140\)
(d) \(P(H > 170 ) = 0.60\times 0.0668+0.40\times 0.202=0.12088=0.121 (3 sf)\)
(e) \(P(F|H>170)=\frac{0.60\times 0.0668}{0.121}=0.332\)