Question: [Maximum mark: 6]
A discrete random variable, X, has the following probability distribution:
| x | 0 | 1 | 2 | 3 |
| P(X = x) | 0.41 | k – 0.28 | 0.46 | 0.29 – 2k2 |
(a) Show that 2k2 – k + 0.12 = 0.
(b) Find the value of k , giving a reason for your answer.
(c) Hence, find E(X).
▶️Answer/Explanation
Ans:
(a) 0.41 + k – 0.28 + 0.46 + 0.29 – 2k2 = 1 OR k – 2k2 + 0.01 = 0.13 (or equivalent)
2k2 – k + 0.12 = 0
(b) one of 0.2 OR 0.3
k = 0.3
reasoning to reject k = 0.2 eg P(1) = k – 0.28 0 ≥ 0 therefore k ≠ 0.2
(c) attempting to use the expected value formula
E(X) = 0 × 0.41 + 1 × (0.3 – 0.28) + 2 × 0.46 + 3 ×(0.29 – 2 × 0.32)
= 1.27
Note: Award M1A0 if additional values are given.
Question
A continuous random variable X has the probability density function f given by
F (x) =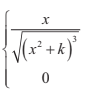 
0 ≤ x ≤ 4
where \(k\in \mathbb{R}^+\) .
Show that \(\sqrt{16+K}-\sqrt{K}= \sqrt{K}\sqrt{16+K}\) [5]
Find the value of k . [2]
▶️Answer/Explanation
Ans:
(a)
recognition of the need to integrate
\(\frac{x}{\sqrt{(x^{2}+k)^{3}}}\)
\(\int \ \frac{x}{\sqrt{(x^{2}+k)^{3}}} dx(=1)\)
EITHER
\(u= x^{2}+ k \Rightarrow \frac{du}{dx}= 2x\) (or equivalent)
(b)
attempt to solve \(\sqrt{16+k}-\sqrt{k}= \sqrt{k}\sqrt{16+k}\)
k= 0.645038… = 0.645
Question
A continuous random variable X has the probability density function f n given by
\(f_n(x)=\{\begin{matrix} (n+1)x^n;\;0\leq x\leq 1 & \\ 0 \; otherwise &\end{matrix}.\)
where n ∈ \(\mathbb{R}\) , n ≥ 0 .
(a) Show that \(E(X)=\frac{n+1}{n+2}\)
(b) Show that Var \(X=\frac{n+1}{(n+2)^2(n+3)}\)
▶️Answer/Explanation
Ans:
(a) $\begin{eqnarray} \text{E}\left(X\right) &=& \int_0^1 xf\left(x\right) \text{d}x \nonumber \\ &=& \left(n+1\right)\int_0^1 x^{n+1} \text{d}x \nonumber \\ &=& \frac{n+1}{n+2}\left[x^{n+2}\right]_0^1 \nonumber \\ &=& \frac{n+1}{n+2}. \end{eqnarray}$ (b) To obtain $\text{Var}\left(X\right)$, we need to first obtain $\text{E}\left(X^2\right)$, i.e., $\begin{eqnarray} \text{E}\left(X^2\right) &=& \int_0^1 x^2f\left(x\right) \text{d}x \nonumber \\ &=& \left(n+1\right)\int_0^1 x^{n+2} \text{d}x \nonumber \\ &=& \frac{n+1}{n+3}\left[x^{n+3}\right]_0^1 \nonumber \\ &=& \frac{n+1}{n+3}. \end{eqnarray}$ Thus, $\begin{eqnarray} \text{Var}\left(X\right) &=& \text{E}\left(X^2\right)-\left[\text{E}\left(X\right)\right]^2 \nonumber \\ &=& \frac{n+1}{n+3}-\left(\frac{n+1}{n+2}\right)^2 \nonumber \\ &=& \frac{\left(n+1\right)\left(n+2\right)^2-\left(n+2\right)^2\left(n+3\right)}{\left(n+1\right)^2\left(n+3\right)} \nonumber \\ &=& \frac{\left(n+1\right)\left(n^2+4n+4-n^2-4n-3\right)}{\left(n+2\right)^2\left(n+3\right)} \nonumber \\ &=& \frac{n+1}{\left(n+2\right)^2\left(n+3\right)}. \end{eqnarray}$
Question
A continuous random variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{12{x^2}(1 – x),}&{{\text{for }}0 \leqslant x \leqslant 1,} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the probability that X lies between the mean and the mode.
▶️Answer/Explanation
Markscheme
Attempting to find the mode graphically or by using \(f'(x) = 12x(2 – 3x)\) (M1)
\({\text{Mode}} = \frac{2}{3}\) A1
Use of \({\text{E}}(X) = \int_0^1 {xf(x){\text{d}}x} \) (M1)
\({\text{E}}(X) = \frac{3}{5}\) A1
\(\int_{\frac{3}{5}}^{\frac{2}{3}} {f(x){\text{d}}x = 0.117\,\,\,\,\,\left( { = \frac{{1981}}{{16\,{\text{875}}}}} \right)} \) M1A1 N4
[6 marks]