Question: [Maximum mark: 6]
A discrete random variable, X, has the following probability distribution:
| x | 0 | 1 | 2 | 3 |
| P(X = x) | 0.41 | k – 0.28 | 0.46 | 0.29 – 2k2 |
(a) Show that 2k2 – k + 0.12 = 0.
(b) Find the value of k , giving a reason for your answer.
(c) Hence, find E(X).
Answer/Explanation
Ans:
(a) 0.41 + k – 0.28 + 0.46 + 0.29 – 2k2 = 1 OR k – 2k2 + 0.01 = 0.13 (or equivalent)
2k2 – k + 0.12 = 0
(b) one of 0.2 OR 0.3
k = 0.3
reasoning to reject k = 0.2 eg P(1) = k – 0.28 0 ≥ 0 therefore k ≠ 0.2
(c) attempting to use the expected value formula
E(X) = 0 × 0.41 + 1 × (0.3 – 0.28) + 2 × 0.46 + 3 ×(0.29 – 2 × 0.32)
= 1.27
Note: Award M1A0 if additional values are given.
Question
The probability distribution of a discrete random variable X is defined by
\({\text{P}}(X = x) = cx(5 – x),{\text{ }}x = {\text{1, 2, 3, 4}}\) .
(a) Find the value of c.
(b) Find E(X) .
Answer/Explanation
Markscheme
(a) Using \(\sum {{\text{P}}(X = x) = 1} \) (M1)
\(4c + 6c + 6c + 4c = 1\,\,\,\,\,(20c = 1)\) A1
\(c = \frac{1}{{20}}\,\,\,\,\,( = 0.05)\) A1 N1
(b) Using \({\text{E}}(X) = \sum {x{\text{P}}(X = x)} \) (M1)
\( = (1 \times 0.2) + (2 \times 0.3) + (3 \times 0.3) + (4 \times 0.2)\) (A1)
\( = 2.5\) A1 N1
Notes: Only one of the first two marks can be implied.
Award M1A1A1 if the x values are averaged only if symmetry is explicitly mentioned.
[6 marks]
Examiners report
This question was generally well done, but a few candidates tried integration for part (b).
Question
John removes the labels from three cans of tomato soup and two cans of chicken soup in order to enter a competition, and puts the cans away. He then discovers that the cans are identical, so that he cannot distinguish between cans of tomato soup and chicken soup. Some weeks later he decides to have a can of chicken soup for lunch. He opens the cans at random until he opens a can of chicken soup. Let Y denote the number of cans he opens.
Find
(a) the possible values of Y ,
(b) the probability of each of these values of Y ,
(c) the expected value of Y .
Answer/Explanation
Markscheme
(a) 1, 2, 3, 4 A1
(b) \({\text{P}}(Y = 1) = \frac{2}{5}\) A1
\({\text{P}}(Y = 2) = \frac{3}{5} \times \frac{2}{4} = \frac{3}{{10}}\) A1
\({\text{P}}(Y = 3) = \frac{3}{5} \times \frac{2}{4} \times \frac{2}{3} = \frac{1}{5}\) A1
\({\text{P}}(Y = 4) = \frac{3}{5} \times \frac{2}{4} \times \frac{1}{3} \times \frac{2}{2} = \frac{1}{{10}}\) A1
(c) \({\text{E}}(Y) = 1 \times \frac{2}{5} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{5} + 4 \times \frac{1}{{10}}\) M1
\( = 2\) A1
[7 marks]
Examiners report
Candidates found this question challenging with only better candidates gaining the correct answers. A number of students assumed incorrectly that the distribution was either Binomial or Geometric.
Question
A random variable has a probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{kx(2 – x),}&{0 \leqslant x \leqslant 2} \\
{0,}&{{\text{elsewhere}}{\text{.}}}
\end{array}} \right.\]
(a) Show that \(k = \frac{3}{4}\) .
(b) Find \({\text{E}}(X)\) .
Answer/Explanation
Markscheme
(a) \(\int_0^2 {kx(2 – x){\text{d}}x = 1} \) M1A1
Note: Award M1 for LHS and A1 for setting = 1 at any stage.
\(\left[ {\frac{{2k}}{2}{x^2} – \frac{k}{3}{x^3}} \right]_0^2 = 1\) A1
\(k\left( {4 – \frac{8}{3}} \right) = 1\) A1
\(k = \frac{3}{4}\) AG
(b) \({\text{E}}(X) = \frac{3}{4}\int_0^2 {{x^2}(2 – x){\text{d}}x} \) (M1)
= 1 A1
Note: Accept answers that indicate use of symmetry.
[6 marks]
Examiners report
The integration was particularly well done in this question. A number of students treated the distribution as discrete. On the whole a) was done well once the distribution was recognized although there was a certain amount of fudging to achieve the result. A significant number of students did not initially set the integral equal to 1. Very few noted the symmetry of the distribution in b).
Question
A continuous random variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{0,}&{x < 0} \\
{a{{\text{e}}^{ – ax}},}&{x \geqslant 0.}
\end{array}} \right.\]
It is known that \({\text{P}}(X < 1) = 1 – \frac{1}{{\sqrt 2 }}\).
(a) Show that \(a = \frac{1}{2}\ln 2\).
(b) Find the median of X.
(c) Calculate the probability that X < 3 given that X >1.
Answer/Explanation
Markscheme
(a) \(\int_0^1 {a{{\text{e}}^{ – ax}}} {\text{d}}x = 1 – \frac{1}{{\sqrt 2 }}\) M1A1
\(\left[ { – {{\text{e}}^{ – ax}}} \right]_0^1 = 1 – \frac{1}{{\sqrt 2 }}\) M1A1
\( – {{\text{e}}^{ – a}} + 1 = 1 – \frac{1}{{\sqrt 2 }}\) A1
Note: Accept \({{\text{e}}^0}\) instead of 1.
\({{\text{e}}^{ – a}} = \frac{1}{{\sqrt 2 }}\)
\({{\text{e}}^a} = \sqrt 2 \)
\(a = \ln {2^{\frac{1}{2}}}\,\,\,\,\,\left( {{\text{accept }} – a = \ln {2^{ – \frac{1}{2}}}} \right)\) A1
\(a = \frac{1}{2}\ln 2\) AG
[6 marks]
(b) \(\int_0^M {a{{\text{e}}^{ – ax}}{\text{d}}x = \frac{1}{2}} \) M1A1
\(\left[ { – {{\text{e}}^{ – ax}}} \right]_0^M = \frac{1}{2}\) A1
\( – {{\text{e}}^{ – Ma}} + 1 = \frac{1}{2}\)
\({{\text{e}}^{ – Ma}} = \frac{1}{2}\) A1
\(Ma = \ln 2\)
\(M = \frac{{\ln 2}}{a} = 2\) A1
[5 marks]
(c) \({\text{P}}(1 < X < 3) = \int_1^3 {a{{\text{e}}^{ – ax}}{\text{d}}x} \) M1A1
\( = – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}\) A1
\({\text{P}}(X < 3|X > 1) = \frac{{{\text{P}}(1 < X < 3)}}{{{\text{P}}(X > 1)}}\) M1A1
\( = \frac{{ – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}}}{{1 – {\text{P}}(X < 1)}}\) A1
\( = \frac{{ – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}}}}{{\frac{1}{{\sqrt 2 }}}}\) A1
\( = \sqrt 2 ( – {{\text{e}}^{ – 3a}} + {{\text{e}}^{ – a}})\)
\( = \sqrt 2 \left( { – {2^{ – \frac{3}{2}}} + {2^{ – \frac{1}{2}}}} \right)\) A1
\( = \frac{1}{2}\) A1
Note: Award full marks for \({\text{P}}(X < 3/X > 1) = {\text{P}}(X < 2) = \frac{1}{2}\) or quoting properties of exponential distribution.
[9 marks]
Total [20 marks]
Examiners report
Many candidates did not attempt this question and many others were clearly not familiar with this topic. On the other hand, most of the candidates who were familiar with continuous random variables and knew how to start the questions were successful and scored well in parts (a) and (b). The most common errors were in the integral of \({e^{ – at}}\), having the limits from \( – \infty \) to 1, confusion over powers and signs (‘-’ sometimes just disappeared). Understanding of conditional probability was poor and marks were low in part (c). A small number of candidates from a small number of schools coped very competently with the algebra throughout the question.
Question
A continuous random variable X has the probability density function f given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{c(x – {x^2}),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
(a) Determine c.
(b) Find \({\text{E}}(X)\).
Answer/Explanation
Markscheme
(a) the total area under the graph of the pdf is unity (A1)
area \( = c\int_0^1 {x – {x^2}{\text{d}}x} \)
\( = c\left[ {\frac{1}{2}{x^2} – \frac{1}{3}{x^3}} \right]_0^1\) A1
\( = \frac{c}{6}\)
\( \Rightarrow c = 6\) A1
(b) \({\text{E}}(X) = 6\int_0^1 {{x^2} – {x^3}{\text{d}}x} \) (M1)
\( = 6\left( {\frac{1}{3} – \frac{1}{4}} \right) = \frac{1}{2}\) A1
Note: Allow an answer obtained by a symmetry argument.
[5 marks]
Examiners report
Most candidates made a meaningful attempt at this question with many gaining the correct answers. One or two candidates did not attempt this question at all.
Question
A continuous random variable X has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k\sin x,}&{0 \leqslant x \leqslant \frac{\pi }{2}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the value of k.
Find \({\text{E}}(X)\).
Find the median of X.
Answer/Explanation
Markscheme
\(k\int_0^{\frac{\pi }{2}} {\sin x{\text{d}}x = 1} \) M1
\(k[ – \cos x]_0^{\frac{\pi }{2}} = 1\)
k = 1 A1
[2 marks]
\({\text{E}}(X) = \int_0^{\frac{\pi }{2}} {x\sin x{\text{d}}x} \) M1
integration by parts M1
\([ – x\cos x]_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {\cos x{\text{d}}x} \) A1A1
= 1 A1
[5 marks]
\(\int_0^M {\sin x{\text{d}}x} = \frac{1}{2}\) M1
\([ – \cos x]_0^M = \frac{1}{2}\) A1
\(\cos M = \frac{1}{2}\)
\(M = \frac{\pi }{3}\) A1
Note: accept \(\arccos \frac{1}{2}\)
[3 marks]
Examiners report
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Question
A continuous random variable X has the probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{k\sin x,}&{0 \leqslant x \leqslant \frac{\pi }{2}} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Find the value of k.
Find \({\text{E}}(X)\).
Find the median of X.
Answer/Explanation
Markscheme
\(k\int_0^{\frac{\pi }{2}} {\sin x{\text{d}}x = 1} \) M1
\(k[ – \cos x]_0^{\frac{\pi }{2}} = 1\)
k = 1 A1
[2 marks]
\({\text{E}}(X) = \int_0^{\frac{\pi }{2}} {x\sin x{\text{d}}x} \) M1
integration by parts M1
\([ – x\cos x]_0^{\frac{\pi }{2}} + \int_0^{\frac{\pi }{2}} {\cos x{\text{d}}x} \) A1A1
= 1 A1
[5 marks]
\(\int_0^M {\sin x{\text{d}}x} = \frac{1}{2}\) M1
\([ – \cos x]_0^M = \frac{1}{2}\) A1
\(\cos M = \frac{1}{2}\)
\(M = \frac{\pi }{3}\) A1
Note: accept \(\arccos \frac{1}{2}\)
[3 marks]
Examiners report
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Most candidates scored maximum marks on this question. A few candidates found k = –1.
Question
Consider the following functions:
\[f(x) = \frac{{2{x^2} + 3}}{{75}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{{\left| {3x – 4} \right|}}{{10}},{\text{ }}x \in \mathbb{R}{\text{ }}.\]
State the range of f and of g .
Find an expression for the composite function \(f \circ g(x)\) in the form \(\frac{{a{x^2} + bx + c}}{{3750}}\), where \(a,{\text{ }}b{\text{ and }}c \in \mathbb{Z}\) .
(i) Find an expression for the inverse function \({f^{ – 1}}(x)\) .
(ii) State the domain and range of \({f^{ – 1}}\) .
The domains of f and g are now restricted to {0, 1, 2, 3, 4} .
By considering the values of f and g on this new domain, determine which of f and g could be used to find a probability distribution for a discrete random variable X , stating your reasons clearly.
Using this probability distribution, calculate the mean of X .
Answer/Explanation
Markscheme
\(f(x) \geqslant \frac{1}{{25}}\) A1
\(g(x) \in \mathbb{R},{\text{ }}g(x) \geqslant 0\) A1
[2 marks]
\(f \circ g(x) = \frac{{2{{\left( {\frac{{3x – 4}}{{10}}} \right)}^2} + 3}}{{75}}\) M1A1
\( = \frac{{\frac{{2(9{x^2} – 24x + 16)}}{{100}} + 3}}{{75}}\) (A1)
\( = \frac{{9{x^2} – 24x + 166}}{{3750}}\) A1
[4 marks]
(i) METHOD 1
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\({x^2} = \frac{{75y – 3}}{2}\) M1
\(x = \sqrt {\frac{{75y – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
METHOD 2
\(y = \frac{{2{x^2} + 3}}{{75}}\)
\(x = \frac{{2{y^2} + 3}}{{75}}\) M1
\(y = \sqrt {\frac{{75x – 3}}{2}} \) (A1)
\( \Rightarrow {f^{ – 1}}(x) = \sqrt {\frac{{75x – 3}}{2}} \) A1
Note: Accept ± in line 3 for the (A1) but not in line 4 for the A1.
Award the A1 only if written in the form \({f^{ – 1}}(x) = \) .
(ii) domain: \(x \geqslant \frac{1}{{25}}\) ; range: \({f^{ – 1}}(x) \geqslant 0\) A1
[4 marks]
probabilities from \(f(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
probabilities from \(g(x)\) :
 A2
A2
Note: Award A1 for one error, A0 otherwise.
only in the case of \(f(x)\) does \(\sum {P(X = x) = 1} \) , hence only \(f(x)\) can be used as a probability mass function A2
[6 marks]
\(E(x) = \sum {x \cdot {\text{P}}(X = x)} \) M1
\( = \frac{5}{{75}} + \frac{{22}}{{75}} + \frac{{63}}{{75}} + \frac{{140}}{{75}} = \frac{{230}}{{75}}\left( { = \frac{{46}}{{15}}} \right)\) A1
[2 marks]
Examiners report
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
In (a), the ranges were often given incorrectly, particularly the range of g where the modulus signs appeared to cause difficulty. In (b), it was disappointing to see so many candidates making algebraic errors in attempting to determine the expression for \(f \circ g(x)\). Many candidates were unable to solve (d) correctly with arithmetic errors and incorrect reasoning often seen. Since the solution to (e) depended upon a correct choice of function in (d), few correct solutions were seen with some candidates even attempting to use integration, inappropriately, to find the mean of X.
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The continuous random variable X has probability density function given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{a{e^{ – x}},}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
State the mode of X .
Determine the value of a .
Find E(X ) .
Answer/Explanation
Markscheme
0 A1
[1 mark]
\(\int_0^1 {f(x)dx = 1} \) (M1)
\( \Rightarrow a = \frac{1}{{\int_0^1 {{e^{ – x}}dx} }}\)
\( \Rightarrow a = \frac{1}{{\left[ { – {e^{ – x}}} \right]_0^1}}\)
\( \Rightarrow a = \frac{e}{{e – 1}}\) (or equivalent) A1
Note: Award first A1 for correct integration of \(\int {{e^{ – x}}dx} \) .
This A1 is independent of previous M mark.
[3 marks]
\({\text{E}}(X) = \int_0^1 {xf(x)dx\left( { = a\int_0^1 {x{e^{ – x}}dx} } \right)} \) M1
attempt to integrate by parts M1
\( = a\left[ { – x{e^{ – x}} – {e^{ – x}}} \right]_0^1\) (A1)
\( = a\left( {\frac{{e – 2}}{e}} \right)\)
\( = \frac{{e – 2}}{{e – 1}}\) (or equivalent) A1
[4 marks]
Examiners report
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
A range of answers were seen to part a), though many more could have gained the mark had they taken time to understand the shape of the function. Part b) was done well, as was part c). In c), a number of candidates integrated by parts, but found the incorrect expression \( – x{e^{ – x}} + {e^{ – x}}\).
Question
The discrete random variable X has probability distribution:
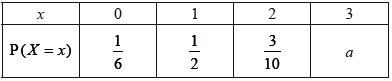
(a) Find the value of a.
(b) Find \({\text{E}}(X)\).
(c) Find \({\text{Var}}(X)\).
Answer/Explanation
Markscheme
(a) \(\frac{1}{6} + \frac{1}{2} + \frac{3}{{10}} + a = 1 \Rightarrow a = \frac{1}{{30}}\) A1
(b) \({\text{E}}(X) = \frac{1}{2} + 2 \times \frac{3}{{10}} + 3 \times \frac{1}{{30}}\) M1
\(= \frac{6}{5}\) A1
Note: Do not award FT marks if a is outside [0, 1].
[2 marks]
(c) \({\text{E}}({X^2}) = \frac{1}{2} + {2^2} \times \frac{3}{{10}} + {3^2} \times \frac{1}{{30}} = 2\) (A1)
attempt to apply \({\text{Var}}(X) = {\text{E}}({X^2}) – {\left( {{\text{E}}(X)} \right)^2}\) M1
\(\left( { = 2 – \frac{{36}}{{25}}} \right) = \frac{{14}}{{25}}\) A1
[3 marks]
Total [6 marks]
Examiners report
This was very well answered and many fully correct solutions were seen. A small number of candidates made arithmetic mistakes in part a) and thus lost one or two accuracy marks. A few also seemed unaware of the formula \({\text{Var}}(X) = {\text{E}}({X^2}) – {\text{E}}{(X)^2}\) and resorted to seeking an alternative, sometimes even attempting to apply a clearly incorrect \({\text{Var}}(X) = \sum {{{({x_i} – \mu )}^2}} \).
Question
Four numbers are such that their mean is 13, their median is 14 and their mode is 15. Find the four numbers.
Answer/Explanation
Markscheme
using the sum divided by 4 is 13 M1
two of the numbers are 15 A1
(as median is 14) we need a 13 A1
fourth number is 9 A1
numbers are 9, 13, 15, 15 N4
[4 marks]
Examiners report
Question
The continuous variable X has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{12{x^2}(1 – x),}&{0 \leqslant x \leqslant 1} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Determine \({\text{E}}(X)\) .
Determine the mode of X .
Answer/Explanation
Markscheme
\({\text{E}}(X) = \int_0^1 {12{x^3}(1 – x){\text{d}}x} \) M1
\( = 12\left[ {\frac{{{x^4}}}{4} – \frac{{{x^5}}}{5}} \right]_0^1\) A1
\( = \frac{3}{5}\) A1
[3 marks]
\(f'(x) = 12(2x – 3{x^2})\) A1
at the mode \(f'(x) = 12(2x – 3{x^2}) = 0\) M1
therefore the mode \( = \frac{2}{3}\) A1
[3 marks]
Examiners report
[N/A]
[N/A]