Question
Consider the curve with equation \({x^3} + {y^3} = 4xy\).
The tangent to this curve is parallel to the \(x\)-axis at the point where \(x = k,{\text{ }}k > 0\).
a.Use implicit differentiation to show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{4y – 3{x^2}}}{{3{y^2} – 4x}}\).[3]
b.Find the value of \(k\).[5]
▶️Answer/Explanation
Markscheme
\(3{x^2} + 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4\left( {y + x\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)\) M1A1
\((3{y^2} – 4x)\frac{{{\text{d}}y}}{{{\text{d}}x}} = 4y – 3{x^2}\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{4y – 3{x^2}}}{{3{y^2} – 4x}}\) AG
[3 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow 4y – 3{x^2} = 0\) (M1)
substituting \(x = k\) and \(y = \frac{3}{4}{k^2}\) into \({x^3} + {y^3} = 4xy\) M1
\({k^3} + \frac{{27}}{{64}}{k^6} = 3{k^3}\) A1
attempting to solve \({k^3} + \frac{{27}}{{64}}{k^6} = 3{k^3}\) for \(k\) (M1)
\(k = 1.68{\text{ }}\left( { = \frac{4}{3}\sqrt[3]{2}} \right)\) A1
Note: Condone substituting \(y = \frac{3}{4}{x^2}\) into \({x^3} + {y^3} = 4xy\) and solving for \(x\).
Question
Consider the curve defined by the equation \(4{x^2} + {y^2} = 7\).
a.Find the equation of the normal to the curve at the point \(\left( {1,{\text{ }}\sqrt 3 } \right)\).[6]
b.Find the volume of the solid formed when the region bounded by the curve, the \(x\)-axis for \(x \geqslant 0\) and the \(y\)-axis for \(y \geqslant 0\) is rotated through \(2\pi \) about the \(x\)-axis.[3]
▶️Answer/Explanation
Markscheme
METHOD 1
\(4{x^2} + {y^2} = 7\)
\(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (M1)(A1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{y}\)
Note: Award M1A1 for finding \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2.309 \ldots \) using any alternative method.
hence gradient of normal \( = \frac{y}{{4x}}\) (M1)
hence gradient of normal at \(\left( {1,{\text{ }}\sqrt 3 } \right)\) is \(\frac{{\sqrt 3 }}{4}\,\,\,( = 0.433)\) (A1)
hence equation of normal is \(y – \sqrt 3 = \frac{{\sqrt 3 }}{4}(x – 1)\) (M1)A1
\(\left( {y = \frac{{\sqrt 3 }}{4}x + \frac{{3\sqrt 3 }}{4}} \right)\,\,\,(y = 0.433x + 1.30)\)
METHOD 2
\(4{x^2} + {y^2} = 7\)
\(y = \sqrt {7 – 4{x^2}} \) (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{{\sqrt {7 – 4{x^2}} }}\) (A1)
Note: Award M1A1 for finding \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2.309 \ldots \) using any alternative method.
hence gradient of normal \( = \frac{{\sqrt {7 – 4{x^2}} }}{{4x}}\) (M1)
hence gradient of normal at \(\left( {1,{\text{ }}\sqrt 3 } \right)\) is \(\frac{{\sqrt 3 }}{4}\,\,\,( = 0.433)\) (A1)
hence equation of normal is \(y – \sqrt 3 = \frac{{\sqrt 3 }}{4}(x – 1)\) (M1)A1
\(\left( {y = \frac{{\sqrt 3 }}{4}x + \frac{{3\sqrt 3 }}{4}} \right)\,\,\,(y = 0.433x + 1.30)\)
[6 marks]
Use of \(V = \pi \int\limits_0^{\frac{{\sqrt 7 }}{2}} {{y^2}{\text{d}}x} \)
\(V = \pi \int\limits_0^{\frac{{\sqrt 7 }}{2}} {\left( {7 – 4{x^2}} \right){\text{d}}x} \) (M1)(A1)
Note: Condone absence of limits or incorrect limits for M mark.
Do not condone absence of or multiples of \(\pi \).
\( = 19.4\,\,\,\left( { = \frac{{7\sqrt 7 \pi }}{3}} \right)\) A1
[3 marks]
Question
Consider the function \(f(x) = \frac{{\sqrt x }}{{\sin x}},{\text{ }}0 < x < \pi \).
Consider the region bounded by the curve \(y = f(x)\), the \(x\)-axis and the lines \(x = \frac{\pi }{6},{\text{ }}x = \frac{\pi }{3}\).
a.i.Show that the \(x\)-coordinate of the minimum point on the curve \(y = f(x)\) satisfies the equation \(\tan x = 2x\).[5]
a.ii.Determine the values of \(x\) for which \(f(x)\) is a decreasing function.[2]
b.Sketch the graph of \(y = f(x)\) showing clearly the minimum point and any asymptotic behaviour.[3]
c.Find the coordinates of the point on the graph of \(f\) where the normal to the graph is parallel to the line \(y = – x\).[4]
d.This region is now rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume of revolution.[3]
▶️Answer/Explanation
Markscheme
attempt to use quotient rule or product rule M1
\(f’(x) = \frac{{\sin x\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \sqrt x \cos x}}{{{{\sin }^2}x}}{\text{ }}\left( { = \frac{1}{{2\sqrt x \sin x}} – \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}} \right)\) A1A1
Note: Award A1 for \(\frac{1}{{2\sqrt x \sin x}}\) or equivalent and A1 for \( – \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}\) or equivalent.
setting \(f’(x) = 0\) M1
\(\frac{{\sin x}}{{2\sqrt x }} – \sqrt x \cos x = 0\)
\(\frac{{\sin x}}{{2\sqrt x }} = \sqrt x \cos x\) or equivalent A1
\(\tan x = 2x\) AG
[5 marks]
\(x = 1.17\)
\(0 < x \leqslant 1.17\) A1A1
Note: Award A1 for \(0 < x\) and A1 for \(x \leqslant 1.17\). Accept \(x < 1.17\).
[2 marks]
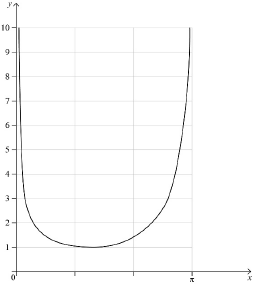
concave up curve over correct domain with one minimum point above the \(x\)-axis. A1
approaches \(x = 0\) asymptotically A1
approaches \(x = \pi \) asymptotically A1
Note: For the final A1 an asymptote must be seen, and \(\pi \) must be seen on the \(x\)-axis or in an equation.
[3 marks]
\(f’(x){\text{ }}\left( { = \frac{{\sin x\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \sqrt x \cos x}}{{{{\sin }^2}x}}} \right) = 1\) (A1)
attempt to solve for \(x\) (M1)
\(x = 1.96\) A1
\(y = f(1.96 \ldots )\)
\( = 1.51\) A1
[4 marks]
\(V = \pi \int_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{x{\text{d}}x}}{{{{\sin }^2}x}}} \) (M1)(A1)
Note: M1 is for an integral of the correct squared function (with or without limits and/or \(\pi \)).
\( = 2.68{\text{ }}( = 0.852\pi )\) A1
[3 marks]
Question
A curve C is given by the implicit equation \(x + y – {\text{cos}}\left( {xy} \right) = 0\).
The curve \(xy = – \frac{\pi }{2}\) intersects C at P and Q.
a.Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \left( {\frac{{1 + y\,{\text{sin}}\left( {xy} \right)}}{{1 + x\,{\text{sin}}\left( {xy} \right)}}} \right)\).[5]
b.i.Find the coordinates of P and Q.[4]
b.ii.Given that the gradients of the tangents to C at P and Q are m1 and m2 respectively, show that m1 × m2 = 1.[3]
c.Find the coordinates of the three points on C, nearest the origin, where the tangent is parallel to the line \(y = – x\).[7]
▶️Answer/Explanation
Markscheme
attempt at implicit differentiation M1
\(1 + \frac{{{\text{d}}y}}{{{\text{d}}x}} + \left( {y + x\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right){\text{sin}}\left( {xy} \right) = 0\) A1M1A1
Note: Award A1 for first two terms. Award M1 for an attempt at chain rule A1 for last term.
\(\left( {1 + x\,{\text{sin}}\left( {xy} \right)} \right)\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 1 – y\,{\text{sin}}\left( {xy} \right)\) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \left( {\frac{{1 + y\,{\text{sin}}\left( {xy} \right)}}{{1 + x\,{\text{sin}}\left( {xy} \right)}}} \right)\) AG
[5 marks]
EITHER
when \(xy = – \frac{\pi }{2},\,\,{\text{cos}}\,xy = 0\) M1
\( \Rightarrow x + y = 0\) (A1)
OR
\(x – \frac{\pi }{{2x}} – {\text{cos}}\left( {\frac{{ – \pi }}{2}} \right) = 0\) or equivalent M1
\(x – \frac{\pi }{{2x}} = 0\) (A1)
THEN
therefore \({x^2} = \frac{\pi }{2}\left( {x = \pm \sqrt {\frac{\pi }{2}} } \right)\left( {x = \pm 1.25} \right)\) A1
\({\text{P}}\left( {\sqrt {\frac{\pi }{2}} ,\, – \sqrt {\frac{\pi }{2}} } \right),\,\,{\text{Q}}\left( { – \sqrt {\frac{\pi }{2}} ,\,\sqrt {\frac{\pi }{2}} } \right)\) or \(P\left( {1.25,\, – 1.25} \right),\,Q\left( { – 1.25,\,1.25} \right)\) A1
[4 marks]
m1 = \( – \left( {\frac{{1 – \sqrt {\frac{\pi }{2}} \times – 1}}{{1 + \sqrt {\frac{\pi }{2}} \times – 1}}} \right)\) M1A1
m2 = \( – \left( {\frac{{1 + \sqrt {\frac{\pi }{2}} \times – 1}}{{1 – \sqrt {\frac{\pi }{2}} \times – 1}}} \right)\) A1
m1 m2 = 1 AG
Note: Award M1A0A0 if decimal approximations are used.
Note: No FT applies.
[3 marks]
(0.486,0.48
equate derivative to −1 M1
\(\left( {y – x} \right){\text{sin}}\left( {xy} \right) = 0\) (A1)
\(y = x,\,{\text{sin}}\left( {xy} \right) = 0\) R1
in the f6) A1
in the second case, \({\text{sin}}\left( {xy} \right) = 0 \Rightarrow xy = 0\) and \(x + y = 1\) (M1)
(0,1), (1,0) A1
[7 marks]