Question
Consider the curve with equation y = (2x – 1)ekx , where x ∈ R and k ∈ Q.
The tangent to the curve at the point where x = 1 is parallel to the line y = 5ekx.
Find the value of k .
▶️Answer/Explanation
Ans:
evidence of using product rule
\(\frac{dy}{dx}= (2x-1)\times \left ( ke^{kx} \right ) + 2\times e^{kx} \left ( = e^{kx}(2kx – k + 2) \right )\)
correct working for one of (seen anywhere)
\(\frac{dy}{dx} at x = 1 \Rightarrow ke^{k} + 2e^{k}\)
OR
slope of tangent is 5ek
their \(\frac{dy}{dx} at x = 1 equals the slope of y =5e^{k}x \left ( =5e^{k} \right )\) (seen anywhere)
kex + 2ek = 5ek
k = 3
Question
Consider the curve with equation y = (2x – 1)ekx , where x ∈ R and k ∈ Q.
The tangent to the curve at the point where x = 1 is parallel to the line y = 5ekx.
Find the value of k .
▶️Answer/Explanation
Ans:
evidence of using product rule
\(\frac{dy}{dx}= (2x-1)\times \left ( ke^{kx} \right ) + 2\times e^{kx} \left ( = e^{kx}(2kx – k + 2) \right )\)
correct working for one of (seen anywhere)
\(\frac{dy}{dx} at x = 1 \Rightarrow ke^{k} + 2e^{k}\)
OR
slope of tangent is 5ek
their \(\frac{dy}{dx} at x = 1 equals the slope of y =5e^{k}x \left ( =5e^{k} \right )\) (seen anywhere)
kex + 2ek = 5ek
k = 3
Question
Find the equation of the tangent to the curve y = e2x – 3x at the point where x = 0 . [Maximum mark: 5]
▶️Answer/Explanation
Ans:
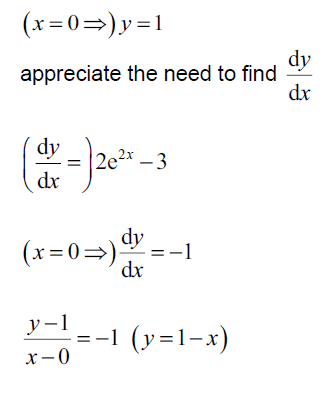
Question
Consider the functions f (x) = -(x – h)2 + 2k and g(x) = e x-2 + k where h , k ∈ R.
(a) Find f ′(x). [1]
The graphs of f and g have a common tangent at x = 3
(b) Show that h + = \(\frac{e+6}{2}\) [3]
(c) Hence, show that k = \(e+ \frac{e^{2}}{4}\) [3]
▶️Answer/Explanation
Ans
(a) f ‘( x) = −2( x − h)
(a) f (x) = -2 (x-h )
(b)
g (x) = e x-2 OR (3) = e 3-2 (may be seen anywhere)
recognizing f ‘(3) = g’ (3)
-2 (3-h ) = e 3-2 (=e)
-6+ 2h = e OR 3-h = – \(\frac{e}{2}\)
Note: The final A1 is dependent on one of the previous marks being awarded. h =\(\frac{e+6}{2}\)
(c) f( 3) = g (3)
– (3 – h )2 + 2k = e 3-2 + k correct equation in k
EITHER
\(-(3- \frac{e+6}{2})^{2}+ 2k \) = e 3-2+ k
k = e+ \((\frac{6-e-6}{2})^{2}(-e+({\frac{-e}{2}})^2)\)
OR
k = e + \((3- \frac{e+6}{2})^2\)
k = e+ 9 -3e -18 + \(\frac{e^2+12e+36}{4}\)
THEN k= e + \(\frac{e^2}{4}\)
Question
A normal to the graph of \(y = \arctan (x – 1)\) , for \(x > 0\), has equation \(y = – 2x + c\) , where \(x \in \mathbb{R}\) .
Find the value of c.
▶️Answer/Explanation
Markscheme
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {\arctan (x – 1)} \right) = \frac{1}{{1 + {{(x – 1)}^2}}}\) (or equivalent) A1
\({m_N} = – 2{\text{ and so }}{m_T} = \frac{1}{2}\) (R1)
Attempting to solve \(\frac{1}{{1 + {{(x – 1)}^2}}} = \frac{1}{2}\) (or equivalent) for x M1
\(x = 2{\text{ (as }}x > 0)\) A1
Substituting \(x = 2\) and \(y = \frac{\pi }{4}\) to find c M1
\(c = 4 + \frac{\pi }{4}\) A1 N1
[6 marks]
Examiners report
There was a disappointing response to this question from a fair number of candidates. The differentiation was generally correctly performed, but it was then often equated to \( – 2x + c\) rather than the correct numerical value. A few candidates either didn’t simplify arctan(1) to \(\frac{\pi }{4}\), or stated it to be 45 or \(\frac{\pi }{2}\).
Question
Find the equation of the normal to the curve \(5x{y^2} – 2{x^2} = 18\) at the point (1, 2) .
▶️Answer/Explanation
Markscheme
\(5{y^2} + 10xy\frac{{{\text{d}}y}}{{{\text{d}}x}} – 4x = 0\) A1A1A1
Note: Award A1A1 for correct differentiation of \(5x{y^2}\).
A1 for correct differentiation of \( – 2{x^2}\) and 18.
At the point (1, 2), \(20 + 20\frac{{{\text{d}}y}}{{{\text{d}}x}} – 4 = 0\)
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{4}{5}\) (A1)
Gradient of normal \( = \frac{5}{4}\) A1
Equation of normal \(y – 2 = \frac{5}{4}(x – 1)\) M1
\(y = \frac{5}{4}x – \frac{5}{4} + \frac{8}{4}\)
\(y = \frac{5}{4}x + \frac{3}{4}\,\,\,\,\,(4y = 5x + 3)\) A1
[7 marks]
Examiners report
It was pleasing to see that a significant number of candidates understood that implicit differentiation was required and that they were able to make a reasonable attempt at this. A small number of candidates tried to make the equation explicit. This method will work, but most candidates who attempted this made either arithmetic or algebraic errors, which stopped them from gaining the correct answer.
Question
Consider the functions f and g defined by \(f(x) = {2^{\frac{1}{x}}}\) and \(g(x) = 4 – {2^{\frac{1}{x}}}\) , \(x \ne 0\) .
(a) Find the coordinates of P, the point of intersection of the graphs of f and g .
(b) Find the equation of the tangent to the graph of f at the point P.
▶️Answer/Explanation
Markscheme
(a) \({2^{\frac{1}{x}}} = 4 – {2^{\frac{1}{x}}}\)
attempt to solve the equation M1
x = 1 A1
so P is (1, 2) , as \(f(1) = 2\) A1 N1
(b) \(f'(x) = – \frac{1}{{{x^2}}}{2^{\frac{1}{x}}}\ln 2\) A1
attempt to substitute x-value found in part (a) into their \(f'(x)\) M1
\(f'(1) = – 2\ln 2\)
\(y – 2 = – 2\ln 2(x – 1)\,\,\,\,\,{\text{(or equivalent)}}\) M1A1 N0
[7 marks]
Examiners report
Most candidates answered part (a) correctly although some candidates showed difficulty solving the equation using valid methods. Part (b) was less successful with many candidates failing to apply chain rule to obtain the derivative of the exponential function.
Question
A tangent to the graph of \(y = \ln x\) passes through the origin.
(a) Sketch the graphs of \(y = \ln x\) and the tangent on the same set of axes, and hence find the equation of the tangent.
(b) Use your sketch to explain why \(\ln x \leqslant \frac{x}{{\text{e}}}\) for \(x > 0\) .
(c) Show that \({x^{\text{e}}} \leqslant {{\text{e}}^x}\) for \(x > 0\) .
(d) Determine which is larger, \({\pi ^{\text{e}}}\) or \({{\text{e}}^\pi }\) .
▶️Answer/Explanation
Markscheme
(a)
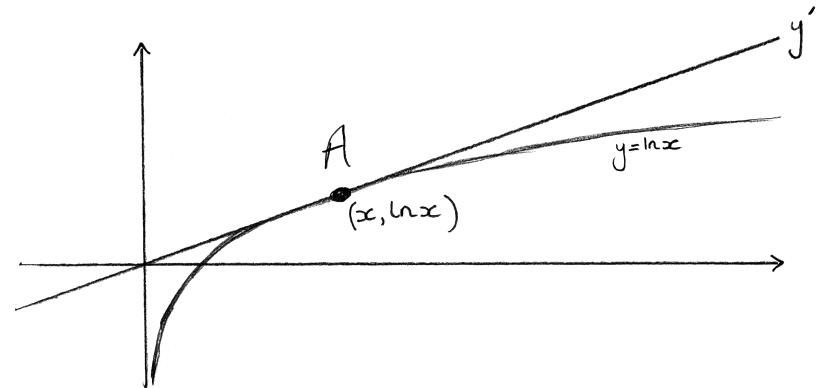 A3
A3
Note: Award A1 for each graph
A1 for the point of tangency.
point on curve and line is \((a,{\text{ }}\ln a)\) (M1)
\(y = \ln (x)\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x} \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{a}\,\,\,\,\,{\text{(when }}x = a)\) (M1)A1
EITHER
gradient of line, m, through (0, 0) and \((a,{\text{ }}\ln a)\) is \(\frac{{\ln a}}{a}\) (M1)A1
\( \Rightarrow \frac{{\ln a}}{a} = \frac{1}{a} \Rightarrow \ln a = 1 \Rightarrow a = {\text{e}} \Rightarrow m = \frac{1}{{\text{e}}}\) M1A1
OR
\(y – \ln a = \frac{1}{a}(x – a)\) (M1)A1
passes through 0 if
\(\ln a – 1 = 0\) M1
\(a = e \Rightarrow m = \frac{1}{{\text{e}}}\) A1
THEN
\(\therefore y = \frac{1}{{\text{e}}}x\) A1
[11 marks]
(b) the graph of \(\ln x\) never goes above the graph of \(y = \frac{1}{{\text{e}}}x\) , hence \(\ln x \leqslant \frac{x}{{\text{e}}}\) R1
[1 mark]
(c) \(\ln x \leqslant \frac{x}{{\text{e}}} \Rightarrow {\text{e}}\ln x \leqslant x \Rightarrow \ln {x^{\text{e}}} \leqslant x\) M1A1
exponentiate both sides of \(\ln {x^{\text{e}}} \leqslant x \Rightarrow {x^{\text{e}}} \leqslant {{\text{e}}^x}\) R1AG
[3 marks]
(d) equality holds when \(x = {\text{e}}\) R1
letting \(x = \pi \Rightarrow {\pi ^{\text{e}}} < {{\text{e}}^\pi }\) A1 N0
[2 marks]
Total [17 marks]
Examiners report
This was the least accessible question in the entire paper, with very few candidates achieving high marks. Sketches were generally done poorly, and candidates failed to label the point of intersection. A ‘dummy’ variable was seldom used in part (a), hence in most cases it was not possible to get more than 3 marks. There was a lot of good guesswork as to the coordinates of the point of intersection, but no reasoning showed. Many candidates started with the conclusion in part (c). In part (d) most candidates did not distinguish between the inequality and strict inequality.
Question
The normal to the curve \(x{{\text{e}}^{ – y}} + {{\text{e}}^y} = 1 + x\), at the point (c, \(\ln c\)), has a y-intercept \({c^2} + 1\).
Determine the value of c.
▶️Answer/Explanation
Markscheme
EITHER
differentiating implicitly:
\(1 \times {{\text{e}}^{ – y}} – x{{\text{e}}^{ – y}}\frac{{{\text{d}}y}}{{{\text{d}}x}} + {{\text{e}}^y}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) M1A1
at the point (c, \(\ln c\))
\(\frac{1}{c} – c \times \frac{1}{c}\frac{{{\text{d}}y}}{{{\text{d}}x}} + c\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) M1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{c}\,\,\,\,\,(c \ne 1)\) (A1)
OR
reasonable attempt to make expression explicit (M1)
\(x{{\text{e}}^{ – y}} + {{\text{e}}^y} = 1 + x\)
\(x + {{\text{e}}^{2y}} = {{\text{e}}^y}(1 + x)\)
\({{\text{e}}^{2y}} – {{\text{e}}^y}(1 + x) + x = 0\)
\(({{\text{e}}^y} – 1)({{\text{e}}^y} – x) = 0\) (A1)
\({{\text{e}}^y} = 1,{\text{ }}{{\text{e}}^y} = x\)
\(y = 0,{\text{ }}y = \ln x\) A1
Note: Do not penalize if y = 0 not stated.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x}\)
gradient of tangent \( = \frac{1}{c}\) A1
Note: If candidate starts with \(y = \ln x\) with no justification, award (M0)(A0)A1A1.
THEN
the equation of the normal is
\(y – \ln c = – c(x – c)\) M1
\(x = 0,{\text{ }}y = {c^2} + 1\)
\({c^2} + 1 – \ln c = {c^2}\) (A1)
\(\ln c = 1\)
\(c = {\text{e}}\) A1
[7 marks]
Examiners report
This was the first question to cause the majority of candidates a problem and only the better candidates gained full marks. Weaker candidates made errors in the implicit differentiation and those who were able to do this often were unable to simplify the expression they gained for the gradient of the normal in terms of c; a significant number of candidates did not know how to simplify the logarithms appropriately.
Question
Consider the curve \(y = x{{\text{e}}^x}\) and the line \(y = kx,{\text{ }}k \in \mathbb{R}\).
(a) Let k = 0.
(i) Show that the curve and the line intersect once.
(ii) Find the angle between the tangent to the curve and the line at the point of intersection.
(b) Let k =1. Show that the line is a tangent to the curve.
(c) (i) Find the values of k for which the curve \(y = x{{\text{e}}^x}\) and the line \(y = kx\) meet in two distinct points.
(ii) Write down the coordinates of the points of intersection.
(iii) Write down an integral representing the area of the region A enclosed by the curve and the line.
(iv) Hence, given that \(0 < k < 1\), show that \(A < 1\).
▶️Answer/Explanation
Markscheme
(a) (i) \(x{{\text{e}}^x} = 0 \Rightarrow x = 0\) A1
so, they intersect only once at (0, 0)
(ii) \(y’ = {{\text{e}}^x} + x{{\text{e}}^x} = (1 + x){{\text{e}}^x}\) M1A1
\(y'(0) = 1\) A1
\(\theta = \arctan 1 = \frac{\pi }{4}{\text{ }}(\theta = 45^\circ )\) A1
[5 marks]
(b) when \(k = 1,{\text{ }}y = x\)
\(x{{\text{e}}^x} = x \Rightarrow x({{\text{e}}^x} – 1) = 0\) M1
\( \Rightarrow x = 0\) A1
\(y'(0) = 1\) which equals the gradient of the line \(y = x\) R1
so, the line is tangent to the curve at origin AG
Note: Award full credit to candidates who note that the equation \(x({{\text{e}}^x} – 1) = 0\) has a double root x = 0 so y = x is a tangent.
[3 marks]
(c) (i) \(x{{\text{e}}^x} = kx \Rightarrow x({{\text{e}}^x} – k) = 0\) M1
\( \Rightarrow x = 0{\text{ or }}x = \ln k\) A1
\(k > 0{\text{ and }}k \ne 1\) A1
(ii) (0, 0) and \((\ln k,{\text{ }}k\ln k)\) A1A1
(iii) \(A = \left| {\int_0^{\ln k} {kx – x{{\text{e}}^x}{\text{d}}x} } \right|\) M1A1
Note: Do not penalize the omission of absolute value.
(iv) attempt at integration by parts to find \(\int {x{{\text{e}}^x}{\text{d}}x} \) M1
\(\int {x{{\text{e}}^x}{\text{d}}x} = x{{\text{e}}^x} – \int {{{\text{e}}^x}{\text{d}}x = {{\text{e}}^x}(x – 1)} \) A1
as \(0 < k < 1 \Rightarrow \ln k < 0\) R1
\(A = \int_{\ln k}^0 {kx – x{{\text{e}}^x}{\text{d}}x = \left[ {\frac{k}{2}{x^2} – (x – 1){{\text{e}}^x}} \right]_{\ln k}^0} \) A1
\( = 1 – \left( {\frac{k}{2}{{(\ln k)}^2} – (\ln k – 1)k} \right)\) A1
\( = 1 – \frac{k}{2}\left( {{{(\ln k)}^2} – 2\ln k + 2} \right)\)
\( = 1 – \frac{k}{2}\left( {{{(\ln k – 1)}^2} + 1} \right)\) M1A1
since \(\frac{k}{2}\left( {{{(\ln k – 1)}^2} + 1} \right) > 0\) R1
\(A < 1\) AG
[15 marks]
Total [23 marks]
Examiners report
Many candidates solved (a) and (b) correctly but in (c), many failed to realise that the equation \(x{{\text{e}}^x} = kx\) has two roots under certain conditions and that the point of the question was to identify those conditions. Most candidates made a reasonable attempt to write down the appropriate integral in (c)(iii) with the modulus signs and limits often omitted but no correct solution has yet been seen to (c)(iv).
Question
The curve C has equation \(y = \frac{1}{8}(9 + 8{x^2} – {x^4})\) .
a.Find the coordinates of the points on C at which \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) .[4]
b.The tangent to C at the point P(1, 2) cuts the x-axis at the point T. Determine the coordinates of T.[4]
c.The normal to C at the point P cuts the y-axis at the point N. Find the area of triangle PTN.[7]
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2x – \frac{1}{2}{x^3}\) A1
\(x\left( {2 – \frac{1}{2}{x^2}} \right) = 0\)
\(x = 0,{\text{ }} \pm 2\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) at \(\left( {0,\frac{9}{8}} \right),{\text{ }}\left( { – 2,\frac{{25}}{8}} \right),{\text{ }}\left( {2,\frac{{25}}{8}} \right)\) A1A1A1
Note: Award A2 for all three x-values correct with errors/omissions in y-values.
[4 marks]
at x =1, gradient of tangent \( = \frac{3}{2}\) (A1)
Note: In the following, allow FT on incorrect gradient.
equation of tangent is \(y – 2 = \frac{3}{2}(x – 1)\,\,\,\,\,\left( {y = \frac{3}{2}x + \frac{1}{2}} \right)\) (A1)
meets x-axis when y = 0 , \( – 2 = \frac{3}{2}(x – 1)\) (M1)
\(x = – \frac{1}{3}\)
coordinates of T are \(\left( { – \frac{1}{3},0} \right)\) A1
[4 marks]
gradient of normal \( = – \frac{2}{3}\) (A1)
equation of normal is \(y – 2 = – \frac{2}{3}(x – 1)\,\,\,\,\,\left( {y = – \frac{2}{3}x + \frac{8}{3}} \right)\) (M1)
at x = 0 , \(y = \frac{8}{3}\) A1
Note: In the following, allow FT on incorrect coordinates of T and N.
lengths of \({\text{PN}} = \sqrt {\frac{{13}}{9}} \) , \({\text{PT}} = \sqrt {\frac{{52}}{9}} \) A1A1
area of triangle \({\text{PTN}} = \frac{1}{2} \times \sqrt {\frac{{13}}{9}} \times \sqrt {\frac{{52}}{9}} \) M1
\( = \frac{{13}}{9}\) (or equivalent e.g. \(\frac{{\sqrt {676} }}{{18}}\)) A1
[7 marks]
Examiners report
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
Question
The curve C has equation \(y = \frac{1}{8}(9 + 8{x^2} – {x^4})\) .
Find the coordinates of the points on C at which \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) .
The tangent to C at the point P(1, 2) cuts the x-axis at the point T. Determine the coordinates of T.
The normal to C at the point P cuts the y-axis at the point N. Find the area of triangle PTN.
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2x – \frac{1}{2}{x^3}\) A1
\(x\left( {2 – \frac{1}{2}{x^2}} \right) = 0\)
\(x = 0,{\text{ }} \pm 2\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) at \(\left( {0,\frac{9}{8}} \right),{\text{ }}\left( { – 2,\frac{{25}}{8}} \right),{\text{ }}\left( {2,\frac{{25}}{8}} \right)\) A1A1A1
Note: Award A2 for all three x-values correct with errors/omissions in y-values.
[4 marks]
at x =1, gradient of tangent \( = \frac{3}{2}\) (A1)
Note: In the following, allow FT on incorrect gradient.
equation of tangent is \(y – 2 = \frac{3}{2}(x – 1)\,\,\,\,\,\left( {y = \frac{3}{2}x + \frac{1}{2}} \right)\) (A1)
meets x-axis when y = 0 , \( – 2 = \frac{3}{2}(x – 1)\) (M1)
\(x = – \frac{1}{3}\)
coordinates of T are \(\left( { – \frac{1}{3},0} \right)\) A1
[4 marks]
gradient of normal \( = – \frac{2}{3}\) (A1)
equation of normal is \(y – 2 = – \frac{2}{3}(x – 1)\,\,\,\,\,\left( {y = – \frac{2}{3}x + \frac{8}{3}} \right)\) (M1)
at x = 0 , \(y = \frac{8}{3}\) A1
Note: In the following, allow FT on incorrect coordinates of T and N.
lengths of \({\text{PN}} = \sqrt {\frac{{13}}{9}} \) , \({\text{PT}} = \sqrt {\frac{{52}}{9}} \) A1A1
area of triangle \({\text{PTN}} = \frac{1}{2} \times \sqrt {\frac{{13}}{9}} \times \sqrt {\frac{{52}}{9}} \) M1
\( = \frac{{13}}{9}\) (or equivalent e.g. \(\frac{{\sqrt {676} }}{{18}}\)) A1
[7 marks]
Examiners report
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
The whole of this question seemed to prove accessible to a high proportion of candidates.
(a) was well answered by most, although a number of candidates gave only the x-values of the points or omitted the value at 0.
(b) was successfully solved by the majority of candidates, who also found the correct equation of the normal in (c).
The last section proved more difficult for many candidates, the most common error being to use the wrong perpendicular sides. There were a number of different approaches here all of which were potentially correct but errors abounded.
Question
The curve C with equation \(y = f(x)\) satisfies the differential equation
\[\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{{\ln y}}(x + 2),{\text{ }}y > 1,\]
and y = e when x = 2.
Find the equation of the tangent to C at the point (2, e).
Find \(f(x)\).
Determine the largest possible domain of f.
Show that the equation \(f(x) = f'(x)\) has no solution.
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{\text{e}}}{{\ln {\text{e}}}}(2 + 2) = 4{\text{e}}\) A1
at (2, e) the tangent line is \(y – {\text{e}} = 4{\text{e}}(x – 2)\) M1
hence \(y = 4{\text{e}}x – 7{\text{e}}\) A1
[3 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{{\ln y}}(x + 2) \Rightarrow \frac{{\ln y}}{y}{\text{d}}y = (x + 2){\text{d}}x\) M1
\(\int {\frac{{\ln y}}{y}{\text{d}}y = \int {(x + 2){\text{d}}x} } \)
using substitution \(u = \ln y;{\text{ d}}u = \frac{1}{y}{\text{d}}y\) (M1)(A1)
\( \Rightarrow \int {\frac{{\ln y}}{y}{\text{d}}y = \int {u{\text{d}}u = \frac{1}{2}{u^2}} } \) (A1)
\( \Rightarrow \frac{{{{(\ln y)}^2}}}{2} = \frac{{{x^2}}}{2} + 2x + c\) A1A1
at (2, e), \(\frac{{{{(\ln {\text{e}})}^2}}}{2} = 6 + c\) M1
\( \Rightarrow c = – \frac{{11}}{2}\) A1
\( \Rightarrow \frac{{{{(\ln y)}^2}}}{2} = \frac{{{x^2}}}{2} + 2x – \frac{{11}}{2} \Rightarrow {(\ln y)^2} = {x^2} + 4x – 11\)
\(\ln y = \pm \sqrt {{x^2} + 4x – 11} \Rightarrow y = {{\text{e}}^{ \pm \sqrt {{x^2} + 4x – 11} }}\) M1A1
since y > 1, \(f(x) = {{\text{e}}^{\sqrt {{x^2} + 4x – 11} }}\) R1
Note:M1 for attempt to make y the subject.
[11 marks]
EITHER
\({x^2} + 4x – 11 > 0\) A1
using the quadratic formula M1
critical values are \(\frac{{ – 4 \pm \sqrt {60} }}{2}{\text{ }}\left( { = – 2 \pm \sqrt {15} } \right)\) A1
using a sign diagram or algebraic solution M1
\(x < – 2 – \sqrt {15} ;{\text{ }}x > – 2 + \sqrt {15} \) A1A1
OR
\({x^2} + 4x – 11 > 0\) A1
by methods of completing the square M1
\({(x + 2)^2} > 15\) A1
\( \Rightarrow x + 2 < – \sqrt {15} {\text{ or }}x + 2 > \sqrt {15} \) (M1)
\(x < – 2 – \sqrt {15} ;{\text{ }}x > – 2 + \sqrt {15} \) A1A1
[6 marks]
\(f(x) = f'(x) \Rightarrow f(x) = \frac{{f(x)}}{{\ln f(x)}}(x + 2)\) M1
\( \Rightarrow \ln \left( {f(x)} \right) = x + 2\,\,\,\,\,\left( { \Rightarrow x + 2 = \sqrt {{x^2} + 4x – 11} } \right)\) A1
\( \Rightarrow {(x + 2)^2} = {x^2} + 4x – 11 \Rightarrow {x^2} + 4x + 4 = {x^2} + 4x – 11\) A1
\( \Rightarrow 4 = – 11,{\text{ hence }}f(x) \ne f'(x)\) R1AG
[4 marks]
Examiners report
Nearly always correctly answered.
Most candidates separated the variables and attempted the integrals. Very few candidates made use of the condition y > 1, so losing 2 marks.
Part (c) was often well answered, sometimes with follow through.
Only the best candidates were successful on part (d).
Question
The curve C has equation \(2{x^2} + {y^2} = 18\). Determine the coordinates of the four points on C at which the normal passes through the point (1, 0) .
▶️Answer/Explanation
Markscheme
\(4x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = -\frac{{2x}}{y}\) M1A1
Note: Allow follow through on incorrect \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) from this point.
gradient of normal at (a, b) is \(\frac{b}{{2a}}\)
Note: No further A marks are available if a general point is not used
equation of normal at (a, b) is \(y – b = \frac{b}{{2a}}(x – a)\left( { \Rightarrow y = \frac{b}{{2a}}x + \frac{b}{2}} \right)\) M1A1
substituting (1, 0) M1
\(b = 0\) or \(a = -1\) A1A1
four points are \((3,{\text{ }}0),{\text{ }}( – 3,{\text{ 0}}),{\text{ }}( – 1,{\text{ }}4),{\text{ }}( – 1,{\text{ }} – 4)\) A1A1
Note: Award A1A0 for any two points correct.
[9 marks]
Examiners report
Many students were able to obtain the first marks in this question by implicit differentiation but few were able to complete the question successfully. There were a number of students obtaining the correct final answers, but could not be given the marks due to incorrect working. Most common was students giving the equation of the normal as \(y – 0 = \frac{y}{{2x}}(x – 1)\), instead of taking a general point e.g. (a, b)
Question
A curve is defined by the equation \(8y\ln x – 2{x^2} + 4{y^2} = 7\). Find the equation of the tangent to the curve at the point where x = 1 and \(y > 0\).
▶️Answer/Explanation
Markscheme
\(8y \times \frac{1}{x} + 8\frac{{{\text{d}}y}}{{{\text{d}}x}}\ln x – 4x + 8y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1A1
Note: M1 for attempt at implicit differentiation. A1 for differentiating \(8y\ln x\), A1 for differentiating the rest.
when \(x = 1,{\text{ }}8y \times 0 – 2 \times 1 + 4{y^2} = 7\) (M1)
\({y^2} = \frac{9}{4} \Rightarrow y = \frac{3}{2}{\text{ (as }}y > 0)\) A1
at \(\left( {1,\frac{3}{2}} \right)\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{2}{3}\) A1
\(y – \frac{3}{2} = – \frac{2}{3}(x – 1)\) or \(y = – \frac{2}{3}x + \frac{{13}}{6}\) A1
[7 marks]
Examiners report
The implicit differentiation was generally well done. Some candidates did not realise that they needed to substitute into the original equation to find \(y\). Others wasted a lot of time rearranging the derivative to make \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) the subject, rather than simply putting in the particular values for \(x\) and \(y\).
Question
The curve C is given by \(y = \frac{{x\cos x}}{{x + \cos x}}\), for \(x \geqslant 0\).
Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{{\cos }^2}x – {x^2}\sin x}}{{{{(x + \cos x)}^2}}},{\text{ }}x \geqslant 0\).
Find the equation of the tangent to C at the point \(\left( {\frac{\pi }{2},0} \right)\).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(x + \cos x)(\cos x – x\sin x) – x\cos x(1 – \sin x)}}{{{{(x + \cos x)}^2}}}\) M1A1A1
Note: Award M1 for attempt at differentiation of a quotient and a product condoning sign errors in the quotient formula and the trig differentiations, A1 for correct derivative of “u”, A1 for correct derivative of “v”.
\( = \frac{{x\cos x + {{\cos }^2}x – {x^2}\sin x – x\cos x\sin x – x\cos x + x\cos x\sin x}}{{{{(x + \cos x)}^2}}}\) A1
\( = \frac{{{{\cos }^2}x – {x^2}\sin x}}{{{{(x + \cos x)}^2}}}\) AG
[4 marks]
the derivative has value –1 (A1)
the equation of the tangent line is \((y – 0) = ( – 1)\left( {x – \frac{\pi }{2}} \right)\left( {y = \frac{\pi }{2} – x} \right)\) M1A1
[3 marks]
Examiners report
The majority of candidates earned significant marks on this question. The product rule and the quotient rule were usually correctly applied, but a few candidates made an error in differentiating the denominator, obtaining \( – \sin x\) rather than \(1 – \sin x\). A disappointing number of candidates failed to calculate the correct gradient at the specified point.
The majority of candidates earned significant marks on this question. The product rule and the quotient rule were usually correctly applied, but a few candidates made an error in differentiating the denominator, obtaining \( – \sin x\) rather than \(1 – \sin x\). A disappointing number of candidates failed to calculate the correct gradient at the specified point.
Question
Consider the function \(f(x) = \frac{{\ln x}}{x},{\text{ }}x > 0\).
The sketch below shows the graph of \(y = {\text{ }}f(x)\) and its tangent at a point A.

Show that \(f'(x) = \frac{{1 – \ln x}}{{{x^2}}}\).
Find the coordinates of B, at which the curve reaches its maximum value.
Find the coordinates of C, the point of inflexion on the curve.
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the equation of the tangent to the graph of \(f\) at the point A.
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the area enclosed by the curve \(y = f(x)\), the tangent at A, and the line \(x = {\text{e}}\).
▶️Answer/Explanation
Markscheme
\(f'(x) = \frac{{x \times \frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\) AG
[2 marks]
\(\frac{{1 – \ln x}}{{{x^2}}} = 0\) has solution \(x = {\text{e}}\) M1A1
\(y = \frac{1}{{\text{e}}}\) A1
hence maximum at the point \(\left( {{\text{e, }}\frac{1}{{\text{e}}}} \right)\)
[3 marks]
\(f”(x) = \frac{{{x^2}\left( { – \frac{1}{x}} \right) – 2x(1 – \ln x)}}{{{x^4}}}\) M1A1
\( = \frac{{2\ln x – 3}}{{{x^3}}}\)
Note: The M1A1 should be awarded if the correct working appears in part (b).
point of inflexion where \(f”(x) = 0\) M1
so \(x = {{\text{e}}^{\frac{3}{2}}},{\text{ }}y = \frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}\) A1A1
C has coordinates \(\left( {{{\text{e}}^{\frac{3}{2}}},{\text{ }}\frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}} \right)\)
[5 marks]
\(f(1) = 0\) A1
\(f'(1) = 1\) (A1)
\(y = x + c\) (M1)
through (1, 0)
equation is \(y = x – 1\) A1
[4 marks]
METHOD 1
area \( = \int_1^{\text{e}} {x – 1 – \frac{{\ln x}}{x}{\text{d}}x} \) M1A1A1
Note: Award M1 for integration of difference between line and curve, A1 for correct limits, A1 for correct expressions in either order.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}} ( + c)\) (M1)A1
\(\int {(x – 1){\text{d}}x = \frac{{{x^2}}}{2} – x( + c)} \) A1
\( = \left[ {\frac{1}{2}{x^2} – x – \frac{1}{2}{{(\ln x)}^2}} \right]_1^{\text{e}}\)
\( = \left( {\frac{1}{2}{{\text{e}}^2} – {\text{e}} – \frac{1}{2}} \right) – \left( {\frac{1}{2} – 1} \right)\)
\( = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
METHOD 2
area = area of triangle \( – \int_1^e {\frac{{\ln x}}{x}{\text{d}}x} \) M1A1
Note: A1 is for correct integral with limits and is dependent on the M1.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}( + c)} \) (M1)A1
area of triangle \( = \frac{1}{2}(e – 1)(e – 1)\) M1A1
\(\frac{1}{2}(e – 1)(e – 1) – \left( {\frac{1}{2}} \right) = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
[7 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The function \(f\) is defined as \(f(x) = {{\text{e}}^{3x + 1}},{\text{ }}x \in \mathbb{R}\).
(i) Find \({f^{ – 1}}(x)\).
(ii) State the domain of \({f^{ – 1}}\).
The function \(g\) is defined as \(g(x) = \ln x,{\text{ }}x \in {\mathbb{R}^ + }\).
The graph of \(y = g(x)\) and the graph of \(y = {f^{ – 1}}(x)\) intersect at the point \(P\).
Find the coordinates of \(P\).
The graph of \(y = g(x)\) intersects the \(x\)-axis at the point \(Q\).
Show that the equation of the tangent \(T\) to the graph of \(y = g(x)\) at the point \(Q\) is \(y = x – 1\).
A region \(R\) is bounded by the graphs of \(y = g(x)\), the tangent \(T\) and the line \(x = {\text{e}}\).
Find the area of the region \(R\).
A region \(R\) is bounded by the graphs of \(y = g(x)\), the tangent \(T\) and the line \(x = {\text{e}}\).
(i) Show that \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\).
(ii) By replacing \(x\) with \(\frac{1}{x}\) in part (e)(i), show that \(\frac{{x – 1}}{x} \le g(x),{\text{ }}x \in {\mathbb{R}^ + }\).
▶️Answer/Explanation
Markscheme
(i) \(x = {{\text{e}}^{3y + 1}}\) M1
Note: The M1 is for switching variables and can be awarded at any stage.
Further marks do not rely on this mark being awarded.
taking the natural logarithm of both sides and attempting to transpose M1
\(\left( {{f^{ – 1}}(x)} \right) = \frac{1}{3}(\ln x – 1)\) A1
(ii) \(x \in {\mathbb{R}^ + }\) or equivalent, for example \(x > 0\). A1
[4 marks]
\(\ln x = \frac{1}{3}(\ln x – 1) \Rightarrow \ln x – \frac{1}{3}\ln x = – \frac{1}{3}\) (or equivalent) M1A1
\(\ln x = – \frac{1}{2}\) (or equivalent) A1
\(x = {{\text{e}}^{ – \frac{1}{2}}}\) A1
coordinates of \(P\) are \(\left( {{{\text{e}}^{ – \frac{1}{2}}},{\text{ }} – \frac{1}{2}} \right)\) A1
[5 marks]
coordinates of \(Q\) are (\(1,{\rm{ }}0\)) seen anywhere A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{1}{x}\) M1
at \({\text{Q, }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1\) A1
\(y = x – 1\) AG
[3 marks]
let the required area be \(A\)
\(A = \int_1^e {x – 1{\text{d}}x – \int_1^e {\ln x{\text{d}}x} } \) M1
Note: The M1 is for a difference of integrals. Condone absence of limits here.
attempting to use integration by parts to find \(\int {\ln x{\text{d}}x} \) (M1)
\( = \left[ {\frac{{{x^2}}}{2} – x} \right]_1^{\text{e}} – [x\ln x – x]_1^{\text{e}}\) A1A1
Note: Award A1 for \(\frac{{{x^2}}}{2} – x\) and A1 for \(x\ln x – x\).
Note: The second M1 and second A1 are independent of the first M1 and the first A1.
\( = \frac{{{{\text{e}}^2}}}{2} – {\text{e}} – \frac{1}{2}\left( { = \frac{{{{\text{e}}^2} – 2{\text{e}} – 1}}{2}} \right)\) A1
[5 marks]
(i) METHOD 1
consider for example \(h(x) = x – 1 – \ln x\)
\(h(1) = 0\;\;\;{\text{and}}\;\;\;h'(x) = 1 – \frac{1}{x}\) (A1)
as \(h'(x) \ge 0\;\;\;{\text{for}}\;\;\;x \ge 1,\;\;\;{\text{then}}\;\;\;h(x) \ge 0\;\;\;{\text{for}}\;\;\;x \ge 1\) R1
as \(h'(x) \le 0\;\;\;{\text{for}}\;\;\;0 < x \le 1,\;\;\;{\text{then}}\;\;\;h(x) \ge 0\;\;\;{\text{for}}\;\;\;0 < x \le 1\) R1
so \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\) AG
METHOD 2
\(g”(x) = – \frac{1}{{{x^2}}}\) A1
\(g”(x) < 0\;\;\;\)(concave down) for\(\;\;\;x \in {\mathbb{R}^ + }\) R1
the graph of \(y = g(x)\) is below its tangent \((y = x – 1\;\;\;{\text{at}}\;\;\;x = 1)\) R1
so \(g(x) \le x – 1,{\text{ }}x \in {\mathbb{R}^ + }\) AG
Note: The reasoning may be supported by drawn graphical arguments.
METHOD 3
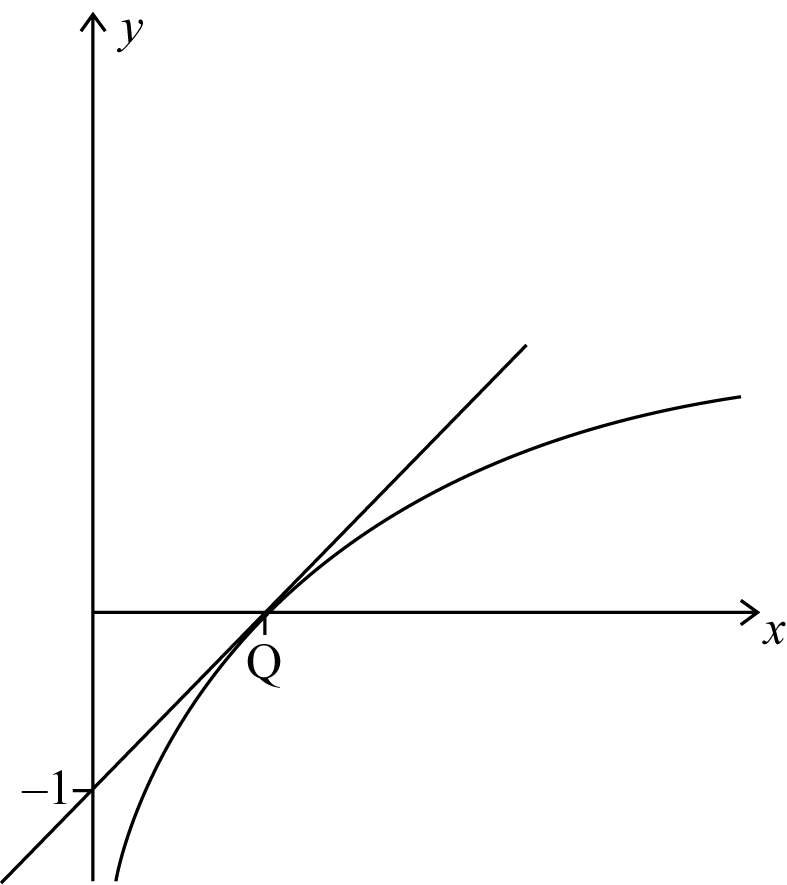
clear correct graphs of \(y = x – 1\;\;\;{\text{and}}\;\;\;\ln x\;\;\;{\text{for}}\;\;\;x > 0\) A1A1
statement to the effect that the graph of \(\ln x\) is below the graph of its tangent at \(x = 1\) R1AG
(ii) replacing \(x\) by \(\frac{1}{x}\) to obtain \(\ln \left( {\frac{1}{x}} \right) \le \frac{1}{x} – 1\left( { = \frac{{1 – x}}{x}} \right)\) M1
\( – \ln x \le \frac{1}{x} – 1\left( { = \frac{{1 – x}}{x}} \right)\) (A1)
\(\ln x \ge 1 – \frac{1}{x}\left( { = \frac{{x – 1}}{x}} \right)\) A1
so \(\frac{{x – 1}}{x} \le g(x),{\text{ }}x \in {\mathbb{R}^ + }\) AG
[6 marks]
Total [23 marks]
Examiners report
Generally very well done, even by candidates who had shown considerable weaknesses elsewhere on the paper.
Generally very well done, even by candidates who had shown considerable weaknesses elsewhere on the paper.
Generally very well done, even by candidates who had shown considerable weaknesses elsewhere on the paper.
A productive question for many candidates, but some didn’t realise that a difference of areas/integrals was required.
(i) Many candidates adopted a graphical approach, but sometimes with unconvincing reasoning.
(ii) Poorly answered. Many candidates applied the suggested substitution only to one side of the inequality, and then had to fudge the answer.
Question
Consider the curve \(y = \frac{1}{{1 – x}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 1\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Determine the equation of the normal to the curve at the point \(x = 3\) in the form \(ax + by + c = 0\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {(1 – x)^{ – 2}}\;\;\;\left( { = \frac{1}{{{{(1 – x)}^2}}}} \right)\) (M1)A1
[2 marks]
gradient of Tangent \( = \frac{1}{4}\) (A1)
gradient of Normal \( = – 4\) (M1)
\(y + \frac{1}{2} = – 4(x – 3)\) or attempt to find \(c\) in \(y = mx + c\) M1
\(8x + 2y – 23 = 0\) A1
[4 marks]
Total [6 marks]
Examiners report
[N/A]
[N/A]
Question
Find the \(x\)-coordinates of all the points on the curve \(y = 2{x^4} + 6{x^3} + \frac{7}{2}{x^2} – 5x + \frac{3}{2}\) at which
the tangent to the curve is parallel to the tangent at \(( – 1,{\text{ }}6)\).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 8{x^3} + 18{x^2} + 7x – 5\) A1
when \(x = – 1,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2\) A1
\(8{x^3} + 18{x^2} + 7x – 5 = – 2\) M1
\(8{x^3} + 18{x^2} + 7x – 3 = 0\)
\((x + 1)\) is a factor A1
\(8{x^3} + 18{x^2} + 7x – 3 = (x + 1)(8{x^2} + 10x – 3)\) (M1)
Note: M1 is for attempting to find the quadratic factor.
\((x + 1)(4x – 1)(2x + 3) = 0\)
\((x = – 1),{\text{ }}x = 0.25,{\text{ }}x = – 1.5\) (M1)A1
Note: M1 is for an attempt to solve their quadratic factor.
[7 marks]
Examiners report
The first half of the question was accessible to all the candidates. Some though saw the word ‘tangent’ and lost time calculating the equation of this. It was a pity that so many failed to spot that \(x + 1\) was a factor of the cubic and so did not make much progress with the final part of this question.
Question
A curve has equation \(3x – 2{y^2}{{\text{e}}^{x – 1}} = 2\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of \(x\) and \(y\).
Find the equations of the tangents to this curve at the points where the curve intersects the line \(x = 1\).
▶️Answer/Explanation
Markscheme
attempt to differentiate implicitly M1
\(3 – \left( {4y\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2{y^2}} \right){{\text{e}}^{x – 1}} = 0\) A1A1A1
Note: Award A1 for correctly differentiating each term.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 \bullet {{\text{e}}^{1 – x}} – 2{y^2}}}{{4y}}\) A1
Note: This final answer may be expressed in a number of different ways.
[5 marks]
\(3 – 2{y^2} = 2 \Rightarrow {y^2} = \frac{1}{2} \Rightarrow y = \pm \sqrt {\frac{1}{2}} \) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 – 2 \bullet \frac{1}{2}}}{{ \pm 4\sqrt {\frac{1}{2}} }} = \pm \frac{{\sqrt 2 }}{2}\) M1
at \(\left( {1,{\text{ }}\sqrt {\frac{1}{2}} } \right)\) the tangent is \(y – \sqrt {\frac{1}{2}} = \frac{{\sqrt 2 }}{2}(x – 1)\) and A1
at \(\left( {1,{\text{ }} – \sqrt {\frac{1}{2}} } \right)\) the tangent is \(y + \sqrt {\frac{1}{2}} = – \frac{{\sqrt 2 }}{2}(x – 1)\) A1
Note: These equations simplify to \(y = \pm \frac{{\sqrt 2 }}{2}x\).
Note: Award A0M1A1A0 if just the positive value of \(y\) is considered and just one tangent is found.
[4 marks]
Examiners report
[N/A]
[N/A]
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
a.Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).[2]
b.Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).[2]
c.Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).[2]
d.Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.[3]
e.Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
f.The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).[6]
g.Find the value of the curvature of the graph of \(f\) at the local maximum point.[3]
h.Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.[2]
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A
Note: Award M1A0 if extra zeros are seen.
[2 marks]
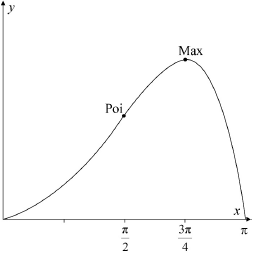
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).
Find \(\int {f(x)\cos x{\text{d}}x} \).
By finding \(g'(x)\) explain why \(g\) is an increasing function.
▶️Answer/Explanation
Markscheme
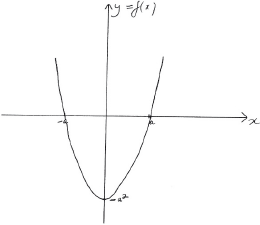
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
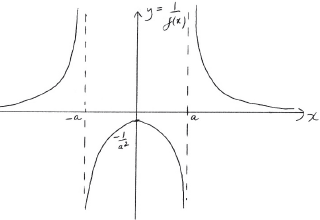
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
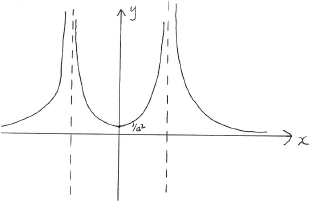
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the function \({f_n}(x) = (\cos 2x)(\cos 4x) \ldots (\cos {2^n}x),{\text{ }}n \in {\mathbb{Z}^ + }\).
Determine whether \({f_n}\) is an odd or even function, justifying your answer.
By using mathematical induction, prove that
\({f_n}(x) = \frac{{\sin {2^{n + 1}}x}}{{{2^n}\sin 2x}},{\text{ }}x \ne \frac{{m\pi }}{2}\) where \(m \in \mathbb{Z}\).
Hence or otherwise, find an expression for the derivative of \({f_n}(x)\) with respect to \(x\).
Show that, for \(n > 1\), the equation of the tangent to the curve \(y = {f_n}(x)\) at \(x = \frac{\pi }{4}\) is \(4x – 2y – \pi = 0\).
▶️Answer/Explanation
Markscheme
even function A1
since \(\cos kx = \cos ( – kx)\) and \({f_n}(x)\) is a product of even functions R1
OR
even function A1
since \((\cos 2x)(\cos 4x) \ldots = \left( {\cos ( – 2x)} \right)\left( {\cos ( – 4x)} \right) \ldots \) R1
Note: Do not award A0R1.
[2 marks]
consider the case \(n = 1\)
\(\frac{{\sin 4x}}{{2\sin 2x}} = \frac{{2\sin 2x\cos 2x}}{{2\sin 2x}} = \cos 2x\) M1
hence true for \(n = 1\) R1
assume true for \(n = k\), ie, \((\cos 2x)(\cos 4x) \ldots (\cos {2^k}x) = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\) M1
Note: Do not award M1 for “let \(n = k\)” or “assume \(n = k\)” or equivalent.
consider \(n = k + 1\):
\({f_{k + 1}}(x) = {f_k}(x)(\cos {2^{k + 1}}x)\) (M1)
\( = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\cos {2^{k + 1}}x\) A1
\( = \frac{{2\sin {2^{k + 1}}x\cos {2^{k + 1}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
\( = \frac{{\sin {2^{k + 2}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
so \(n = 1\) true and \(n = k\) true \( \Rightarrow n = k + 1\) true. Hence true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: To obtain the final R1, all the previous M marks must have been awarded.
[8 marks]
attempt to use \(f’ = \frac{{vu’ – uv’}}{{{v^2}}}\) (or correct product rule) M1
\({f’_n}(x) = \frac{{({2^n}\sin 2x)({2^{n + 1}}\cos {2^{n + 1}}x) – (\sin {2^{n + 1}}x)({2^{n + 1}}\cos 2x)}}{{{{({2^n}\sin 2x)}^2}}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
[3 marks]
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{\left( {{2^n}\sin \frac{\pi }{2}} \right)\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right) – \left( {\sin {2^{n + 1}}\frac{\pi }{4}} \right)\left( {{2^{n + 1}}\cos \frac{\pi }{2}} \right)}}{{{{\left( {{2^n}\sin \frac{\pi }{2}} \right)}^2}}}\) (M1)(A1)
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{({2^n})\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right)}}{{{{({2^n})}^2}}}\) (A1)
\( = 2\cos {2^{n + 1}}\frac{\pi }{4}{\text{ }}( = 2\cos {2^{n – 1}}\pi )\) A1
\({f’_n}\left( {\frac{\pi }{4}} \right) = 2\) A1
\({f_n}\left( {\frac{\pi }{4}} \right) = 0\) A1
Note: This A mark is independent from the previous marks.
\(y = 2\left( {x – \frac{\pi }{4}} \right)\) M1A1
\(4x – 2y – \pi = 0\) AG
[8 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
The line \(y=mx-25\) is tangent to the curve \(f(x)=x^{2}\). Find the possible values of \(m\).
METHOD A: Using derivatives (at the point of contact, \(f’=y’\) and \(f=y\)
▶️Answer/Explanation
Ans
\(f(x)=x^{2}, f'(x)=2x\), tangent line \(y=mx-25\)
At the point of contact:
\(f(x)=y \Rightarrow x^{2}=mx-25\) (1)
\(f'(x)=y’ \Rightarrow 2x=m\) (2)
We solve the system:
(1) and (2): \(x^{2}(2x)x-25\Leftrightarrow x^{2}=2x^{2}-25\Leftrightarrow x^{2}=25\Leftrightarrow x=\pm 5\)
From (2): If \(x=5, m=10, if x=-5, m=-10\)
METHOD B: In this case, we have a quadratic and a line which must have exactly one intersection point , \(\Delta =0\)).
Ans
\(f(x)=x^{2}\), line \(y = mx-25\)
\(f(x)=y \Leftrightarrow x^{2}= mx -25 \Leftrightarrow x^{2}-mx+25=0\)
The line is a tangent if \(\Delta =0\Leftrightarrow m^{2}-100=0\Leftrightarrow m=\pm 10\)
Question
The line \(y=mx-48\) is tangent to the curve \(y=x^{4}\).
(a) Find the possible values of \(m\).
(b) Hence find the equations of the possible tangent lines
▶️Answer/Explanation
Ans
(Only method A applies here!)
(a) \(y=x^{4}, \frac{\mathrm{d} y}{\mathrm{d} x}=4x^{3}\), tangent line \(y =mx-48\)
At the point of contact:
\(x^{4}= mx-48 (1)\)
\(4x^{3}=m (2)\)
We solve the system:
\((1) and (2): x^{4}=(4x^{3})x-48\Leftrightarrow x^{4}=4x^{4}-48\Leftrightarrow 3x^{4}=48\Leftrightarrow x^{4}=16\Leftrightarrow x=\pm 2\)
From (2): If \(x=2, m=32\), if \(x=-2, m=-32\)
(b) If \(m=32\) the tangent line is \(y = 32x-48\)
If \(m=-32\) the tangent line is \(y = -32x-48\)
Question
Let \(f(x)=5x^{2}+10\). Find the equation of the tangent line at point \(P(1,15)\).
▶️Answer/Explanation
Ans
Let \(f(x)=5x^{2}+10, f'(x)=10x\)
At \(P(1,15), m_{T}=10\), Tangent: \(y-15=10(x-1)\Rightarrow y=10x+5\)
Question
Let \(f(x)=5x^{2}+10\). Find the equations of the tangent lines passing through the point \(Q(1,10)\).
METHOD A: Express in terms of \(m\) the equation of a line of slope m passing through \(Q(1,10)\);
then use the fact that this line is tangent to the curve to find \(m\).
▶️Answer/Explanation
Ans
Let \(f(x)=5x^{2}+10\).
A line passing through Q(1,10) has the form \(y-10=m(x-1) \Rightarrow y=mx-m+10 \)
At the point of contact:
\(f(x)=y \Rightarrow 5x^{2}+10=mx-m+10 (1)\)
\(f'(x)=y’ \Rightarrow 10x=m (2)\)
We solve the system:
(1) and (2): \(5x^{2}+10=10x^{2}-10x+10\Leftrightarrow 5x^{2}-10x=0\Leftrightarrow 5x(x-2)=0\Leftrightarrow x=0 or x=2\)
From (2): If \(x=0, m=0\), if \(x=2, m=20\)
Therefore If \(m=0\) the tangent line is \(y=10\)
If \(m=20\) the tangent line is \(y=20x-10\)
METHOD B: Express in terms of \(a\) the equation of a tangent line at some point \(x = a\);
then use the fact that it passes though \(Q(1,10)\) to find \(a\).
Ans
\(f(x)=5x^{2}+10, f'(x)=10x\). At \(x=a, y=5a^{2}+10, m_{T}=10a\)
The tangent line is \(y-(5a^{2}+10)=10a(x-a)\Rightarrow y=5a^{2}-10=10ax-10a^{2}\)
\(\Rightarrow y=10ax-5a^{2}+10\)
The line passes through Q(1,10), so
\(10a-5a^{2}+10=10\Leftrightarrow 10a-5a^{2}=0\Leftrightarrow 5a(2-a)=0\Leftrightarrow a=0 or a=2\)
If \(a=0\) the tangent line is \(y=10\)
If \(a=2\) the tangent line is \(y=20x-10\)
Question
Consider the tangent to the curve \(y=x^{3}+4x^{2}+x-6\).
(a) Find the equation of this tangent at the point where \(x = –1\).
(b) Find the coordinates of the point where this tangent meets the curve again.
▶️Answer/Explanation
Ans
METHOD 1
(a) The equation of the tangent is \(y = –4x – 8\).
(b) The point where the tangent meets the curve again is (–2, 0).
METHOD 2
(a) \(y=-4\) and \(\frac{\mathrm{d} y}{\mathrm{d} x}=3x^{2}+8x+1=-4 at x=-1.\)
Therefore, the tangent equation is \(y= -4x-8\).
(b) This tangent meets the curve when \(-4x-8= x^{3}+4x^{2}+x-6\) which gives
\(x^{3}+4x^{2}+5x+2=0\Rightarrow (x+1)^{2}(x+2)=0\).
The required point of intersection is \((-2,0)\).
Question
Let \(f\) be the function defined for \(x>-\frac{1}{3}\) by \(f(x)=\ln (3x+1)\).
(a) Find \(f'(x)\).
(b) Find the equation of the normal to the curve \(y=f(x)\) at the point where \( x=2\)
Give your answer in the form \(y=ax+b\) where \( a,b\epsilon \mathbb {R}\)
▶️Answer/Explanation
Ans
(a) \(f'(x)=\frac{1}{3x+1}\times 3 \left (=\frac{3}{3x+1} \right )\)
(b) Hence when \(x=2\), gradient of tangent =\(\frac{3}{7}\)
\(\Rightarrow\) gradient of mormal is \(-\frac{7}{3}\)
\(y-\ln 7=-\frac{7}{3}(x-2)\)
\(y=-\frac{7}{3}x+\frac{14}{3}+\ln 7\)
(accept \(y=-2.33x+6.61\))
Question
The line \(y=16x-9\) is a tangent to the curve \(y=2x^{3}+ax^{2}+bx-9\) at the point (1,7). Find the values of \(a\) and \(b\).
▶️Answer/Explanation
Ans
For the curve, \(y=7\) when \(x=1 \Rightarrow x=1\Rightarrow a+b=14\), and
\(\frac{\mathrm{d} y}{\mathrm{d} x}=6x^{2}+2ax+b=16\) when \(x=1 \Rightarrow 2a+b=10\).
Solving gives \(a=-4\) and \(b=18\)
Question
The normal to the curve \(y=\frac{k}{x}+\ln x^{2}\), for \(x\neq 0, k\epsilon \mathbb {R}\) at the point where \(x =
2\), has equation \(3x+2y=b\) where \(b \epsilon R\). Find the exact value of \(k\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{k}{x^{2}}+\frac{2}{x}\) When \(x=2\), gradient of normal =\(-\frac{3}{2}\)
\(\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2}{3}\Rightarrow -\frac{k}{4}+1=\frac{2}{3}\Rightarrow k=\frac{4}{3}\)
Question
The normal to the curve \(y=\frac{k}{x}+\ln x^{2}\), for \(x\neq 0, k\epsilon \mathbb {R}\) at the point where \(x =
2\), has equation \(3x+2y=b\) where \(b \epsilon R\). Find the exact value of \(k\).
▶️Answer/Explanation
Ans
\(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{k}{x^{2}}+\frac{2}{x}\) When \(x=2\), gradient of normal =\(-\frac{3}{2}\)
\(\Rightarrow \frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2}{3}\Rightarrow -\frac{k}{4}+1=\frac{2}{3}\Rightarrow k=\frac{4}{3}\)
Question
Let \(f(x)=3x^{2}-x+4\). Find the values of \(m\) for which the line \(y=mx+1\) is a tangent to the graph of \(f\).
METHOD A: Using quadratics and Δ
▶️Answer/Explanation
Ans
Line and graph intersect when \(3x^{2}-x+4=mx+1\)
\(i.e 3x^{2}-(1+m)x+3=0\)
\(y=mx+1\) tangent to graph \(\Rightarrow\)
\(3x^{2}-(1+m)x+3=0\) has equal roots
i.e. \(b^{2}-4ac =0\)
\(\Rightarrow (1+m)^{2}-36=0\)
\(\Rightarrow m=5, m=-7\)
METHOD B: Using derivatives
Ans
\(f'(x)=6x-1\)
\(3x^{2}-x+4=mx+1\)
Substitute \(m= 6x-1\) into above
\(3x^{2}-6x^{2}+3=0\)
\(\Rightarrow x =\pm 1\)
\(\Rightarrow m=5, m =-7\)
Question
For what values of \(m\) is the line \(y=mx+5\) a tangent to the parabola \(y=4-x^{2}\)?
METHOD A: Using quadratics and Δ
▶️Answer/Explanation
Ans
\(y=4-x^{2} \frac{\mathrm{d} y}{\mathrm{d} x}= -2x= m\) when \(x= -\frac{m}{2}\)
Thus, \(\left (-\frac{m}{2},4-\frac{m^{2}}{4} \right )\) lies on \(y = mx+5\).
Then, \(4-\frac{m^{2}}{4}=-\frac{m^{2}}{2}+5\), so \(m^{2}=4\), so \(m= \pm 2\).
METHOD B: for intersection:
\(mx+5=4-x^{2} or x^{2}+mx+1=0\).
For tangency: discriminant = \(0\)
Thus, \(m^{2}-4=0\), so \(m\pm 2\)