Question: [Maximum mark: 8]
The continuous random variable X has probability density function
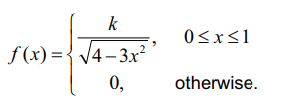
(a) Find the value of k .
(b) Find E(X) .
▶️Answer/Explanation
Ans:
(a) attempt to integrate \(\frac{k}{\sqrt{4-3x^{2}}}\)
\(= k \left \lfloor \frac{1}{\sqrt{3}}arcsin\left ( \frac{\sqrt{3}}{2}x \right ) \right \rfloor\)
Note: Award (M1)A0 for arcsin \(\left ( \frac{\sqrt{3}}{2}x \right )\)
Condone absence of k up to this stage.
equating their integrand to 1
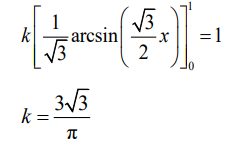
(b) \(E(X) = \frac{3\sqrt{3}}{\pi }\int_{0}^{1}\frac{x}{\sqrt{4-3x^{2}}}dx\)
Note: Condone absence of limits if seen at a later stage.
EITHER
attempt to integrate by inspection
\( = \frac{3\sqrt{3}}{\pi }\times -\frac{1}{6}\int -6x\left ( 4-3x^{2} \right )^{-\frac{1}{2}}dx\)
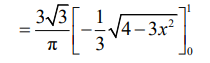
Note: Condone the use of k up to this stage.
OR
for example, \(u = 4-3c^{2} \Rightarrow \frac{du}{dx}= -6x\)
Note: Other substitutions may be used. For example, u = −3x2.
\(= – \frac{\sqrt{3}}{2\pi } \int_{4}^{1}u^{-\frac{1}{2}} du\)
Note: Condone absence of limits up to this stage.

Question
The function f is defined by
\[f(x) = \left\{ \begin{array}{r}1 – 2x,\\{\textstyle{3 \over 4}}{(x – 2)^2} – 3,\end{array} \right.\begin{array}{*{20}{c}}{x \le 2}\\{x > 2}\end{array}\]
a.Determine whether or not \(f\)is continuous.[2]
b.The graph of the function \(g\) is obtained by applying the following transformations to the graph of \(f\):
a reflection in the \(y\)–axis followed by a translation by the vector \(\left( \begin{array}{l}2\\0\end{array} \right)\).
Find \(g(x)\).[4]
▶️Answer/Explanation
Markscheme
\(1 – 2(2) = – 3\) and \(\frac{3}{4}{(2 – 2)^2} – 3 = – 3\) A1
both answers are the same, hence f is continuous (at \(x = 2\)) R1
Note: R1 may be awarded for justification using a graph or referring to limits. Do not award A0R1.
[2 marks]
reflection in the y-axis
\(f( – x) = \left\{ \begin{array}{r}1 + 2x,\\{\textstyle{3 \over 4}}{(x + 2)^2} – 3,\end{array} \right.\begin{array}{*{20}{c}}{x \ge – 2}\\{x < – 2}\end{array}\) (M1)
Note: Award M1 for evidence of reflecting a graph in y-axis.
translation \(\left( \begin{array}{l}2\\0\end{array} \right)\)
\(g(x) = \left\{ \begin{array}{r}2x – 3,\\{\textstyle{3 \over 4}}{x^2} – 3,\end{array} \right.\begin{array}{*{20}{c}}{x \ge 0}\\{x < 0}\end{array}\) (M1)A1A1
Note: Award (M1) for attempting to substitute \((x – 2)\) for x, or translating a graph along positive x-axis.
Award A1 for the correct domains (this mark can be awarded independent of the M1).
Award A1 for the correct expressions.
[4 marks]
Examiners report
[N/A]
[N/A]
Question
Find the \(x\)-coordinates of all the points on the curve \(y = 2{x^4} + 6{x^3} + \frac{7}{2}{x^2} – 5x + \frac{3}{2}\) at which
the tangent to the curve is parallel to the tangent at \(( – 1,{\text{ }}6)\).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 8{x^3} + 18{x^2} + 7x – 5\) A1
when \(x = – 1,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2\) A1
\(8{x^3} + 18{x^2} + 7x – 5 = – 2\) M1
\(8{x^3} + 18{x^2} + 7x – 3 = 0\)
\((x + 1)\) is a factor A1
\(8{x^3} + 18{x^2} + 7x – 3 = (x + 1)(8{x^2} + 10x – 3)\) (M1)
Note: M1 is for attempting to find the quadratic factor.
\((x + 1)(4x – 1)(2x + 3) = 0\)
\((x = – 1),{\text{ }}x = 0.25,{\text{ }}x = – 1.5\) (M1)A1
Note: M1 is for an attempt to solve their quadratic factor.
[7 marks]
Examiners report
The first half of the question was accessible to all the candidates. Some though saw the word ‘tangent’ and lost time calculating the equation of this. It was a pity that so many failed to spot that \(x + 1\) was a factor of the cubic and so did not make much progress with the final part of this question.
Question
The function \(f\) is defined as \(f(x) = a{x^2} + bx + c\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{R}\).
Hayley conjectures that \(\frac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}} = \frac{{f'({x_2}) + f'({x_1})}}{2},{\text{ }}x1 \ne x2\).
Show that Hayley’s conjecture is correct.
▶️Answer/Explanation
Markscheme
\(\frac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}} = \frac{{ax_2^2 + b{x_2} + c – (ax_1^2 + b{x_1} + c)}}{{{x_2} – {x_1}}}\) (M1)
\( = \frac{{a(x_2^2 – x_1^2) + b({x_2} – {x_1})}}{{{x_2} – {x_1}}}\) A1
\( = \frac{{a({x_2} – {x_1})({x_2} + {x_1}) + b({x_2} – {x_1})}}{{{x_2} – {x_1}}}\) (A1)
\( = a({x_2} + {x_1}) + b\,\,\,\,\,({x_1} \ne {x_2})\) A1
\(\frac{{f'({x_2}) + f'({x_1})}}{2} = \frac{{(2a{x_2} + b) + (2a{x_1} + b)}}{2}\) M1
\( = \frac{{2a({x_2} + {x_1}) + 2b}}{2}\)
\( = a({x_2} + {x_1}) + b\) A1
so Hayley’s conjecture is correct AG
[6 marks]
Examiners report
This was generally answered very well. A small minority attempted to ‘prove’ the result by substituting specific values into the identity and thus gained little or no credit. Some started by assuming the result to be correct, then manipulated both sides until they derived an obvious identity. Reluctantly, they gained credit for this, though such an approach should be discouraged.
Question
A curve has equation \(3x – 2{y^2}{{\text{e}}^{x – 1}} = 2\).
a.Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of \(x\) and \(y\).[5]
b.Find the equations of the tangents to this curve at the points where the curve intersects the line \(x = 1\).[4]
▶️Answer/Explanation
Markscheme
attempt to differentiate implicitly M1
\(3 – \left( {4y\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2{y^2}} \right){{\text{e}}^{x – 1}} = 0\) A1A1A1
Note: Award A1 for correctly differentiating each term.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 \bullet {{\text{e}}^{1 – x}} – 2{y^2}}}{{4y}}\) A1
Note: This final answer may be expressed in a number of different ways.
[5 marks]
\(3 – 2{y^2} = 2 \Rightarrow {y^2} = \frac{1}{2} \Rightarrow y = \pm \sqrt {\frac{1}{2}} \) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 – 2 \bullet \frac{1}{2}}}{{ \pm 4\sqrt {\frac{1}{2}} }} = \pm \frac{{\sqrt 2 }}{2}\) M1
at \(\left( {1,{\text{ }}\sqrt {\frac{1}{2}} } \right)\) the tangent is \(y – \sqrt {\frac{1}{2}} = \frac{{\sqrt 2 }}{2}(x – 1)\) and A1
at \(\left( {1,{\text{ }} – \sqrt {\frac{1}{2}} } \right)\) the tangent is \(y + \sqrt {\frac{1}{2}} = – \frac{{\sqrt 2 }}{2}(x – 1)\) A1
Note: These equations simplify to \(y = \pm \frac{{\sqrt 2 }}{2}x\).
Note: Award A0M1A1A0 if just the positive value of \(y\) is considered and just one tangent is found.
[4 marks]
Examiners report
[N/A]
[N/A]
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).
Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).
Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).
Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find the value of the curvature of the graph of \(f\) at the local maximum point.
Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
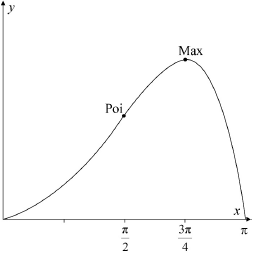
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
a.i.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);[2]
a.ii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);[4]
a.iii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).[2]
b.Find \(\int {f(x)\cos x{\text{d}}x} \).[5]
c.By finding \(g'(x)\) explain why \(g\) is an increasing function.[4]
▶️Answer/Explanation
Markscheme
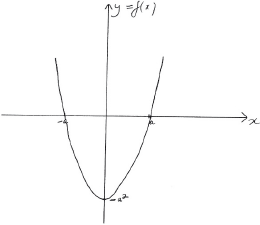
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
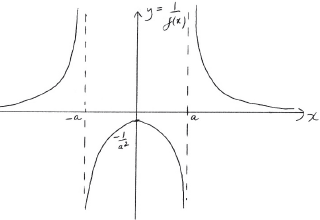
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
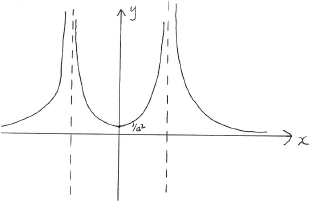
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the function \({f_n}(x) = (\cos 2x)(\cos 4x) \ldots (\cos {2^n}x),{\text{ }}n \in {\mathbb{Z}^ + }\).
a.Determine whether \({f_n}\) is an odd or even function, justifying your answer.[2]
b.By using mathematical induction, prove that \({f_n}(x) = \frac{{\sin {2^{n + 1}}x}}{{{2^n}\sin 2x}},{\text{ }}x \ne \frac{{m\pi }}{2}\) where \(m \in \mathbb{Z}\).[8]
c.Hence or otherwise, find an expression for the derivative of \({f_n}(x)\) with respect to \(x\).[3]
d.Show that, for \(n > 1\), the equation of the tangent to the curve \(y = {f_n}(x)\) at \(x = \frac{\pi }{4}\) is \(4x – 2y – \pi = 0\).[8]
▶️Answer/Explanation
Markscheme
even function A1
since \(\cos kx = \cos ( – kx)\) and \({f_n}(x)\) is a product of even functions R1
OR
even function A1
since \((\cos 2x)(\cos 4x) \ldots = \left( {\cos ( – 2x)} \right)\left( {\cos ( – 4x)} \right) \ldots \) R1
Note: Do not award A0R1.
[2 marks]
consider the case \(n = 1\)
\(\frac{{\sin 4x}}{{2\sin 2x}} = \frac{{2\sin 2x\cos 2x}}{{2\sin 2x}} = \cos 2x\) M1
hence true for \(n = 1\) R1
assume true for \(n = k\), ie, \((\cos 2x)(\cos 4x) \ldots (\cos {2^k}x) = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\) M1
Note: Do not award M1 for “let \(n = k\)” or “assume \(n = k\)” or equivalent.
consider \(n = k + 1\):
\({f_{k + 1}}(x) = {f_k}(x)(\cos {2^{k + 1}}x)\) (M1)
\( = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\cos {2^{k + 1}}x\) A1
\( = \frac{{2\sin {2^{k + 1}}x\cos {2^{k + 1}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
\( = \frac{{\sin {2^{k + 2}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
so \(n = 1\) true and \(n = k\) true \( \Rightarrow n = k + 1\) true. Hence true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: To obtain the final R1, all the previous M marks must have been awarded.
[8 marks]
attempt to use \(f’ = \frac{{vu’ – uv’}}{{{v^2}}}\) (or correct product rule) M1
\({f’_n}(x) = \frac{{({2^n}\sin 2x)({2^{n + 1}}\cos {2^{n + 1}}x) – (\sin {2^{n + 1}}x)({2^{n + 1}}\cos 2x)}}{{{{({2^n}\sin 2x)}^2}}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
[3 marks]
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{\left( {{2^n}\sin \frac{\pi }{2}} \right)\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right) – \left( {\sin {2^{n + 1}}\frac{\pi }{4}} \right)\left( {{2^{n + 1}}\cos \frac{\pi }{2}} \right)}}{{{{\left( {{2^n}\sin \frac{\pi }{2}} \right)}^2}}}\) (M1)(A1)
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{({2^n})\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right)}}{{{{({2^n})}^2}}}\) (A1)
\( = 2\cos {2^{n + 1}}\frac{\pi }{4}{\text{ }}( = 2\cos {2^{n – 1}}\pi )\) A1
\({f’_n}\left( {\frac{\pi }{4}} \right) = 2\) A1
\({f_n}\left( {\frac{\pi }{4}} \right) = 0\) A1
Note: This A mark is independent from the previous marks.
\(y = 2\left( {x – \frac{\pi }{4}} \right)\) M1A1
\(4x – 2y – \pi = 0\) AG
[8 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
The graph of the function \(f\) is shown below
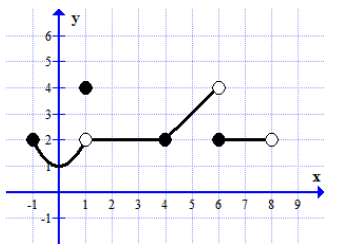
- Write down the domain and the range of the function.
Domain of \(f\) : Range of \(f \): - Complete the following table of values
\(f (-1)=\) \(f (1)=\) \(f (4)=\) \(f (6)=\) \(f (8)=\) - Complete the following table of limits (if there exist)
\(\lim_{x\rightarrow 1^{-}}f(x)=\) \(\lim_{x\rightarrow 1^{+}}f(x)=\) \(\lim_{x\rightarrow 1}f(x)=\) \(\lim_{x\rightarrow 4^{-}}f(x)=\) \(\lim_{x\rightarrow 4^{+}}f(x)=\) \(\lim_{x\rightarrow 4}f(x)=\) \(\lim_{x\rightarrow 6^{-}}f(x)=\) \(\lim_{x\rightarrow 6^{+}}f(x)=\) \(\lim_{x\rightarrow 6}f(x)=\) - Determine whether the functions is continuous at \(x = 4 , x =1, x= 6\) .
Is \(f\) continuous at \(x = 4\) YES, since \(\lim_{x\rightarrow 4}f(x)=2\) and \(f(4)=2\) Is \(f\) continuous at \(x = 1\) Is \(f\) continuous at \(x = 6\)
▶️Answer/Explanation
Ans:
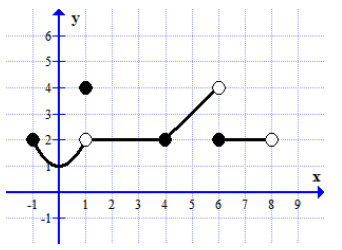
Domain of \(f\) : \(x \in [-1,8]\)
Range of \(f \): \(y \in [1,4]\) \(f (-1)=2\) \(f (1)=4\) \(f (4)=2\) \(f (6)=2\) \(f (8)=\) not defined - Complete the following table of limits (if there exist)
\(\lim_{x\rightarrow 1^{-}}f(x)=2\) \(\lim_{x\rightarrow 1^{+}}f(x)=2\) \(\lim_{x\rightarrow 1}f(x)=2\) \(\lim_{x\rightarrow 4^{-}}f(x)=2\) \(\lim_{x\rightarrow 4^{+}}f(x)=2\) \(\lim_{x\rightarrow 4}f(x)=2\) \(\lim_{x\rightarrow 6^{-}}f(x)=4\) \(\lim_{x\rightarrow 6^{+}}f(x)=2\) \(\lim_{x\rightarrow 6}f(x)\) does not exist. - Determine whether the functions is continuous at \(x = 4 , x =1, x= 6\) .
Is \(f\) continuous at \(x = 4\) YES, since \(\lim_{x\rightarrow 4}f(x)=2\) and \(f(4)=2\) Is \(f\) continuous at \(x = 1\) NO, since \(\lim_{x\rightarrow 1}f(x)=2\) and \(f(1)=4 \space 2 \ne 4.\) Is \(f\) continuous at \(x = 6\) NO, since \(\lim_{x\rightarrow 6}f(x)\) does not exist.
Question
Let
\(f(x)=\left\{\begin{matrix} x^2+1 & -1 \le x < 1 \\ 4 & x=1 \\ 2 & 1< x \le 4 \\ x-2 & 4 < x < 6 \\ 2 & 6 \le x < 8 \end{matrix}\right.\)
Domain of \(f\) : - Complete the following table of values
\(f (-1)=\) \(f (1)=\) \(f (4)=\) \(f (6)=\) \(f (8)=\) - Complete the following table of limits (if there exist)
\(\lim_{x\rightarrow 1^{-}}f(x)=\lim_{x\rightarrow 1^{-}}(x^2+1)=2\) \(\lim_{x\rightarrow 1^{+}}f(x)=\) \(\lim_{x\rightarrow 1}f(x)=\) \(\lim_{x\rightarrow 4^{-}}f(x)=\) \(\lim_{x\rightarrow 4^{+}}f(x)=\) \(\lim_{x\rightarrow 4}f(x)=2\) \(\lim_{x\rightarrow 6^{-}}f(x)=\) \(\lim_{x\rightarrow 6^{+}}f(x)=\) \(\lim_{x\rightarrow 6}f(x)=\) - Determine whether the functions is continuous at \(x = 4 , x =1, x= 6\) .
Is \(f\) continuous at \(x = 4\) Is \(f\) continuous at \(x = 1\) Is \(f\) continuous at \(x = 6\)
▶️Answer/Explanation
Ans: In fact, it is the same function as in exercise 1.
\(f(x)=\left\{\begin{matrix} x^2+1 & -1 \le x < 1 \\ 4 & x=1 \\ 2 & 1< x \le 4 \\ x-2 & 4 < x < 6 \\ 2 & 6 \le x < 8 \end{matrix}\right.\)
(a) and (b) as in exercise 1
c.
| \(\lim_{x\rightarrow 1^{-}}f(x)=\lim_{x\rightarrow 1^{-}}(x^2+1)=2\) |
| \(\lim_{x\rightarrow 1^{+}}f(x)=\lim_{x\rightarrow 1^{+}}2=2\) |
| \(\lim_{x\rightarrow 1}f(x)=2\) |
| \(\lim_{x\rightarrow 4^{-}}f(x)=\lim_{x\rightarrow 4^{-}}2=2\) |
| \(\lim_{x\rightarrow 4^{+}}f(x)=\lim_{x\rightarrow 4^{+}}(x-2)=2\) |
| \(\lim_{x\rightarrow 4}f(x)=2\) |
| \(\lim_{x\rightarrow 6^{-}}f(x)=\lim_{x\rightarrow 6^{-}}(x-2)=4\) |
| \(\lim_{x\rightarrow 6^{+}}f(x)=\lim_{x\rightarrow 6^{+}}2=2\) |
| \(\lim_{x\to 6}f(x)\) does not exist. |
d. as in exercise 1
Question
- Write down the values of the following limits
\(\lim_{x\to 3} \frac{x+3}{x-2}=\) \(\lim_{x\to +\infty} \frac{x+3}{x-2}=\) \(\lim_{x\to -\infty} \frac{x+3}{x-2}=\) - Investigate whether each of the following side limits is \(+\infty\) or \(-\infty\)
\(\lim_{x\to 2^{+}} \frac{x+3}{x-2}=\) \(\lim_{x\to 2^{-}} \frac{x+3}{x-2}=\) \(\lim_{x\to 2^{+}} \frac{x-3}{x-2}=\) \(\lim_{x\to 2^{-}} \frac{x-3}{x-2}=\)
▶️Answer/Explanation
Ans:
\(\lim_{x\to 3} \frac{x+3}{x-2}=6\) \(\lim_{x\to +\infty} \frac{x+3}{x-2}=1\) \(\lim_{x\to -\infty} \frac{x+3}{x-2}=-1\) \(\lim_{x\to 2^{+}} \frac{x+3}{x-2}=+\infty\) \(\lim_{x\to 2^{-}} \frac{x+3}{x-2}=-\infty\) \(\lim_{x\to 2^{+}} \frac{x-3}{x-2}=-\infty\) \(\lim_{x\to 2^{-}} \frac{x-3}{x-2}=+\infty\)
Question
- Sketch the graphs of the functions \(f(x)=x+3\) and \(g(x)=\frac{x^2-9}{x-3}\).
- Find \(\lim_{x\to 3} f(x)\) and \(\lim_{x\to 3} g(x)\)
- Explain the difference between the two functions
▶️Answer/Explanation
Ans:
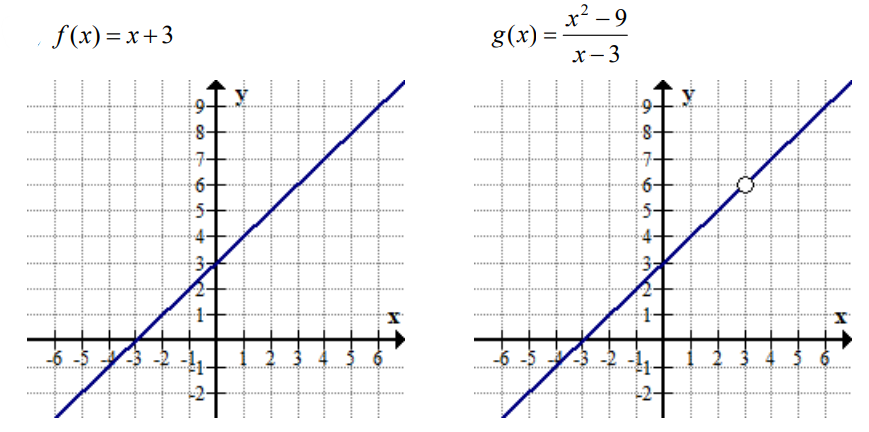
- \(\lim_{x\to 3} f(x)=6\) and \(\lim_{x\to 3}g(x)=6\)
- The graphs coincide except the point at \(x = 3\) where \(g(x)\) is not defined.
Question
Show by using first principles that
- The derivative of \(f(x)=x^4\) is \(f'(x)=4x^3\)
- The derivative of \(f(x)=x^3+2x_1\) is \(f'(x)=3x^2+2\)
▶️Answer/Explanation
Ans:
- for \(f(x)=x^4\)
\(f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} = \lim_{h\to 0} \frac{(x+h)^4-x^4}{h}\)
\(=\lim_{h\to 0}\frac{x^4+4x^3h+6x^2h^2+4xh^3+h^4-x^4}{h}\)
\(=\lim_{h\to 0}\frac{4x^3h+6x^2h^2+4xh^3+h^4}{h}\)
\(=\lim_{h\to 0}\frac{h(4x^3+6x^2h+4xh^2+h^3)}{h}\)
\(=\lim_{h\to 0}(4x^3+6x^2h+4xh^2+h^3)\)
\(=4x^3\) - for \(f(x)=x^3+2x+1\)
\(f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} = \lim_{h\to 0} \frac{(x+h)^3+2(x+h)+1-x^3-2x-1}{h}\)
\(=\lim_{h\to 0}\frac{x^3+3x^2h+3xh^2+h^3+2x+2h-x^3-2x}{h}\)
\(=\lim_{h\to 0}\frac{3x^2h+3xh^2+h^3+2h}{h}\)
\(=\lim_{h\to 0}\frac{h(3x^2+3xh+h^2+2)}{h}\)
\(=\lim_{h\to 0}(3x^2+3xh+h^2+2)\)
\(=3x^2+2\)
Question
Let \(f(x)=(2x+3)^2\)
- Find \(f'(x)\) by using the chain rule and then \(f'(2)\)
- Confirm the results in (a) by using the definition of the derivative as follows
- \(f'(x)=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h}\)
- \(f'(2)=\lim_{h\to 0} \frac{f(2+h)-f(2)}{h}\)
- Find \(f'(0)\) from first principles.
▶️Answer/Explanation
Ans:
- \(f(x)=(2x+3)^2\)
\(f'(x)=2(2x+3)×2=8x+12\) and \(f'(2)=28\) - \(f'(x)= \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{(2(x+h)+3)^2-(2x+3)^2}{h}\)
\(=\lim_{h\to 0} \frac{4(x+h)^2+12(x+h)+9-4x^2-12x-9}{h}\)
\(=\lim_{h\to 0}\frac{4(x^2+2xh+h^2)+12x+12h-4x^2-12x}{h}\)
\(=\lim_{h\to 0}\frac{8xh+4h^2+12h}{h}\)
\(=\lim_{h\to 0}(8x+4h+12)\)
\(8x+12\) - \(f'(2)=\lim_{h\to 0}\frac{f(2+h)-f(2)}{h}=\lim_{h\to 0}\frac{(2(2+h)+3)^2-49}{h}\)
\(=\lim_{h\to 0} \frac{(2h+7)^2-49}{h}\)
\(=\lim_{h\to 0} \frac{4h^2+28h+49-49}{h}\)
\(=\lim_{h\to 0} \frac{4h^2+28h}{h}= \lim_{h\to 0}(4h+28)=28\)
- \(f'(x)= \lim_{h\to 0} \frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{(2(x+h)+3)^2-(2x+3)^2}{h}\)
- \(f'(0)=\lim_{h\to 0}\frac{f(0+h)-f(0)}{h}=\lim_{h\to 0} \frac{f(h)-f(0)}{h}\)
\(=\lim_{h\to 0} \frac{(2h+3)^2-9}{h}\)
\(=\lim_{h\to 0} \frac{4h^2+12h+9-9}{h}\)
\(=\lim_{h\to 0} \frac{4h^2+12h}{h}=\lim_{h\to 0} (4h+12)=12\)
Question
Find the derivatives of the following functions from first principles
- \(f(x)=mx+c\)
- \(f(x)=\sqrt{x}\)
- \(f(x)=\frac{1}{x^2}\)
▶️Answer/Explanation
Ans:
- for \(f(x)=mx+c\)
\(f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{m(x+h)+c-mx-c}{h}=\lim_{h\to 0}\frac{mh}{m}=\lim_{h\to 0}m=m\) - for \(f(x)=\sqrt{x}\)
\(f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}=\lim_{h\to 0}\frac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}\)
\(=\lim_{h\to 0}\frac{1}{\sqrt{x+h}+\sqrt{x}}=\frac{1}{2\sqrt{x}}\) - for \(f(x)=\frac{1}{x^2}\)
\(f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}\frac{1}{h}\left (\frac{1}{(x+h)^2}-\frac{1}{x^2} \right )=\lim_{h\to 0}\frac{1}{h}\left ( \frac{x^2-(x+h)^2}{x^2(x+h)^2} \right )\)
\(=\lim_{h\to 0} \frac{-2xh-h^2}{hx^2(x+h)^2}=\lim_{h\to 0} \frac{-2x-h}{x^2(x+h)^2}=-\frac{2x}{x^4}=-\frac{2}{x^3}\)
Question
Let
\(f(x)=\left\{\begin{matrix} x+2 & x \le 1 \\ 4 & 1<x\le 3 \\-2x+10 & x>3 \end{matrix}\right. \)
- Sketch the graph of \(f\) on the diagram below.
- Explain why \(f\) is neither continuous nor differentiable at \(x=1\).
- Explain why \(f\) is continuous but not differentiable at \(x=3\).
▶️Answer/Explanation
Ans:
b. \(\lim_{x\to 1^{-}}f(x)=3, \lim_{x\to 1^{+}}f(x)=4\)⇒ limit does not exist. Not continuous so not differentiable.
c. at \(x=3 \lim_{x\to 3^{-}}f(x)=\lim_{x\to 3^{+}}f(x)=f(3)=4\) so continuous
Not differentiable at \(x=3\) since the gradient changes from 0 to -2
Question
Consider the continuous function
\(f(x)=\left\{\begin{matrix} x+a & x < 2 \\ 2a & x=2 \\bx+8 & x>2 \end{matrix}\right. \)
- Find the value of \(a\).
- Find the value of \(b\).
- Sketch the graph of \(f\) on the diagram below.
- Explain why the function is not differentiable at \(x=2\)
▶️Answer/Explanation
Ans:
a. \(a=2\)
b. \(b=-2\)
d. gradient changes from 1 to -2 at \(x = 2\)
Question
Let
\(f(x)=\left\{\begin{matrix} x^2+2 & x \le 0 \\ 2 & 0<x\le 3 \\x-1 & x>3 \end{matrix}\right. \)
- Sketch the graph of \(f\) on the diagram below.
- Show that \(f\) is continuous.
- Explain why \(f\) is differentiable at \(x=0\)
- Write down the equation of the tangent line at \(x=0\)
- Explain why \(f\) is not differentiable at \(x=3\)
▶️Answer/Explanation
Ans:
b. at \(x=0 \lim_{x\to 0^{-}}f(x)=f(0)=2\)
at \(x=3 \lim_{x\to 3^{-}}f(x)=f(3)=2\)
c. gradient does not change at \(x = 0\) . It is \(0\)
d. \(y=2\)
e. gradient changes from 0 to 1 at \(x = 3\).
Question
Let
\(f(x)=\left\{\begin{matrix} x^2-4x+3 & x<3 \\ c & x=3 \\ax+b & x>3 \end{matrix}\right. \)
- Given that the function is continuous
- Find the value of \(c\).
- Find a linear relation for \(a\) and \(b\).
- Given that the function is differentiable, find the values of \(a\) and \(b\).
- For \(a=2,b=-6\) and \(c=2\)
- Sketch the graph of \(f\) on the diagram below.
- Find, if there exist, \(\lim_{x\to 3}f(x)\) and \(f'(3)\)

▶️Answer/Explanation
Ans:
a.
- \(c=0\)
- \(3a+b=0\)
- gradient before \(x=3\) is 2, gradient after \(x=3\) is \(a\), so \(a = 2\). So \(b=-6\)
- \(\lim_{x\to 3}f(x)=0,f'(3)\) does not exist, (at 3, not continuous ⇒ not differentiable)
Question
Let \(f(x)=\left\{\begin{matrix} -2x^3 & x<1 \\x^2+ax+b & x\ge 1 \end{matrix}\right. \)
The function is continuous and differentiable.
- Find the values of \(a\) and of \(b\).
- Find the range of \(f (x)\)
- Find the equation of the tangent line to the curve \(y = f (x)\) at \(x = 1\) .
▶️Answer/Explanation
Ans:
- \(-2=1+a+b⇒a+b=-3\)
Gradient before \(x=1:-6x^2,\) gradient after \(x=1:2x+a,\) so \(-6=2+a\)⇒\(a=-8\)
Thus \(b=5\) - \(y \ge -11\)
- \(m=-6,\) point \((1,-2)\). Tangent line: \(y+2=-6(x-1)\)