Question
Consider the function f ( x ) = ax3 + bx2 + cx + d, where x ∈ R and a, b, c , d ∈ R.
(i) Write down an expression for f ′( x ).
(ii) Hence, given that f –1 does not exist, show that b2 – 3ac > 0 . [4]
Consider the function g ( x ) \(\frac{1}{2}\) x3 – 3x2 + 6x – 8 , where x ∈ R.
Show that g–1 exists.
g ( x ) can be written in the form p ( x – 2 )3 + q , where p , q ∈ R. Find the value of p and the value of q .
Hence find g–1 ( x ). [8]
The graph of y = g ( x ) may be obtained by transforming the graph of y = x3 using a sequence of three transformations.
State each of the transformations in the order in which they are applied. [3]
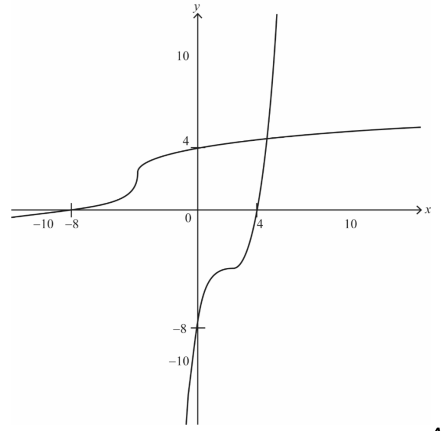
Sketch the graphs of y = g ( x ) and y = g–1 ( x ) on the same set of axes, indicating the points where each graph crosses the coordinate axes. [5]
▶️Answer/Explanation
Ans:
- (a) (i) f'(x)=\(3ax^{2}\)+2bx+c
- (a) (ii)
- \(since f^{-1}\)dose not exist , there must be two turning points
- (f(x)= 0)has more than one solutin
- using the disriminat Δ >0
- \(4b^{2}-12ac>0\)
- \(b^{2}\)-3ac>0
- (b) (i)
- METHOD 1
- \(b^{2}-3ac=(-3)^{2}-3\times \frac{1}{2}\times 6\) = 9-9 = 0
- hence g-1 exists
- METHOD 2
- g'(x)= \(\frac{3}{2}x^{2}-6x+6\)
- \(\Delta = (-6)^{2}-4\times \frac{3}{2}\times 6\)
- Δ = 36 -36 = 0 ⇒ there is (only) one point with gradient of 0 and this must be a point of inflexion (since g (x ) is a cubic.)
hence g-1 exists
- (b) (ii)
- p= \(\frac{1}{2}\)
- \((x-2)^{3}=x^{3}-6x^{2}\)+12x=8
- \(\frac{1}{2}(x^{3}-6x^{3}+12x-8)\)= \(\frac{1}{2}x^{3}-3x^{2}+6x-4\)
- g(x)=\(\frac{1}{2}(x-2)^{3}-4\)
- (b) (iii)
- x= \(\frac{1}{2}(y-2)^{3}-4\)
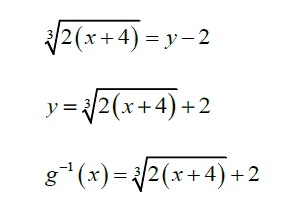
- (c)
- translation through \(\begin{pmatrix}
2\\
0
\end{pmatrix}\) - EITHER
- a stretch scale factor \(\frac{1}{2}\) parallel to the y-axis then a translation through \((_{-4}^{0})\)
- OR
- a translation through \((_{-8}^{0})\) then a stretch scale factor \(\frac{1}{2}\) parallel to the y-axis
- translation through \(\begin{pmatrix}
- (d)
Question
The acceleration, a ms-2 , of a particle moving in a horizontal line at time t seconds, t ≥ 0 , is given by a = – (1+v) where v ms-1 is the particle’s velocity and v > -1.
At t = 0 , the particle is at a fixed origin O and has initial velocity v0 ms-1 .
(a) By solving an appropriate differential equation, show that the particle’s velocity at time t is given by v ( t ) = (1 + v0) e-t – 1 . [6]
(b) Initially at O, the particle moves in the positive direction until it reaches its maximum displacement from O. The particle then returns to O.
Let s metres represent the particle’s displacement from O and smax its maximum displacement from O.
(i) Show that the time T taken for the particle to reach smax satisfies the equation eT = 1 + v0 .
(ii) By solving an appropriate differential equation and using the result from part (b) (i), find an expression for smax in terms of v0 . [7]
Let v (T – k) represent the particle’s velocity k seconds before it reaches smax , where v (T – k) = (1 + v0) e-(T – k) – 1 .
(c) By using the result to part (b) (i), show that v (T – k) = ek – 1 . [2]
Similarly, let v (T + k) represent the particle’s velocity k seconds after it reaches smax .
(d) Deduce a similar expression for v (T + k) in terms of k . [2]
(e) Hence, show that v (T – k) + v (T + k) ≥ 0 . [3]
▶️Answer/Explanation
Ans:
(a) Since $a=\frac{\text{d}v}{\text{d}t}$, and $a=-\left(1+v\right)$, we have
$$\begin{eqnarray}
\frac{\text{d}v}{\text{d}t} = -1-v \nonumber \\
\frac{\text{d}v}{\text{d}t}+v = -1.
\end{eqnarray}$$
Let $\text{I}\left(x\right)=\text{e}^{\int 1 \text{d}t}=\text{e}^t$.<br>
Then, we have
$$\begin{eqnarray}
\frac{\text{d}}{\text{d}t}\left(v\text{e}^t\right) = -\text{e}^t \nonumber \\
v\text{e}^t = -\int\text{e}^t \text{d}t \nonumber \\
v\text{e}^t = -\text{e}^t+c \nonumber \\
v = c\text{e}^{-t}-1.
\end{eqnarray}$$
Since $v=v_0$ when $t=0$, we have $c=1+v_0$, i.e., $v=\left(1+v_0\right)\text{e}^{-t}-1$.<br>
(b)(i) At $s_{\text{max}}$, $t=T$, i.e., we have
$$\begin{eqnarray}
v\left(T\right) = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T}-1 = 0 \nonumber \\
\left(1+v_0\right)\text{e}^{-T} = 1 \nonumber \\
1+v_0 = \text{e}^T.
\end{eqnarray}$$
(b)(ii) Since $\frac{\text{d}s}{\text{d}t}=\left(1+v_0\right)\text{e}^{-t}-1$, integrating both sides with respect to $t$, we have
$$\begin{eqnarray}
s &=& \int\left(1+v_0\right)\text{e}^{-t}-1\text{d}t \nonumber \\
&=& -\left(1+v_0\right)\text{e}^{-t}-t+c.
\end{eqnarray}$$
When $t=0$, $s=0$, i.e.,
$$\begin{eqnarray}
0 = -\left(1+v_0\right)+c \nonumber \\
c = \left(1+v_0\right).
\end{eqnarray}$$
Thus, $s=\left(1+v_0\right)-\left(1+v_0\right)\text{e}^{-t}-t$.<br>
Since from (b)(i) we have $1+v_0=\text{e}^T$, $T=\ln\left(1+v_0\right)$, i.e., $s_{\text{max}}=v_0-\ln \left(1+v_0\right)$.<br>
(c) Since $\text{e}^T=1+v_0$, we have $\left(1+v_0\right)\text{e}^{-T}=1$, i.e.,
$$\begin{eqnarray}
v\left(T-k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T-k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^k-1 \nonumber \\
&=& \text{e}^k-1.
\end{eqnarray}$$
(d) Similarly, as in (c),
$$\begin{eqnarray}
v\left(T+k\right) &=& \left(1+v_0\right)\text{e}^{-\left(T+k\right)}-1 \nonumber \\
&=& \left(1+v_0\right)\text{e}^{-T}\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^{-k}-1.
\end{eqnarray}$$
(e)
$$\begin{eqnarray}
v\left(T-k\right)+v\left(T+k\right) &=& \text{e}^k-1+\text{e}^{-k}-1 \nonumber \\
&=& \text{e}^k+\text{e}^{-k}-2 \nonumber \\
&=& \frac{\text{e}^{2k}-2\text{e}^k+1}{\text{e}^k} \nonumber \\
&=& \frac{\left(\text{e}^k-1\right)^2}{\text{e}^k} \geq 0.
\end{eqnarray}$$
Question
Consider the function f defined by f (x) = ln (x2 – 16) for x > 4 .
The following diagram shows part of the graph of f which crosses the x-axis at point A, with
coordinates ( a , 0 ). The line L is the tangent to the graph of f at the point B.
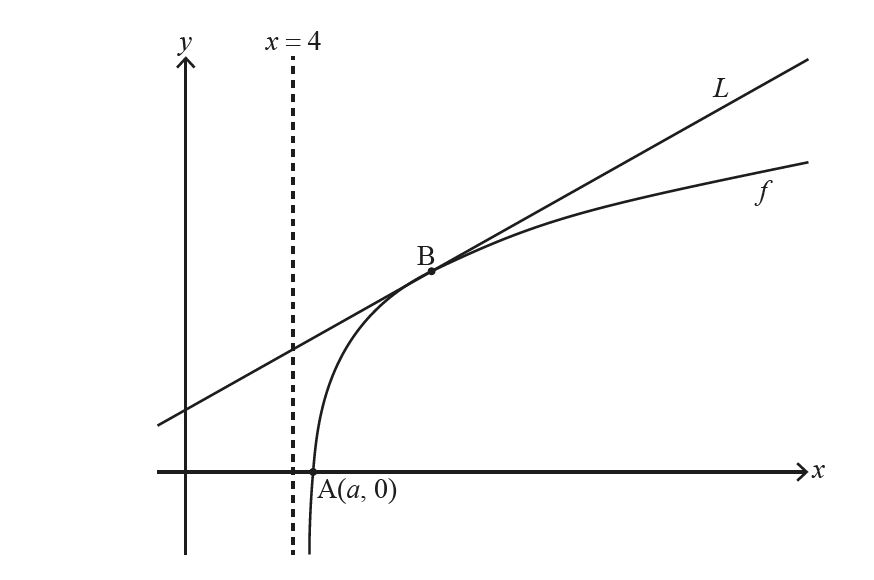
(a) Find the exact value of a . [3]
(b) Given that the gradient of L is \(\frac{1}{3}\) , find the x-coordinate of B. [6]
▶️Answer/Explanation
Ans:
(a) When f(x)=0, we have
ln(x2−16)=0
x2−16=1
x=±√17
However, since x>4, we have x=√17
(b) Differentiating f(x) with respect to x, we have f′(x)= \(\frac{2x}{x^2-16}\)
At B, f′(x)=\(\frac{1}{3}\) , i.e., we have
x2−16=6x
x2−6x−16=0
(x+2)(x−8)=0.
Thus, x=−2 (reject) or x=8.
Question
a.Using the definition of a derivative as \(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h) – f(x)}}{h}} \right)\) , show that the derivative of \(\frac{1}{{2x + 1}}{\text{ is }}\frac{{ – 2}}{{{{(2x + 1)}^2}}}\).[4]
b.Prove by induction that the \({n^{{\text{th}}}}\) derivative of \({(2x + 1)^{ – 1}}\) is \({( – 1)^n}\frac{{{2^n}n!}}{{{{(2x + 1)}^{n + 1}}}}\).[9]
▶️Answer/Explanation
Markscheme
let \(f(x) = \frac{1}{{2x + 1}}\) and using the result \(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h) – f(x)}}{h}} \right)\)
\(f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{\frac{1}{{2(x + h) + 1}} – \frac{1}{{2x + 1}}}}{h}} \right)\) M1A1
\( \Rightarrow f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{[2x + 1] – [2(x + h) + 1]}}{{h[2(x + h) + 1][2x + 1]}}} \right)\) A1
\( \Rightarrow f'(x) = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{ – 2}}{{[2(x + h) + 1][2x + 1]}}} \right)\) A1
\( \Rightarrow f'(x) = \frac{{ – 2}}{{{{(2x + 1)}^2}}}\) AG
[4 marks]
let \(y = \frac{1}{{2x + 1}}\)
we want to prove that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = {( – 1)^n}\frac{{{2^n}n!}}{{{{(2x + 1)}^{n + 1}}}}\)
let \(n = 1 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = {( – 1)^1}\frac{{{2^1}1!}}{{{{(2x + 1)}^{1 + 1}}}}\) M1
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 2}}{{{{(2x + 1)}^2}}}\) which is the same result as part (a)
hence the result is true for \(n = 1\) R1
assume the result is true for \(n = k{\text{ : }}\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = {( – 1)^k}\frac{{{2^k}k!}}{{{{(2x + 1)}^{k + 1}}}}\) M1
\(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left[ {{{( – 1)}^k}\frac{{{2^k}k!}}{{{{(2x + 1)}^{k + 1}}}}} \right]\) M1
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left[ {{{( – 1)}^k}{2^k}k!{{(2x + 1)}^{ – k – 1}}} \right]\) (A1)
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^k}{2^k}k!( – k – 1){(2x + 1)^{ – k – 2}} \times 2\) A1
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^{k + 1}}{2^{k + 1}}(k + 1)!{(2x + 1)^{ – k – 2}}\) (A1)
\( \Rightarrow \frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = {( – 1)^{k + 1}}\frac{{{2^{k + 1}}(k + 1)!}}{{{{(2x + 1)}^{k + 2}}}}\) A1
hence if the result is true for \(n = k\) , it is true for \(n = k + 1\)
since the result is true for \(n = 1\) , the result is proved by mathematical induction R1
Note: Only award final R1 if all the M marks have been gained.
[9 marks]
Question
A curve is defined by \(xy = {y^2} + 4\).
a.Show that there is no point where the tangent to the curve is horizontal.[4]
b.Find the coordinates of the points where the tangent to the curve is vertical.[4]
▶️Answer/Explanation
Markscheme
\(x\frac{{{\text{d}}y}}{{{\text{d}}x}} + y = 2y\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
a horizontal tangent occurs if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) so \(y = 0\) M1
we can see from the equation of the curve that this solution is not possible \((0 = 4)\) and so there is not a horizontal tangent R1
[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{{2y – x}}\) or equivalent with \(\frac{{{\text{d}}x}}{{{\text{d}}y}}\)
the tangent is vertical when \(2y = x\) M1
substitute into the equation to give \(2{y^2} = {y^2} + 4\) M1
\(y = \pm 2\) A1
coordinates are \((4,{\text{ }}2),{\text{ }}( – 4,{\text{ }} – 2)\) A1
[4 marks]
Total [8 marks]
Question
A curve is defined by \(xy = {y^2} + 4\).
a.Show that there is no point where the tangent to the curve is horizontal.[4]
b.Find the coordinates of the points where the tangent to the curve is vertical.[4]
▶️Answer/Explanation
Markscheme
\(x\frac{{{\text{d}}y}}{{{\text{d}}x}} + y = 2y\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
a horizontal tangent occurs if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) so \(y = 0\) M1
we can see from the equation of the curve that this solution is not possible \((0 = 4)\) and so there is not a horizontal tangent R1
[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{y}{{2y – x}}\) or equivalent with \(\frac{{{\text{d}}x}}{{{\text{d}}y}}\)
the tangent is vertical when \(2y = x\) M1
substitute into the equation to give \(2{y^2} = {y^2} + 4\) M1
\(y = \pm 2\) A1
coordinates are \((4,{\text{ }}2),{\text{ }}( – 4,{\text{ }} – 2)\) A1
[4 marks]
Total [8 marks]
Question
Find the \(x\)-coordinates of all the points on the curve \(y = 2{x^4} + 6{x^3} + \frac{7}{2}{x^2} – 5x + \frac{3}{2}\) at which
the tangent to the curve is parallel to the tangent at \(( – 1,{\text{ }}6)\).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 8{x^3} + 18{x^2} + 7x – 5\) A1
when \(x = – 1,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2\) A1
\(8{x^3} + 18{x^2} + 7x – 5 = – 2\) M1
\(8{x^3} + 18{x^2} + 7x – 3 = 0\)
\((x + 1)\) is a factor A1
\(8{x^3} + 18{x^2} + 7x – 3 = (x + 1)(8{x^2} + 10x – 3)\) (M1)
Note: M1 is for attempting to find the quadratic factor.
\((x + 1)(4x – 1)(2x + 3) = 0\)
\((x = – 1),{\text{ }}x = 0.25,{\text{ }}x = – 1.5\) (M1)A1
Note: M1 is for an attempt to solve their quadratic factor.
[7 marks]
Question
The function \(f\) is defined as \(f(x) = a{x^2} + bx + c\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{R}\).
Hayley conjectures that \(\frac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}} = \frac{{f'({x_2}) + f'({x_1})}}{2},{\text{ }}x1 \ne x2\).
Show that Hayley’s conjecture is correct.
▶️Answer/Explanation
Markscheme
\(\frac{{f({x_2}) – f({x_1})}}{{{x_2} – {x_1}}} = \frac{{ax_2^2 + b{x_2} + c – (ax_1^2 + b{x_1} + c)}}{{{x_2} – {x_1}}}\) (M1)
\( = \frac{{a(x_2^2 – x_1^2) + b({x_2} – {x_1})}}{{{x_2} – {x_1}}}\) A1
\( = \frac{{a({x_2} – {x_1})({x_2} + {x_1}) + b({x_2} – {x_1})}}{{{x_2} – {x_1}}}\) (A1)
\( = a({x_2} + {x_1}) + b\,\,\,\,\,({x_1} \ne {x_2})\) A1
\(\frac{{f'({x_2}) + f'({x_1})}}{2} = \frac{{(2a{x_2} + b) + (2a{x_1} + b)}}{2}\) M1
\( = \frac{{2a({x_2} + {x_1}) + 2b}}{2}\)
\( = a({x_2} + {x_1}) + b\) A1
so Hayley’s conjecture is correct AG
[6 marks]
Question
A curve has equation \(3x – 2{y^2}{{\text{e}}^{x – 1}} = 2\).
a.Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of \(x\) and \(y\).[5]
b.Find the equations of the tangents to this curve at the points where the curve intersects the line \(x = 1\).[4]
▶️Answer/Explanation
Markscheme
attempt to differentiate implicitly M1
\(3 – \left( {4y\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2{y^2}} \right){{\text{e}}^{x – 1}} = 0\) A1A1A1
Note: Award A1 for correctly differentiating each term.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 \bullet {{\text{e}}^{1 – x}} – 2{y^2}}}{{4y}}\) A1
Note: This final answer may be expressed in a number of different ways.
[5 marks]
\(3 – 2{y^2} = 2 \Rightarrow {y^2} = \frac{1}{2} \Rightarrow y = \pm \sqrt {\frac{1}{2}} \) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{3 – 2 \bullet \frac{1}{2}}}{{ \pm 4\sqrt {\frac{1}{2}} }} = \pm \frac{{\sqrt 2 }}{2}\) M1
at \(\left( {1,{\text{ }}\sqrt {\frac{1}{2}} } \right)\) the tangent is \(y – \sqrt {\frac{1}{2}} = \frac{{\sqrt 2 }}{2}(x – 1)\) and A1
at \(\left( {1,{\text{ }} – \sqrt {\frac{1}{2}} } \right)\) the tangent is \(y + \sqrt {\frac{1}{2}} = – \frac{{\sqrt 2 }}{2}(x – 1)\) A1
Note: These equations simplify to \(y = \pm \frac{{\sqrt 2 }}{2}x\).
Note: Award A0M1A1A0 if just the positive value of \(y\) is considered and just one tangent is found.
[4 marks]
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
a.Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
b.Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).[2]
c.Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).[2]
d.Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).[2]
e.Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.[3]
f.Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).[6]
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
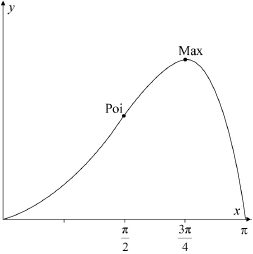
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
a.i.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);[2]
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);[4]
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).[2]
Find \(\int {f(x)\cos x{\text{d}}x} \).[5]
By finding \(g'(x)\) explain why \(g\) is an increasing function.[4]
▶️Answer/Explanation
Markscheme
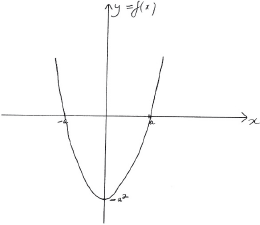
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
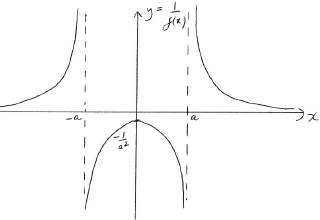
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
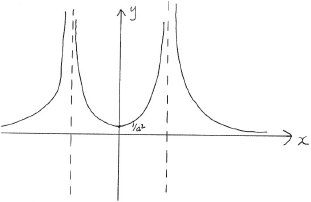
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Question
Consider the function \({f_n}(x) = (\cos 2x)(\cos 4x) \ldots (\cos {2^n}x),{\text{ }}n \in {\mathbb{Z}^ + }\).
a.Determine whether \({f_n}\) is an odd or even function, justifying your answer.[2]
b.By using mathematical induction, prove that
\({f_n}(x) = \frac{{\sin {2^{n + 1}}x}}{{{2^n}\sin 2x}},{\text{ }}x \ne \frac{{m\pi }}{2}\) where \(m \in \mathbb{Z}\).[8]
c.Hence or otherwise, find an expression for the derivative of \({f_n}(x)\) with respect to \(x\).[3]
d.Show that, for \(n > 1\), the equation of the tangent to the curve \(y = {f_n}(x)\) at \(x = \frac{\pi }{4}\) is \(4x – 2y – \pi = 0\).[8]
▶️Answer/Explanation
Markscheme
even function A1
since \(\cos kx = \cos ( – kx)\) and \({f_n}(x)\) is a product of even functions R1
OR
even function A1
since \((\cos 2x)(\cos 4x) \ldots = \left( {\cos ( – 2x)} \right)\left( {\cos ( – 4x)} \right) \ldots \) R1
Note: Do not award A0R1.
[2 marks]
consider the case \(n = 1\)
\(\frac{{\sin 4x}}{{2\sin 2x}} = \frac{{2\sin 2x\cos 2x}}{{2\sin 2x}} = \cos 2x\) M1
hence true for \(n = 1\) R1
assume true for \(n = k\), ie, \((\cos 2x)(\cos 4x) \ldots (\cos {2^k}x) = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\) M1
Note: Do not award M1 for “let \(n = k\)” or “assume \(n = k\)” or equivalent.
consider \(n = k + 1\):
\({f_{k + 1}}(x) = {f_k}(x)(\cos {2^{k + 1}}x)\) (M1)
\( = \frac{{\sin {2^{k + 1}}x}}{{{2^k}\sin 2x}}\cos {2^{k + 1}}x\) A1
\( = \frac{{2\sin {2^{k + 1}}x\cos {2^{k + 1}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
\( = \frac{{\sin {2^{k + 2}}x}}{{{2^{k + 1}}\sin 2x}}\) A1
so \(n = 1\) true and \(n = k\) true \( \Rightarrow n = k + 1\) true. Hence true for all \(n \in {\mathbb{Z}^ + }\) R1
Note: To obtain the final R1, all the previous M marks must have been awarded.
[8 marks]
attempt to use \(f’ = \frac{{vu’ – uv’}}{{{v^2}}}\) (or correct product rule) M1
\({f’_n}(x) = \frac{{({2^n}\sin 2x)({2^{n + 1}}\cos {2^{n + 1}}x) – (\sin {2^{n + 1}}x)({2^{n + 1}}\cos 2x)}}{{{{({2^n}\sin 2x)}^2}}}\) A1A1
Note: Award A1 for correct numerator and A1 for correct denominator.
[3 marks]
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{\left( {{2^n}\sin \frac{\pi }{2}} \right)\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right) – \left( {\sin {2^{n + 1}}\frac{\pi }{4}} \right)\left( {{2^{n + 1}}\cos \frac{\pi }{2}} \right)}}{{{{\left( {{2^n}\sin \frac{\pi }{2}} \right)}^2}}}\) (M1)(A1)
\({f’_n}\left( {\frac{\pi }{4}} \right) = \frac{{({2^n})\left( {{2^{n + 1}}\cos {2^{n + 1}}\frac{\pi }{4}} \right)}}{{{{({2^n})}^2}}}\) (A1)
\( = 2\cos {2^{n + 1}}\frac{\pi }{4}{\text{ }}( = 2\cos {2^{n – 1}}\pi )\) A1
\({f’_n}\left( {\frac{\pi }{4}} \right) = 2\) A1
\({f_n}\left( {\frac{\pi }{4}} \right) = 0\) A1
Note: This A mark is independent from the previous marks.
\(y = 2\left( {x – \frac{\pi }{4}} \right)\) M1A1
\(4x – 2y – \pi = 0\) AG
[8 marks]