Question
Given that the graph of \(y = {x^3} – 6{x^2} + kx – 4\) has exactly one point at which the gradient is zero, find the value of k .
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} – 12x + k\) M1A1
For use of discriminant \({b^2} – 4ac = 0\) or completing the square \(3{(x – 2)^2} + k – 12\) (M1)
\(144 – 12k = 0\) (A1)
Note: Accept trial and error, sketches of parabolas with vertex (2,0) or use of second derivative.
\(k = 12\) A1
[5 marks]
Examiners report
Generally candidates answer this question well using a diversity of methods. Surprisingly, a small number of candidates were successful in answering this question using the discriminant of the quadratic and in many cases reverted to trial and error to obtain the correct answer.
Question
a.Sketch the curve \(y = \frac{{\cos x}}{{\sqrt {{x^2} + 1} }},{\text{ }} – 4 \leqslant x \leqslant 4\) showing clearly the coordinates of the x-intercepts, any maximum points and any minimum points.[4]
b.Write down the gradient of the curve at x = 1 .[1]
c.Find the equation of the normal to the curve at x = 1 .[3]
▶️Answer/Explanation
Markscheme
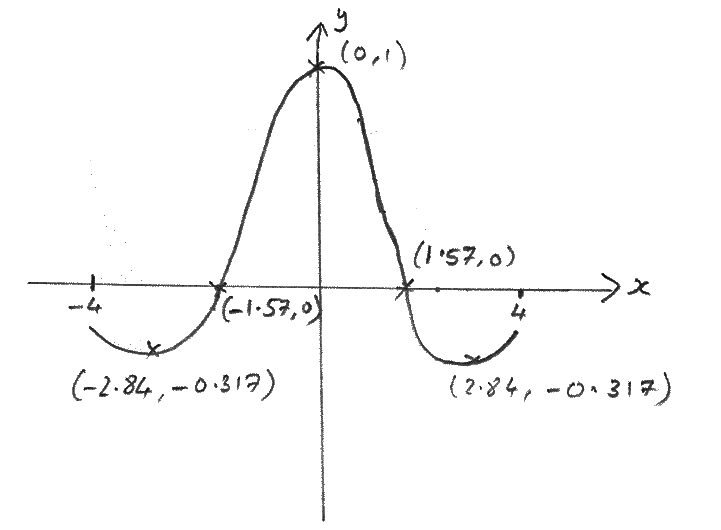A1A1A1A1
Note: Award A1 for correct shape. Do not penalise if too large a domain is used,
A1 for correct x-intercepts,
A1 for correct coordinates of two minimum points,
A1 for correct coordinates of maximum point.
Accept answers which correctly indicate the position of the intercepts, maximum point and minimum points.
[4 marks]
gradient at x = 1 is –0.786 A1
[1 mark]
gradient of normal is \(\frac{{ – 1}}{{ – 0.786}}( = 1.272…)\) (A1)
when x = 1, y = 0.3820… (A1)
Equation of normal is y – 0.382 = 1.27(x – 1) A1
\(( \Rightarrow y = 1.27x – 0.890)\)
[3 marks]
Question
Consider the curve, \(C\) defined by the equation \({y^2} – 2xy = 5 – {{\text{e}}^x}\). The point A lies on \(C\) and has coordinates \((0,{\text{ }}a),{\text{ }}a > 0\).
a.Find the value of \(a\).[2]
b.Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\).[4]
c.Find the equation of the normal to \(C\) at the point A.[3]
d.Find the coordinates of the second point at which the normal found in part (c) intersects \(C\).[4]
e.Given that \(v = {y^3},{\text{ }}y > 0\), find \(\frac{{{\text{d}}v}}{{{\text{d}}x}}\) at \(x = 0\).[3]
▶️Answer/Explanation
\({a^2} = 5 – 1\) (M1)
\(a = 2\) A1
[2 marks]
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} – \left( {2x\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2y} \right) = – {{\text{e}}^x}\) M1A1A1A1
Note: Award M1 for an attempt at implicit differentiation, A1 for each part.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\) AG
[4 marks]
at \(x = 0,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{3}{4}\) (A1)
finding the negative reciprocal of a number (M1)
gradient of normal is \( – \frac{4}{3}\)
\(y = – \frac{4}{3}x + 2\) A1
[3 marks]
substituting linear expression (M1)
\({\left( { – \frac{4}{3}x + 2} \right)^2} – 2x\left( { – \frac{4}{3}x + 2} \right) + {{\text{e}}^x} – 5 = 0\) or equivalent
\(x = 1.56\) (M1)A1
\(y = – 0.0779\) A1
\((1.56,{\text{ }} – 0.0779)\)
[4 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3 \times 4 \times \frac{3}{4} = 9\) A1
[3 marks]
Question
The curve \(C\) is defined by equation \(xy – \ln y = 1,{\text{ }}y > 0\).
a.Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of \(x\) and \(y\).[4]
b.Determine the equation of the tangent to \(C\) at the point \(\left( {\frac{2}{{\text{e}}},{\text{ e}}} \right)\)[3]
▶️Answer/Explanation
Markscheme
\(y + x\frac{{{\text{d}}y}}{{{\text{d}}x}} – \frac{1}{y}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1A1
Note: Award A1 for the first two terms, A1 for the third term and the 0.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{{y^2}}}{{1 – xy}}\) A1
Note: Accept \(\frac{{ – {y^2}}}{{\ln y}}\).
Note: Accept \(\frac{{ – y}}{{x – \frac{1}{y}}}\).
[4 marks]
\({m_T} = \frac{{{{\text{e}}^2}}}{{1 – {\text{e}} \times \frac{2}{{\text{e}}}}}\) (M1)
\({m_T} = – {{\text{e}}^2}\) (A1)
\(y – {\text{e}} = – {{\text{e}}^2}x + 2{\text{e}}\)
\( – {{\text{e}}^2}x – y + 3{\text{e}} = 0\) or equivalent A1
Note: Accept \(y = – 7.39x + 8.15\).
[3 marks]
Question
Consider the curve defined by the equation \(4{x^2} + {y^2} = 7\).
a.Find the equation of the normal to the curve at the point \(\left( {1,{\text{ }}\sqrt 3 } \right)\).[6]
b.Find the volume of the solid formed when the region bounded by the curve, the \(x\)-axis for \(x \geqslant 0\) and the \(y\)-axis for \(y \geqslant 0\) is rotated through \(2\pi \) about the \(x\)-axis.[3]
▶️Answer/Explanation
Markscheme
METHOD 1
\(4{x^2} + {y^2} = 7\)
\(8x + 2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (M1)(A1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{y}\)
Note: Award M1A1 for finding \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2.309 \ldots \) using any alternative method.
hence gradient of normal \( = \frac{y}{{4x}}\) (M1)
hence gradient of normal at \(\left( {1,{\text{ }}\sqrt 3 } \right)\) is \(\frac{{\sqrt 3 }}{4}\,\,\,( = 0.433)\) (A1)
hence equation of normal is \(y – \sqrt 3 = \frac{{\sqrt 3 }}{4}(x – 1)\) (M1)A1
\(\left( {y = \frac{{\sqrt 3 }}{4}x + \frac{{3\sqrt 3 }}{4}} \right)\,\,\,(y = 0.433x + 1.30)\)
METHOD 2
\(4{x^2} + {y^2} = 7\)
\(y = \sqrt {7 – 4{x^2}} \) (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{4x}}{{\sqrt {7 – 4{x^2}} }}\) (A1)
Note: Award M1A1 for finding \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 2.309 \ldots \) using any alternative method.
hence gradient of normal \( = \frac{{\sqrt {7 – 4{x^2}} }}{{4x}}\) (M1)
hence gradient of normal at \(\left( {1,{\text{ }}\sqrt 3 } \right)\) is \(\frac{{\sqrt 3 }}{4}\,\,\,( = 0.433)\) (A1)
hence equation of normal is \(y – \sqrt 3 = \frac{{\sqrt 3 }}{4}(x – 1)\) (M1)A1
\(\left( {y = \frac{{\sqrt 3 }}{4}x + \frac{{3\sqrt 3 }}{4}} \right)\,\,\,(y = 0.433x + 1.30)\)
[6 marks]
Use of \(V = \pi \int\limits_0^{\frac{{\sqrt 7 }}{2}} {{y^2}{\text{d}}x} \)
\(V = \pi \int\limits_0^{\frac{{\sqrt 7 }}{2}} {\left( {7 – 4{x^2}} \right){\text{d}}x} \) (M1)(A1)
Note: Condone absence of limits or incorrect limits for M mark.
Do not condone absence of or multiples of \(\pi \).
\( = 19.4\,\,\,\left( { = \frac{{7\sqrt 7 \pi }}{3}} \right)\) A1
[3 marks]
Examiners report
[N/A]
[N/A]
Question
Consider the function \(f(x) = \frac{{\sqrt x }}{{\sin x}},{\text{ }}0 < x < \pi \).
Consider the region bounded by the curve \(y = f(x)\), the \(x\)-axis and the lines \(x = \frac{\pi }{6},{\text{ }}x = \frac{\pi }{3}\).
a.i.Show that the \(x\)-coordinate of the minimum point on the curve \(y = f(x)\) satisfies the equation \(\tan x = 2x\).[5]
a.ii.Determine the values of \(x\) for which \(f(x)\) is a decreasing function.[2]
b.Sketch the graph of \(y = f(x)\) showing clearly the minimum point and any asymptotic behaviour.[3]
c.Find the coordinates of the point on the graph of \(f\) where the normal to the graph is parallel to the line \(y = – x\).[4]
d.This region is now rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume of revolution.[3]
▶️Answer/Explanation
Markscheme
attempt to use quotient rule or product rule M1
\(f’(x) = \frac{{\sin x\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \sqrt x \cos x}}{{{{\sin }^2}x}}{\text{ }}\left( { = \frac{1}{{2\sqrt x \sin x}} – \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}} \right)\) A1A1
Note: Award A1 for \(\frac{1}{{2\sqrt x \sin x}}\) or equivalent and A1 for \( – \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}\) or equivalent.
setting \(f’(x) = 0\) M1
\(\frac{{\sin x}}{{2\sqrt x }} – \sqrt x \cos x = 0\)
\(\frac{{\sin x}}{{2\sqrt x }} = \sqrt x \cos x\) or equivalent A1
\(\tan x = 2x\) AG
[5 marks]
\(x = 1.17\)
\(0 < x \leqslant 1.17\) A1A1
Note: Award A1 for \(0 < x\) and A1 for \(x \leqslant 1.17\). Accept \(x < 1.17\).
[2 marks]
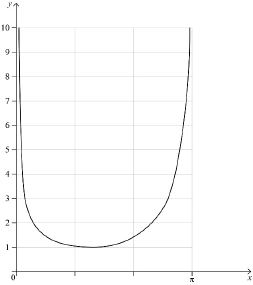
concave up curve over correct domain with one minimum point above the \(x\)-axis. A1
approaches \(x = 0\) asymptotically A1
approaches \(x = \pi \) asymptotically A1
Note: For the final A1 an asymptote must be seen, and \(\pi \) must be seen on the \(x\)-axis or in an equation.
[3 marks]
\(f’(x){\text{ }}\left( { = \frac{{\sin x\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \sqrt x \cos x}}{{{{\sin }^2}x}}} \right) = 1\) (A1)
attempt to solve for \(x\) (M1)
\(x = 1.96\) A1
\(y = f(1.96 \ldots )\)
\( = 1.51\) A1
[4 marks]
\(V = \pi \int_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{x{\text{d}}x}}{{{{\sin }^2}x}}} \) (M1)(A1)
Note: M1 is for an integral of the correct squared function (with or without limits and/or \(\pi \)).
\( = 2.68{\text{ }}( = 0.852\pi )\) A1
Question
The following graph shows the two parts of the curve defined by the equation \({x^2}y = 5 – {y^4}\), and the normal to the curve at the point P(2 , 1).
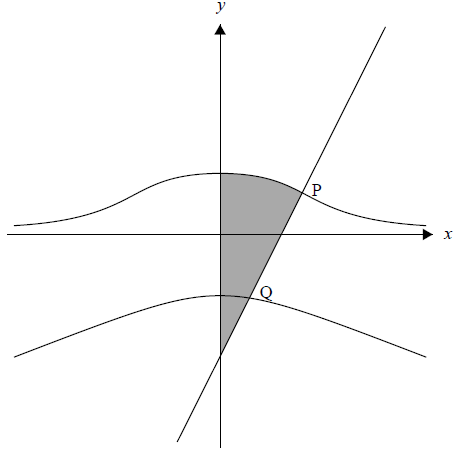
a.Show that there are exactly two points on the curve where the gradient is zero.[7]
b.Find the equation of the normal to the curve at the point P.[5]
c.The normal at P cuts the curve again at the point Q. Find the \(x\)-coordinate of Q.[3]
d.The shaded region is rotated by 2\(\pi \) about the \(y\)-axis. Find the volume of the solid formed.[7]
▶️Answer/Explanation
Markscheme
differentiating implicitly: M1
\(2xy + {x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4{y^3}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) A1A1
Note: Award A1 for each side.
if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) then either \(x = 0\) or \(y = 0\) M1A1
\(x = 0 \Rightarrow \) two solutions for \(y\left( {y = \pm \sqrt[4]{5}} \right)\) R1
\(y = 0\) not possible (as 0 ≠ 5) R1
hence exactly two points AG
Note: For a solution that only refers to the graph giving two solutions at \(x = 0\) and no solutions for \(y = 0\) award R1 only.
[7 marks]
at (2, 1) \(4 + 4\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{2}\) (A1)
gradient of normal is 2 M1
1 = 4 + c (M1)
equation of normal is \(y = 2x – 3\) A1
[5 marks]
substituting (M1)
\({x^2}\left( {2x – 3} \right) = 5 – {\left( {2x – 3} \right)^4}\) or \({\left( {\frac{{y + 3}}{2}} \right)^2}\,y = 5 – {y^4}\) (A1)
\(x = 0.724\) A1
[3 marks]
recognition of two volumes (M1)
volume \(1 = \pi \int_1^{\sqrt[4]{5}} {\frac{{5 – {y^4}}}{y}} {\text{d}}y\left( { = 101\pi = 3.178 \ldots } \right)\) M1A1A1
Note: Award M1 for attempt to use \(\pi \int {{x^2}} {\text{d}}y\), A1 for limits, A1 for \({\frac{{5 – {y^4}}}{y}}\) Condone omission of \(\pi \) at this stage.
volume 2
EITHER
\( = \frac{1}{3}\pi \times {2^2} \times 4\left( { = 16.75 \ldots } \right)\) (M1)(A1)
OR
\( = \pi \int_{ – 3}^1 {{{\left( {\frac{{y + 3}}{2}} \right)}^2}} {\text{d}}y\left( { = \frac{{16\pi }}{3} = 16.75 \ldots } \right)\) (M1)(A1)
THEN
total volume = 19.9 A1
[7 marks]