Question
The diagram shows the plan of an art gallery a metres wide. [AB] represents a doorway, leading to an exit corridor b metres wide. In order to remove a painting from the art gallery, CD (denoted by L ) is measured for various values of \(\alpha \) , as represented in the diagram.
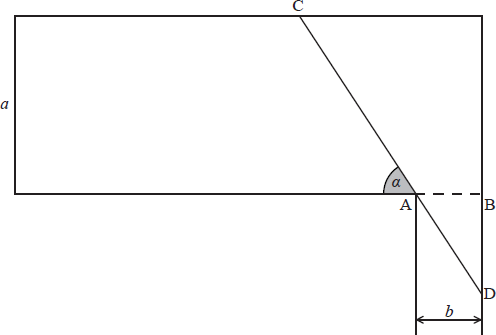
If \(\alpha \) is the angle between [CD] and the wall, show that \(L = \frac{a }{{\sin \alpha }} + \frac{b}{{\cos \alpha }}{\text{, }}0 < \alpha < \frac{\pi }{2}\).
If a = 5 and b = 1, find the maximum length of a painting that can be removed through this doorway.
Let a = 3k and b = k .
Find \(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }}\).
Let a = 3k and b = k .
Find, in terms of k , the maximum length of a painting that can be removed from the gallery through this doorway.
Let a = 3k and b = k .
Find the minimum value of k if a painting 8 metres long is to be removed through this doorway.
Answer/Explanation
Markscheme
\(L = {\text{CA}} + {\text{AD}}\) M1
\({\text{sin}}\alpha {\text{ = }}\frac{a}{{{\text{CA}}}} \Rightarrow {\text{CA}} = \frac{a}{{\sin \alpha }}\) A1
\(\cos \alpha = \frac{b}{{{\text{AD}}}} \Rightarrow {\text{AD}} = \frac{b}{{\cos \alpha }}\) A1
\(L = \frac{a}{{\sin \alpha }} + \frac{b}{{\cos \alpha }}\) AG
[2 marks]
\(a = 5{\text{ and }}b = 1 \Rightarrow L = \frac{5}{{\sin \alpha }} + \frac{1}{{\cos \alpha }}\)
METHOD 1
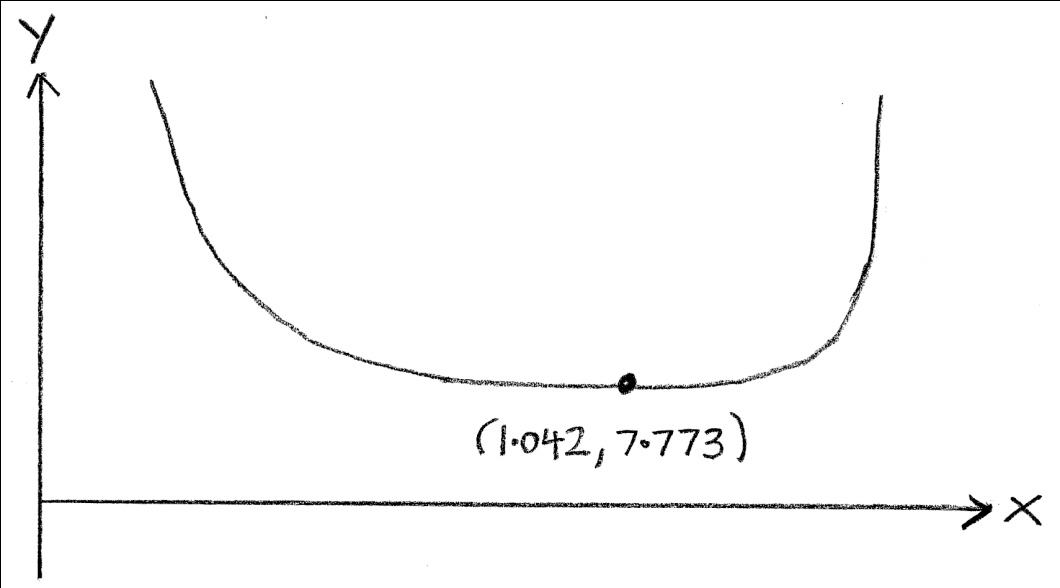 (M1)
(M1)
minimum from graph \( \Rightarrow L = 7.77\) (M1)A1
minimum of L gives the max length of the painting R1
[4 marks]
METHOD 2
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 5\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{\sin \alpha }}{{{{\cos }^2}\alpha }}\) (M1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = 5 \Rightarrow \tan \alpha = \sqrt[{3{\text{ }}}]{5}{\text{ }}(\alpha = 1.0416…)\) (M1)
minimum of L gives the max length of the painting R1
maximum length = 7.77 A1
[4 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{k\sin \alpha }}{{{{\cos }^2}\alpha }}\,\,\,\,\,{\text{(or equivalent)}}\) M1A1A1
[3 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k{{\cos }^3}\alpha + k{{\sin }^3}\alpha }}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }}\) (A1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = \frac{{3k}}{k} \Rightarrow \tan \alpha = \sqrt[3]{3}\,\,\,\,\,(\alpha = 0.96454…)\) M1A1
\(\tan \alpha = \sqrt[3]{3} \Rightarrow \frac{1}{{\cos \alpha }} = \sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(1.755…)\) (A1)
\({\text{and }}\frac{1}{{\sin \alpha }} = \frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}\,\,\,\,\,(1.216…)\) (A1)
\(L = 3k\left( {\frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}} \right) + k\sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(L = 5.405598…k)\) A1 N4
[6 marks]
\(L \leqslant 8 \Rightarrow k \geqslant 1.48\) M1A1
the minimum value is 1.48
[2 marks]
Examiners report
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Question
The function f has inverse \({f^{ – 1}}\) and derivative \(f'(x)\) for all \(x \in \mathbb{R}\). For all functions with these properties you are given the result that for \(a \in \mathbb{R}\) with \(b = f(a)\) and \(f'(a) \ne 0\)
\[({f^{ – 1}})'(b) = \frac{1}{{f'(a)}}.\]
Verify that this is true for \(f(x) = {x^3} + 1\) at x = 2.
Given that \(g(x) = x{{\text{e}}^{{x^2}}}\), show that \(g'(x) > 0\) for all values of x.
Using the result given at the start of the question, find the value of the gradient function of \(y = {g^{ – 1}}(x)\) at x = 2.
(i) With f and g as defined in parts (a) and (b), solve \(g \circ f(x) = 2\).
(ii) Let \(h(x) = {(g \circ f)^{ – 1}}(x)\). Find \(h'(2)\).
Answer/Explanation
Markscheme
\(f(2) = 9\) (A1)
\({f^{ – 1}}(x) = {(x – 1)^{\frac{1}{3}}}\) A1
\(({f^{ – 1}})'(x) = \frac{1}{3}{(x – 1)^{ – \frac{2}{3}}}\) (M1)
\(({f^{ – 1}})'(9) = \frac{1}{{12}}\) A1
\(f'(x) = 3{x^2}\) (M1)
\(\frac{1}{{f'(2)}} = \frac{1}{{3 \times 4}} = \frac{1}{{12}}\) A1
Note: The last M1 and A1 are independent of previous marks.
[6 marks]
\(g'(x) = {{\text{e}}^{{x^2}}} + 2{x^2}{{\text{e}}^{{x^2}}}\) M1A1
\(g'(x) > 0\) as each part is positive R1
[3 marks]
to find the x-coordinate on \(y = g(x)\) solve
\(2 = x{{\text{e}}^{{x^2}}}\) (M1)
\(x = 0.89605022078 \ldots \) (A1)
gradient \( = ({g^{ – 1}})'(2) = \frac{1}{{g'(0.896 \ldots )}}\) (M1)
\( = \frac{1}{{{{\text{e}}^{{{(0.896 \ldots )}^2}}}\left( {1 + 2 \times {{(0.896 \ldots )}^2}} \right)}} = 0.172\) to 3sf A1
(using the \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) function on gdc \(g'(0.896 \ldots ) = 5.7716028 \ldots \)
\(\frac{1}{{g'(0.896 \ldots )}} = 0.173\)
[4 marks]
(i) \(({x^3} + 1){{\text{e}}^{{{({x^3} + 1)}^2}}} = 2\) A1
\(x = – 0.470191 \ldots \) A1
(ii) METHOD 1
\((g \circ f)'(x) = 3{x^2}{{\text{e}}^{{{({x^3} + 1)}^2}}}\left( {2{{({x^3} + 1)}^2} + 1} \right)\) (M1)(A1)
\((g \circ f)'( – 0.470191 \ldots ) = 3.85755 \ldots \) (A1)
\(h'(2) = \frac{1}{{3.85755 \ldots }} = 0.259{\text{ }}(232 \ldots )\) A1
Note: The solution can be found without the student obtaining the explicit form of the composite function.
METHOD 2
\(h(x) = ({f^{ – 1}} \circ {g^{ – 1}})(x)\) A1
\(h'(x) = ({f^{ – 1}})’\left( {{g^{ – 1}}(x)} \right) \times ({g^{ – 1}})'(x)\) M1
\( = \frac{1}{3}{\left( {{g^{ – 1}}(x) – 1} \right)^{ – \frac{2}{3}}} \times ({g^{ – 1}})'(x)\) M1
\(h'(2) = \frac{1}{3}{\left( {{g^{ – 1}}(2) – 1} \right)^{ – \frac{2}{3}}} \times ({g^{ – 1}})'(2)\)
\( = \frac{1}{3}{(0.89605 \ldots – 1)^{ – \frac{2}{3}}} \times 0.171933 \ldots \)
\( = 0.259{\text{ }}(232 \ldots )\) A1 N4
[6 marks]
Examiners report
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
Question
A straight street of width 20 metres is bounded on its parallel sides by two vertical walls, one of height 13 metres, the other of height 8 metres. The intensity of light at point P at ground level on the street is proportional to the angle \(\theta \) where \(\theta = {\rm{A\hat PB}}\), as shown in the diagram.
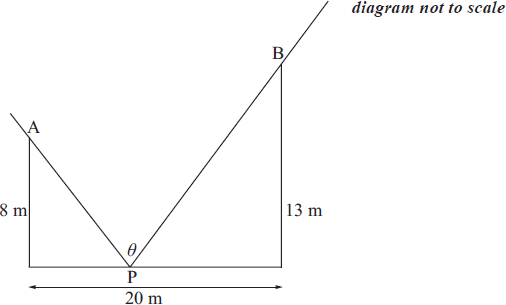
Find an expression for \(\theta \) in terms of x, where x is the distance of P from the base of the wall of height 8 m.
(i) Calculate the value of \(\theta \) when x = 0.
(ii) Calculate the value of \(\theta \) when x = 20.
Sketch the graph of \(\theta \), for \(0 \leqslant x \leqslant 20\).
Show that \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{{5(744 – 64x – {x^2})}}{{({x^2} + 64)({x^2} – 40x + 569)}}\).
Using the result in part (d), or otherwise, determine the value of x corresponding to the maximum light intensity at P. Give your answer to four significant figures.
The point P moves across the street with speed \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\). Determine the rate of change of \(\theta \) with respect to time when P is at the midpoint of the street.
Answer/Explanation
Markscheme
EITHER
\(\theta = \pi – \arctan \left( {\frac{8}{x}} \right) – \arctan \left( {\frac{{13}}{{20 – x}}} \right)\) (or equivalent) M1A1
Note: Accept \(\theta = 180^\circ – \arctan \left( {\frac{8}{x}} \right) – \arctan \left( {\frac{{13}}{{20 – x}}} \right)\) (or equivalent).
OR
\(\theta = \arctan \left( {\frac{x}{8}} \right) + \arctan \left( {\frac{{20 – x}}{{13}}} \right)\) (or equivalent) M1A1
[2 marks]
(i) \(\theta = 0.994{\text{ }}\left( { = \arctan \frac{{20}}{{13}}} \right)\) A1
(ii) \(\theta = 1.19{\text{ }}\left( { = \arctan \frac{5}{2}} \right)\) A1
[2 marks]
correct shape. A1
correct domain indicated. A1
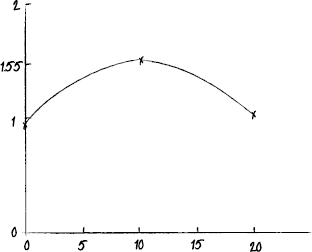
[2 marks]
attempting to differentiate one \(\arctan \left( {f(x)} \right)\) term M1
EITHER
\(\theta = \pi – \arctan \left( {\frac{8}{x}} \right) – \arctan \left( {\frac{{13}}{{20 – x}}} \right)\)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{8}{{{x^2}}} \times \frac{1}{{1 + {{\left( {\frac{8}{x}} \right)}^2}}} – \frac{{13}}{{{{(20 – x)}^2}}} \times \frac{1}{{1 + {{\left( {\frac{{13}}{{20 – x}}} \right)}^2}}}\) A1A1
OR
\(\theta = \arctan \left( {\frac{x}{8}} \right) + \arctan \left( {\frac{{20 – x}}{{13}}} \right)\)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{{\frac{1}{8}}}{{1 + {{\left( {\frac{x}{8}} \right)}^2}}} + \frac{{ – \frac{1}{{13}}}}{{1 + {{\left( {\frac{{20 – x}}{{13}}} \right)}^2}}}\) A1A1
THEN
\( = \frac{8}{{{x^2} + 64}} – \frac{{13}}{{569 – 40x + {x^2}}}\) A1
\( = \frac{{8(569 – 40x + {x^2}) – 13({x^{2}} + 64)}}{{({x^2} + 64)({x^2} – 40x + 569)}}\) M1A1
\( = \frac{{5(744 – 64x – {x^2})}}{{({x^2} + 64)({x^2} – 40x + 569)}}\) AG
[6 marks]
Maximum light intensity at P occurs when \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0\). (M1)
either attempting to solve \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0\) for x or using the graph of either \(\theta \) or \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}}\) (M1)
x = 10.05 (m) A1
[3 marks]
\(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 0.5\) (A1)
At x = 10, \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0.000453{\text{ }}\left( { = \frac{5}{{11029}}} \right)\). (A1)
use of \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}x}} \times \frac{{{\text{d}}x}}{{{\text{d}}t}}\) M1
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.000227{\text{ }}\left( { = \frac{5}{{22058}}} \right){\text{ (rad }}{{\text{s}}^{ – 1}})\) A1
Note: Award (A1) for \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = – 0.5\) and A1 for \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = – 0.000227{\text{ }}\left( { = – \frac{5}{{22058}}} \right){\text{ }}\).
Note: Implicit differentiation can be used to find \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\). Award as above.
[4 marks]
Examiners report
Part (a) was reasonably well done. While many candidates exhibited sound trigonometric knowledge to correctly express θ in terms of x, many other candidates were not able to use elementary trigonometry to formulate the required expression for θ.
In part (b), a large number of candidates did not realize that θ could only be acute and gave obtuse angle values for θ. Many candidates also demonstrated a lack of insight when substituting endpoint x-values into θ.
In part (c), many candidates sketched either inaccurate or implausible graphs.
In part (d), a large number of candidates started their differentiation incorrectly by failing to use the chain rule correctly.
For a question part situated at the end of the paper, part (e) was reasonably well done. A large number of candidates demonstrated a sound knowledge of finding where the maximum value of θ occurred and rejected solutions that were not physically feasible.
In part (f), many candidates were able to link the required rates, however only a few candidates were able to successfully apply the chain rule in a related rates context.
Question
Consider the triangle \({\text{PQR}}\) where \({\rm{Q\hat PR = 30^\circ }}\), \({\text{PQ}} = (x + 2){\text{ cm}}\) and \({\text{PR}} = {(5 – x)^2}{\text{ cm}}\), where \( – 2 < x < 5\).
Show that the area, \(A\;{\text{c}}{{\text{m}}^2}\), of the triangle is given by \(A = \frac{1}{4}({x^3} – 8{x^2} + 5x + 50)\).
(i) State \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\).
(ii) Verify that \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\).
(i) Find \(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}}\) and hence justify that \(x = \frac{1}{3}\) gives the maximum area of triangle \(PQR\).
(ii) State the maximum area of triangle \(PQR\).
(iii) Find \(QR\) when the area of triangle \(PQR\) is a maximum.
Answer/Explanation
Markscheme
use of \(A = \frac{1}{2}qr\sin \theta \) to obtain \(A = \frac{1}{2}(x + 2){(5 – x)^2}\sin 30^\circ \) M1
\( = \frac{1}{4}(x + 2)(25 – 10x + {x^2})\) A1
\(A = \frac{1}{4}({x^3} – 8{x^2} + 5x + 50)\) AG
[2 marks]
(i) \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}(3{x^2} – 16x + 5) = \frac{1}{4}(3x – 1)(x – 5)\) A1
(ii) METHOD 1
EITHER
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}\left( {3{{\left( {\frac{1}{3}} \right)}^2} – 16\left( {\frac{1}{3}} \right) + 5} \right) = 0\) M1A1
OR
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}\left( {3\left( {\frac{1}{3}} \right) – 1} \right)\left( {\left( {\frac{1}{3}} \right) – 5} \right) = 0\) M1A1
THEN
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
METHOD 2
solving \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) for \(x\) M1
\( – 2 < x < 5 \Rightarrow x = \frac{1}{3}\) A1
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
METHOD 3
a correct graph of \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\) versus \(x\) M1
the graph clearly showing that \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) A1
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
[3 marks]
(i) \(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}} = \frac{1}{2}(3x – 8)\) A1
for \(x = \frac{1}{3},{\text{ }}\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}} = – 3.5{\text{ }}( < 0)\) R1
so \(x = \frac{1}{3}\) gives the maximum area of triangle \(PQR\) AG
(ii) \({A_{\max }} = \frac{{343}}{{27}}{\text{ }}( = 12.7){\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
(iii) \({\text{PQ}} = \frac{7}{3}{\text{ (cm)}}\) and \({\text{PR}} = {\left( {\frac{{14}}{3}} \right)^2}{\text{ (cm)}}\) (A1)
\({\text{Q}}{{\text{R}}^2} = {\left( {\frac{7}{3}} \right)^2} + {\left( {\frac{{14}}{3}} \right)^4} – 2\left( {\frac{7}{3}} \right){\left( {\frac{{14}}{3}} \right)^2}\cos 30^\circ \) (M1)(A1)
\( = 391.702 \ldots \)
\({\text{QR = 19.8 (cm)}}\) A1
[7 marks]
Total [12 marks]
Examiners report
This question was generally well done. Parts (a) and (b) were straightforward and well answered.
This question was generally well done. Parts (a) and (b) were straightforward and well answered.
This question was generally well done. Parts (c) (i) and (ii) were also well answered with most candidates correctly applying the second derivative test and displaying sound reasoning skills.
Part (c) (iii) required the use of the cosine rule and was reasonably well done. The most common error committed by candidates in attempting to find the value of \(QR\) was to use \({\text{PR}} = \frac{{14}}{3}{\text{ (cm)}}\) rather than \({\text{PR}} = {\left( {\frac{{14}}{3}} \right)^2}{\text{ (cm)}}\). The occasional candidate used \(\cos 30^\circ = \frac{1}{2}\).
Question
A function \(f\) is defined by \(f(x) = {x^3} + {{\text{e}}^x} + 1,{\text{ }}x \in \mathbb{R}\). By considering \(f'(x)\) determine whether \(f\) is a one-to-one or a many-to-one function.
Answer/Explanation
Markscheme
\(f'(x) = 3{x^2} + {{\text{e}}^x}\) A1
Note: Accept labelled diagram showing the graph \(y = f'(x)\) above the x-axis;
do not accept unlabelled graphs nor graph of \(y = f(x)\).
EITHER
this is always \( > 0\) R1
so the function is (strictly) increasing R1
and thus \(1 – 1\) A1
OR
this is always \( > 0\;\;\;{\text{(accept }} \ne 0{\text{)}}\) R1
so there are no turning points R1
and thus \(1 – 1\) A1
Note: A1 is dependent on the first R1.
[4 marks]
Examiners report
The differentiation was normally completed correctly, but then a large number did not realise what was required to determine the type of the original function. Most candidates scored 1/4 and wrote explanations that showed little or no understanding of the relation between first derivative and the given function. For example, it was common to see comments about horizontal and vertical line tests but applied to the incorrect function.In term of mathematical language, it was noted that candidates used many terms incorrectly showing no knowledge of the meaning of terms like ‘parabola’, ‘even’ or ‘odd’ ( or no idea about these concepts).
Question
The function f is defined on the domain [0, 2] by \(f(x) = \ln (x + 1)\sin (\pi x)\) .
Obtain an expression for \(f'(x)\) .
Sketch the graphs of f and \(f’\) on the same axes, showing clearly all x-intercepts.
Find the x-coordinates of the two points of inflexion on the graph of f .
Find the equation of the normal to the graph of f where x = 0.75 , giving your answer in the form y = mx + c .
Consider the points \({\text{A}}\left( {a{\text{ }},{\text{ }}f(a)} \right)\) , \({\text{B}}\left( {b{\text{ }},{\text{ }}f(b)} \right)\) and \({\text{C}}\left( {c{\text{ }},{\text{ }}f(c)} \right)\) where a , b and c \((a < b < c)\) are the solutions of the equation \(f(x) = f'(x)\) . Find the area of the triangle ABC.
Answer/Explanation
Markscheme
\(f'(x) = \frac{1}{{x + 1}}\sin (\pi x) + \pi \ln (x + 1)\cos (\pi x)\) M1A1A1
[3 marks]
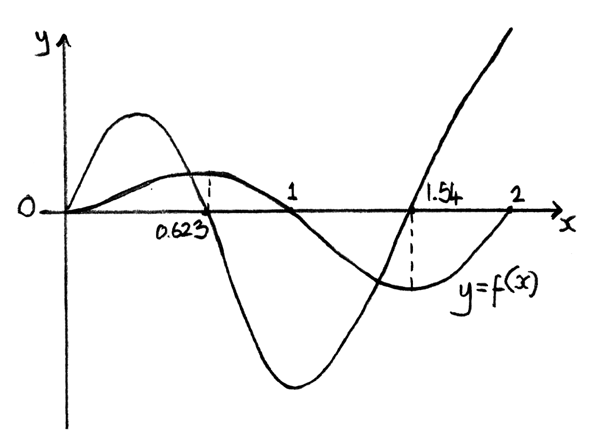 A4
A4
Note: Award A1A1 for graphs, A1A1 for intercepts.
[4 marks]
0.310, 1.12 A1A1
[2 marks]
\(f'(0.75) = – 0.839092\) A1
so equation of normal is \(y – 0.39570812 = \frac{1}{{0.839092}}(x – 0.75)\) M1
\(y = 1.19x – 0.498\) A1
[3 marks]
\({\text{A}}(0,{\text{ }}0)\)
\({\text{B(}}\overbrace {0.548 \ldots }^c,\overbrace {0.432 \ldots }^d)\) A1
\({\text{C(}}\overbrace {1.44 \ldots }^e,\overbrace { – 0.881 \ldots }^f)\) A1
Note: Accept coordinates for B and C rounded to 3 significant figures.
area \(\Delta {\text{ABC}} = \frac{1}{2}|\)(ci + dj) \( \times \) (ei + fj)\(|\) M1A1
\( = \frac{1}{2}(de – cf)\) A1
\( = 0.554\) A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
