Question
The diagram shows the plan of an art gallery a metres wide. [AB] represents a doorway, leading to an exit corridor b metres wide. In order to remove a painting from the art gallery, CD (denoted by L ) is measured for various values of \(\alpha \) , as represented in the diagram.
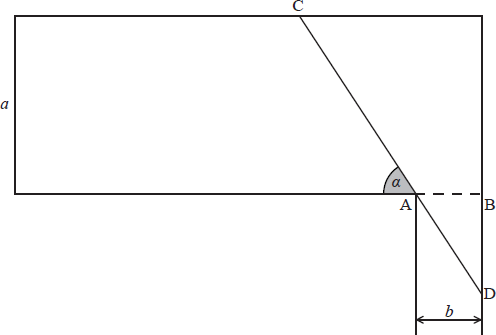
If \(\alpha \) is the angle between [CD] and the wall, show that \(L = \frac{a }{{\sin \alpha }} + \frac{b}{{\cos \alpha }}{\text{, }}0 < \alpha < \frac{\pi }{2}\).
If a = 5 and b = 1, find the maximum length of a painting that can be removed through this doorway.
Let a = 3k and b = k .
Find \(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }}\).
Let a = 3k and b = k .
Find, in terms of k , the maximum length of a painting that can be removed from the gallery through this doorway.
Let a = 3k and b = k .
Find the minimum value of k if a painting 8 metres long is to be removed through this doorway.
Answer/Explanation
Markscheme
\(L = {\text{CA}} + {\text{AD}}\) M1
\({\text{sin}}\alpha {\text{ = }}\frac{a}{{{\text{CA}}}} \Rightarrow {\text{CA}} = \frac{a}{{\sin \alpha }}\) A1
\(\cos \alpha = \frac{b}{{{\text{AD}}}} \Rightarrow {\text{AD}} = \frac{b}{{\cos \alpha }}\) A1
\(L = \frac{a}{{\sin \alpha }} + \frac{b}{{\cos \alpha }}\) AG
[2 marks]
\(a = 5{\text{ and }}b = 1 \Rightarrow L = \frac{5}{{\sin \alpha }} + \frac{1}{{\cos \alpha }}\)
METHOD 1
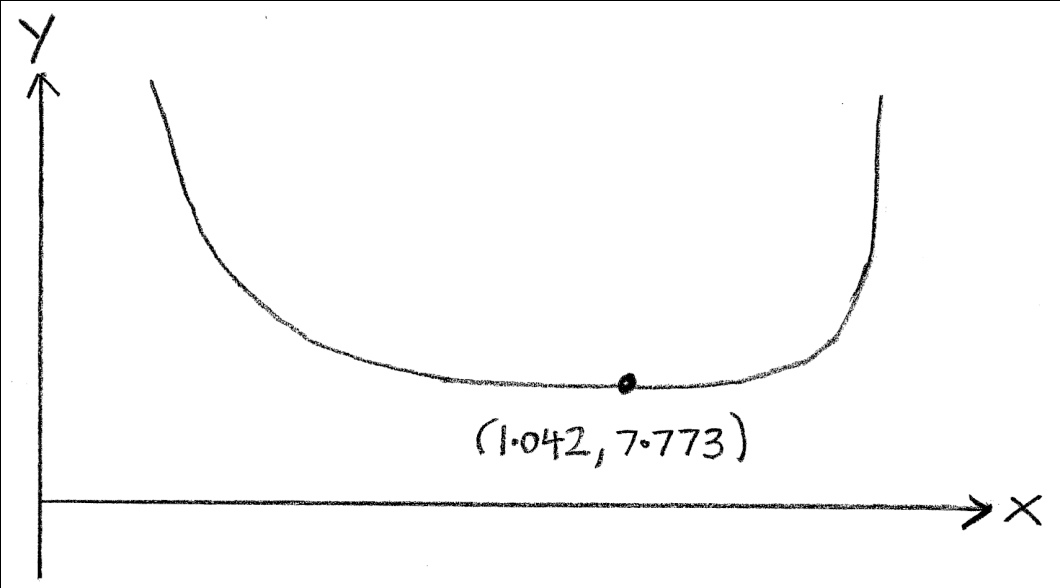 (M1)
(M1)
minimum from graph \( \Rightarrow L = 7.77\) (M1)A1
minimum of L gives the max length of the painting R1
[4 marks]
METHOD 2
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 5\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{\sin \alpha }}{{{{\cos }^2}\alpha }}\) (M1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = 5 \Rightarrow \tan \alpha = \sqrt[{3{\text{ }}}]{5}{\text{ }}(\alpha = 1.0416…)\) (M1)
minimum of L gives the max length of the painting R1
maximum length = 7.77 A1
[4 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k\cos \alpha }}{{{{\sin }^2}\alpha }} + \frac{{k\sin \alpha }}{{{{\cos }^2}\alpha }}\,\,\,\,\,{\text{(or equivalent)}}\) M1A1A1
[3 marks]
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = \frac{{ – 3k{{\cos }^3}\alpha + k{{\sin }^3}\alpha }}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }}\) (A1)
\(\frac{{{\text{d}}L}}{{{\text{d}}\alpha }} = 0 \Rightarrow \frac{{{{\sin }^3}\alpha }}{{{{\cos }^3}\alpha }} = \frac{{3k}}{k} \Rightarrow \tan \alpha = \sqrt[3]{3}\,\,\,\,\,(\alpha = 0.96454…)\) M1A1
\(\tan \alpha = \sqrt[3]{3} \Rightarrow \frac{1}{{\cos \alpha }} = \sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(1.755…)\) (A1)
\({\text{and }}\frac{1}{{\sin \alpha }} = \frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}\,\,\,\,\,(1.216…)\) (A1)
\(L = 3k\left( {\frac{{\sqrt {1 + \sqrt[3]{9}} }}{{\sqrt[3]{3}}}} \right) + k\sqrt {1 + \sqrt[3]{9}} \,\,\,\,\,(L = 5.405598…k)\) A1 N4
[6 marks]
\(L \leqslant 8 \Rightarrow k \geqslant 1.48\) M1A1
the minimum value is 1.48
[2 marks]
Examiners report
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Part (a) was very well done by most candidates. Parts (b), (c) and (d) required a subtle balance between abstraction, differentiation skills and use of GDC.
In part (b), although candidates were asked to justify their reasoning, very few candidates offered an explanation for the maximum. Therefore most candidates did not earn the R1 mark in part (b). Also not as many candidates as anticipated used a graphical approach, preferring to use the calculus with varying degrees of success. In part (c), some candidates calculated the derivatives of inverse trigonometric functions. Some candidates had difficulty with parts (d) and (e). In part (d), some candidates erroneously used their alpha value from part (b). In part (d) many candidates used GDC to calculate decimal values for \(\alpha \) and L. The premature rounding of decimals led sometimes to inaccurate results. Nevertheless many candidates got excellent results in this question.
Question
Consider the triangle \({\text{PQR}}\) where \({\rm{Q\hat PR = 30^\circ }}\), \({\text{PQ}} = (x + 2){\text{ cm}}\) and \({\text{PR}} = {(5 – x)^2}{\text{ cm}}\), where \( – 2 < x < 5\).
Show that the area, \(A\;{\text{c}}{{\text{m}}^2}\), of the triangle is given by \(A = \frac{1}{4}({x^3} – 8{x^2} + 5x + 50)\).
(i) State \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\).
(ii) Verify that \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\).
(i) Find \(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}}\) and hence justify that \(x = \frac{1}{3}\) gives the maximum area of triangle \(PQR\).
(ii) State the maximum area of triangle \(PQR\).
(iii) Find \(QR\) when the area of triangle \(PQR\) is a maximum.
Answer/Explanation
Markscheme
use of \(A = \frac{1}{2}qr\sin \theta \) to obtain \(A = \frac{1}{2}(x + 2){(5 – x)^2}\sin 30^\circ \) M1
\( = \frac{1}{4}(x + 2)(25 – 10x + {x^2})\) A1
\(A = \frac{1}{4}({x^3} – 8{x^2} + 5x + 50)\) AG
[2 marks]
(i) \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}(3{x^2} – 16x + 5) = \frac{1}{4}(3x – 1)(x – 5)\) A1
(ii) METHOD 1
EITHER
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}\left( {3{{\left( {\frac{1}{3}} \right)}^2} – 16\left( {\frac{1}{3}} \right) + 5} \right) = 0\) M1A1
OR
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = \frac{1}{4}\left( {3\left( {\frac{1}{3}} \right) – 1} \right)\left( {\left( {\frac{1}{3}} \right) – 5} \right) = 0\) M1A1
THEN
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
METHOD 2
solving \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) for \(x\) M1
\( – 2 < x < 5 \Rightarrow x = \frac{1}{3}\) A1
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
METHOD 3
a correct graph of \(\frac{{{\text{d}}A}}{{{\text{d}}x}}\) versus \(x\) M1
the graph clearly showing that \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) A1
so \(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0\) when \(x = \frac{1}{3}\) AG
[3 marks]
(i) \(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}} = \frac{1}{2}(3x – 8)\) A1
for \(x = \frac{1}{3},{\text{ }}\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}} = – 3.5{\text{ }}( < 0)\) R1
so \(x = \frac{1}{3}\) gives the maximum area of triangle \(PQR\) AG
(ii) \({A_{\max }} = \frac{{343}}{{27}}{\text{ }}( = 12.7){\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
(iii) \({\text{PQ}} = \frac{7}{3}{\text{ (cm)}}\) and \({\text{PR}} = {\left( {\frac{{14}}{3}} \right)^2}{\text{ (cm)}}\) (A1)
\({\text{Q}}{{\text{R}}^2} = {\left( {\frac{7}{3}} \right)^2} + {\left( {\frac{{14}}{3}} \right)^4} – 2\left( {\frac{7}{3}} \right){\left( {\frac{{14}}{3}} \right)^2}\cos 30^\circ \) (M1)(A1)
\( = 391.702 \ldots \)
\({\text{QR = 19.8 (cm)}}\) A1
[7 marks]
Total [12 marks]
Examiners report
This question was generally well done. Parts (a) and (b) were straightforward and well answered.
This question was generally well done. Parts (a) and (b) were straightforward and well answered.
This question was generally well done. Parts (c) (i) and (ii) were also well answered with most candidates correctly applying the second derivative test and displaying sound reasoning skills.
Part (c) (iii) required the use of the cosine rule and was reasonably well done. The most common error committed by candidates in attempting to find the value of \(QR\) was to use \({\text{PR}} = \frac{{14}}{3}{\text{ (cm)}}\) rather than \({\text{PR}} = {\left( {\frac{{14}}{3}} \right)^2}{\text{ (cm)}}\). The occasional candidate used \(\cos 30^\circ = \frac{1}{2}\).
