Question
Consider the curve defined by the equation \({x^2} + \sin y – xy = 0\) .
Find the gradient of the tangent to the curve at the point \((\pi ,{\text{ }}\pi )\) .
Hence, show that \(\tan \theta = \frac{1}{{1 + 2\pi }}\), where \(\theta \) is the acute angle between the tangent to the curve at \((\pi ,{\text{ }}\pi )\) and the line y = x .
Answer/Explanation
Markscheme
attempt to differentiate implicitly M1
\(2x + \cos y\frac{{{\text{d}}y}}{{{\text{d}}x}} – y – x\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) A1A1
Note: A1 for differentiating \({x^2}\) and sin y ; A1 for differentiating xy.
substitute x and y by \(\pi \) M1
\(2\pi – \frac{{{\text{d}}y}}{{{\text{d}}x}} – \pi – \pi \frac{{{\text{d}}y}}{{{\text{d}}x}} = 0 \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{\pi }{{1 + \pi }}\) M1A1
Note: M1 for attempt to make dy/dx the subject. This could be seen earlier.
[6 marks]
\(\theta = \frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}\) (or seen the other way) M1
\(\tan \theta = \tan \left( {\frac{\pi }{4} – \arctan \frac{\pi }{{1 + \pi }}} \right) = \frac{{1 – \frac{\pi }{{1 + \pi }}}}{{1 + \frac{\pi }{{1 + \pi }}}}\) M1A1
\(\tan \theta = \frac{1}{{1 + 2\pi }}\) AG
[3 marks]
Examiners report
Part a) proved an easy 6 marks for most candidates, while the majority failed to make any headway with part b), with some attempting to find the equation of their line in the form y = mx + c . Only the best candidates were able to see their way through to the given answer.
Part a) proved an easy 6 marks for most candidates, while the majority failed to make any headway with part b), with some attempting to find the equation of their line in the form y = mx + c . Only the best candidates were able to see their way through to the given answer.
Question
A curve has equation \(\arctan {x^2} + \arctan {y^2} = \frac{\pi }{4}\).
(a) Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) in terms of x and y.
(b) Find the gradient of the curve at the point where \(x = \frac{1}{{\sqrt 2 }}\) and \(y < 0\).
Answer/Explanation
Markscheme
(a) METHOD 1
\(\frac{{2x}}{{1 + {x^4}}} + \frac{{2y}}{{1 + {y^4}}}\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) M1A1A1
Note: Award M1 for implicit differentiation, A1 for LHS and A1 for RHS.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{x\left( {1 + {y^4}} \right)}}{{y\left( {1 + {x^4}} \right)}}\) A1
METHOD 2
\({y^2} = \tan \left( {\frac{\pi }{4} – \arctan {x^2}} \right)\)
\( = \frac{{\tan \frac{\pi }{4} – \tan \left( {\arctan {x^2}} \right)}}{{1 + \left( {\tan \frac{\pi }{4}} \right)\left( {\tan \left( {\arctan {x^2}} \right)} \right)}}\) (M1)
\( = \frac{{1 – {x^2}}}{{1 + {x^2}}}\) A1
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 2x\left( {1 + {x^2}} \right) – 2x\left( {1 – {x^2}} \right)}}{{{{\left( {1 + {x^2}} \right)}^2}}}\) M1
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 4x}}{{{{\left( {1 + {x^2}} \right)}^2}}}\)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2x}}{{y{{\left( {1 + {x^2}} \right)}^2}}}\) A1
\(\left( { = \frac{{2x\sqrt {1 + {x^2}} }}{{\sqrt {1 – {x^2}} {{\left( {1 + {x^2}} \right)}^2}}}} \right)\)
[4 marks]
(b) \({y^2} = \tan \left( {\frac{\pi }{4} – \arctan \frac{1}{2}} \right)\) (M1)
\( = \frac{{\tan \frac{\pi }{4} – \tan \left( {\arctan \frac{1}{2}} \right)}}{{1 + \left( {\tan \frac{\pi }{4}} \right)\left( {\tan \left( {\arctan \frac{1}{2}} \right)} \right)}}\) (M1)
Note: The two M1s may be awarded for working in part (a).
\( = \frac{{1 – \frac{1}{2}}}{{1 + \frac{1}{2}}} = \frac{1}{3}\) A1
\(y = – \frac{1}{{\sqrt 3 }}\) A1
substitution into \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\)
\( = \frac{{4\sqrt 6 }}{9}\) A1
Note: Accept \(\frac{{8\sqrt 3 }}{{9\sqrt 2 }}\) etc.
[5 marks]
Total [9 marks]
Examiners report
Question
Consider two functions \(f\) and \(g\) and their derivatives \(f’\) and \(g’\). The following table shows the values for the two functions and their derivatives at \(x = 1\), \(2\) and \(3\).
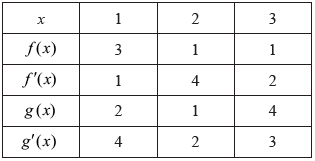
Given that \(p(x) = f(x)g(x)\) and \(h(x) = g \circ f(x)\), find
\(p'(3)\);
\(h'(2)\).
Answer/Explanation
Markscheme
\(p'(3) = f'(3)g(3) + g'(3)f(3)\) (M1)
Note: Award M1 if the derivative is in terms of \(x\) or \(3\).
\( = 2 \times 4 + 3 \times 1\)
\( = 11\) A1
[2 marks]
\(h'(x) = g’\left( {f(x)} \right)f'(x)\) (M1)(A1)
\(h'(2) = g'(1)f'(2)\) A1
\( = 4 \times 4\)
\( = 16\) A1
[4 marks]
Total [6 marks]
Examiners report
This was a problem question for many candidates. Some quite strong candidates, on the evidence of their performance on other questions, did not realise that ‘composite functions’ and ‘functions of a function’ were the same thing, and therefore that the chain rule applied.
This was a problem question for many candidates. Some quite strong candidates, on the evidence of their performance on other questions, did not realise that ‘composite functions’ and ‘functions of a function’ were the same thing, and therefore that the chain rule applied.
Question
Let \(y(x) = x{e^{3x}},{\text{ }}x \in \mathbb{R}\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Prove by induction that \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n – 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\) for \(n \in {\mathbb{Z}^ + }\).
Find the coordinates of any local maximum and minimum points on the graph of \(y(x)\).
Justify whether any such point is a maximum or a minimum.
Find the coordinates of any points of inflexion on the graph of \(y(x)\). Justify whether any such point is a point of inflexion.
Hence sketch the graph of \(y(x)\), indicating clearly the points found in parts (c) and (d) and any intercepts with the axes.
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = ({{\text{e}}^{3x}} + 3x{{\text{e}}^{3x}})\) M1A1
[2 marks]
let \(P(n)\) be the statement \(\frac{{{{\text{d}}^n}y}}{{{\text{d}}{x^n}}} = n{3^{n – 1}}{{\text{e}}^{3x}} + x{3^n}{{\text{e}}^{3x}}\)
prove for \(n = 1\) M1
\(LHS\) of \(P(1)\) is \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) which is \(1 \times {{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}}\) and \(RHS\) is \({3^0}{{\text{e}}^{3x}} + x{3^1}{{\text{e}}^{3x}}\) R1
as \({\text{LHS}} = {\text{RHS, }}P(1)\) is true
assume \(P(k)\) is true and attempt to prove \(P(k + 1)\) is true M1
assuming \(\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}} = k{3^{k – 1}}{{\text{e}}^{3x}} + x{3^k}{{\text{e}}^{3x}}\)
\(\frac{{{{\text{d}}^{k + 1}}y}}{{{\text{d}}{x^{k + 1}}}} = \frac{{\text{d}}}{{{\text{d}}x}}\left( {\frac{{{{\text{d}}^k}y}}{{{\text{d}}{x^k}}}} \right)\) (M1)
\( = k{3^{k – 1}} \times 3{{\text{e}}^{3x}} + 1 \times {3^k}{{\text{e}}^{3x}} + x{3^k} \times 3{{\text{e}}^{3x}}\) A1
\( = (k + 1){3^k}{{\text{e}}^{3x}} + x{3^{k + 1}}{{\text{e}}^{3x}}\;\;\;\)(as required) A1
Note: Can award the A marks independent of the M marks
since \(P(1)\) is true and \(P(k)\) is true \( \Rightarrow P(k + 1)\) is true
then (by \(PMI\)), \(P(n)\) is true \((\forall n \in {\mathbb{Z}^ + })\) R1
Note: To gain last R1 at least four of the above marks must have been gained.
[7 marks]
\({{\text{e}}^{3x}} + x \times 3{{\text{e}}^{3x}} = 0 \Rightarrow 1 + 3x = 0 \Rightarrow x = – \frac{1}{3}\) M1A1
point is \(\left( { – \frac{1}{3},{\text{ }} – \frac{1}{{3{\text{e}}}}} \right)\) A1
EITHER
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\)
when \(x = – \frac{1}{3},{\text{ }}\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} > 0\) therefore the point is a minimum M1A1
OR

nature table shows point is a minimum M1A1
[5 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}}\) A1
\(2 \times 3{{\text{e}}^{3x}} + x \times {3^2}{{\text{e}}^{3x}} = 0 \Rightarrow 2 + 3x = 0 \Rightarrow x = – \frac{2}{3}\) M1A1
point is \(\left( { – \frac{2}{3},{\text{ }} – \frac{2}{{3{{\text{e}}^2}}}} \right)\) A1

since the curvature does change (concave down to concave up) it is a point of inflection R1
Note: Allow \({3^{{\text{rd}}}}\) derivative is not zero at \( – \frac{2}{3}\)
[5 marks]
(general shape including asymptote and through origin) A1
showing minimum and point of inflection A1
Note: Only indication of position of answers to (c) and (d) required, not coordinates.
[2 marks]
Total [21 marks]
Examiners report
Well done.
The logic of an induction proof was not known well enough. Many candidates used what they had to prove rather than differentiating what they had assumed. They did not have enough experience in doing Induction proofs.
Good, some forgot to test for min/max, some forgot to give the \(y\) value.
Again quite good, some forgot to check for change in curvature and some forgot the \(y\) value.
Some accurate sketches, some had all the information from earlier parts but could not apply it. The asymptote was often missed.
Question
Consider the curve \(y = \frac{1}{{1 – x}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 1\).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Determine the equation of the normal to the curve at the point \(x = 3\) in the form \(ax + by + c = 0\) where \(a,{\text{ }}b,{\text{ }}c \in \mathbb{Z}\).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {(1 – x)^{ – 2}}\;\;\;\left( { = \frac{1}{{{{(1 – x)}^2}}}} \right)\) (M1)A1
[2 marks]
gradient of Tangent \( = \frac{1}{4}\) (A1)
gradient of Normal \( = – 4\) (M1)
\(y + \frac{1}{2} = – 4(x – 3)\) or attempt to find \(c\) in \(y = mx + c\) M1
\(8x + 2y – 23 = 0\) A1
[4 marks]
Total [6 marks]
Examiners report
[N/A]
[N/A]
Question
Consider the function defined by \(f(x) = x\sqrt {1 – {x^2}} \) on the domain \( – 1 \le x \le 1\).
Show that \(f\) is an odd function.
Find \(f'(x)\).
Hence find the \(x\)-coordinates of any local maximum or minimum points.
Find the range of \(f\).
Sketch the graph of \(y = f(x)\) indicating clearly the coordinates of the \(x\)-intercepts and any local maximum or minimum points.
Find the area of the region enclosed by the graph of \(y = f(x)\) and the \(x\)-axis for \(x \ge 0\).
Show that \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \).
Answer/Explanation
Markscheme
\(f( – x) = ( – x)\sqrt {1 – {{( – x)}^2}} \) M1
\( = – x\sqrt {1 – {x^2}} \)
\( = – f(x)\) R1
hence \(f\) is odd AG
[2 marks]
\(f'(x) = x \bullet \frac{1}{2}{(1 – {x^2})^{ – \frac{1}{2}}} \bullet – 2x + {(1 – {x^2})^{\frac{1}{2}}}\) M1A1A1
[3 marks]
\(f'(x) = \sqrt {1 – {x^2}} – \frac{{{x^2}}}{{\sqrt {1 – {x^2}} }}\;\;\;\left( { = \frac{{1 – 2{x^2}}}{{\sqrt {1 – {x^2}} }}} \right)\) A1
Note: This may be seen in part (b).
Note: Do not allow FT from part (b).
\(f'(x) = 0 \Rightarrow 1 – 2{x^2} = 0\) M1
\(x = \pm \frac{1}{{\sqrt 2 }}\) A1
[3 marks]
\(y\)-coordinates of the Max Min Points are \(y = \pm \frac{1}{2}\) M1A1
so range of \(f(x)\) is \(\left[ { – \frac{1}{2},{\text{ }}\frac{1}{2}} \right]\) A1
Note: Allow FT from (c) if values of \(x\), within the domain, are used.
[3 marks]
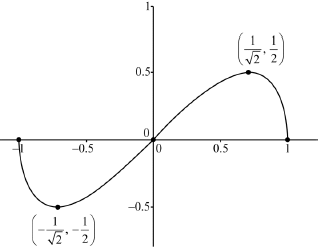
Shape: The graph of an odd function, on the given domain, s-shaped,
where the max(min) is the right(left) of \(0.5{\text{ }}( – 0.5)\) A1
\(x\)-intercepts A1
turning points A1
[3 marks]
\({\text{area}} = \int_0^1 {x\sqrt {1 – {x^2}} {\text{d}}x} \) (M1)
attempt at “backwards chain rule” or substitution M1
\( = – \frac{1}{2}\int_0^1 {( – 2x)\sqrt {1 – {x^2}} {\text{d}}x} \)
Note: Condone absence of limits for first two marks.
\( = \left[ {\frac{2}{3}{{(1 – {x^2})}^{\frac{3}{2}}} \bullet – \frac{1}{2}} \right]_0^1\) A1
\( = \left[ { – \frac{1}{3}{{(1 – {x^2})}^{\frac{3}{2}}}} \right]_0^1\)
\( = 0 – \left( { – \frac{1}{3}} \right) = \frac{1}{3}\) A1
[4 marks]
\(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > 0} \) R1
\(\left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right| = 0\) R1
so \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \) AG
[2 marks]
Total [20 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
A curve is given by the equation \(y = \sin (\pi \cos x)\).
Find the coordinates of all the points on the curve for which \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0,{\text{ }}0 \leqslant x \leqslant \pi \).
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \cos (\pi \cos x) \times \pi \sin x\) M1A1
Note: Award follow through marks below if their answer is a multiple of the correct answer.
considering either \(\sin x = 0\) or \(\cos (\pi \cos x) = 0\) (M1)
\(x = 0,{\text{ }}\pi \) A1
\(\pi \cos x = \frac{\pi }{2},{\text{ }} – \frac{\pi }{2}{\text{ }}\left( { \Rightarrow \cos x = \frac{1}{2}, – \frac{1}{2}} \right)\) M1
Note: Condone absence of \( – \frac{\pi }{2}\).
\( \Rightarrow x = \frac{\pi }{3},{\text{ }}\frac{{2\pi }}{3}\)
\((0,{\text{ }}0),{\text{ }}\left( {\frac{\pi }{3},{\text{ 1}}} \right),{\text{ (}}\pi {\text{, 0)}}\) A1
\(\left( {\frac{{2\pi }}{3},{\text{ }} – 1} \right)\) A1
[7 marks]
Examiners report
This was not a straight-forward differentiation and it was pleasing to see how many candidates managed to do it correctly. Having done this they found two of the solutions, often three of the solutions, successfully. The final solution was found by only a few candidates. Again candidates lost marks unnecessarily by not close reading the question and realising that they needed both coordinates of the points, not just the \(x\)-coordinates.
Question
The following graph shows the relation \(x = 3\cos 2y + 4,{\text{ }}0 \leqslant y \leqslant \pi \).
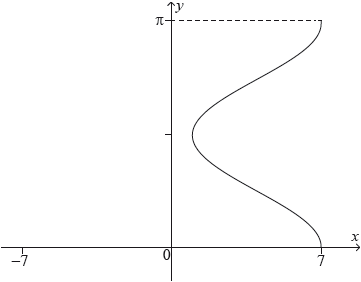
The curve is rotated 360° about the \(y\)-axis to form a volume of revolution.
A container with this shape is made with a solid base of diameter 14 cm . The container is filled with water at a rate of \({\text{2 c}}{{\text{m}}^{\text{3}}}\,{\text{mi}}{{\text{n}}^{ – 1}}\). At time \(t\) minutes, the water depth is \(h{\text{ cm, }}0 \leqslant h \leqslant \pi \) and the volume of water in the container is \(V{\text{ c}}{{\text{m}}^{\text{3}}}\).
Calculate the value of the volume generated.
(i) Given that \(\frac{{{\text{d}}V}}{{{\text{d}}h}} = \pi {(3\cos 2h + 4)^2}\), find an expression for \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\).
(ii) Find the value of \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) when \(h = \frac{\pi }{4}\).
(i) Find \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(ii) Find the values of \(h\) for which \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = 0\).
(iii) By making specific reference to the shape of the container, interpret \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) at the values of \(h\) found in part (c)(ii).
Answer/Explanation
Markscheme
use of \(\pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
Note: Condone any or missing limits.
\(V = \pi \int_0^\pi {{{(3\cos 2y + 4)}^2}{\text{d}}y} \) (A1)
\( = \pi \int_0^\pi {(9{{\cos }^2}2y + 24\cos 2y + 16){\text{d}}y} \) A1
\(9{\cos ^2}2y = \frac{9}{2}(1 + \cos 4y)\) (M1)
\( = \pi \left[ {\frac{{9y}}{2} + \frac{9}{8}\sin 4y + 12\sin 2y + 16y} \right]_0^\pi \) M1A1
\( = \pi \left( {\frac{{9\pi }}{2} + 16\pi } \right)\) (A1)
\( = \frac{{41{\pi ^2}}}{2}{\text{ (c}}{{\text{m}}^3})\) A1
Note: If the coefficient “\(\pi \)” is absent, or eg, “\(2\pi \)” is used, only M marks are available.
[8 marks]
(i) attempting to use \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}V}}{{{\text{d}}t}} \times \frac{{{\text{d}}h}}{{{\text{d}}V}}\) with \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 2\) M1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}}\) A1
(ii) substituting \(h = \frac{\pi }{4}\) into \(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{8\pi }}{\text{ (cm}}\,{\text{mi}}{{\text{n}}^{ – 1}})\) A1
Note: Do not allow FT marks for (b)(ii).
[4 marks]
(i) \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}} = \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right) = \frac{{{\text{d}}h}}{{{\text{d}}t}} \times \frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\) (M1)
\( = \frac{2}{{\pi {{(3\cos 2h + 4)}^2}}} \times \frac{{24\sin 2h}}{{\pi {{(3\cos 2h + 4)}^3}}}\) M1A1
Note: Award M1 for attempting to find \(\frac{{\text{d}}}{{{\text{d}}h}}\left( {\frac{{{\text{d}}h}}{{{\text{d}}t}}} \right)\).
\( = \frac{{48\sin 2h}}{{{\pi ^2}{{(3\cos 2h + 4)}^5}}}\) A1
(ii) \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) A1
Note: Award A1 for \(\sin 2h = 0 \Rightarrow h = 0,{\text{ }}\frac{\pi }{2},{\text{ }}\pi \) from an incorrect \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
(iii) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a minimum at \(h = 0,{\text{ }}\pi \) and the container is widest at these values R1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}}\) is a maximum at \(h = \frac{\pi }{2}\) and the container is narrowest at this value R1
[7 marks]
Examiners report
Part (a) was often answered well, though for some reason a minority tended to use the incorrect \(\pi \int {{{(3\cos 2y)}^2}{\text{d}}y} \) and gained few marks thereafter. Incorrect limits were sometimes seen, which led to only method marks being available. A pleasing number were able to deal with the integration of \({\cos ^2}2y\) through the use of the correct identity.
Part (b) was well answered and did not pose too many problems.
Correct answers to part (c) were rarely seen. Only the very best candidates appreciated the correct use of the chain rule when trying to determine an expression for \(\frac{{{{\text{d}}^2}h}}{{{\text{d}}{t^2}}}\).
Question
Let \(y = {\text{si}}{{\text{n}}^2}\theta ,\,\,0 \leqslant \theta \leqslant \pi \).
Find \(\frac{{{\text{d}}y}}{{{\text{d}}\theta }}\)
Hence find the values of θ for which \(\frac{{{\text{d}}y}}{{{\text{d}}\theta }} = 2y\).
Answer/Explanation
Markscheme
attempt at chain rule or product rule (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}\theta }} = 2\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta \) A1
[2 marks]
\(2\,{\text{sin}}\,\theta \,{\text{cos}}\,\theta = 2{\text{si}}{{\text{n}}^2}\theta \)
sin θ = 0 (A1)
θ = 0, \(\pi \) A1
obtaining cos θ = sin θ (M1)
tan θ = 1 (M1)
\(\theta = \frac{\pi }{4}\) A1
[5 marks]
Examiners report
[N/A]
[N/A]
Question
Let \(y = {\text{arccos}}\left( {\frac{x}{2}} \right)\)
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Find \(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} \).
Answer/Explanation
Markscheme
\(y = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{{2\sqrt {1 – {{\left( {\frac{x}{2}} \right)}^2}} }}\left( { = – \frac{1}{{\sqrt {4 – {x^2}} }}} \right)\) M1A1
Note: M1 is for use of the chain rule.
[2 marks]
attempt at integration by parts M1
\(u = {\text{arccos}}\left( {\frac{x}{2}} \right) \Rightarrow \frac{{{\text{d}}u}}{{{\text{d}}x}} = – \frac{1}{{\sqrt {4 – {x^2}} }}\)
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 1 \Rightarrow v = x\) (A1)
\(\int_0^1 {{\text{arccos}}\left( {\frac{x}{2}} \right){\text{d}}x} = \left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \int_0^1 {\frac{1}{{\sqrt {4 – {x^2}} }}} dx\) A1
using integration by substitution or inspection (M1)
\(\left[ {x\,\,{\text{arccos}}\left( {\frac{x}{2}} \right)} \right]_0^1 + \left[ { – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}} \right]_0^1\) A1
Note: Award A1 for \({ – {{\left( {4 – {x^2}} \right)}^{\frac{1}{2}}}}\) or equivalent.
Note: Condone lack of limits to this point.
attempt to substitute limits into their integral M1
\( = \frac{\pi }{3} – \sqrt 3 + 2\) A1
[7 marks]
Examiners report
[N/A]
[N/A]
Question
Consider the functions \(f,\,\,g,\) defined for \(x \in \mathbb{R}\), given by \(f\left( x \right) = {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) and \(g\left( x \right) = {{\text{e}}^{ – x}}\,{\text{cos}}\,x\).
Find \(f’\left( x \right)\).
Find \(g’\left( x \right)\).
Hence, or otherwise, find \(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} \).
Answer/Explanation
Markscheme
attempt at product rule M1
\(f’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + {{\text{e}}^{ – x}}\,{\text{cos}}\,x\) A1
[2 marks]
\(g’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
[1 mark]
METHOD 1
Attempt to add \(f’\left( x \right)\) and \(g’\left( x \right)\) (M1)
\(f’\left( x \right) + g’\left( x \right) = – 2{{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
\(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} = \left[ { – \frac{{{{\text{e}}^{ – x}}}}{2}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)} \right]_0^\pi \) (or equivalent) A1
Note: Condone absence of limits.
\( = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)\) A1
METHOD 2
\(I = \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\( = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) OR \( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) M1A1
\( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\(I = \frac{1}{2}{{\text{e}}^{ – x}}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)\) A1
\(\int_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)} \) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]