Question
If \(y = \ln \left( {\frac{1}{3}(1 + {{\text{e}}^{ – 2x}})} \right)\), show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{2}{3}({{\text{e}}^{ – y}} – 3)\) .
Answer/Explanation
Markscheme
\(y = \ln \left( {\frac{1}{3}(1 + {{\text{e}}^{ – 2x}})} \right)\)
EITHER
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – \frac{2}{3}{{\text{e}}^{ – 2x}}}}{{\frac{1}{3}(1 + {{\text{e}}^{ – 2x}})}}\) M1A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 2{{\text{e}}^{ – 2x}}}}{{1 + {{\text{e}}^{ – 2x}}}}\) A1
\({{\text{e}}^y} = \frac{1}{3}(1 + {{\text{e}}^{ – 2x}})\) M1
Now \({{\text{e}}^{ – 2x}} = 3{{\text{e}}^y} – 1\) A1
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{ – 2(3{{\text{e}}^y} – 1)}}{{1 + 3{{\text{e}}^y} – 1}}\) A1
\( = – \frac{2}{{3{{\text{e}}^y}}}(3{{\text{e}}^y} – 1)\)
\( = – \frac{2}{3}(3 – {{\text{e}}^{ – y}})\) A1
\( = \frac{2}{3}({{\text{e}}^{ – y}} – 3)\) AG
OR
\({{\text{e}}^y} = \frac{1}{3}(1 + {{\text{e}}^{ – 2x}})\) M1A1
\({{\text{e}}^y}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{2}{3}{{\text{e}}^{ – 2x}}\) M1A1
Now \({{\text{e}}^{ – 2x}} = 3{{\text{e}}^y} – 1\) (A1)
\( \Rightarrow {{\text{e}}^y}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{2}{3}(3{{\text{e}}^y} – 1)\)
\( \Rightarrow \frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{2}{3}{{\text{e}}^{ – y}}(3{{\text{e}}^y} – 1)\) (A1)
\( = \frac{2}{3}( – 3 + {{\text{e}}^{ – y}})\) (A1)
\( = \frac{2}{3}({{\text{e}}^{ – y}} – 3)\) AG
Note: Only two of the three (A1) marks may be implied.
[7 marks]
Examiners report
Solutions were generally disappointing with many candidates being awarded the first 2 or 3 marks, but then going no further.
Question
(a) Differentiate \(f(x) = \arcsin x + 2\sqrt {1 – {x^2}} \) , \(x \in [ – 1, 1]\) .
(b) Find the coordinates of the point on the graph of \(y = f (x)\) in \([ – 1, 1]\), where the gradient of the tangent to the curve is zero.
Answer/Explanation
Markscheme
(a) \(f'(x) = \frac{1}{{\sqrt {1 – {x^2}} }} – \frac{{2x}}{{\sqrt {1 – {x^2}} }}\) \(\left( { = \frac{{1 – 2x}}{{\sqrt {1 – {x^2}} }}} \right)\) M1A1A1
Note: Award A1 for first term,
M1A1 for second term (M1 for attempting chain rule).
(b) \(f'(x) = 0\) (M1)
\(x = 0.5\) , \(y = 2.26\) or \(\frac{\pi }{6} + \sqrt 3 \) (accept (\(0.500\), \(2.26\)) A1A1 N3
[6 marks]
Examiners report
Most candidates scored well on this question, showing competence at non-trivial differentiation. The follow through rules allowed candidates to recover from minor errors in part (a). Some candidates demonstrated their resourcefulness in using their GDC to answer part (b) even when they had been unable to gain full marks on part (a).
Question
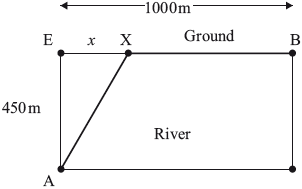
Engineers need to lay pipes to connect two cities A and B that are separated by a river of width 450 metres as shown in the following diagram. They plan to lay the pipes under the river from A to X and then under the ground from X to B. The cost of laying the pipes under the river is five times the cost of laying the pipes under the ground.
Let \({\text{EX}} = x\).
Let k be the cost, in dollars per metre, of laying the pipes under the ground.
(a) Show that the total cost C, in dollars, of laying the pipes from A to B is given by \(C = 5k\sqrt {202\,500 + {x^2}} + (1000 – x)k\).
(b) (i) Find \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\).
(ii) Hence find the value of x for which the total cost is a minimum, justifying that this value is a minimum.
(c) Find the minimum total cost in terms of k.
The angle at which the pipes are joined is \({\rm{A\hat XB}} = \theta \).
(d) Find \(\theta \) for the value of x calculated in (b).
For safety reasons \(\theta \) must be at least 120°.
Given this new requirement,
(e) (i) find the new value of x which minimises the total cost;
(ii) find the percentage increase in the minimum total cost.
Answer/Explanation
Markscheme
(a) \(C = {\text{AX}} \times 5k + {\text{XB}} \times k\) (M1)
Note: Award (M1) for attempting to express the cost in terms of AX, XB and k.
\( = 5k\sqrt {{{450}^2} + {x^2}} + (1000 – x)k\) A1
\( = 5k\sqrt {202\,500 + {x^2}} + (1000 – x)k\) AG
[2 marks]
(b) (i) \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = k\left[ {\frac{{5 \times 2x}}{{2\sqrt {202\,500 + {x^2}} }} – 1} \right] = k\left( {\frac{{5x}}{{\sqrt {202\,500 + {x^2}} }} – 1} \right)\) M1A1
Note: Award M1 for an attempt to differentiate and A1 for the correct derivative.
(ii) attempting to solve \(\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0\) M1
\(\frac{5}{{\sqrt {202\,500 + {x^2}} }} = 1\) (A1)
\(x = 91.9{\text{ (m) }}\left( { = \frac{{75\sqrt 6 }}{2}{\text{ (m)}}} \right)\) A1
METHOD 1
for example,
at \(x = 91\frac{{{\text{d}}C}}{{{\text{d}}x}} = – 0.00895k < 0\) M1
at \(x = 92\frac{{{\text{d}}C}}{{{\text{d}}x}} = 0.001506k > 0\) A1
Note: Award M1 for attempting to find the gradient either side of \(x = 91.9\) and A1 for two correct values.
thus \(x = 91.9\) gives a minimum AG
METHOD 2
\(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = \frac{{1\,012\,500k}}{{{{\left( {{x^2} + 202\,500} \right)}^{\frac{3}{2}}}}}\)
at \(x = 91.9\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}} = 0.010451k > 0\) (M1)A1
Note: Award M1 for attempting to find the second derivative and A1 for the correct value.
Note: If \(\frac{{{{\text{d}}^2}C}}{{{\text{d}}{x^2}}}\) is obtained and its value at \(x = 91.9\) is not calculated, award (M1)A1 for correct reasoning eg, both numerator and denominator are positive at \(x = 91.9\).
thus \(x = 91.9\) gives a minimum AG
METHOD 3
Sketching the graph of either C versus x or \(\frac{{{\text{d}}C}}{{{\text{d}}x}}\) versus x. M1
Clearly indicating that \(x = 91.9\) gives the minimum on their graph. A1
[7 marks]
(c) \({C_{\min }} = 3205k\) A1
Note: Accept 3200k.
Accept 3204k.
[1 mark]
(d) \(\arctan \left( {\frac{{450}}{{91.855865{\text{K}}}}} \right) = 78.463{\text{K}}^\circ \) M1
\(180 – 78.463{\text{K = 101.537K}}\)
\( = 102^\circ \) A1
[2 marks]
(e) (i) when \(\theta = 120^\circ ,{\text{ }}x = 260{\text{ (m) }}\left( {\frac{{450}}{{\sqrt 3 }}{\text{ (m)}}} \right)\) A1
(ii) \(\frac{{133.728{\text{K}}}}{{3204.5407685{\text{K}}}} \times 100\% \) M1
\( = 4.17{\text{ (% )}}\) A1
[3 marks]
Total [15 marks]
Examiners report
Question
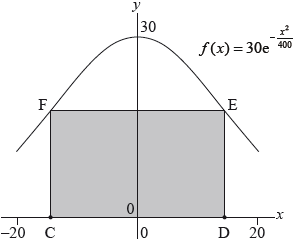
The following diagram shows a vertical cross section of a building. The cross section of the roof of the building can be modelled by the curve \(f(x) = 30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\), where \( – 20 \le x \le 20\).
Ground level is represented by the \(x\)-axis.
Find \(f”(x)\).
Show that the gradient of the roof function is greatest when \(x = – \sqrt {200} \).
The cross section of the living space under the roof can be modelled by a rectangle \(CDEF\) with points \({\text{C}}( – a,{\text{ }}0)\) and \({\text{D}}(a,{\text{ }}0)\), where \(0 < a \le 20\).
Show that the maximum area \(A\) of the rectangle \(CDEF\) is \(600\sqrt 2 {{\text{e}}^{ – \frac{1}{2}}}\).
A function \(I\) is known as the Insulation Factor of \(CDEF\). The function is defined as \(I(a) = \frac{{P(a)}}{{A(a)}}\) where \({\text{P}} = {\text{Perimeter}}\) and \({\text{A}} = {\text{Area of the rectangle}}\).
(i) Find an expression for \(P\) in terms of \(a\).
(ii) Find the value of \(a\) which minimizes \(I\).
(iii) Using the value of \(a\) found in part (ii) calculate the percentage of the cross sectional area under the whole roof that is not included in the cross section of the living space.
Answer/Explanation
Markscheme
\(f'(x) = 30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}} \bullet – \frac{{2x}}{{400}}\;\;\;\left( { = – \frac{{3x}}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}} \right)\) M1A1
Note: Award M1 for attempting to use the chain rule.
\(f”(x) = – \frac{3}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}} + \frac{{3{x^2}}}{{4000}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\;\;\;\left( { = \frac{3}{{20}}{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}\left( {\frac{{{x^2}}}{{200}} – 1} \right)} \right)\) M1A1
Note: Award M1 for attempting to use the product rule.
[4 marks]
the roof function has maximum gradient when \(f”(x) = 0\) (M1)
Note: Award (M1) for attempting to find \(f”\left( { – \sqrt {200} } \right)\).
EITHER
\( = 0\) A1
OR
\(f”(x) = 0 \Rightarrow x = \pm \sqrt {200} \) A1
THEN
valid argument for maximum such as reference to an appropriate graph or change in the sign of \(f”(x)\) eg \(f”( – 15) = 0.010 \ldots ( > 0)\) and \(f”( – 14) = – 0.001 \ldots ( < 0)\) R1
\( \Rightarrow x = – \sqrt {200} \) AG
[3 marks]
\(A = 2a \bullet 30{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}\;\;\;\left( { = 60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} = – 400g'(a)} \right)\) (M1)(A1)
EITHER
\(\frac{{{\text{d}}A}}{{{\text{d}}a}} = 60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} \bullet – \frac{a}{{200}} + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}} = 0 \Rightarrow a = \sqrt {200} {\text{ }}\left( { – 400f”(a) = 0 \Rightarrow a = \sqrt {200} } \right)\) M1A1
OR
by symmetry eg \(a = – \sqrt {200} \) found in (b) or \({A_{{\text{max}}}}\) coincides with \(f”(a) = 0\) R1
\( \Rightarrow a = \sqrt {200} \) A1
Note: Award A0(M1)(A1)M0M1 for candidates who start with \(a = \sqrt {200} \) and do not provide any justification for the maximum area. Condone use of \(x\).
THEN
\({A_{{\text{max}}}} = 60 \bullet \sqrt {200} {{\text{e}}^{ – \frac{{200}}{{400}}}}\) M1
\( = 600\sqrt 2 {{\text{e}}^{ – \frac{1}{2}}}\) AG
[5 marks]
(i) perimeter \( = 4a + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}\) A1A1
Note: Condone use of \(x\).
(ii) \(I(a) = \frac{{4a + 60{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}}}{{60a{{\text{e}}^{ – \frac{{{a^2}}}{{400}}}}}}\) (A1)
graphing \(I(a)\) or other valid method to find the minimum (M1)
\(a = 12.6\) A1
(iii) area under roof \( = \int_{ – 20}^{20} {30{{\text{e}}^{ – \frac{{{x^2}}}{{400}}}}} {\text{d}}x\) M1
\( = 896.18 \ldots \) (A1)
area of living space \( = 60 \cdot (12.6…) \cdot e – {\frac{{(12.6…)}}{{400}}^2} = 508.56…\)
percentage of empty space \( = 43.3\% \) A1
[9 marks]
Total [21 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the curve, \(C\) defined by the equation \({y^2} – 2xy = 5 – {{\text{e}}^x}\). The point A lies on \(C\) and has coordinates \((0,{\text{ }}a),{\text{ }}a > 0\).
Find the value of \(a\).
Show that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\).
Find the equation of the normal to \(C\) at the point A.
Find the coordinates of the second point at which the normal found in part (c) intersects \(C\).
Given that \(v = {y^3},{\text{ }}y > 0\), find \(\frac{{{\text{d}}v}}{{{\text{d}}x}}\) at \(x = 0\).
Answer/Explanation
Markscheme
\({a^2} = 5 – 1\) (M1)
\(a = 2\) A1
[2 marks]
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} – \left( {2x\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2y} \right) = – {{\text{e}}^x}\) M1A1A1A1
Note: Award M1 for an attempt at implicit differentiation, A1 for each part.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{2y – {{\text{e}}^x}}}{{2(y – x)}}\) AG
[4 marks]
at \(x = 0,{\text{ }}\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{3}{4}\) (A1)
finding the negative reciprocal of a number (M1)
gradient of normal is \( – \frac{4}{3}\)
\(y = – \frac{4}{3}x + 2\) A1
[3 marks]
substituting linear expression (M1)
\({\left( { – \frac{4}{3}x + 2} \right)^2} – 2x\left( { – \frac{4}{3}x + 2} \right) + {{\text{e}}^x} – 5 = 0\) or equivalent
\(x = 1.56\) (M1)A1
\(y = – 0.0779\) A1
\((1.56,{\text{ }} – 0.0779)\)
[4 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3{y^2}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = 3 \times 4 \times \frac{3}{4} = 9\) A1
[3 marks]
Examiners report
Parts (a) to (c) were generally well done.
Parts (a) to (c) were generally well done.
Parts (a) to (c) were generally well done although a significant number of students found the equation of the tangent rather than the normal in part (c).
Whilst many were able to make a start on part (d), fewer students had the necessary calculator skills to work it though correctly.
There were many overly complicated solutions to part (e), some of which were successful.
Question
The functions \(f\) and \(g\) are defined by
\[f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2},{\text{ }}x \in \mathbb{R}\]
\[g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2},{\text{ }}x \in \mathbb{R}\]
Let \(h(x) = nf(x) + g(x)\) where \(n \in \mathbb{R},{\text{ }}n > 1\).
Let \(t(x) = \frac{{g(x)}}{{f(x)}}\).
(i) Show that \(\frac{1}{{4f(x) – 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\).
(ii) Use the substitution \(u = {{\text{e}}^x}\) to find \(\int_0^{\ln 3} {\frac{1}{{4f(x) – 2g(x)}}} {\text{d}}x\). Give your answer in the form \(\frac{{\pi \sqrt a }}{b}\) where \(a,{\text{ }}b \in {\mathbb{Z}^ + }\).
(i) By forming a quadratic equation in \({{\text{e}}^x}\), solve the equation \(h(x) = k\), where \(k \in {\mathbb{R}^ + }\).
(ii) Hence or otherwise show that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{n^2} – 1} \) and \(k \in {\mathbb{R}^ + }\).
(i) Show that \(t'(x) = \frac{{{{[f(x)]}^2} – {{[g(x)]}^2}}}{{{{[f(x)]}^2}}}\) for \(x \in \mathbb{R}\).
(ii) Hence show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).
Answer/Explanation
Markscheme
(i) \(\frac{1}{{4\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right) – 2\left( {\frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}} \right)}}\) (M1)
\( = \frac{1}{{2({{\text{e}}^x} + {{\text{e}}^{ – x}}) – ({{\text{e}}^x} – {{\text{e}}^{ – x}})}}\) (A1)
\( = \frac{1}{{{{\text{e}}^x} + 3{{\text{e}}^{ – x}}}}\) A1
\( = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\) AG
(ii) \(u = {{\text{e}}^x} \Rightarrow {\text{d}}u = {{\text{e}}^x}{\text{d}}x\) A1
\(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) M1
(when \(x = 0,{\text{ }}u = 1\) and when \(x = \ln 3,{\text{ }}u = 3\))
\(\int_1^3 {\frac{1}{{{u^2} + 3}}{\text{d}}u\left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{u}{{\sqrt 3 }}} \right)} \right]_1^3} \) M1A1
\(\left( { = \left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{{{{\text{e}}^x}}}{{\sqrt 3 }}} \right)} \right]_0^{\ln 3}} \right)\)
\( = \frac{{\pi \sqrt 3 }}{9} – \frac{{\pi \sqrt 3 }}{{18}}\) (M1)
\( = \frac{{\pi \sqrt 3 }}{{18}}\) A1
[9 marks]
(i) \((n + 1){{\text{e}}^{2x}} – 2k{{\text{e}}^x} + (n – 1) = 0\) M1A1
\({{\text{e}}^x} = \frac{{2k \pm \sqrt {4{k^2} – 4({n^2} – 1)} }}{{2(n + 1)}}\) M1
\(x = \ln \left( {\frac{{k \pm \sqrt {{k^2} – {n^2} + 1} }}{{n + 1}}} \right)\) M1A1
(ii) for two real solutions, we require \(k > \sqrt {{k^2} – {n^2} + 1} \) R1
and we also require \({k^2} – {n^2} + 1 > 0\) R1
\({k^2} > {n^2} – 1\) A1
\( \Rightarrow k > \sqrt {{n^2} – 1} {\text{ }}({\text{ }}k \in {\mathbb{R}^ + })\) AG
[8 marks]
METHOD 1
\(t(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}\)
\(t'(x) = \frac{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2} – {{({{\text{e}}^x} – {{\text{e}}^{ – x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\) M1A1
\(t'(x) = \frac{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right)}^2} – {{\left( {\frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}} \right)}^2}}}{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}} \right)}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 2
\(t'(x) = \frac{{f(x)g'(x) = g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 3
\(t(x) = ({{\text{e}}^x} – {{\text{e}}^{ – x}}){({{\text{e}}^x} + {{\text{e}}^{ – x}})^{ – 1}}\)
\(t'(x) = 1 – \frac{{{{({{\text{e}}^x} – {{\text{e}}^{ – x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\) M1A1
\( = 1 – \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 4
\(t'(x) = \frac{{g'(x)}}{{f(x)}} – \frac{{g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) gives \(t'(x) = 1 – \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} – {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
(ii) METHOD 1
\({\left[ {f(x)} \right]^2} > {\left[ {g(x)} \right]^2}\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ – x}}\) and \({{\text{e}}^x} – {{\text{e}}^{ – x}}\).
METHOD 2
\({\left[ {f(x)} \right]^2} – {\left[ {g(x)} \right]^2} = 1\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ – x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} – {{\text{e}}^{ – x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ – x}}\) and \({{\text{e}}^x} – {{\text{e}}^{ – x}}\).
METHOD 3
\(t'(x) = \frac{4}{{{{({{\text{e}}^x} + {{\text{e}}^{ – x}})}^2}}}\)
\({\left( {{{\text{e}}^x} + {{\text{e}}^{ – x}}} \right)^2} > 0\) M1A1
\(\frac{4}{{{{\left( {{{\text{e}}^x} + {{\text{e}}^{ – x}}} \right)}^2}}} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
[6 marks]
Examiners report
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
Part (a)(i) was reasonably well done with most candidates able to show that \(\frac{1}{{4f(x) – 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\). In part (a)(ii), a number of candidates correctly used the required substitution to obtain \(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) but then thought that the antiderivative involved natural log rather than arctan.
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
In part (b)(i), a reasonable number of candidates were able to form a quadratic in \({{\text{e}}^x}\) (involving parameters \(n\) and \(k\)) and then make some progress towards solving for \({{\text{e}}^x}\) in terms of \(n\) and \(k\). Having got that far, a small number of candidates recognised to then take the natural logarithm of both sides and hence solve \(h(x) = k\) for \(\chi \). In part (b)(ii), a small number of candidates were able to show from their solutions to part (b)(i) or through the use of the discriminant that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{k^2} – {n^2} + 1} \) and \(k > \sqrt {{n^2} – 1} \).
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
It was pleasing to see the number of candidates who attempted part (c). In part (c)(i), a large number of candidates were able to correctly apply either the quotient rule or the product rule to find \(t'(x)\). A smaller number of candidates were then able to show equivalence between the form of \(t'(x)\) they had obtained and the form of \(t'(x)\) required in the question. A pleasing number of candidates were able to exploit the property that \(f'(x) = g(x)\) and \(g'(x) = f(x)\). As with part (c)(i), part (c)(ii) could be successfully tackled in a number of ways. The best candidates offered concise logical reasoning to show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).
Question
An earth satellite moves in a path that can be described by the curve \(72.5{x^2} + 71.5{y^2} = 1\) where \(x = x(t)\) and \(y = y(t)\) are in thousands of kilometres and \(t\) is time in seconds.
Given that \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 7.75 \times {10^{ – 5}}\) when \(x = 3.2 \times {10^{ – 3}}\), find the possible values of \(\frac{{{\text{d}}y}}{{{\text{d}}t}}\).
Give your answers in standard form.
Answer/Explanation
Markscheme
METHOD 1
substituting for \(x\) and attempting to solve for \(y\) (or vice versa) (M1)
\(y = ( \pm )0.11821 \ldots \) (A1)
EITHER
\(145x + 143y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0{\text{ }}\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{145x}}{{143y}}} \right)\) M1A1
OR
\(145x\frac{{{\text{d}}x}}{{{\text{d}}t}} + 143y\frac{{{\text{d}}y}}{{{\text{d}}t}} = 0\) M1A1
THEN
attempting to find \(\frac{{{\text{d}}x}}{{{\text{d}}t}}{\text{ }}\left( {\frac{{{\text{d}}y}}{{{\text{d}}t}} = – \frac{{145(3.2 \times {{10}^{ – 3}})}}{{143\left( {( \pm )0.11821 \ldots } \right)}} \times (7.75 \times {{10}^{ – 5}})} \right)\) (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}t}} = \pm 2.13 \times {10^{ – 6}}\) A1
Note: Award all marks except the final A1 to candidates who do not consider ±.
METHOD 2
\(y = ( \pm )\sqrt {\frac{{1 – 72.5{x^2}}}{{71.5}}} \) M1A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = ( \pm )0.0274 \ldots \) (M1)(A1)
\(\frac{{{\text{d}}y}}{{{\text{d}}t}} = ( \pm )0.0274 \ldots \times 7.75 \times {10^{ – 5}}\) (M1)
\(\frac{{{\text{d}}y}}{{{\text{d}}t}} = \pm 2.13 \times {10^{ – 6}}\) A1
Note: Award all marks except the final A1 to candidates who do not consider ±.
[6 marks]
Examiners report
Question
Let the function \(f\) be defined by \(f(x) = \frac{{2 – {{\text{e}}^x}}}{{2{{\text{e}}^x} – 1}},{\text{ }}x \in D\).
Determine \(D\), the largest possible domain of \(f\).
Show that the graph of \(f\) has three asymptotes and state their equations.
Show that \(f'(x) = – \frac{{3{{\text{e}}^x}}}{{{{(2{{\text{e}}^x} – 1)}^2}}}\).
Use your answers from parts (b) and (c) to justify that \(f\) has an inverse and state its domain.
Find an expression for \({f^{ – 1}}(x)\).
Consider the region \(R\) enclosed by the graph of \(y = f(x)\) and the axes.
Find the volume of the solid obtained when \(R\) is rotated through \(2\pi \) about the \(y\)-axis.
Answer/Explanation
Markscheme
attempting to solve either \(2{{\text{e}}^x} – 1 = 0\) or \(2{{\text{e}}^x} – 1 \ne 0\) for \(x\) (M1)
\(D = \mathbb{R}\backslash \left\{ { – \ln 2} \right\}\) (or equivalent eg \(x \ne – \ln 2\)) A1
Note: Accept \(D = \mathbb{R}\backslash \left\{ { – 0.693} \right\}\) or equivalent eg \(x \ne – 0.693\).
[2 marks]
considering \(\mathop {\lim }\limits_{x \to – \ln 2} f(x)\) (M1)
\(x = – \ln 2{\text{ }}(x = – 0.693)\) A1
considering one of \(\mathop {\lim }\limits_{x \to – \infty } f(x)\) or \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) M1
\(\mathop {\lim }\limits_{x \to – \infty } f(x) = – 2 \Rightarrow y = – 2\) A1
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = – \frac{1}{2} \Rightarrow y = – \frac{1}{2}\) A1
Note: Award A0A0 for \(y = – 2\) and \(y = – \frac{1}{2}\) stated without any justification.
[5 marks]
\(f'(x) = \frac{{ – {{\text{e}}^x}(2{{\text{e}}^x} – 1) – 2{{\text{e}}^x}(2 – {{\text{e}}^x})}}{{{{(2{{\text{e}}^x} – 1)}^2}}}\) M1A1A1
\( = – \frac{{3{{\text{e}}^x}}}{{{{(2{{\text{e}}^x} – 1)}^2}}}\) AG
[3 marks]
\(f'(x) < 0{\text{ (for all }}x \in D) \Rightarrow f\) is (strictly) decreasing R1
Note: Award R1 for a statement such as \(f'(x) \ne 0\) and so the graph of \(f\) has no turning points.
one branch is above the upper horizontal asymptote and the other branch is below the lower horizontal asymptote R1
\(f\) has an inverse AG
\( – \infty < x < – 2 \cup – \frac{1}{2} < x < \infty \) A2
Note: Award A2 if the domain of the inverse is seen in either part (d) or in part (e).
[4 marks]
\(x = \frac{{2 – {{\text{e}}^y}}}{{2{{\text{e}}^y} – 1}}\) M1
Note: Award M1 for interchanging \(x\) and \(y\) (can be done at a later stage).
\(2x{{\text{e}}^y} – x = 2 – {{\text{e}}^y}\) M1
\({{\text{e}}^y}(2x + 1) = x + 2\) A1
\({f^{ – 1}}(x) = \ln \left( {\frac{{x + 2}}{{2x + 1}}} \right){\text{ }}\left( {{f^{ – 1}}(x) = \ln (x + 2) – \ln (2x + 1)} \right)\) A1
[4 marks]
use of \(V = \pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
\( = \pi \int_0^1 {{{\left( {\ln \left( {\frac{{y + 2}}{{2y + 1}}} \right)} \right)}^2}{\text{d}}y} \) (A1)(A1)
Note: Award (A1) for the correct integrand and (A1) for the limits.
\( = 0.331\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
A water trough which is 10 metres long has a uniform cross-section in the shape of a semicircle with radius 0.5 metres. It is partly filled with water as shown in the following diagram of the cross-section. The centre of the circle is O and the angle KOL is \(\theta \) radians.
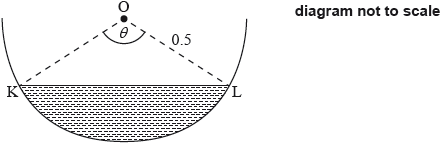
The volume of water is increasing at a constant rate of \(0.0008{\text{ }}{{\text{m}}^3}{{\text{s}}^{ – 1}}\).
Find an expression for the volume of water \(V{\text{ }}({{\text{m}}^3})\) in the trough in terms of \(\theta \).
Calculate \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) when \(\theta = \frac{\pi }{3}\).
Answer/Explanation
Markscheme
area of segment \( = \frac{1}{2} \times {0.5^2} \times (\theta – \sin \theta )\) M1A1
\(V = {\text{area of segment}} \times 10\)
\(V = \frac{5}{4}(\theta – \sin \theta )\) A1
[3 marks]
METHOD 1
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = \frac{5}{4}(1 – \cos \theta )\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) M1A1
\(0.0008 = \frac{5}{4}\left( {1 – \cos \frac{\pi }{3}} \right)\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128{\text{ }}({\text{rad}}\,{s^{ – 1}})\) A1
METHOD 2
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}V}}{{{\text{d}}\theta }} = \frac{5}{4}(1 – \cos \theta )\) A1
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{4 \times 0.0008}}{{5\left( {1 – \cos \frac{\pi }{3}} \right)}}\) (M1)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.00128\left( {\frac{4}{{3125}}} \right)({\text{rad }}{s^{ – 1}})\) A1
[4 marks]
Examiners report
[N/A]
[N/A]
Question
Consider \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right)\)
The function \(f\) is defined by \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in D\)
The function \(g\) is defined by \(g(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[\).
Find the largest possible domain \(D\) for \(f\) to be a function.
Sketch the graph of \(y = f(x)\) showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why \(f\) is an even function.
Explain why the inverse function \({f^{ – 1}}\) does not exist.
Find the inverse function \({g^{ – 1}}\) and state its domain.
Find \(g'(x)\).
Hence, show that there are no solutions to \(g'(x) = 0\);
Hence, show that there are no solutions to \(({g^{ – 1}})'(x) = 0\).
Answer/Explanation
Markscheme
\({x^2} – 1 > 0\) (M1)
\(x < – 1\) or \(x > 1\) A1
[2 marks]
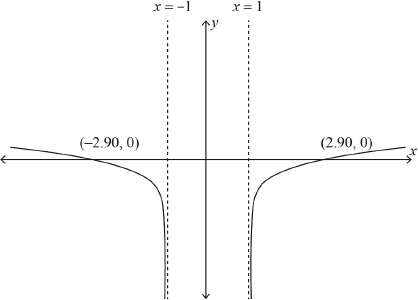
shape A1
\(x = 1\) and \(x = – 1\) A1
\(x\)-intercepts A1
[3 marks]
EITHER
\(f\) is symmetrical about the \(y\)-axis R1
OR
\(f( – x) = f(x)\) R1
[1 mark]
EITHER
\(f\) is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
\(x = – 1 + \ln \left( {\sqrt {{y^2} – 1} } \right)\) M1
\({{\text{e}}^{2x + 2}} = {y^2} – 1\) M1
\({g^{ – 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}\) A1A1
[4 marks]
\(g'(x) = \frac{1}{{\sqrt {{x^2} – 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} – 1} }}\) M1A1
\(g'(x) = \frac{x}{{{x^2} – 1}}\) A1
[3 marks]
\(g'(x) = \frac{x}{{{x^2} – 1}} = 0 \Rightarrow x = 0\) M1
which is not in the domain of \(g\) (hence no solutions to \(g'(x) = 0\)) R1
[2 marks]
\(({g^{ – 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}\) M1
as \({{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ – 1}})'(x) > 0\) so no solutions to \(({g^{ – 1}})'(x) = 0\) R1
Note: Accept: equation \({{\text{e}}^{2x + 2}} = 0\) has no solutions.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right)\)
The function \(f\) is defined by \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in D\)
The function \(g\) is defined by \(g(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[\).
Find the largest possible domain \(D\) for \(f\) to be a function.
Sketch the graph of \(y = f(x)\) showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why \(f\) is an even function.
Explain why the inverse function \({f^{ – 1}}\) does not exist.
Find the inverse function \({g^{ – 1}}\) and state its domain.
Find \(g'(x)\).
Hence, show that there are no solutions to \(g'(x) = 0\);
Hence, show that there are no solutions to \(({g^{ – 1}})'(x) = 0\).
Answer/Explanation
Markscheme
\({x^2} – 1 > 0\) (M1)
\(x < – 1\) or \(x > 1\) A1
[2 marks]

shape A1
\(x = 1\) and \(x = – 1\) A1
\(x\)-intercepts A1
[3 marks]
EITHER
\(f\) is symmetrical about the \(y\)-axis R1
OR
\(f( – x) = f(x)\) R1
[1 mark]
EITHER
\(f\) is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
\(x = – 1 + \ln \left( {\sqrt {{y^2} – 1} } \right)\) M1
\({{\text{e}}^{2x + 2}} = {y^2} – 1\) M1
\({g^{ – 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}\) A1A1
[4 marks]
\(g'(x) = \frac{1}{{\sqrt {{x^2} – 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} – 1} }}\) M1A1
\(g'(x) = \frac{x}{{{x^2} – 1}}\) A1
[3 marks]
\(g'(x) = \frac{x}{{{x^2} – 1}} = 0 \Rightarrow x = 0\) M1
which is not in the domain of \(g\) (hence no solutions to \(g'(x) = 0\)) R1
[2 marks]
\(({g^{ – 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}\) M1
as \({{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ – 1}})'(x) > 0\) so no solutions to \(({g^{ – 1}})'(x) = 0\) R1
Note: Accept: equation \({{\text{e}}^{2x + 2}} = 0\) has no solutions.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right)\)
The function \(f\) is defined by \(f(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in D\)
The function \(g\) is defined by \(g(x) = – 1 + \ln \left( {\sqrt {{x^2} – 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[\).
Find the largest possible domain \(D\) for \(f\) to be a function.
Sketch the graph of \(y = f(x)\) showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why \(f\) is an even function.
Explain why the inverse function \({f^{ – 1}}\) does not exist.
Find the inverse function \({g^{ – 1}}\) and state its domain.
Find \(g'(x)\).
Hence, show that there are no solutions to \(g'(x) = 0\);
Hence, show that there are no solutions to \(({g^{ – 1}})'(x) = 0\).
Answer/Explanation
Markscheme
\({x^2} – 1 > 0\) (M1)
\(x < – 1\) or \(x > 1\) A1
[2 marks]

shape A1
\(x = 1\) and \(x = – 1\) A1
\(x\)-intercepts A1
[3 marks]
EITHER
\(f\) is symmetrical about the \(y\)-axis R1
OR
\(f( – x) = f(x)\) R1
[1 mark]
EITHER
\(f\) is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
\(x = – 1 + \ln \left( {\sqrt {{y^2} – 1} } \right)\) M1
\({{\text{e}}^{2x + 2}} = {y^2} – 1\) M1
\({g^{ – 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}\) A1A1
[4 marks]
\(g'(x) = \frac{1}{{\sqrt {{x^2} – 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} – 1} }}\) M1A1
\(g'(x) = \frac{x}{{{x^2} – 1}}\) A1
[3 marks]
\(g'(x) = \frac{x}{{{x^2} – 1}} = 0 \Rightarrow x = 0\) M1
which is not in the domain of \(g\) (hence no solutions to \(g'(x) = 0\)) R1
[2 marks]
\(({g^{ – 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}\) M1
as \({{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ – 1}})'(x) > 0\) so no solutions to \(({g^{ – 1}})'(x) = 0\) R1
Note: Accept: equation \({{\text{e}}^{2x + 2}} = 0\) has no solutions.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]