Question
André wants to get from point A located in the sea to point Y located on a straight stretch of beach. P is the point on the beach nearest to A such that AP = 2 km and PY = 2 km. He does this by swimming in a straight line to a point Q located on the beach and then running to Y.
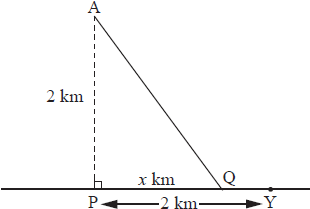
When André swims he covers 1 km in \(5\sqrt 5 \) minutes. When he runs he covers 1 km in 5 minutes.
(a) If PQ = x km, \(0 \leqslant x \leqslant 2\) , find an expression for the time T minutes taken by André to reach point Y.
(b) Show that \(\frac{{{\text{d}}T}}{{{\text{d}}x}} = \frac{{5\sqrt 5 x}}{{\sqrt {{x^2} + 4} }} – 5\).
(c) (i) Solve \(\frac{{{\text{d}}T}}{{{\text{d}}x}} = 0\).
(ii) Use the value of x found in part (c) (i) to determine the time, T minutes, taken for André to reach point Y.
(iii) Show that \(\frac{{{{\text{d}}^2}T}}{{{\text{d}}{x^2}}} = \frac{{20\sqrt 5 }}{{{{({x^2} + 4)}^{\frac{3}{2}}}}}\) and hence show that the time found in part (c) (ii) is a minimum.
▶️Answer/Explanation
Markscheme
(a) \({\text{AQ}} = \sqrt {{x^2} + 4} {\text{ (km)}}\) (A1)
\({\text{QY}} = (2 – x){\text{ (km)}}\) (A1)
\(T = 5\sqrt 5 {\text{AQ}} + 5{\text{QY}}\) (M1)
\({\text{ = 5}}\sqrt 5 \sqrt {({x^2} + 4)} + 5(2 – x){\text{ (mins)}}\) A1
[4 marks]
(b) Attempting to use the chain rule on \({\text{5}}\sqrt 5 \sqrt {({x^2} + 4)} \) (M1)
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {{\text{5}}\sqrt 5 \sqrt {({x^2} + 4)} } \right) = 5\sqrt 5 \times \frac{1}{2}{({x^2} + 4)^{ – \frac{1}{2}}} \times 2x\) A1
\(\left( { = \frac{{5\sqrt 5 x}}{{\sqrt {{x^2} + 4} }}} \right)\)
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {5(2 – x)} \right) = – 5\) A1
\(\frac{{{\text{d}}T}}{{{\text{d}}x}} = \frac{{5\sqrt 5 x}}{{\sqrt {{x^2} + 4} }} – 5\) AG N0
[3 marks]
(c) (i) \(\sqrt 5 x = \sqrt {{x^2} + 4} \) A1
Squaring both sides and rearranging to obtain \(5{x^2} = {x^2} + 4\) M1
x = 1 A1 N1
Note: Do not award the final A1 for stating a negative solution in final answer.
(ii) \(T = 5\sqrt 5 \sqrt {1 + 4} + 5(2 – 1)\) M1
= 30 (mins) A1 N1
Note: Allow FT on incorrect x value.
(iii) METHOD 1
Attempting to use the quotient rule M1
\(u = x{\text{ , }}v = \sqrt {{x^2} + 4} {\text{, }}\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1{\text{ and }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = x{({x^2} + 4)^{ – 1/2}}\) (A1)
\(\frac{{{{\text{d}}^2}T}}{{{\text{d}}{x^2}}} = 5\sqrt 5 \left[ {\frac{{\sqrt {{x^2} + 4} – \frac{1}{2}{{({x^2} + 4)}^{ – 1/2}} \times 2{x^2}}}{{({x^2} + 4)}}} \right]\) A1
Attempt to simplify (M1)
\( = \frac{{5\sqrt 5 }}{{{{({x^2} + 4)}^{3/2}}}}[{x^2} + 4 – {x^2}]\,\,\,\,\,\)or equivalent A1
\( = \frac{{20\sqrt 5 }}{{{{({x^2} + 4)}^{3/2}}}}\) AG
When \(x = 1{\text{ , }}\frac{{20\sqrt 5 }}{{{{({x^2} + 4)}^{3/2}}}} > 0\) and hence T = 30 is a minimum R1 N0
Note: Allow FT on incorrect x value, \(0 \leqslant x \leqslant 2\).
METHOD 2
Attempting to use the product rule M1
\(u = x{\text{ , }}v = \sqrt {{x^2} + 4} {\text{, }}\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1{\text{ and }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = x{({x^2} + 4)^{ – 1/2}}\) (A1)
\(\frac{{{{\text{d}}^2}T}}{{{\text{d}}{x^2}}} = 5\sqrt 5 {({x^2} + 4)^{ – 1/2}} – \frac{{5\sqrt 5 x}}{2}{({x^2} + 4)^{ – 3/2}} \times 2x\) A1
\(\left( { = \frac{{5\sqrt 5 }}{{{{({x^2} + 4)}^{1/2}}}} – \frac{{5\sqrt 5 {x^2}}}{{{{({x^2} + 4)}^{3/2}}}}} \right)\)
Attempt to simplify (M1)
\( = \frac{{5\sqrt 5 ({x^2} + 4) – 5\sqrt 5 {x^2}}}{{{{({x^2} + 4)}^{3/2}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( { = \frac{{5\sqrt 5 ({x^2} + 4 – {x^2})}}{{{{({x^2} + 4)}^{3/2}}}}} \right)\) A1
\( = \frac{{20\sqrt 5 }}{{{{({x^2} + 4)}^{3/2}}}}\) AG
When \(x = 1{\text{ , }}\frac{{20\sqrt 5 }}{{{{({x^2} + 4)}^{3/2}}}} > 0\) and hence T = 30 is a minimum R1 N0
Note: Allow FT on incorrect x value, \(0 \leqslant x \leqslant 2\).
[11 marks]
Total [18 marks]
Examiners report
Most candidates scored well on this question. The question tested their competence at algebraic manipulation and differentiation. A few candidates failed to extract from the context the correct relationship between velocity, distance and time.
Question
A packaging company makes boxes for chocolates. An example of a box is shown below. This box is closed and the top and bottom of the box are identical regular hexagons of side x cm.
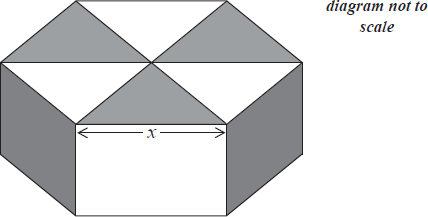
(a) Show that the area of each hexagon is \(\frac{{3\sqrt 3 {x^2}}}{2}{\text{c}}{{\text{m}}^2}\) .
(b) Given that the volume of the box is \({\text{90 c}}{{\text{m}}^2}\) , show that when \(x = \sqrt[3]{{20}}\) the total surface area of the box is a minimum, justifying that this value gives a minimum.
▶️Answer/Explanation
Markscheme
(a) Area of hexagon \( = 6 \times \frac{1}{2} \times x \times x \times \sin 60^\circ \) M1
\( = \frac{{3\sqrt 3 {x^2}}}{2}\) AG
(b) Let the height of the box be h
Volume \( = \frac{{3\sqrt 3 h{x^2}}}{2} = 90\) M1
Hence \(h = \frac{{60}}{{\sqrt 3 {x^2}}}\) A1
Surface area, \(A = 3\sqrt 3 {x^2} + 6hx\) M1
\( = 3\sqrt 3 {x^2} + \frac{{360}}{{\sqrt 3 }}{x^{ – 1}}\) A1
\(\frac{{{\text{d}}A}}{{{\text{d}}x}} = 6\sqrt 3 x – \frac{{360}}{{\sqrt 3 }}{x^{ – 2}}\) A1
\(\left( {\frac{{{\text{d}}A}}{{{\text{d}}x}} = 0} \right)\)
\(6\sqrt 3 {x^3} = \frac{{360}}{{\sqrt 3 }}\) M1
\({x^3} = 20\)
\(x = \sqrt[3]{{20}}\) AG
\(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{x^2}}} = 6\sqrt 3 + \frac{{720{x^{ – 3}}}}{{\sqrt 3 }}\)
which is positive when \(x = \sqrt[3]{{20}}\), and hence gives a minimum value. R1
[8 marks]
Examiners report
There were a number of wholly correct answers seen and the best candidates tackled the question well. However, many candidates did not seem to understand what was expected in such a problem. It was disappointing that a significant number of candidates were unable to find the area of the hexagon.
Question
The diagram below shows a circular lake with centre O, diameter AB and radius 2 km.
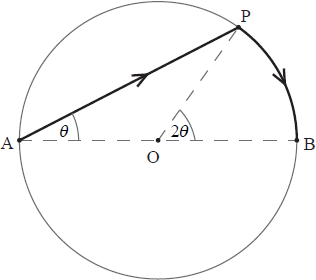
Jorg needs to get from A to B as quickly as possible. He considers rowing to point P and then walking to point B. He can row at \(3{\text{ km}}\,{{\text{h}}^{ – 1}}\) and walk at \(6{\text{ km}}\,{{\text{h}}^{ – 1}}\). Let \({\rm{P\hat AB}} = \theta \) radians, and t be the time in hours taken by Jorg to travel from A to B.
Show that \(t = \frac{2}{3}(2\cos \theta + \theta )\).
Find the value of \(\theta \) for which \(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = 0\).
What route should Jorg take to travel from A to B in the least amount of time?
Give reasons for your answer.
▶️Answer/Explanation
Markscheme
angle APB is a right angle
\( \Rightarrow \cos \theta = \frac{{{\text{AP}}}}{4} \Rightarrow {\text{AP}} = 4\cos \theta \) A1
Note: Allow correct use of cosine rule.
\({\text{arc PB}} = 2 \times 2\theta = 4\theta \) A1
\(t = \frac{{{\text{AP}}}}{3} + \frac{{{\text{PB}}}}{6}\) M1
Note: Allow use of their AP and their PB for the M1.
\( \Rightarrow t = \frac{{4\cos \theta }}{3} + \frac{{4\theta }}{6} = \frac{{4\cos \theta }}{3} + \frac{{2\theta }}{3} = \frac{2}{3}(2\cos \theta + \theta )\) AG
[3 marks]
\(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = \frac{2}{3}( – 2\sin \theta + 1)\) A1
\(\frac{2}{3}( – 2\sin \theta + 1) = 0 \Rightarrow \sin \theta = \frac{1}{2} \Rightarrow \theta = \frac{\pi }{6}\) (or 30 degrees) A1
[2 marks]
\(\frac{{{{\text{d}}^2}t}}{{{\text{d}}{\theta ^2}}} = – \frac{4}{3}\cos \theta < 0\,\,\,\,\left( {{\text{at }}\theta = \frac{\pi }{6}} \right)\) M1
\( \Rightarrow t\) is maximized at \(\theta = \frac{\pi }{6}\) R1
time needed to walk along arc AB is \(\frac{{2\pi }}{6}{\text{ (}} \approx {\text{1 hour)}}\)
time needed to row from A to B is \(\frac{4}{3}{\text{ (}} \approx {\text{1.33 hour)}}\)
hence, time is minimized in walking from A to B R1
[3 marks]
Examiners report
The fairly easy trigonometry challenged a large number of candidates.
Part (b) was very well done.
Satisfactory answers were very rarely seen for (c). Very few candidates realised that a minimum can occur at the beginning or end of an interval.
Question
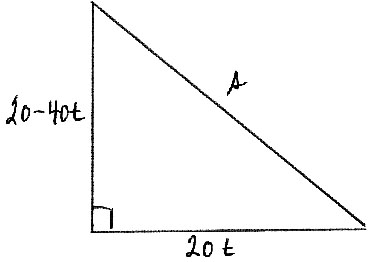
At 12:00 a boat is 20 km due south of a freighter. The boat is travelling due east at \(20{\text{ km}}\,{{\text{h}}^{ – 1}}\), and the freighter is travelling due south at \(40{\text{ km}}\,{{\text{h}}^{ – 1}}\).
Determine the time at which the two ships are closest to one another, and justify your answer.
If the visibility at sea is 9 km, determine whether or not the captains of the two ships can ever see each other’s ship.
▶️Answer/Explanation
Markscheme
 (M1)
(M1)
\({s^2} = {(20t)^2} + {(20 – 40t)^2}\) M1
\({s^2} = 2000{t^2} – 1600t + 400\) A1
to minimize s it is enough to minimize \({s^2}\)
\(f'(t) = 4000t – 1600\) A1
setting \(f'(t)\) equal to 0 M1
\(4000t – 1600 = 0 \Rightarrow t = \frac{2}{5}\) or 24 minutes A1
\(f”(t) = 4000 > 0\) M1
\( \Rightarrow \) at \(t = \frac{2}{5},{\text{ }}f(t)\) is minimized
hence, the ships are closest at 12:24 A1
Note: accept solution based on s.
[8 marks]
\(f\left( {\frac{2}{5}} \right) = \sqrt {80} \) M1A1
since \(\sqrt {80} < 9\), the captains can see one another R1
[3 marks]
Examiners report
This was, disappointingly, a poorly answered question. Some tried to talk their way through the question without introducing the time variable. Even those who did use the distance as a function of time often did not check for a minimum.
This was, disappointingly, a poorly answered question. Some tried to talk their way through the question without introducing the time variable. Even those who did use the distance as a function of time often did not check for a minimum.
Question
At 12:00 a boat is 20 km due south of a freighter. The boat is travelling due east at \(20{\text{ km}}\,{{\text{h}}^{ – 1}}\), and the freighter is travelling due south at \(40{\text{ km}}\,{{\text{h}}^{ – 1}}\).
Determine the time at which the two ships are closest to one another, and justify your answer.
If the visibility at sea is 9 km, determine whether or not the captains of the two ships can ever see each other’s ship.
▶️Answer/Explanation
Markscheme
 (M1)
(M1)
\({s^2} = {(20t)^2} + {(20 – 40t)^2}\) M1
\({s^2} = 2000{t^2} – 1600t + 400\) A1
to minimize s it is enough to minimize \({s^2}\)
\(f'(t) = 4000t – 1600\) A1
setting \(f'(t)\) equal to 0 M1
\(4000t – 1600 = 0 \Rightarrow t = \frac{2}{5}\) or 24 minutes A1
\(f”(t) = 4000 > 0\) M1
\( \Rightarrow \) at \(t = \frac{2}{5},{\text{ }}f(t)\) is minimized
hence, the ships are closest at 12:24 A1
Note: accept solution based on s.
[8 marks]
\(f\left( {\frac{2}{5}} \right) = \sqrt {80} \) M1A1
since \(\sqrt {80} < 9\), the captains can see one another R1
[3 marks]
Examiners report
This was, disappointingly, a poorly answered question. Some tried to talk their way through the question without introducing the time variable. Even those who did use the distance as a function of time often did not check for a minimum.
This was, disappointingly, a poorly answered question. Some tried to talk their way through the question without introducing the time variable. Even those who did use the distance as a function of time often did not check for a minimum.
Question
Consider the function \(f(x) = \frac{{\ln x}}{x},{\text{ }}x > 0\).
The sketch below shows the graph of \(y = {\text{ }}f(x)\) and its tangent at a point A.
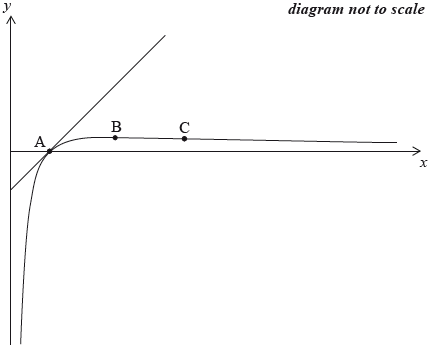
Show that \(f'(x) = \frac{{1 – \ln x}}{{{x^2}}}\).
Find the coordinates of B, at which the curve reaches its maximum value.
Find the coordinates of C, the point of inflexion on the curve.
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the equation of the tangent to the graph of \(f\) at the point A.
The graph of \(y = {\text{ }}f(x)\) crosses the \(x\)-axis at the point A.
Find the area enclosed by the curve \(y = f(x)\), the tangent at A, and the line \(x = {\text{e}}\).
▶️Answer/Explanation
Markscheme
\(f'(x) = \frac{{x \times \frac{1}{x} – \ln x}}{{{x^2}}}\) M1A1
\( = \frac{{1 – \ln x}}{{{x^2}}}\) AG
[2 marks]
\(\frac{{1 – \ln x}}{{{x^2}}} = 0\) has solution \(x = {\text{e}}\) M1A1
\(y = \frac{1}{{\text{e}}}\) A1
hence maximum at the point \(\left( {{\text{e, }}\frac{1}{{\text{e}}}} \right)\)
[3 marks]
\(f”(x) = \frac{{{x^2}\left( { – \frac{1}{x}} \right) – 2x(1 – \ln x)}}{{{x^4}}}\) M1A1
\( = \frac{{2\ln x – 3}}{{{x^3}}}\)
Note: The M1A1 should be awarded if the correct working appears in part (b).
point of inflexion where \(f”(x) = 0\) M1
so \(x = {{\text{e}}^{\frac{3}{2}}},{\text{ }}y = \frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}\) A1A1
C has coordinates \(\left( {{{\text{e}}^{\frac{3}{2}}},{\text{ }}\frac{3}{2}{{\text{e}}^{\frac{{ – 3}}{2}}}} \right)\)
[5 marks]
\(f(1) = 0\) A1
\(f'(1) = 1\) (A1)
\(y = x + c\) (M1)
through (1, 0)
equation is \(y = x – 1\) A1
[4 marks]
METHOD 1
area \( = \int_1^{\text{e}} {x – 1 – \frac{{\ln x}}{x}{\text{d}}x} \) M1A1A1
Note: Award M1 for integration of difference between line and curve, A1 for correct limits, A1 for correct expressions in either order.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}} ( + c)\) (M1)A1
\(\int {(x – 1){\text{d}}x = \frac{{{x^2}}}{2} – x( + c)} \) A1
\( = \left[ {\frac{1}{2}{x^2} – x – \frac{1}{2}{{(\ln x)}^2}} \right]_1^{\text{e}}\)
\( = \left( {\frac{1}{2}{{\text{e}}^2} – {\text{e}} – \frac{1}{2}} \right) – \left( {\frac{1}{2} – 1} \right)\)
\( = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
METHOD 2
area = area of triangle \( – \int_1^e {\frac{{\ln x}}{x}{\text{d}}x} \) M1A1
Note: A1 is for correct integral with limits and is dependent on the M1.
\(\int {\frac{{\ln x}}{x}{\text{d}}x = \frac{{{{(\ln x)}^2}}}{2}( + c)} \) (M1)A1
area of triangle \( = \frac{1}{2}(e – 1)(e – 1)\) M1A1
\(\frac{1}{2}(e – 1)(e – 1) – \left( {\frac{1}{2}} \right) = \frac{1}{2}{{\text{e}}^2} – {\text{e}}\) A1
[7 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The graph of the function \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\) is shown below.
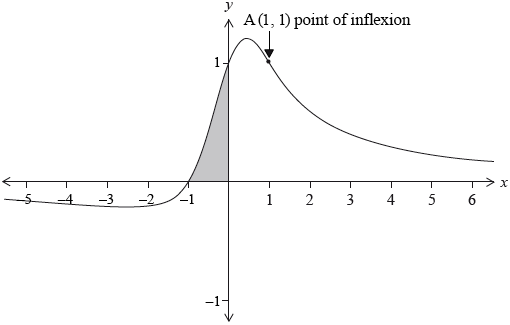
The point (1, 1) is a point of inflexion. There are two other points of inflexion.
Find \(f'(x)\).
Hence find the \(x\)-coordinates of the points where the gradient of the graph of \(f\) is zero.
Find \(f”(x)\) expressing your answer in the form \(\frac{{p(x)}}{{{{({x^2} + 1)}^3}}}\), where \(p(x)\) is a polynomial of degree 3.
Find the \(x\)-coordinates of the other two points of inflexion.
Find the area of the shaded region. Express your answer in the form \(\frac{\pi }{a} – \ln \sqrt b \), where \(a\) and \(b\) are integers.
Answer/Explanation
Markscheme
(a) \(f'(x) = \frac{{\left( {{x^2} + 1} \right) – 2x(x + 1)}}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{ }}\left( { = \frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} \right)\) M1A1
[2 marks]
\(\frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0\)
\(x = – 1 \pm \sqrt 2 \) A1
[1 mark]
\(f”(x) = \frac{{( – 2x – 2){{\left( {{x^2} + 1} \right)}^2} – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^4}}}\) A1A1
Note: Award A1 for \(( – 2x – 2){\left( {{x^2} + 1} \right)^2}\) or equivalent.
Note: Award A1 for \( – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)\) or equivalent.
\( = \frac{{( – 2x – 2)\left( {{x^2} + 1} \right) – 4x\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}\)
\( = \frac{{2{x^3} + 6{x^2} – 6x – 2}}{{{{\left( {{x^2} + 1} \right)}^3}}}\) A1
\(\left( { = \frac{{2\left( {{x^3} + 3{x^2} – 3x – 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}} \right)\)
[3 marks]
recognition that \((x – 1)\) is a factor (R1)
\((x – 1)\left( {{x^2} + bx + c} \right) = \left( {{x^3} + 3{x^2} – 3x – 1} \right)\) M1
\( \Rightarrow {x^2} + 4x + 1 = 0\) A1
\(x = – 2 \pm \sqrt 3 \) A1
Note: Allow long division / synthetic division.
[4 marks]
\(\int_{ – 1}^0 {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x} \) M1
\(\int {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x = \int {\frac{x}{{{x^2} + 1}}{\text{d}}x + \int {\frac{1}{{{x^2} + 1}}{\text{d}}x} } } \) M1
\( = \frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)\) A1A1
\( = \left[ {\frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)} \right]_{ – 1}^0 = \frac{1}{2}\ln 1 + \arctan 0 – \frac{1}{2}\ln 2 – \arctan ( – 1)\) M1
\( = \frac{\pi }{4} – \ln \sqrt 2 \) A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The graph of the function \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\) is shown below.

The point (1, 1) is a point of inflexion. There are two other points of inflexion.
Find \(f'(x)\).
Hence find the \(x\)-coordinates of the points where the gradient of the graph of \(f\) is zero.
Find \(f”(x)\) expressing your answer in the form \(\frac{{p(x)}}{{{{({x^2} + 1)}^3}}}\), where \(p(x)\) is a polynomial of degree 3.
Find the \(x\)-coordinates of the other two points of inflexion.
Find the area of the shaded region. Express your answer in the form \(\frac{\pi }{a} – \ln \sqrt b \), where \(a\) and \(b\) are integers.
Answer/Explanation
Markscheme
(a) \(f'(x) = \frac{{\left( {{x^2} + 1} \right) – 2x(x + 1)}}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{ }}\left( { = \frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}} \right)\) M1A1
[2 marks]
\(\frac{{ – {x^2} – 2x + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} = 0\)
\(x = – 1 \pm \sqrt 2 \) A1
[1 mark]
\(f”(x) = \frac{{( – 2x – 2){{\left( {{x^2} + 1} \right)}^2} – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^4}}}\) A1A1
Note: Award A1 for \(( – 2x – 2){\left( {{x^2} + 1} \right)^2}\) or equivalent.
Note: Award A1 for \( – 2(2x)\left( {{x^2} + 1} \right)\left( { – {x^2} – 2x + 1} \right)\) or equivalent.
\( = \frac{{( – 2x – 2)\left( {{x^2} + 1} \right) – 4x\left( { – {x^2} – 2x + 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}\)
\( = \frac{{2{x^3} + 6{x^2} – 6x – 2}}{{{{\left( {{x^2} + 1} \right)}^3}}}\) A1
\(\left( { = \frac{{2\left( {{x^3} + 3{x^2} – 3x – 1} \right)}}{{{{\left( {{x^2} + 1} \right)}^3}}}} \right)\)
[3 marks]
recognition that \((x – 1)\) is a factor (R1)
\((x – 1)\left( {{x^2} + bx + c} \right) = \left( {{x^3} + 3{x^2} – 3x – 1} \right)\) M1
\( \Rightarrow {x^2} + 4x + 1 = 0\) A1
\(x = – 2 \pm \sqrt 3 \) A1
Note: Allow long division / synthetic division.
[4 marks]
\(\int_{ – 1}^0 {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x} \) M1
\(\int {\frac{{x + 1}}{{{x^2} + 1}}{\text{d}}x = \int {\frac{x}{{{x^2} + 1}}{\text{d}}x + \int {\frac{1}{{{x^2} + 1}}{\text{d}}x} } } \) M1
\( = \frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)\) A1A1
\( = \left[ {\frac{1}{2}\ln \left( {{x^2} + 1} \right) + \arctan (x)} \right]_{ – 1}^0 = \frac{1}{2}\ln 1 + \arctan 0 – \frac{1}{2}\ln 2 – \arctan ( – 1)\) M1
\( = \frac{\pi }{4} – \ln \sqrt 2 \) A1
[6 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
A window is made in the shape of a rectangle with a semicircle of radius \(r\) metres on top, as shown in the diagram. The perimeter of the window is a constant P metres.

Find the area of the window in terms of P and \(r\).
Find the width of the window in terms of P when the area is a maximum, justifying that this is a maximum.
Show that in this case the height of the rectangle is equal to the radius of the semicircle.
Answer/Explanation
Markscheme
the width of the rectangle is \(2r\) and let the height of the rectangle be \(h\)
\(P = 2r + 2h + \pi r\) (A1)
\(A = 2rh + \frac{{\pi {r^2}}}{2}\) (A1)
\(h = \frac{{{\text{P}} – 2r – \pi r}}{2}\)
\(A = 2r\left( {\frac{{{\text{P}} – 2r – \pi r}}{2}} \right) + \frac{{\pi {r^2}}}{2}\,\,\,\left( { = \operatorname{P} r – 2{r^2} – \frac{{\pi {r^2}}}{2}} \right)\) M1A1
[4 marks]
\(\frac{{{\text{d}}A}}{{{\text{d}}r}} = {\text{P}} – 4r – \pi r\) A1
\(\frac{{{\text{d}}A}}{{{\text{d}}r}} = 0\) M1
\( \Rightarrow r = \frac{{\text{P}}}{{4 + \pi }}\) (A1)
hence the width is \(\frac{{2{\text{P}}}}{{4 + \pi }}\) A1
\(\frac{{{{\text{d}}^2}A}}{{{\text{d}}{r^2}}} = – 4 – \pi < 0\) R1
hence maximum AG
[5 marks]
EITHER
\(h = \frac{{{\text{P}} – 2r – \pi r}}{2}\)
\(h = \frac{{{\text{P}} – \frac{{2{\text{P}}}}{{4 + \pi }} – \frac{{{\text{P}}\pi }}{{4 + \pi }}}}{2}\) M1
\(h = \frac{{4{\text{P}} + \pi {\text{P}} – 2{\text{P}} – \pi {\text{P}}}}{{2(4 + \pi )}}\) A1
\(h = \frac{{\text{P}}}{{(4 + \pi )}} = r\) AG
OR
\(h = \frac{{{\text{P}} – 2r – \pi r}}{2}\)
\(P = r(4 + \pi )\) M1
\(h = \frac{{r(4 + \pi ) – 2r – \pi r}}{2}\) A1
\(h = \frac{{4r + \pi r – 2r – \pi r}}{2} = r\) AG
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider all closed cylinders of constant volume V.
(a) Find the cylinder of minimum total surface area (i.e. its dimensions in terms of V); justify your answer.
(b) Do there exist cylinders of maximum total surface area?
Answer/Explanation
Ans
(only guidelines and the final answers)
Let us call r the radius of the rectangle. The height will be \(h=\frac{V}{\pi r^{2}}\)
Then the total surface area is given by \(S=\frac{2V}{r}+2\pi r^{2}\)
(a) It is the cylinder with radius \(r=\sqrt[3]{\frac{V}{2\pi }}\) (and height \(h=\frac{V}{\pi r^{2}}\))
(b) The domain is \(r> 0\). There is no cylinder of maximum total surface area.
Question
Consider all closed cylinders of constant total surface area S.
(a) Find the cylinder of maximum volume (i.e. its dimensions in terms of S); justify your answer.
(b) Do there exist cylinders of minimum volume?
Answer/Explanation
Ans
(only guidelines and the final answers)
Let us call r the radius of the rectangle. The height will be \(h=\frac{S-2\, \pi\, r^{2}}{2\, \pi\, r}\)
(a) It is the cylinder with radius \(r=\sqrt{\frac{S}{6\pi }}\) (and height \(h=\frac{S-2\, \pi \, r^{2}}{2\, \pi \, r}\))
(b) The domain is \(0< r\leq \sqrt{\frac{S}{2\pi }}\). At the endpoint \(r=\sqrt{\frac{S}{2\pi }}\), the volume is \(0\).
Question
Consider the graph G of the function \(y=\sqrt{x}\) and its reflection G’ about the vertical line \(x=4\).
(a) Sketch the graphs of G and G’; indicate the coordinates of the intersection point of the two graphs.
A rectangle is drawn so that its lower vertices are on the x-axis and its upper vertices on the curves G and G’ respectively. The area of this rectangle is denoted by S.
(b) Find the maximum value of S. Justify your answer.
Answer/Explanation
Ans
\(S=(8-2x)\sqrt{x},\, S_{max}=\frac{32\sqrt{3}}{9}\)
Question
A point P\((x,x^{2})\) lies on the curve \(y=x^{2}\). Calculate the minimum distance from the point \(A\left ( 2,-\frac{1}{2} \right )\) to the point P . (Total 6 marks)
Answer/Explanation
Ans
METHOD 1
Let \(S=\textup{AP}^{2}=(x-2)^{2}+(x^{2}+\frac{1}{2})^{2}\) (M1)
The graph of S is as follows: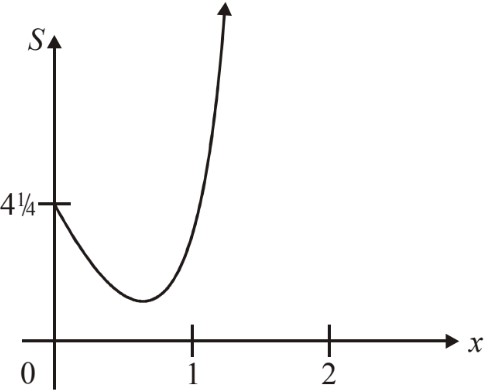
The minimum value of S is \(2.6686\). (G3)
Therefore the minimum distance \(=\sqrt{2.6686}=1.63\, (3\, \textup{s.f.})\) (A2)
OR
The minimum point is \((0.682,1.63)\) (G3)
The minimum distance is \(1.63\, (3\, \textup{s.f.})\) (G2) (C6)
METHOD 2
Let \(S=\textup{AP}^{2}=(x-2)^{2}+(x^{2}+\frac{1}{2})^{2}\). (M1)
\(\frac{\textup{d}S}{\textup{d}x}=2(x-2)+4x(x^{2}+\frac{1}{2})=4(x^{3}+x^{2}+1)\) (A2)
Solving \(x^{3}+x-1=0\) gives \(x=0.68233\) (G2)
Therefore, minimum distance \(=\sqrt{(0.68233-2)^{2}+(0.68233^{2}+0.5)^{2}}=1.63\) (A1) (C6) [6]
Question
The point \(B(a,b)\) b) is on the curve \(f(x)=x^{2}\) such that B is the point which is closest to A(6, 0). Calculate the value of a. (Total 6 marks)
Answer/Explanation
Ans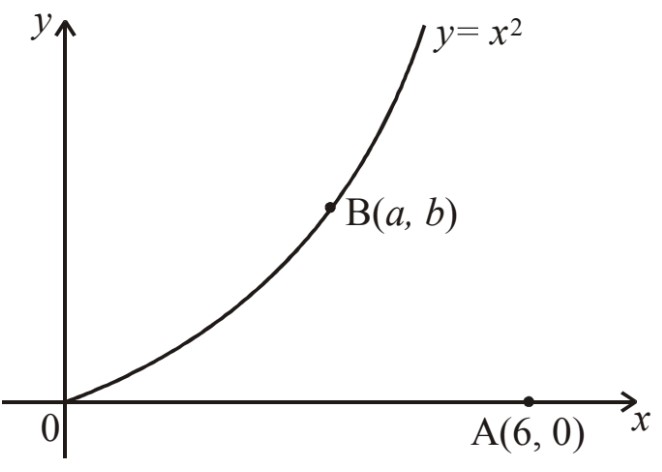
\(b=a^{2}\)
\(AB^{2}=(a-6)^{2}+a^{4}\) (M1)(A1)
Minimum value of \((x-6)^{2}+x^{4}\) occurs at \(x=1.33\) (G3)
\(=> a=1.33\) (G1) (C6) [6]
Question
A rectangle is drawn so that its lower vertices are on the x-axis and its upper vertices are on the curve \(y=\textup{sin}\, x\) where \(0\leq x\leq \pi \).
(a) Write down an expression for the area of the rectangle.
(b) Find the maximum area of the rectangle. (Total 3 marks)
Answer/Explanation
Ans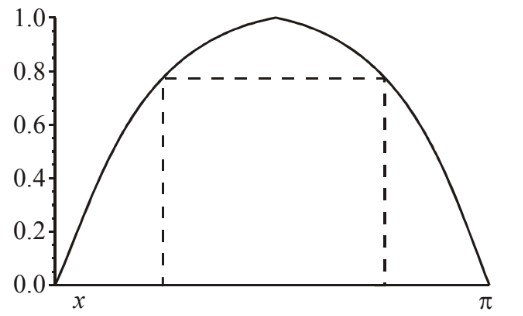
(a) Area \(=(\pi -2x)\, \textup{sin}\, x\). (M1)(A1) (C2)
(b) Maximum Area \(=1.12\) units2 (A1) (C1) [3]
Question
A rectangle is drawn so that its lower vertices are on the x-axis and its upper vertices are on the curve \(y=e^{-x^{2}}\). The area of this rectangle is denoted by A.
(a) Write down an expression for A in terms of x.
(b) Find the maximum value of A. (Total 6 marks)
Answer/Explanation
Ans
(a) \(A=2x \times e^{-x^{2}}=2xe^{-x^{2}}\) (M1)(A1) (C2)
(b) \(\frac{\textup{d}A}{\textup{d}x}=2(1-2x^{2})e^{-x^{2}}\) (A2)
\(\frac{\textup{d}A}{\textup{d}x}=0\, \textup{when}\, x=\frac{1}{\sqrt{2}}\) (A1)
\(A_{max}=\sqrt{2}e^{-\frac{1}{2}}\: \: (\textup{or}\, 0.858)\) (A1) (C4) [6]