Question
The curve \(y = {{\text{e}}^{ – x}} – x + 1\) intersects the x-axis at P.
(a) Find the x-coordinate of P.
(b) Find the area of the region completely enclosed by the curve and the coordinate axes.
▶️Answer/Explanation
Markscheme
(a) Either solving \({{\text{e}}^{ – x}} – x + 1 = 0\) for x, stating \({{\text{e}}^{ – x}} – x + 1 = 0\), stating P(x, 0) or using an appropriate sketch graph. M1
x = 1.28 A1 N1
Note: Accept P(1.28, 0) .
(b) Area \( = \int_0^{1.278…} {({{\text{e}}^{ – x}} – x + 1){\text{d}}x} \) M1A1
= 1.18 A1 N1
Note: Award M1A0A1 if the dx is absent.
[5 marks]
Examiners report
This was generally well done. In part (a), most candidates were able to find x = 1.28 successfully. A significant number of candidates were awarded an accuracy penalty for expressing answers to an incorrect number of significant figures.
Part (b) was generally well done. A number of candidates unfortunately omitted the dx in the integral while some candidates omitted to write down the definite integral and instead offered detailed instructions on how they obtained the answer using their GDC.
Question
The diagram below shows the graphs of \(y = \left| {\frac{3}{2}x – 3} \right|,{\text{ }}y = 3\) and a quadratic function, that all intersect in the same two points.

Given that the minimum value of the quadratic function is −3, find an expression for the area of the shaded region in the form \(\int_0^t {(a{x^2} + bx + c){\text{d}}x} \), where the constants a, b, c and t are to be determined. (Note: The integral does not need to be evaluated.)
▶️Answer/Explanation
Markscheme
\(\left| {\frac{3}{2}x – 3} \right| = 0\) when x = 2 (A1)
the equation of the parabola is \(y = p{(x – 2)^2} – 3\) (M1)
through \((0,{\text{ }}3) \Rightarrow 3 = 4p – 3 \Rightarrow p = \frac{3}{2}\) (M1)
the equation of the parabola is \(y = \frac{3}{2}{(x – 2)^2} – 3{\text{ }}\left( { = \frac{3}{2}{x^2} – 6x + 3} \right)\) A1
area \( = 2\int_0^2 {\left( {3 – \frac{3}{2}x} \right) – \left( {\frac{3}{2}{x^2} – 6x + 3} \right){\text{d}}x} \) M1M1A1
Note: Award M1 for recognizing symmetry to obtain \(2\int_0^2 , \)
M1 for the difference,
A1 for getting all parts correct.
\( = \int_0^2 {( – 3{x^2} + 9x){\text{d}}x} \) A1
[8 marks]
Examiners report
This was a difficult question and, although many students obtained partial marks, there were few completely correct solutions.
Question
The function f is defined by
\[f(x) = {({x^3} + 6{x^2} + 3x – 10)^{\frac{1}{2}}},{\text{ for }}x \in D,\]
where \(D \subseteq \mathbb{R}\) is the greatest possible domain of f.
(a) Find the roots of \(f(x) = 0\).
(b) Hence specify the set D.
(c) Find the coordinates of the local maximum on the graph \(y = f(x)\).
(d) Solve the equation \(f(x) = 3\).
(e) Sketch the graph of \(\left| y \right| = f(x),{\text{ for }}x \in D\).
(f) Find the area of the region completely enclosed by the graph of \(\left| y \right| = f(x)\)
▶️Answer/Explanation
Markscheme
(a) solving to obtain one root: 1, – 2 or – 5 A1
obtain other roots A1
[2 marks]
(b) \(D = x \in [ – 5,{\text{ }} – 2] \cup [1,{\text{ }}\infty {\text{)}}\) (or equivalent) M1A1
Note: M1 is for 1 finite and 1 infinite interval.
[2 marks]
(c) coordinates of local maximum \( – 3.73 – 2 – \sqrt 3 ,{\text{ }}3.22\sqrt {6\sqrt 3 } \) A1A1
[2 marks]
(d) use GDC to obtain one root: 1.41, – 3.18 or – 4.23 A1
obtain other roots A1
[2 marks]
(e)
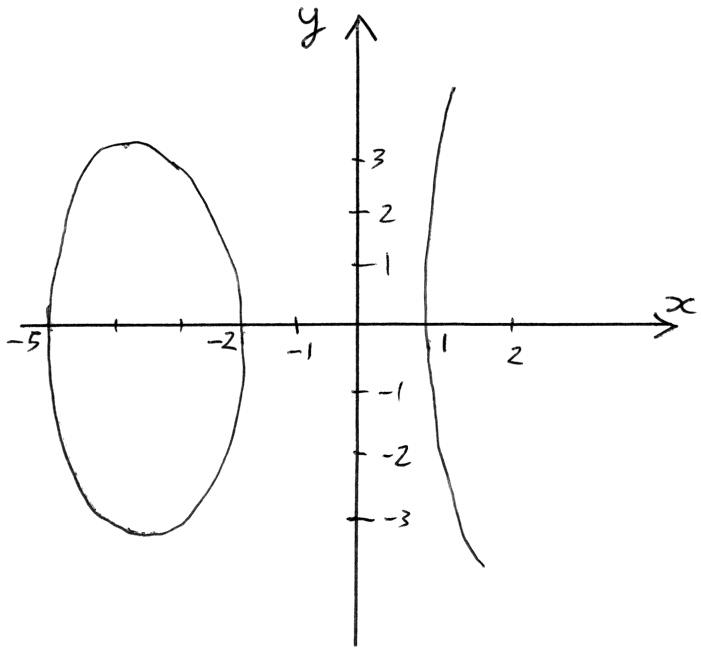 A1A1A1
A1A1A1
Note: Award A1 for shape, A1 for max and for min clearly in correct places, A1 for all intercepts.
Award A1A0A0 if only the complete top half is shown.
[3 marks]
(f) required area is twice that of \(y = f(x)\) between – 5 and – 2 M1A1
answer 14.9 A1 N3
Note: Award M1A0A0 for \(\int_{ – 5}^{ – 2} {f(x){\text{d}}x = 7.47 \ldots } \) or N1 for 7.47.
[3 marks]
Total [14 marks]
Examiners report
This was a multi-part question that was well answered by many candidates. The main difficulty was sketching the graph and this meant that the last part was not well answered.
Question
Find the area of the region enclosed by the curves \(y = {x^3}\) and \(x = {y^2} – 3\) .
▶️Answer/Explanation
Markscheme
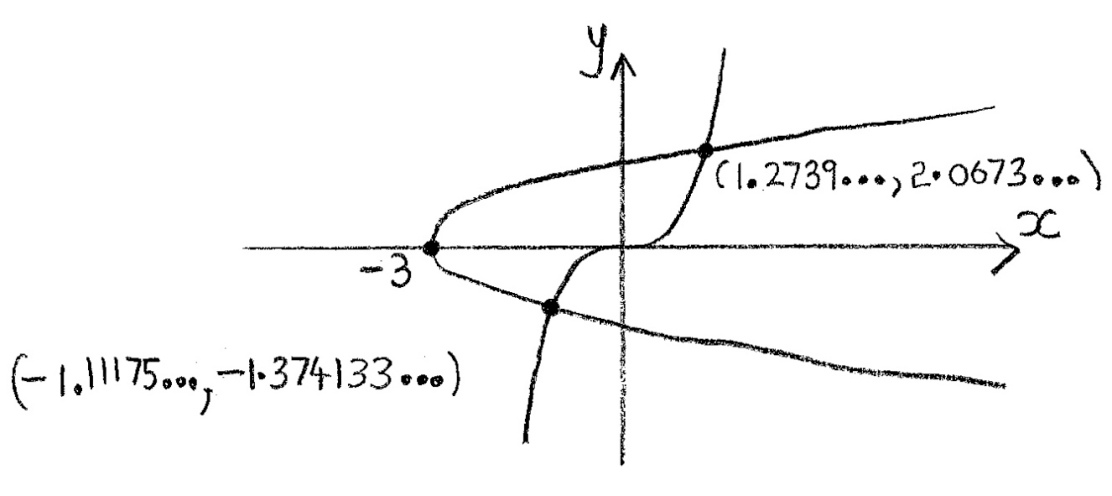
intersection points A1A1
Note: Only either the x-coordinate or the y-coordinate is needed.
EITHER
\(x = {y^2} – 3 \Rightarrow y = \pm \sqrt {x + 3} \,\,\,\,\,\left( {{\text{accept }}y = \sqrt {x + 3} } \right)\) (M1)
\(A = \int_{ – 3}^{ – 1.111…} {2\sqrt {x + 3} \,{\text{d}}x + \int_{ – 1.111…}^{1.2739…} {\sqrt {x + 3} – {x^3}{\text{d}}x} } \) (M1)A1A1
= 3.4595… + 3.8841…
= 7.34 (3sf) A1
OR
\(y = {x^3} \Rightarrow x = \sqrt[3]{y}\) (M1)
\(A = \int_{ – 1.374…}^{2.067…} {\sqrt[3]{y}} – ({y^2} – 3){\text{d}}y\) (M1)A1
= 7.34 (3sf) A2
[7 marks]
Examiners report
This question proved challenging to most candidates. Just a few candidates were able to calculate the exact area between curves. Those candidates who tried to express the functions in terms x of instead of y showed better performances. Determining only \(\sqrt {x + 3} \) was a common error and forming appropriate definite integrals above and below the x-axis proved difficult. Although many candidates attempted to sketch the graphs, many found only one branch of the parabola and only one point of intersection; as the graph of the parabola was not complete, many candidates did not know which area they were trying to find. Not many split the integral correctly to find areas that would add up to the result. Premature rounding was usually seen and consequently final answers proved inaccurate.
Question
Consider the differential equation \(y\frac{{{\text{d}}y}}{{{\text{d}}x}} = \cos 2x\).
a.(i) Show that the function \(y = \cos x + \sin x\) satisfies the differential equation.
(ii) Find the general solution of the differential equation. Express your solution in the form \(y = f(x)\), involving a constant of integration.
(iii) For which value of the constant of integration does your solution coincide with the function given in part (i)?[10]
(i) Determine the equation of C in the form \(y = g(x)\) , and state the range of the function g.
A region R in the xy plane is bounded by C, the x-axis and the vertical lines x = 0 and \(x = \frac{\pi }{2}\).
(ii) Find the area of R.
(iii) Find the volume generated when that part of R above the line y = 1 is rotated about the x-axis through \(2\pi \) radians.[12]
▶️Answer/Explanation
Markscheme
(i) METHOD 1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \sin x + \cos x\) A1
\(y\frac{{{\text{d}}y}}{{{\text{d}}x}} = (\cos x + \sin x)( – \sin x + \cos x)\) M1
\( = {\cos ^2}x – {\sin ^2}x\) A1
\( = \cos 2x\) AG
METHOD 2
\({y^2} = {(\sin x + \cos x)^2}\) A1
\(2y\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2(\cos x + \sin x)(\cos x – \sin x)\) M1
\(y\frac{{{\text{d}}y}}{{{\text{d}}x}} = {\cos ^2}x – {\sin ^2}x\) A1
\( = \cos 2x\) AG
(ii) attempting to separate variables \(\int {y{\text{ d}}y = \int {\cos 2x{\text{ d}}x} } \) M1
\(\frac{1}{2}{y^2} = \frac{1}{2}\sin 2x + C\) A1A1
Note: Award A1 for a correct LHS and A1 for a correct RHS.
\(y = \pm {(\sin 2x + A)^{\frac{1}{2}}}\) A1
(iii) \(\sin 2x + A \equiv {(\cos x + \sin x)^2}\) (M1)
\({(\cos x + \sin x)^2} = {\cos ^2}x + 2\sin x\cos x + {\sin ^2}x\)
use of \(\sin 2x \equiv 2\sin x\cos x\). (M1)
A = 1 A1
[10 marks]
(i) substituting \(x = \frac{\pi }{4}\) and y = 2 into \(y = {(\sin 2x + A)^{\frac{1}{2}}}\) M1
so \(g(x) = {(\sin 2x + 3)^{\frac{1}{2}}}\). A1
range g is \(\left[ {\sqrt 2 ,{\text{ }}2} \right]\) A1A1A1
Note: Accept [1.41, 2]. Award A1 for each correct endpoint and A1 for the correct closed interval.
(ii) \(\int_0^{\frac{\pi }{2}} {{{(\sin 2x + 3)}^{\frac{1}{2}}}{\text{d}}x} \) (M1)(A1)
= 2.99 A1
(iii) \(\pi \int_0^{\frac{\pi }{2}} {(\sin 2x + 3){\text{d}}x – \pi (1)\left( {\frac{\pi }{2}} \right)} \) (or equivalent) (M1)(A1)(A1)
Note: Award (M1)(A1)(A1) for \(\pi \int_0^{\frac{\pi }{2}} {(\sin 2x + 2){\text{d}}x} \)
\( = 17.946 – 4.935{\text{ }}( = \frac{\pi }{2}(3\pi + 2) – \pi \left( {\frac{\pi }{2}} \right))\) A1
Note: Award A1 for \(\pi (\pi + 1)\).
[12 marks]
Examiners report
Part (a) was not well done and was often difficult to mark. In part (a) (i), a large number of candidates did not know how to verify a solution, \(y(x)\), to the given differential equation. Instead, many candidates attempted to solve the differential equation. In part (a) (ii), a large number of candidates began solving the differential equation by correctly separating the variables but then either neglected to add a constant of integration or added one as an afterthought. Many simple algebraic and basic integral calculus errors were seen. In part (a) (iii), many candidates did not realize that the solution given in part (a) (i) and the general solution found in part (a) (ii) were to be equated. Those that did know to equate these two solutions, were able to square both solution forms and correctly use the trigonometric identity \(\sin 2x = 2\sin x\cos x\). Many of these candidates however started with incorrect solution(s).
In part (b), a large number of candidates knew how to find a required area and a required volume of solid of revolution using integral calculus. Many candidates, however, used incorrect expressions obtained in part (a). In part (b) (ii), a number of candidates either neglected to state ‘π’ or attempted to calculate the volume of a solid of revolution of ‘radius’ \(f(x) – g(x)\).
Question
The following graph shows the two parts of the curve defined by the equation \({x^2}y = 5 – {y^4}\), and the normal to the curve at the point P(2 , 1).
a.Show that there are exactly two points on the curve where the gradient is zero.[7]
b.Find the equation of the normal to the curve at the point P.[5]
c.The normal at P cuts the curve again at the point Q. Find the \(x\)-coordinate of Q.[3]
d.The shaded region is rotated by 2\(\pi \) about the \(y\)-axis. Find the volume of the solid formed.[7]
▶️Answer/Explanation
Markscheme
differentiating implicitly: M1
\(2xy + {x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4{y^3}\frac{{{\text{d}}y}}{{{\text{d}}x}}\) A1A1
Note: Award A1 for each side.
if \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) then either \(x = 0\) or \(y = 0\) M1A1
\(x = 0 \Rightarrow \) two solutions for \(y\left( {y = \pm \sqrt[4]{5}} \right)\) R1
\(y = 0\) not possible (as 0 ≠ 5) R1
hence exactly two points AG
Note: For a solution that only refers to the graph giving two solutions at \(x = 0\) and no solutions for \(y = 0\) award R1 only.
[7 marks]
at (2, 1) \(4 + 4\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 4\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{1}{2}\) (A1)
gradient of normal is 2 M1
1 = 4 + c (M1)
equation of normal is \(y = 2x – 3\) A1
[5 marks]
substituting (M1)
\({x^2}\left( {2x – 3} \right) = 5 – {\left( {2x – 3} \right)^4}\) or \({\left( {\frac{{y + 3}}{2}} \right)^2}\,y = 5 – {y^4}\) (A1)
\(x = 0.724\) A1
[3 marks]
recognition of two volumes (M1)
volume \(1 = \pi \int_1^{\sqrt[4]{5}} {\frac{{5 – {y^4}}}{y}} {\text{d}}y\left( { = 101\pi = 3.178 \ldots } \right)\) M1A1A1
Note: Award M1 for attempt to use \(\pi \int {{x^2}} {\text{d}}y\), A1 for limits, A1 for \({\frac{{5 – {y^4}}}{y}}\) Condone omission of \(\pi \) at this stage.
volume 2
EITHER
\( = \frac{1}{3}\pi \times {2^2} \times 4\left( { = 16.75 \ldots } \right)\) (M1)(A1)
OR
\( = \pi \int_{ – 3}^1 {{{\left( {\frac{{y + 3}}{2}} \right)}^2}} {\text{d}}y\left( { = \frac{{16\pi }}{3} = 16.75 \ldots } \right)\) (M1)(A1)
THEN
total volume = 19.9 A1
[7 marks]