Question
Show that \(\int_0^{\frac{\pi }{6}} {x\sin 2x{\text{d}}x = \frac{{\sqrt 3 }}{8} – \frac{\pi }{{24}}} \).
Answer/Explanation
Markscheme
Using integration by parts (M1)
\(u = x{\text{, }}\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1,{\text{ }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = \sin 2x{\text{ and }}v = – \frac{1}{2}\cos 2x\) (A1)
\(\left[ {x\left( { – \frac{1}{2}\cos 2x} \right)} \right]_0^{\frac{\pi }{6}} – \int_0^{\frac{\pi }{6}} {\left( { – \frac{1}{2}\cos 2x} \right){\text{d}}x} \) A1
\( = \left[ {x\left( { – \frac{1}{2}\cos 2x} \right)} \right]_0^{\frac{\pi }{6}} + \left[ {\frac{1}{4}\sin 2x} \right]_0^{\frac{\pi }{6}}\) A1
Note: Award the A1A1 above if the limits are not included.
\(\left[ {x\left( { – \frac{1}{2}\cos 2x} \right)} \right]_0^{\frac{\pi }{6}} = – \frac{\pi }{{24}}\) A1
\(\left[ {\frac{1}{4}\sin 2x} \right]_0^{\frac{\pi }{6}} = \frac{{\sqrt 3 }}{8}\) A1
\(\int_0^{\frac{\pi }{6}} {x\sin 2x{\text{d}}x = \frac{{\sqrt 3 }}{8} – \frac{\pi }{{24}}} \) AG N0
Note: Allow FT on the last two A1 marks if the expressions are the negative of the correct ones.
[6 marks]
Examiners report
This question was reasonably well done, with few candidates making the inappropriate choice of u and \(\frac{{{\text{d}}v}}{{{\text{d}}x}}\). The main source of a loss of marks was in finding v by integration. A few candidates used the double angle formula for sine, with poor results.
Question
Calculate the exact value of \(\int_1^{\text{e}} {{x^2}\ln x{\text{d}}x} \) .
Answer/Explanation
Markscheme
Recognition of integration by parts M1
\(\int {{x^2}\ln x{\text{d}}x = \left[ {\frac{{{x^3}}}{3}\ln x} \right] – \int {\frac{{{x^3}}}{3} \times \frac{1}{x}{\text{d}}x} } \) A1A1
\( = \left[ {\frac{{{x^3}}}{3}\ln x} \right] – \int {\frac{{{x^2}}}{3}{\text{d}}x} \)
\( = \left[ {\frac{{{x^3}}}{3}\ln x – \frac{{{x^3}}}{9}} \right]\) A1
\( \Rightarrow \int_1^{\text{e}} {{x^2}\ln x{\text{d}}x} = \left( {\frac{{{{\text{e}}^3}}}{3} – \frac{{{{\text{e}}^3}}}{9}} \right) – \left( {0 – \frac{1}{9}} \right)\,\,\,\,\,\left( { = \frac{{2{{\text{e}}^3} + 1}}{9}} \right)\) A1
[5 marks]
Question
Find the value of \(\int_0^1 {t\ln (t + 1){\text{d}}t} \).
Answer/Explanation
Markscheme
EITHER
attempt at integration by substitution (M1)
using \(u = t + 1{\text{, d}}u = {\text{d}}t\), the integral becomes
\(\int_1^2 {(u – 1)\ln u{\text{d}}u} \) A1
then using integration by parts M1
\(\int_1^2 {(u – 1)\ln u{\text{d}}u} = \left[ {\left( {\frac{{{u^2}}}{2} – u} \right)\ln u} \right]_1^2 – \int_1^2 {\left( {\frac{{{u^2}}}{2} – u} \right) \times \frac{1}{u}{\text{d}}u} \) A1
\( = – \left[ {\frac{{{u^2}}}{4} – u} \right]_1^2\) (A1)
\( = \frac{1}{4}\,\,\,\,\,\)(accept 0.25) A1
OR
attempt to integrate by parts (M1)
correct choice of variables to integrate and differentiate M1
\(\int_0^1 {t\ln (t + 1){\text{d}}t} = \left[ {\frac{{{t^2}}}{2}\ln (t + 1)} \right]_0^1 – \int_0^1 {\frac{{{t^2}}}{2} \times \frac{1}{{t + 1}}{\text{d}}t} \) A1
\( = \left[ {\frac{{{t^2}}}{2}\ln (t + 1)} \right]_0^1 – \frac{1}{2}\int_0^1 {t – 1 + \frac{1}{{t + 1}}{\text{d}}t} \) A1
\( = \left[ {\frac{{{t^2}}}{2}\ln (t + 1)} \right]_0^1 – \frac{1}{2}\left[ {\frac{{{t^2}}}{2} – t + \ln (t + 1)} \right]_0^1\) (A1)
\( = \frac{1}{4}\,\,\,\,\,\)(accept 0.25) A1
[6 marks]
Examiners report
Again very few candidates gained full marks on this question. The most common approach was to begin by integrating by parts, which was done correctly, but very few candidates then knew how to integrate \(\frac{{{t^2}}}{{t + 1}}\). Those who began with a substitution often made more progress. Again a number of candidates were let down by their inability to simplify appropriately.
Question
The function f is defined on the domain \(\left[ {0,\,\frac{{3\pi }}{2}} \right]\) by \(f(x) = {e^{ – x}}\cos x\) .
State the two zeros of f .
Sketch the graph of f .
The region bounded by the graph, the x-axis and the y-axis is denoted by A and the region bounded by the graph and the x-axis is denoted by B . Show that the ratio of the area of A to the area of B is
\[\frac{{{e^\pi }\left( {{e^{\frac{\pi }{2}}} + 1} \right)}}{{{e^\pi } + 1}}.\]
Answer/Explanation
Markscheme
\({e^{ – x}}\cos x = 0\)
\( \Rightarrow x = \frac{\pi }{2},{\text{ }}\frac{{3\pi }}{2}\) A1
[1 mark]
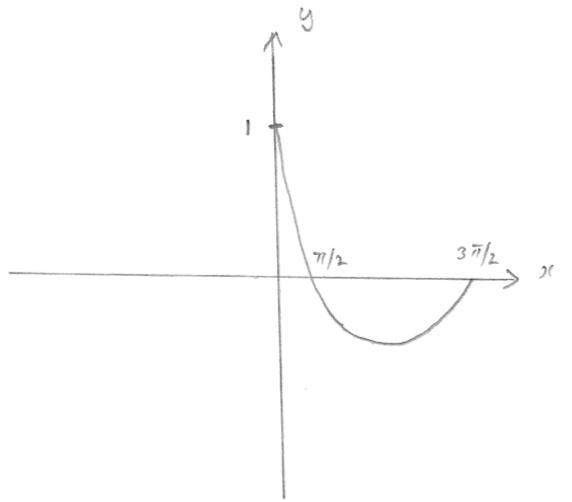 A1
A1
Note: Accept any form of concavity for \(x \in \left[ {0,\frac{\pi }{2}} \right]\).
Note: Do not penalize unmarked zeros if given in part (a).
Note: Zeros written on diagram can be used to allow the mark in part (a) to be awarded retrospectively.
[1 mark]
attempt at integration by parts M1
EITHER
\(I = \int {{{\text{e}}^{ – x}}\cos x{\text{d}}x = – {{\text{e}}^{ – x}}\cos x{\text{d}}x – \int {{{\text{e}}^{ – x}}\sin x{\text{d}}x} } \) A1
\( \Rightarrow I = – {{\text{e}}^{ – x}}\cos x{\text{d}}x – \left[ { – {{\text{e}}^{ – x}}\sin x + \int {{{\text{e}}^{ – x}}\cos x{\text{d}}x} } \right]\) A1
\( \Rightarrow I = \frac{{{{\text{e}}^{ – x}}}}{2}(\sin x – \cos x) + C\) A1
Note: Do not penalize absence of C.
OR
\(I = \int {{{\text{e}}^{ – x}}\cos x{\text{d}}x = {{\text{e}}^{ – x}}\sin x + \int {{{\text{e}}^{ – x}}\sin x{\text{d}}x} } \) A1
\(I = {{\text{e}}^{ – x}}\sin x – {{\text{e}}^{ – x}}\cos x – \int {{{\text{e}}^{ – x}}\cos x{\text{d}}x} \) A1
\( \Rightarrow I = \frac{{{{\text{e}}^{ – x}}}}{2}(\sin x – \cos x) + C\) A1
Note: Do not penalize absence of C.
THEN
\(\int_0^{\frac{\pi }{2}} {{{\text{e}}^{ – x}}\cos x{\text{d}}x = \left[ {\frac{{{{\text{e}}^{ – x}}}}{2}(\sin x – \cos x)} \right]} _0^{\frac{\pi }{2}} = \frac{{{{\text{e}}^{ – \frac{\pi }{2}}}}}{2} + \frac{1}{2}\) A1
\(\int_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} {{{\text{e}}^{ – x}}\cos x{\text{d}}x = \left[ {\frac{{{{\text{e}}^{ – x}}}}{2}(\sin x – \cos x)} \right]_{\frac{\pi }{2}}^{\frac{{3\pi }}{2}} = – \frac{{{{\text{e}}^{ – \frac{{3\pi }}{2}}}}}{2} – \frac{{{{\text{e}}^{ – \frac{\pi }{2}}}}}{2}} \) A1
ratio of A:B is \(\frac{{\frac{{{{\text{e}}^{ – \frac{\pi }{2}}}}}{2} + \frac{1}{2}}}{{\frac{{{{\text{e}}^{ – \frac{{3\pi }}{2}}}}}{2} + \frac{{{{\text{e}}^{ – \frac{\pi }{2}}}}}{2}}}\)
\( = \frac{{{{\text{e}}^{\frac{{3\pi }}{2}}}\left( {{{\text{e}}^{ – \frac{\pi }{2}}} + 1} \right)}}{{{{\text{e}}^{\frac{{3\pi }}{2}}}\left( {{{\text{e}}^{ – \frac{{3\pi }}{2}}} + {{\text{e}}^{ – \frac{\pi }{2}}}} \right)}}\) M1
\( = \frac{{{{\text{e}}^\pi }\left( {{{\text{e}}^{\frac{\pi }{2}}} + 1} \right)}}{{{{\text{e}}^\pi } + 1}}\) AG
[7 marks]
Examiners report
Many candidates stated the two zeros of f correctly but the graph of f was often incorrectly drawn. In (c), many candidates failed to realise that integration by parts had to be used twice here and even those who did that often made algebraic errors, usually due to the frequent changes of sign.
Many candidates stated the two zeros of f correctly but the graph of f was often incorrectly drawn. In (c), many candidates failed to realise that integration by parts had to be used twice here and even those who did that often made algebraic errors, usually due to the frequent changes of sign.
Many candidates stated the two zeros of f correctly but the graph of f was often incorrectly drawn. In (c), many candidates failed to realise that integration by parts had to be used twice here and even those who did that often made algebraic errors, usually due to the frequent changes of sign.
Question
Show that \(\int_1^2 {{x^3}\ln x{\text{d}}x = 4\ln 2 – \frac{{15}}{{16}}} \).
Answer/Explanation
Markscheme
any attempt at integration by parts M1
\(u = \ln x \Rightarrow \frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{x}\) (A1)
\(\frac{{{\text{d}}v}}{{{\text{d}}x}} = {x^3} \Rightarrow v = \frac{{{x^4}}}{4}\) (A1)
\( = \left[ {\frac{{{x^4}}}{4}\ln x} \right]_1^2 – \int_1^2 {\frac{{{x^3}}}{4}{\text{d}}x} \) A1
Note: Condone absence of limits at this stage.
\( = \left[ {\frac{{{x^4}}}{4}\ln x} \right]_1^2 – \left[ {\frac{{{x^4}}}{{16}}} \right]_1^2\) A1
Note: Condone absence of limits at this stage.
\( = 4\ln 2 – \left( {1 – \frac{1}{{16}}} \right)\) A1
\( = 4\ln 2 – \frac{{15}}{{16}}\) AG
[6 marks]
Examiners report
Question
Using integration by parts find \(\int {x\sin x{\text{d}}x} \).
Answer/Explanation
Markscheme
attempt to integrate one factor and differentiate the other, leading to a sum of two terms M1
\(\int {x\sin x{\text{d}}x = x( – \cos x) + } \int {\cos x{\text{d}}x} \) (A1)(A1)
\( = – x\cos x + \sin x + c\) A1
Note: Only award final A1 if \( + {\text{ }}c\) is seen.
[4 marks]
Examiners report
Question
Let \(y = {{\text{e}}^x}\sin x\).
Consider the function \(f\) defined by \(f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi \).
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find an expression for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).
Show that \(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x\).
Show that the function \(f\) has a local maximum value when \(x = \frac{{3\pi }}{4}\).
Find the \(x\)-coordinate of the point of inflexion of the graph of \(f\).
Sketch the graph of \(f\), clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
Find the area of the region enclosed by the graph of \(f\) and the \(x\)-axis.
The curvature at any point \((x,{\text{ }}y)\) on a graph is defined as \(\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}\).
Find the value of the curvature of the graph of \(f\) at the local maximum point.
Find the value \(\kappa \) for \(x = \frac{\pi }{2}\) and comment on its meaning with respect to the shape of the graph.
Answer/Explanation
Answer/Explanation
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)\) M1A1
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x – \sin x)\) M1A1
\( = 2{{\text{e}}^x}\cos x\) AG
[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0\) R1
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0\) R1
hence maximum at \(x = \frac{{3\pi }}{4}\) AG
[2 marks]
\(\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0\) M1
\( \Rightarrow x = \frac{\pi }{2}\) A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
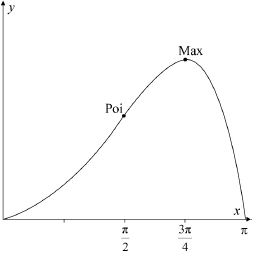
correct shape and correct domain A1
max at \(x = \frac{{3\pi }}{4}\), point of inflexion at \(x = \frac{\pi }{2}\) A1
zeros at \(x = 0\) and \(x = \pi \) A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
\(\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi – \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)} \) A1
OR
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} } \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ – {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi – \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)\) A1
THEN
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x – [{{\text{e}}^x}\cos x]_0^x} \right)} \) M1A1
\(\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)} \) A1
[6 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\) (A1)
\(\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = – \sqrt 2 {e^{\frac{{3\pi }}{4}}}\) (A1)
\(\kappa = \frac{{\left| { – \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}\) A1
[3 marks]
\(\kappa = 0\) A1
the graph is approximated by a straight line R1
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Find \(\int {\arcsin x\,{\text{d}}x} \)
Answer/Explanation
Markscheme
attempt at integration by parts with \(u = \arcsin x\) and \(v’ = 1\) M1
\(\int {\arcsin x\,{\text{d}}x} = x\arcsin x – \int {\frac{x}{{\sqrt {1 – {x^2}} }}{\text{d}}x} {\text{ }}\) A1A1
Note: Award A1 for \(x\arcsin x\) and A1 for \( – \int {\frac{x}{{\sqrt {1 – {x^2}} }}{\text{d}}x} \).
solving \(\int {\frac{x}{{\sqrt {1 – {x^2}} }}{\text{d}}x} \) by substitution with \(u = 1 – {x^2}\) or inspection (M1)
\(\int {\arcsin x{\text{d}}x} = x\arcsin x + \sqrt {1 – {x^2}} + c\) A1
[5 marks]
Examiners report
Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);
Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).
Find \(\int {f(x)\cos x{\text{d}}x} \).
By finding \(g'(x)\) explain why \(g\) is an increasing function.
Answer/Explanation
Markscheme
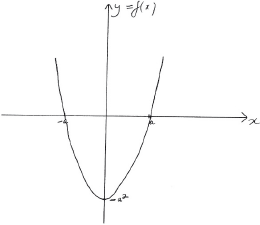
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
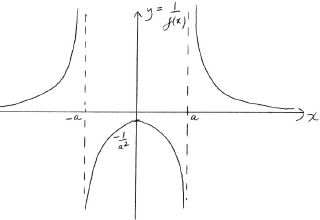
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
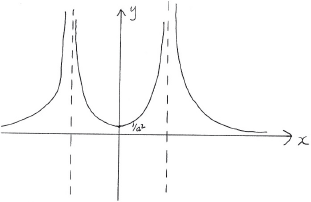
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
Consider the functions \(f,\,\,g,\) defined for \(x \in \mathbb{R}\), given by \(f\left( x \right) = {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) and \(g\left( x \right) = {{\text{e}}^{ – x}}\,{\text{cos}}\,x\).
Find \(f’\left( x \right)\).
Find \(g’\left( x \right)\).
Hence, or otherwise, find \(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} \).
Answer/Explanation
Markscheme
attempt at product rule M1
\(f’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + {{\text{e}}^{ – x}}\,{\text{cos}}\,x\) A1
[2 marks]
\(g’\left( x \right) = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – {{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
[1 mark]
METHOD 1
Attempt to add \(f’\left( x \right)\) and \(g’\left( x \right)\) (M1)
\(f’\left( x \right) + g’\left( x \right) = – 2{{\text{e}}^{ – x}}\,{\text{sin}}\,x\) A1
\(\int\limits_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x} = \left[ { – \frac{{{{\text{e}}^{ – x}}}}{2}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)} \right]_0^\pi \) (or equivalent) A1
Note: Condone absence of limits.
\( = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)\) A1
METHOD 2
\(I = \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\( = – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) OR \( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x + \int {{{\text{e}}^{ – x}}} \,{\text{cos}}\,x\,{\text{d}}x\) M1A1
\( = – {{\text{e}}^{ – x}}\,{\text{sin}}\,x – {{\text{e}}^{ – x}}\,{\text{cos}}\,x – \int {{{\text{e}}^{ – x}}} \,{\text{sin}}\,x\,{\text{d}}x\)
\(I = \frac{1}{2}{{\text{e}}^{ – x}}\left( {{\text{sin}}\,x + {\text{cos}}\,x} \right)\) A1
\(\int_0^\pi {{{\text{e}}^{ – x}}\,{\text{sin}}\,x\,{\text{d}}x = \frac{1}{2}\left( {1 + {{\text{e}}^{ – \pi }}} \right)} \) A1
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Find the value of the integral \(\int_0^{\sqrt 2 } {\sqrt {4 – {x^2}} {\text{d}}x} \) .
Find the value of the integral \(\int_0^{0.5} {\arcsin x {\text{d}}x} \) .
Using the substitution \(t = \tan \theta \) , find the value of the integral
\[\int_0^{\frac{\pi }{4}} {\frac{{{\text{d}}\theta }}{{3{{\cos }^2}\theta + {{\sin }^2}\theta }}} {\text{ }}.\]
Answer/Explanation
Markscheme
let \(x = 2\sin \theta \) M1
\({\text{d}}x = 2\cos \theta {\text{d}}\theta \) A1
\(I = \int_0^{\frac{\pi }{4}} {2\cos \theta \times 2\cos \theta {\text{d}}\theta \,\,\,\,\,\left( { = 4\int_0^{\frac{\pi }{4}} {{{\cos }^2}\theta {\text{d}}\theta } } \right)} \) A1A1
Note: Award A1 for limits and A1 for expression.
\( = 2\int_0^{\frac{\pi }{4}} {(1 + \cos 2\theta ){\text{d}}\theta } \) A1
\( = 2\left[ {\theta + \frac{1}{2}\sin 2\theta } \right]_0^{\frac{\pi }{4}}\) A1
\( = 1 + \frac{\pi }{2}\) A1
[7 marks]
\(I = [x\arcsin x]_0^{0.5} – \int_0^{0.5} {x \times \frac{1}{{\sqrt {1 – {x^2}} }}{\text{d}}x} \) M1A1A1
\( = [x\arcsin x]_0^{0.5} + \left[ {\sqrt {1 – {x^2}} } \right]_0^{0.5}\) A1
\( = \frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} – 1\) A1
[5 marks]
\({\text{d}}t = {\sec ^2}\theta {\text{d}}\theta {\text{ , }}\left[ {0,\frac{\pi }{4}} \right] \to [0,{\text{ 1]}}\) A1(A1)
\(I = \int_0^1 {\frac{{\frac{{{\text{d}}t}}{{(1 + {t^2})}}}}{{\frac{3}{{(1 + {t^2})}} + \frac{{{t^2}}}{{(1 + {t^2})}}}}} \) M1(A1)
\( = \int_0^1 {\frac{{{\text{d}}t}}{{3 + {t^2}}}} \) A1
\( = \frac{1}{{\sqrt 3 }}\left[ {\arctan \left( {\frac{x}{{\sqrt 3 }}} \right)} \right]_0^1\) A1
\( = \frac{\pi }{{6\sqrt 3 }}\) A1
[7 marks]
Examiners report
[N/A]
[N/A]
[N/A]
MAA HL 5.17 INTEGRATION BY PARTS-Neha
Question
Find \(I_{1}=\int 2xe^{x} dx\), \( I_{2}=\int 2x\cos xdx\), \(I_{3}=\int 2x\sin xdx\), \( I_{4}=\int 2x\) \(ln\) \(xdx\)
Answer/Explanation
Ans
\(I_{1}=2\left ( x-1 \right )e^{x}+c\),
\(I_{2}=2x\sin x+2\cos x+c\),
\(I_{3}=2\sin x-2x\cos x+c\),
\(I_{4}=x^{2}\ln x-\frac{x^{2}}{2}+c\)
Question
Find \(I_{1}=\int \left ( 3x^{2}+4x+1 \right )cos\) \(xdx\), \( I_{2}=\int \left ( 3x^{2}+4x+1 \right )ln\) \(xdx\)
Answer/Explanation
Ans
\(I_{1}=\left ( 3x^{2}+4x-5 \right )\sin x+\left ( 6x+4 \right )\cos x+c\),
\(I_{2}=\left ( x^{3}+2x^{2}+x \right )\\ln x-\frac{x^{2}}{3}-x^{2}- x+c\)
Question
Find \(\int e^{2x}cos\) \(2xdx\) by using integration by parts in two different ways:
(a) by integrating \(e^{2x}\) first (b) by integrating cos 2x first
Answer/Explanation
Ans
\(\frac{e^{2x}\left ( \sin2x+\cos2x \right )}{4}+c\)
Question
Let \(I_{n}=\int x^{n}e^{x}dx\).
(a) Find \(I_{0}\)
(b) Express \(I_{n}\) in terms of \(I_{n-1}\)
(c) Find \(I_{1}\), \(I_{2}\) and \(I_{3}\) by using the recursive relation found in (b)
Answer/Explanation
Ans
Let \(I_{n}=\int x^{n}e^{x}dx.\)
(a) \(I_{0}=e^{x}+c\)
(b) \(I_{n}=x^{n}e^{x}-nI_{n-1}\)
(c) \(I_{1}=xe^{x}-e^{x}+c\),
\(I_{2}=x^{2}e^{x}-2(xe^{x}-e^{x})+c=\left ( x^{2}-2x+2 \right )e^{x}+c\),
\(I_{3}=x^{3}e^{x}-3(x^{2}-2x+2)e^{x}+c=\left ( x^{3}-3x^{2}+6x-6 \right )e^{x}+c\)
Question
Consider \(I=\int 4sin x\cos xdx\)
(a) Find I by using the substitution u = sin x
(b) Find I by using the substitution u = cos x
(c) Find I by using the double angle formula for sin2θ
(d) Find I by using integration by parts
(e) Explain the difference in the results
Answer/Explanation
Ans
\(I=\int 4\sin x\cos xdx=-2\cos ^{2}x+c=2\sin x+c=-\cos 2x+c\)
The results differ by a constant (which is incorporated in c)
Question
Let \(A_{n}=\int x^{n}\sin xdx\) and \(B_{n}=\int x^{n}\cos xdx\)
(a) Find \(A_{0}\) and \(B_{0}\)
(b) Express \(A_{n}\) in terms of \(B_{n-1}\) by using integration by parts.
(c) Express \(B_{n}\) in terms of \(A_{n-1}\) by using integration by parts.
(d) Hence express \(A_{n}\) in terms of \(A_{n-2}\)
(e) Find \(A_{1}\), \(A_{1}\) and \(A_{3}\) by using the results above.
Answer/Explanation
Ans
(a) \(A_{0}=-\cos x+c\) and \(B_{0}=\sin x+c\)
(b) \(A_{n}=-x^{n}\cos x+nB_{n-1}\)
(c) \(B_{n}=-x^{n}\sin x+nA_{n-1}\)
(d) \(A_{n}=-x^{n}\cos x+n\left [ x^{n-1}\sin x+(n-1)A_{n-2}\right ]\)
\(=-x^{n}\cos x+nx^{n-1}\sin x+n(n-1)A_{n-2}\)
(e) \(A_{1}=-x\cos x+\sin x+c\),
\(A_{2}=-x^{2}\cos x+2x\sin x-2\cos x+c\),
\(A_{3}=-x^{3}\cos x+3x^{2}\sin x+6\left [ -x^{2}\cos x+2x\sin x-2\cos x \right ]+c\)
Question
Let (I_{n}=\int \sin ^{n}xdx\)
(a) Find \(I_{0}\) and \(I_{1\)}
(b) Express \(I_{n}\) in terms of \(I_{n-2}\) by using integration by parts
(c) Find \(I_{2}\), \(I_{3}\), \(I_{4}\), \(I_{5}\)by using recursive relation found in (b).
(d) Find \(I_{2}\),\(I_{4}\) by using the double angle formula \(\sin ^{2}x=\frac{1-\cos 2x}{2}\).
(e) Find \(I_{3}\), \(I_{5}\) by using the substitution \(u=cosx\)
Answer/Explanation
Ans
(a) \(I_{0}=x+c\) and \(I_{1}=-\cos x+c\)
(b) \(I_{n}=-\sin ^{n-1}x\cos x+(n-1)\int \sin^{n-2}x\cos^{2}xdx\)
\(=-\sin ^{n-1}x\cos x+(n-1)\int \sin^{n-2}x(1-\sin^{2}x)dx\)
\(=-\sin ^{n-1}x\cos x+(n-1)I_{n-2}-(n-1)I_{n}\)
Hence, \(I_{n}=-\frac{1}{n}\sin^{n-1}x\cos x+\frac{n-1}{n}I_{n-2}\)
(c) \(I_{2}=-\frac{1}{2}\sin x\cos x+\frac{x}{2}+c\)
\(I_{3}=-\frac{1}{3}\sin^{2} x\cos x-\frac{2}{3}\cos x+c\)
\(I_{4}=-\frac{1}{4}\sin^{3} x\cos x-\frac{3}{8}\sin x\cos x+\frac{3x}{8}+c\)
\(I_{5}=-\frac{1}{5}\sin^{4} x\cos x-\frac{4}{15}\cos^{3} x+\frac{4}{5}\cos x+c\)
(d) \(I_{2}=-\frac{1}{2}\sin x\cos x+\frac{x}{2}+c\)
\(I_{4}=-\frac{\sin 4x}{32}-\frac{\sin 2x}{8}+c\)
(e) \(I_{3}=\frac{1}{3}cos^{3} x-\cos x+c\)
\(I_{5}=-\frac{\cos^{5}x}{5}-\frac{2\cos^{3} x}{3}-\cos x+c\)
Question
Find \(\int \left (\theta cos\theta-\theta \right )d\theta \)
Answer/Explanation
Ans
Using integration by parts
\(u=\theta\) \(v=\sin \theta\)
\(du=d\theta\) \(dv=\cos \theta d\theta\)
\(\Rightarrow \int \theta \cos \theta d\theta =\theta \sin \theta-\int \sin \theta d\theta\)
\(\Rightarrow \int \theta \cos \theta d\theta =\theta \sin \theta+cos\theta\)
\(Therefore, \Rightarrow \int (\theta \cos \theta -\theta)d\theta = \theta \sin \theta +\cos -\frac{\theta ^{2}}{2}+c\)
Question
Find \(\int \frac{ln}{\sqrt{x}}dx\)
Ans
\(\int \frac{\ln x}{\sqrt{x}}dx=\int u\frac{dv}{dx}=\int \ln xd\frac{(2x\frac{1}{2})}{dx}dx\)
\(= 2x^{\frac{1}{2}}\ln x-2\int x^{\frac{1}{2}}\times \frac{1}{x}dx=2x^{\frac{1}{2}}\ln x-2\int \frac{1}{\sqrt{x}}dx\)
\(= 2x^{\frac{1}{2}}\ln x-4x\frac{1}{2}+C\)
10. Find \(\int e^{x}\cos xdx\)
Answer/Explanation
Ans
\(\int e^{x}\cos xdx=e^{x}\cos x+\int e^{x} \sin xdx\)
\(=e^{x}\cos x+e^{x} \sin x-\int e^{x}\cos xdx\)
\(2\int e^{x}\cos xdx=e^{x}(\cos x+\sin x)+c\)
\(\int e^{x}\cos xdx=\frac{e^{x}}{2}(\cos x+\sin x)+k\)
Question
Find \(\int e^{2x}\sin xdx\)
Answer/Explanation
Ans
METHOD 1
\(\int e^{2x}\sin xdx=-e^{2x}\cos x+2\int e^{2x} \cos xdx\)
\(= -e^{2x}\cos x+2(e^{2x}\sin x)- 2\int e^{2x} \sin xdx\)
\(= -e^{2x}\cos x+2e^{2x}\sin x- 4\int e^{2x} \sin xdx\)
\(\Rightarrow 5\int e^{2x}\sin xdx=e^{2x}\left ( 2\sin x-\cos x\right )\)
\(\int e^{2x}\sin xdx=\frac{e^{2x}}{5}(2\sin x-\cos x)\) + C
METHOD 2
\(\int e^{2x}\sin xdx=\frac{1}{2}e^{2x}\sin x-\frac{1}{2}\int e^{2x}\cos xdx\)
\(= \frac{1}{2}e^{2x}\sin x-\frac{1}{4}\int e^{2x}\cos x-\frac{1}{4}\int e^{2x}\sin xdx\)
\(= \frac{5}{4}\int e^{2x}\sin xdx=\frac{1}{2}\int e^{2x}\sin x-\frac{1}{4}\int e^{2x}\cos x\)
\(\int e^{2x}\sin xdx=\frac{e^{2x}}{5}(2\sin x-\cos x)+C\)
Question
Let \(f(x)=x\ln x-x, x> 0\)
(a) Find \(f'(x)\). (b) Using integration by parts find \(\int \left ( \ln x \right )^{2}dx\)
[ Suggestion: use two different methods for (b): look at the integral
(i) as \(\int 1.(\ln x)^{2}dx\)
(ii) as \(\int (\ln x).(\ln x)dx\)
Answer/Explanation
Ans
(a) \(f'(x)=\ln x+\frac{1}{x}-1=\ln x\)
(b) Using integration by parts
METHOD 1
\(\int \left ( \ln x\right )^{2}dx=\left ( \ln x\right )^{2}.\ x-\int x.\ \frac{2}{x}\left ( \ln x\right )dx\)
\(=x\left ( \ln x\right )^{2}-2\int \left ( \ln x\right )dx\)
\(=x\left ( \ln x\right )^{2}-2\left ( x\ln x-x \right )+C\)
\((=x\left ( \ln x\right )^{2}-2x\ln x+2x+C)\)
METHOD 2
\(\int \left ( \ln x\right )^{2}dx =x\left ( \ln x \right )^{2}-x\ln x-\int \left ( \ln x-1 \right )dx\)
\(= x\left ( \ln x \right )^{2}-x\ln x-\left ( x\ln x-x-x \right )+C\)
\((= x\left ( \ln x \right )^{2}-2x\ln x+2x+C)\)
Question
(a) Use integration by parts to find \(\int x^{2}\ln xdx\). (b) Evaluate \(\int_{1}^{2}x^{2}\ln xdx\)
Answer/Explanation
Ans
(a) \(\int x^{2}\ln xdx=\left [ \frac{x^{3}}{3}\ln x \right ]-\int \frac{x^{3}}{3}\frac{1}{x}dx\)
\(=\frac{x^{3}}{3}\ln x-\frac{x^{3}}{9}\) (Constant of integration not required.)
(b) \(\int_{1}^{2}x^{2}\ln xdx=1.07\) \(\left ( or \frac{8}{3}\ln 2-\frac{7}{9} \right )\)
Question
Calculate the exact value of \(\int_{1}^{e}x^{5}\ln xdx\)
Answer/Explanation
Ans
Recognition of integration by parts
\(\int_{1}^{e}x^{5}\ln xdx=\left [ \frac{x^{6}}{6}\ln x \right ]_{1}^{e}-\int_{1}^{e}\frac{x^{6}}{6}\frac{1}{x}dx\)
\(=\left [ \frac{x^{6}}{6}\ln x \right ]_{1}^{e}-\int_{1}^{e}\frac{x^{5}}{6}dx=\left [ \frac{x^{6}}{6}\ln x \right ]_{1}^{e}-\left [ \frac{x^{6}}{36}\right ]_{1}^{e}\)
\(=\left ( \frac{e^{6}}{6} \right )-\frac{e^{6}}{36}+\frac{1}{36}\left ( =\frac{5e^{6}+1}{36} \right )\)
Question
Show that \(\int_{0}^{\frac{\pi }{6}}x\sin 2xdx=\frac{\sqrt{3}}{8}-\frac{\pi}{24}\)
Answer/Explanation
Ans
Using integration by parts
\(u=x,\frac{\mathrm{d} u}{\mathrm{d} x}=1\sin 2x\) and \(v=-\frac{1}{2}\cos 2x\)
\(\left [ x\left ( -\frac{1}{2}\cos 2x \right ) \right ]_{0}^{\frac{\pi }{6}}-\int_{0}^{\frac{\pi }{6}} \left (-\frac{1}{2} \cos 2x \right )dx\)
\(=\left [ x\left ( -\frac{1}{2}\cos 2x \right ) \right ]_{0}^{\frac{\pi}{6}}+\left [ \frac{1}{4}\sin 2x \right ]_{0}^{\frac{\pi}{6}}\)
\(\left [ x\left ( -\frac{1}{2}\cos 2x \right ) \right ]_{0}^{\frac{\pi}{6}}=-\frac{\pi }{24}\)
\(\left [ \frac{1}{4}\sin 2x \right ]_{0}^{\frac{\pi}{6}}=\frac{\sqrt{3}}{8}\)
\(\int_{0}^{\frac{\pi }{6}}x\sin 2xdx\)=\(\frac{\sqrt{3}}{8}-\frac{\pi }{24}\)
Question
Find \(\int_{0}^{a}arc\sin xdx, 0<a<1\)
Answer/Explanation
Ans
\(\int_{0}^{a}arc\sin xdx=\ xarc\sin x\ _{0}^{a}-\int_{0}^{a}\frac{x}{\sqrt{1-x^{2}}}dx\)
=\(\ a\ arc\sin a-0\left [ \sqrt{1-x^{2}} \right ]_{0}^{a}\)
=\(\ a\ arc\sin a+\sqrt{1-a^{2}}-1\)
Question
The region bounded by the curve \(y=\frac{\ln \left ( x \right )}{x}\) and the lines x = 1, x = e , y = 0 is rotated through 2π radians about the x-axis. Find the volume of the solid generated.
Answer/Explanation
Ans
METHOD 1
\(V=\pi \int_{1}^{e}\left ( \frac{\ln x}{x} \right )^{2}dx\)
Integrating by parts:
\(u=\left ( \ln x^{2} \right ),\frac{\mathrm{d} v}{\mathrm{d} x}=\frac{1}{x^{2}}\)
\(\frac{\mathrm{d} u}{\mathrm{d} x}=\frac{2\ln x}{x},\ v=-\frac{1}{x}\)
\(\Rightarrow V=\pi \left ( -\frac{\left ( \ln x \right )^{2}}{x} \right )+2\int \frac{\ln x}{x^{2}}dx\)
\(u=\ln x, \frac{\mathrm{d} v}{\mathrm{d} x}=\frac{1}{x^{2}}\)
\(\frac{\mathrm{d} u}{\mathrm{d} x}=\frac{1}{x},v=-\frac{1}{x}\)
\(\therefore \int \frac{\ln x}{x^{2}}dx =-\frac{\ln x}{x}+\int \frac{1}{x^{2}}dx=-\frac{\ln x}{x}-\frac{1}{x}\)
\(\therefore V=\pi\left [ -\frac{\left ( \ln x \right )^{2}}{x} +2\left ( -\frac{\ln x}{x}-\frac{1}{x}\right )\right]_{1}^{0}\)
\(=2\pi -\frac{5\pi }{e}\)
METHOD 2
\(V=\pi \int_{1}^{e}\left ( \frac{\ln x}{x} \right )^{2}dx\)
Let \(\ln x=u\Rightarrow x=e^{u},\frac{\mathrm{d} x}{\mathrm{x}}=du\)
\(\int \left ( \frac{\ln x}{x} \right )^{2}dx=\int \frac{u^{2}}{e^{u}}du=\int e^{-u}u^{2}du=-e^{-u}u^{2}+2\int e^{-u}u\ du\)
\(=-e^{-u}u^{2}+2\left ( -e^{-u}u +\int -e^{-u}du \right )=-e^{-u}u^{2}-2e^{-u}u-2e^{-u}\)
\(=-e^{-u}(u^{2}+2u+2)\)
When \(x=e,u=1\). When \(x=1,u=0\).
\(\therefore\) Volume =\(\pi \left [ -e^{-u}(u^{2}+2u+2) \right ]_{0}^{1}\)
\(=\pi (-5e^{-1}+2)\left ( =2\pi -\frac{5\pi }{e} \right )\)
Extra Question
Find the area of the region described above
Ans
The area is \(\int_{1}^{e}\frac{\ln x}{x}dx\)
The indefinite integral \(\int\frac{\ln x}{x}dx\) can be found either by substitution or by integration by parts.
\(\int\frac{\ln x}{x}dx=\frac{(\ln x)^{2}}{2}+c\), thus the area is \(\left [\frac{(\ln x)^{2}}{2} \right ]_{1}^{e}=\frac{1}{2}\)
Question
This is a table from my lecture notes. Please make sure that you can solve all the examples and the theoretical questions in columns 2 and 3.
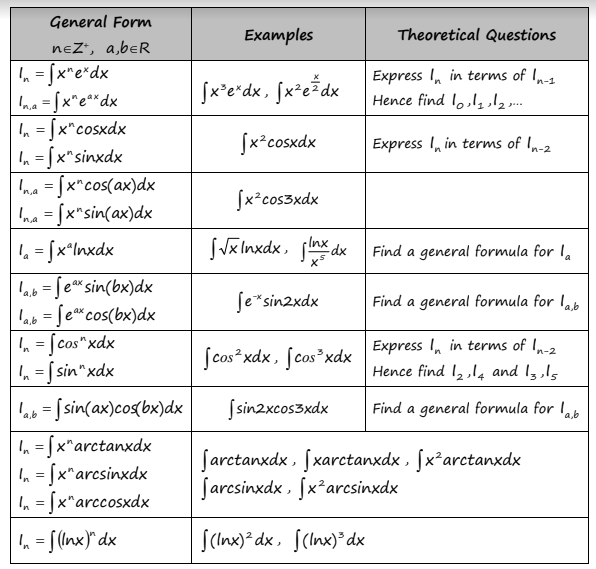
Answer/Explanation
Ans
Theoretical
Question
Let \(f(x)=x\cos 3x.\)
(a) Use integration by parts to show that
\(\int f(x)dx=\frac{1}{3}x\sin 3x+\frac{1}{9}\cos 3x+c\)
(b) Use your answer to part (a) to calculate the exact area enclosed by f(x) and the x-axis in each of the following cases. Give your answers in terms of π.
(i) \(\frac{\pi }{6}\leq x\leq \frac{3\pi}{6}\) (ⅱ) \(\frac{3\pi }{6}\leq x\leq \frac{5\pi}{6}\) (ⅲ) \(\frac{5\pi }{6}\leq x\leq \frac{7\pi}{6}\)
(c) Given that the above areas are the first three terms of an arithmetic sequence, find an expression for the total area enclosed by f(x) and the x-axis for
\(\frac{\pi }{6}\leq x\leq \frac{\left ( 2n+1 \right )\pi}{6}\), where n \(\epsilon\) Z. Give your answers in terms of n and π.
Answer/Explanation
Ans
(a) \(\int x\cos 3\ xdx=\frac{1}{3}x\sin 3x-\frac{1}{3}\int \sin 3\ xdx\)
\(\frac{1}{3}x\sin 3x+\frac{1}{9}\cos 3x+C\) (not required)
(b) (i) Area= \(\left | \left [ \frac{1}{3}x\sin 3x+\frac{1}{9}\cos 3x \right ]_{\frac{\pi }{6}}^{\frac{3\pi }{6}} \right |=\frac{2\pi }{9}\)
(ii) Area= \(\left | \left [ \frac{1}{3}x\sin 3x+\frac{1}{9}\cos 3x \right ]_{\frac{\pi }{6}}^{\frac{5\pi }{6}} \right |=\frac{4\pi }{9}\)
(iii) Area= \(\left | \left [ \frac{1}{3}x\sin 3x+\frac{1}{9}\cos 3x \right ]_{\frac{5\pi }{6}}^{\frac{7\pi }{6}} \right |=\frac{6\pi }{9}\)
Note: Accept negative answers for part (b), as long as they are exact.
Do not accept answers found using a calculator.
(c) The above areas form an A.S. with \(u_{1}=\frac{2\pi }{9}\) and \(d=\frac{2\pi }{9}\)
The required area = \(S_{n}=\frac{n}{2}\left [ \frac{4\pi }{9}+\frac{2\pi }{9}(n-1) \right ]=\frac{n\pi }{9}(n+1)\)