IBDP Maths analysis and approaches Topic: AHL 5.16 Integration by parts HL Paper 2

prove that \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + n{\left( {\frac{1}{2}} \right)^{n – 1}} = 4 – \frac{{n + 2}}{{{2^{n – 1}}}}\)

for n = 1

\({\text{LHS}} = 1,{\text{ RHS}} = 4 – \frac{{1 + 2}}{{{2^0}}} = 4 – 3 = 1\)

so true for n = 1     R1

assume true for n = k     M1

so \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + k{\left( {\frac{1}{2}} \right)^{k – 1}} = 4 – \frac{{k + 2}}{{{2^{k – 1}}}}\)

now for n = k +1

LHS: \(1 + 2\left( {\frac{1}{2}} \right) + 3{\left( {\frac{1}{2}} \right)^2} + 4{\left( {\frac{1}{2}} \right)^3} + … + k{\left( {\frac{1}{2}} \right)^{k – 1}} + (k + 1){\left( {\frac{1}{2}} \right)^k}\)     A1

\( = 4 – \frac{{k + 2}}{{{2^{k – 1}}}} + (k + 1){\left( {\frac{1}{2}} \right)^k}\)     M1A1

\( = 4 – \frac{{2(k + 2)}}{{{2^k}}} + \frac{{k + 1}}{{{2^k}}}\,\,\,\,\,\)(or equivalent)     A1

\( = 4 – \frac{{(k + 1) + 2}}{{{2^{(k + 1) – 1}}}}\,\,\,\,\,\)(accept \(4 – \frac{{k + 3}}{{{2^k}}}\))     A1

Therefore if it is true for n = k it is true for n = k + 1. It has been shown to be true for n = 1 so it is true for all \(n{\text{ }}( \in {\mathbb{Z}^ + })\).     R1

Note: To obtain the final R mark, a reasonable attempt at induction must have been made.

[8 marks]

(a)

METHOD 1

\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = – \cos x{{\text{e}}^{2x}} + \int {2{{\text{e}}^{2x}}\cos x{\text{d}}x} } \)     M1A1A1

\( = – \cos x{{\text{e}}^{2x}} + 2{{\text{e}}^{2x}}\sin x – \int {4{{\text{e}}^{2x}}\sin x{\text{d}}x} \)     A1A1

\(5\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = – \cos x{{\text{e}}^{2x}} + 2{{\text{e}}^{2x}}\sin x} \)     M1

\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + C} \)     AG 

METHOD 2

\(\int {\sin x{{\text{e}}^{2x}}{\text{d}}x = \frac{{\sin x{{\text{e}}^{2x}}}}{2} – \int {\cos x\frac{{{{\text{e}}^{2x}}}}{2}{\text{d}}x} } \)     M1A1A1

\( = \frac{{\sin x{{\text{e}}^{2x}}}}{2} – \cos x\frac{{{{\text{e}}^{2x}}}}{4} – \int {\sin x\frac{{{{\text{e}}^{2x}}}}{4}{\text{d}}x} \)     A1A1

\(\frac{5}{4}\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{{{{\text{e}}^{2x}}\sin x}}{2} – \frac{{\cos x{{\text{e}}^{2x}}}}{4}} \)     M1

\(\int {{{\text{e}}^{2x}}\sin x{\text{d}}x = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + C} \)     AG

[6 marks]

(b)

\(\int {\frac{{{\text{d}}y}}{{\sqrt {1 – {y^2}} }} = \int {{{\text{e}}^{2x}}\sin x{\text{d}}x} } \)     M1A1

\(\arcsin y = \frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x)( + C)\)     A1

when \(x = 0,{\text{ }}y = 0 \Rightarrow C = \frac{1}{5}\)     M1

\(y = \sin \left( {\frac{1}{5}{{\text{e}}^{2x}}(2\sin x – \cos x) + \frac{1}{5}} \right)\)     A1

[5 marks]

(c)

(i) 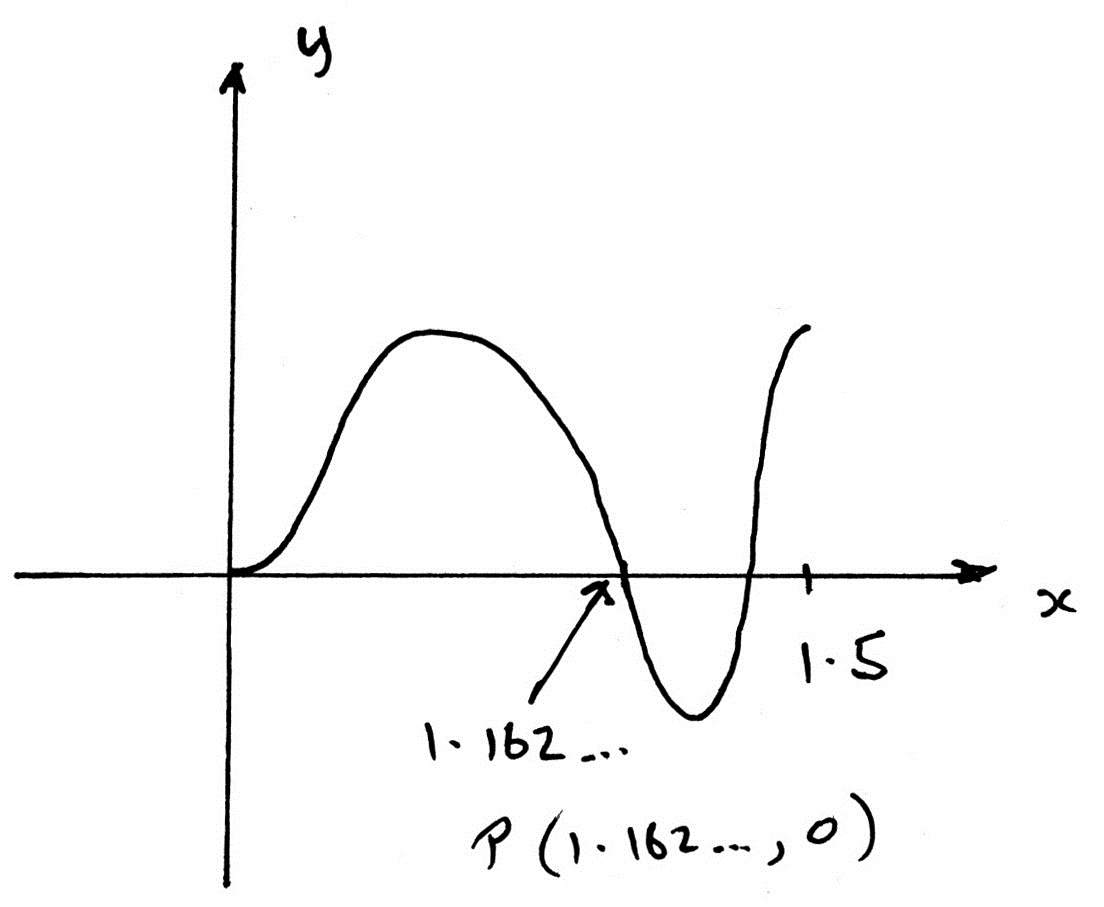        A1

P is (1.16, 0)     A1

Note: Award A1 for 1.16 seen anywhere, A1 for complete sketch.

Note: Allow FT on their answer from (b)

(ii)     \(V = \int_0^{1.162…} {\pi {y^2}{\text{d}}x} \)     M1A1

\( = 1.05\)     A2

Note: Allow FT on their answers from (b) and (c)(i).

[6 marks]