▶️Answer/Explanation
Question
(a) Calculate \(\int \frac{1}{5+x^{2}}dx\) , by using the substitution \(x=\sqrt{5}\, \textup{tan}\, \theta \)
(b) Calculate (i) \(\int \frac{1}{\sqrt{5-x^{2}}}dx\) , (ii) \(\int \sqrt{5-x^{2}\, dx}\) by using the substitution \(x=\sqrt{5}\, \textup{sin}\, \theta \)
▶️Answer/Explanation
Ans
(a) \(\frac{1}{\sqrt{5}}\textup{arctan}\frac{x}{\sqrt{5}}+c\) (b) (i) \(\textup{arcsin}\frac{x}{\sqrt{5}}+c\) , (ii) \(\frac{5}{2}\textup{arcsin}\frac{x}{\sqrt{5}}+\frac{x\sqrt{5-x^{2}}}{2}+c\)
Question
Calculate \(\int \sqrt{\frac{x}{4-x}}dx\) , by using the substitution \(x=4\, \textup{sin}^{2}\, \theta \)
Express your answer in the form \(A\, \textup{arcsin}\frac{\sqrt{x}}{2}+B\sqrt{4x-x^{2}}+c\)
▶️Answer/Explanation
Ans
\(4\, \textup{arcsin}\frac{\sqrt{x}}{2}-\sqrt{4x-x^{2}}+c\)
Question
(a) Show that \(\frac{2x+4}{(x^{2}+4)(x-2)}=\frac{1}{x-2}-\frac{x}{x^{2}+4}\)
(b) Hence find \(\int \frac{2x+4}{(x^{2}+4)(x-2)}dx\)
▶️Answer/Explanation
Ans
(b) \(\textup{In}(x-2)-\frac{1}{2}\textup{In}(x^{2}+4)+c\)
Question
Using the substitution \(y=2-x\), or otherwise, find \(\int \left ( \frac{x}{2-x} \right )^{2}dx\). (Total 6 marks)
▶️Answer/Explanation
Ans
\(I=\int \left ( \frac{2-y}{y} \right )^{2}(-dy)\) (M1)(A1)
\(=\int \left ( \frac{4}{y^{2}}-\frac{4}{y}+1 \right )\textup{d}y=\frac{4}{y}+4\, \textup{In}\left | y \right |-y+c\) (A1)(A1)(A1)
\(=\frac{4}{2-x}+4\textup{In}\left | 2-x \right |-(2-x)+c\) (A1) (C6)
Note: c and modulus signs not required. [6]
Question
Using the substitution \(u=\frac{1}{2}x+1\),or otherwise, find the integral \(\int x\sqrt{\frac{1}{2}x+1}\: dx\). (Total 4 marks)
▶️Answer/Explanation
Ans
Let \(u=\frac{1}{2}x+1\Leftrightarrow x=2(u-1)\Rightarrow \frac{\textup{d}x}{\textup{d}u}=2\)
Then \(\int x\left ( \frac{1}{2}x+1 \right )^{1/2}dx\)
\(=\int 2(u-1)\times u^{1/2}\times 2\textup{d}u\) (M1)
\(=4\int (u^{3/2}-u^{1/2})\textup{d}u\) (A1)
\(=4\left [ \frac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2} \right ]+C\) (M1)
\(=4\left [ \frac{2}{5}\left ( \frac{1}{2}x+1 \right )^{5/2}-\frac{2}{3}\left ( \frac{1}{2}x+1 \right )^{3/2} \right ]+C\) (A1) [4]
Question
Use the substitution \(u=x+2\) to find \(\int \frac{x^{3}}{(x+2)^{2}}\textup{d}x\). (Total 6 marks)
▶️Answer/Explanation
Ans
Substituting \(u=x+2\Rightarrow u-2=x,\textup{d}u=\textup{d}x\) (M1)
\(\int \frac{x^{3}}{(x+2)^{2}}\textup{d}x=\frac{(u-2)^{3}}{u^{2}}\textup{d}u\) A1
\(=\int \frac{u^{3}-6u^{2}+12u-8}{u^{2}}\textup{d}u\) A1
\(\int u\, \textup{d}u+\int (-6)\textup{d}u+\int \frac{12}{u}\textup{d}u+\int 8u^{-2}\textup{d}u\) A1
\(=\frac{u^{2}}{2}-6u+12\textup{In}\left | u \right |+8u^{-1}+c\) A1
\(=\frac{(x+2)^{2}}{2}-6(x+2)+12\, \textup{In}\left | x+2 \right |+\frac{8}{x+2}+c\) A1 [6]
Question
Find \(\int \frac{e^{x}}{e^{2x}+9}dx\). (Total 5 marks)
Extra question
Find in a similar way the integral \(\int \frac{3^{x}}{9^{x}+9}dx\)
▶️Answer/Explanation
Ans
\(\textup{Let }u=e^{x}\) M1
\(\textup{d}u=e^{x}\textup{d}x\, (\textup{or equivalent})\) A1
\(\textup{When}\, x=0,u=1\, \textbf{and}\, \textup{when}\, x=\textup{In}\, 3, u=3\) (A1)
\(\int_{0}^{\textup{In}3}\frac{e^{x}}{e^{2x}+9}dx=\int_{1}^{3}\frac{1}{u^{2}+9}\textup{d}u\) A1
\(=\frac{1}{3}\left [ \textup{arctan}\frac{u}{3} \right ]^{3}_{1}\) A1
\(=\frac{1}{3}\left ( \textup{arctan}1-\textup{arctan}\frac{1}{3} \right )\left ( =\frac{\pi }{12}-\frac{1}{3}\textup{arctan}\frac{1}{3},\frac{1}{3}\textup{arctan}\frac{1}{2} \right )\) A1 N0 [6]
Extra question
Find in a similar way the integral \(\int \frac{3^{x}}{9^{x}+9}dx\)
Question
By using an appropriate substitution find \(\int \frac{\textup{tan}(\textup{In}\, y)}{y}dy,y> 0\). (Total 6 marks)
Extra question
The integral \(\int \frac{\textup{cot}(\textup{In}\, y)}{y}dy,y> 0\) can be found in a similar way. Write down the result!
▶️Answer/Explanation
Ans
\(\textup{Let}\, u=\textup{In}\, y\Rightarrow \textup{d}u=\frac{1}{y}\textup{d}y\) A1(A1)
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=\int \textup{tan}\, u\, \textup{d}u\) A1
\(\int \frac{\textup{sin}\, u}{\textup{cos}\, u}\textup{d}u=-\textup{In}\left | \textup{cos}\, u \right |+c\) A1
EITHER
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=-\textup{In}\left | \textup{cos}(\textup{In}\, y) \right |+c\) A1A1
OR
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=\textup{In}\left | \textup{sec}(\textup{In}\, y) \right |+c\) A1A1 [6]
Extra question
\(\textup{In}\left | \textup{sin}(\textup{In}\, y) \right |+c\)
Question
Using the substitution \(2x=\textup{sin}\theta \), or otherwise, find \(\int \left ( \sqrt{1-4x^{2}} \right )dx\). (Total 6 marks)
▶️Answer/Explanation
Ans
\(\int \left (\sqrt{1-4x^{2}} \right )\textup{d}x\)
\(\textup{Let}\, 2x=\textup{sin}\theta \Rightarrow 2\frac{\textup{d}x}{\textup{d}\theta }=\textup{cos}\, \theta \Rightarrow \textup{d}x=\frac{1}{2}\textup{cos}\, \theta \, \textup{d}\, \theta\)
\(\Rightarrow \int \left ( \sqrt{1-4x^{2}} \right )\textup{d}x=\int \sqrt{1-\textup{sin}^{2}\theta \frac{1}{2}}\textup{cos}\,\theta \textup{d}\, \theta \)
\(=\int \frac{1}{2}\textup{cos}^{2}\theta \, \textup{d}\, \theta \) (A1)
\(\int \frac{1}{4}(\textup{cos}\, 2\theta +1)\textup{d}\theta \) (A1)
\(=\frac{1}{8}\textup{sin}\, 2\theta +\frac{\theta }{4}+C\) (A1)(A1)
\(=\frac{1}{4}\left [ 2x\sqrt{1-4x^{2}}+\textup{arcsin}\, 2x \right ]+C\) (A1)(A1) (C6) [6]
Question: [Maximum mark: 21]
The function f is defined by f (x) = ex sinx , where x ∈ R.
(a) Find the Maclaurin series for f (x) up to and including the x3 term.
(b) Hence, find an approximate value for \(\int_{0}^{1}e^{x^{2}} sin(x^{2})dx.\)
The function g is defined by g (x) = ex cos x , where x ∈ R.
(c) (i) Show that g(x) satisfies the equation g ″(x) = 2(g′(x) – g(x)).
(ii) Hence, deduce that g(4) (x) = 2(g″′(x) – g ″(x)) .
(d) Using the result from part (c), find the Maclaurin series for g(x) up to and including the x4 term.
(e) Hence, or otherwise, determine the value of \(\lim_{x\rightarrow 0}\frac{e^{x}cos x – 1 – x}{x^{3}}.\)
▶️Answer/Explanation
Ans:
(a) METHOD 1
recognition of both known series
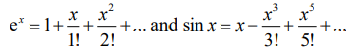
attempt to multiply the two series up to and including x3 term
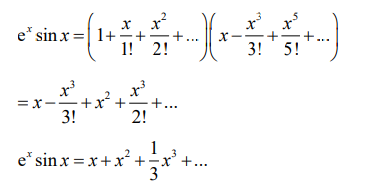
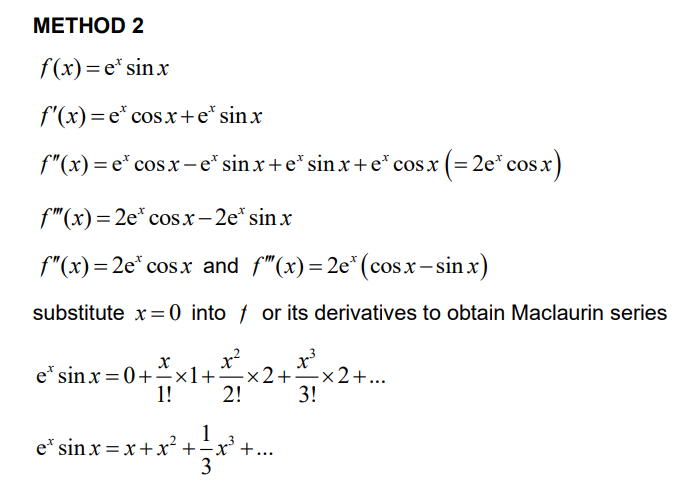
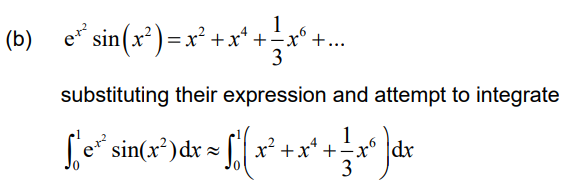
Note: Condone absence of limits up to this stage.
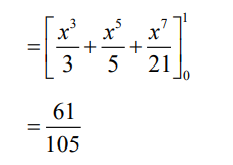
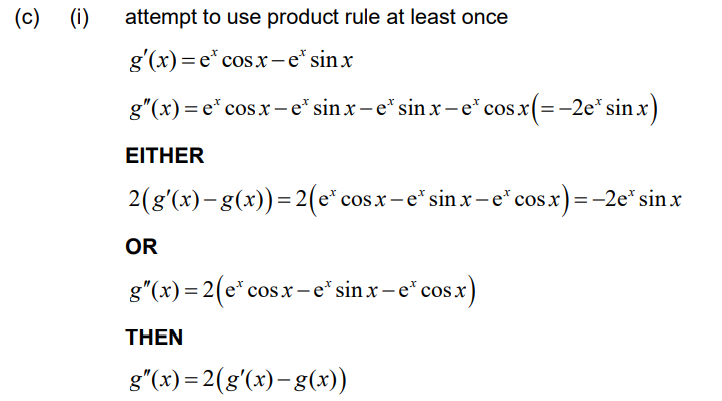
Note: Accept working with each side separately to obtain -2ex sin x .
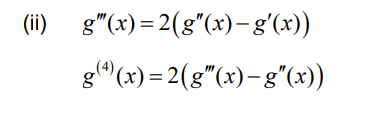
Note: Accept working with each side separately to obtain -4ex cos x .

Note: Do not award any marks for approaches that do not use the part (c) result.
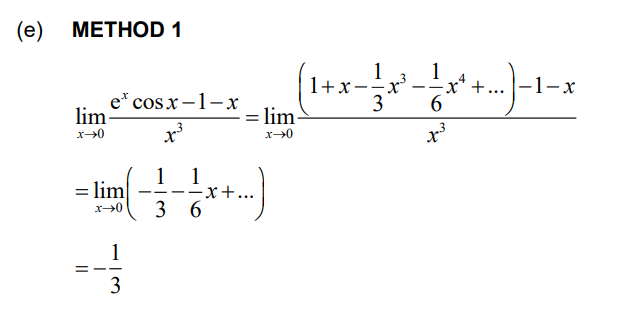
Note: Condone the omission of +… in their working.

Question
By using the substitution x = tan u , find the value of \(\int_0 ^1 \frac{X^2}{(1+X^2)^3}\) [Maximum mark: 8]
▶️Answer/Explanation
Ans:
x= tanu \(\Rightarrow \frac{dx}{du}= sec^{2}u\) OR u= arctan x \(\Rightarrow \frac{du}{dx}\)= \(\frac{1}{1+x^{2}}\)attempt to write the integral in terms of u \(\int_{0}^{\frac{\pi }{4}}\frac{tan^{2}u sec^{2}udu}{(1+tan^{2}u)^{3}} = \int_{0}^{\frac{\pi }{4}}\frac{tan^{2}u sec^{2}udu}{(sec^{2}u)^{3}}= \int_{0}^{\frac{\pi }{4}}sin^{2} u cos^{2}du = \frac{1}{4}\int_{0}^{\frac{\pi }{4}}sin^{2}2udu= \frac{1}{8}\int_{0}^{\frac{\pi }{4}}(1-cos4u)du \)
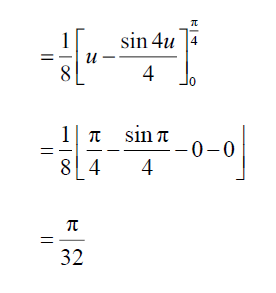
Question
By using the substitution u = sin x , find \(\int \frac{sinx. cosx}{sin^2x-sinx-2}dx \)
▶️Answer/Explanation
Ans:
Let $u=\sin x$, then $\frac{\text{d}u}{\text{d}x}=\cos x$.
$$\begin{eqnarray}
\int\frac{\sin x\cos x}{\sin ^2-\sin x-2} \text{d}x &=& \int\frac{u}{u^2-u-2} \text{d}u \nonumber \\
&=& \int\frac{u}{\left(u-2\right)\left(u+1\right)} \text{d}u \nonumber \\
&=& \frac{1}{3}\int\frac{2}{u-2}+\frac{1}{u+1} \text{d}u \nonumber \\
&=& \frac{1}{3}\left[2\ln\left|u-2\right|+\ln\left|u+1\right|\right]+c \nonumber \\
&=& \frac{1}{3}\left[\ln\left|\left(u-2\right)^2\left(u+1\right)\right|\right]+c \nonumber \\
&=& \frac{1}{3}\left[\ln\left|\left(\sin x-2\right)^2\left(\sin x+1\right)\right|\right]+c.
\end{eqnarray}$$
Question
By using the substitution u = sin x , find \(\int \frac{sinx. cosx}{sin^2x-sinx-2}dx \)
▶️Answer/Explanation
Ans:
Let $u=\sin x$, then $\frac{\text{d}u}{\text{d}x}=\cos x$.
$$\begin{eqnarray}
\int\frac{\sin x\cos x}{\sin ^2-\sin x-2} \text{d}x &=& \int\frac{u}{u^2-u-2} \text{d}u \nonumber \\
&=& \int\frac{u}{\left(u-2\right)\left(u+1\right)} \text{d}u \nonumber \\
&=& \frac{1}{3}\int\frac{2}{u-2}+\frac{1}{u+1} \text{d}u \nonumber \\
&=& \frac{1}{3}\left[2\ln\left|u-2\right|+\ln\left|u+1\right|\right]+c \nonumber \\
&=& \frac{1}{3}\left[\ln\left|\left(u-2\right)^2\left(u+1\right)\right|\right]+c \nonumber \\
&=& \frac{1}{3}\left[\ln\left|\left(\sin x-2\right)^2\left(\sin x+1\right)\right|\right]+c.
\end{eqnarray}$$
Question
Calculate \(\int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{{{\sec }^2}x}}{{\sqrt[3]{{\tan x}}}}{\text{d}}x} \) .[6]
Find \(\int {{{\tan }^3}x{\text{d}}x} \) .[3]
▶️Answer/Explanation
Markscheme
EITHER
let \(u = \tan x;{\text{ d}}u = {\sec ^2}x{\text{d}}x\) (M1)
consideration of change of limits (M1)
\(\int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{{{\sec }^2}x}}{{\sqrt[3]{{\tan x}}}}{\text{d}}x} = \int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{1}{{{u^{\frac{1}{3}}}}}{\text{d}}u} \) (A1)
Note: Do not penalize lack of limits.
\( = \left[ {\frac{{3{u^{\frac{2}{3}}}}}{2}} \right]_1^{\sqrt 3 }\) A1
\( = \frac{{3 \times {{\sqrt 3 }^{\frac{2}{3}}}}}{2} – \frac{3}{2} = \left( {\frac{{3\sqrt[3]{3} – 3}}{2}} \right)\) A1A1 N0
OR
\(\int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{{{\sec }^2}x}}{{\sqrt[3]{{\tan x}}}}{\text{d}}x} = \left[ {\frac{{3{{(\tan x)}^{\frac{2}{3}}}}}{2}} \right]_{\frac{\pi }{4}}^{\frac{\pi }{3}}\) M2A2
\( = \frac{{3 \times {{\sqrt 3 }^{\frac{2}{3}}}}}{2} – \frac{3}{2} = \left( {\frac{{3\sqrt[3]{3} – 3}}{2}} \right)\) A1A1 N0
[6 marks]
\(\int {{{\tan }^3}x{\text{d}}x} = \int {\tan x({{\sec }^2}x – 1){\text{d}}x} \) M1
\( = \int {(\tan x \times {{\sec }^2}x – \tan x){\text{d}}x} \)
\( = \frac{1}{2}{\tan ^2}x – \ln \left| {\sec x} \right| + C\) A1A1
Note: Do not penalize the absence of absolute value or C.
[3 marks]
Question
(a) Given that \(\alpha > 1\), use the substitution \(u = \frac{1}{x}\) to show that
\[\int_1^\alpha {\frac{1}{{1 + {x^2}}}{\text{d}}x = \int_{\frac{1}{\alpha }}^1 {\frac{1}{{1 + {u^2}}}{\text{d}}x} } .\]
(b) Hence show that \(\arctan \alpha + \arctan \frac{1}{\alpha } = \frac{\pi }{2}\).
▶️Answer/Explanation
Markscheme
(a) \(u = \frac{1}{x} \Rightarrow {\text{d}}u = – \frac{1}{{{x^2}}}{\text{d}}x\) M1
\( \Rightarrow {\text{d}}x = – \frac{{{\text{d}}u}}{{{u^2}}}\) A1
\(\int_1^\alpha {\frac{1}{{1 + {x^2}}}{\text{d}}x = – \int_1^{\frac{1}{\alpha }} {\frac{1}{{1 + {{\left( {\frac{1}{u}} \right)}^2}}}\frac{{{\text{d}}u}}{{{u^2}}}} } \) A1M1A1
Note: Award A1 for correct integrand and M1A1 for correct limits.
\( = \int_{\frac{1}{\alpha }}^1 {\frac{1}{{1 + {u^2}}}{\text{d}}u\,\,\,\,\,} \)(upon interchanging the two limits) AG
(b) \(\arctan x_1^\alpha = \arctan u_{\frac{1}{\alpha }}^1\) A1
\(\arctan \alpha – \frac{\pi }{4} = \frac{\pi }{4} – \arctan \frac{1}{\alpha }\) A1
\(\arctan \alpha + \arctan \frac{1}{\alpha } = \frac{\pi }{2}\) AG
[7 marks]
Question
(i) Sketch the graphs of \(y = \sin x\) and \(y = \sin 2x\) , on the same set of axes, for \(0 \leqslant x \leqslant \frac{\pi }{2}\) .
(ii) Find the x-coordinates of the points of intersection of the graphs in the domain \(0 \leqslant x \leqslant \frac{\pi }{2}\) .
(iii) Find the area enclosed by the graphs.[9]
Find the value of \(\int_0^1 {\sqrt {\frac{x}{{4 – x}}} }{{\text{d}}x} \) using the substitution \(x = 4{\sin ^2}\theta \) .[8]
The increasing function f satisfies \(f(0) = 0\) and \(f(a) = b\) , where \(a > 0\) and \(b > 0\) .
(i) By reference to a sketch, show that \(\int_0^a {f(x){\text{d}}x = ab – \int_0^b {{f^{ – 1}}(x){\text{d}}x} } \) .
(ii) Hence find the value of \(\int_0^2 {\arcsin \left( {\frac{x}{4}} \right){\text{d}}x} \) .[8]
▶️Answer/Explanation
Markscheme
(i)
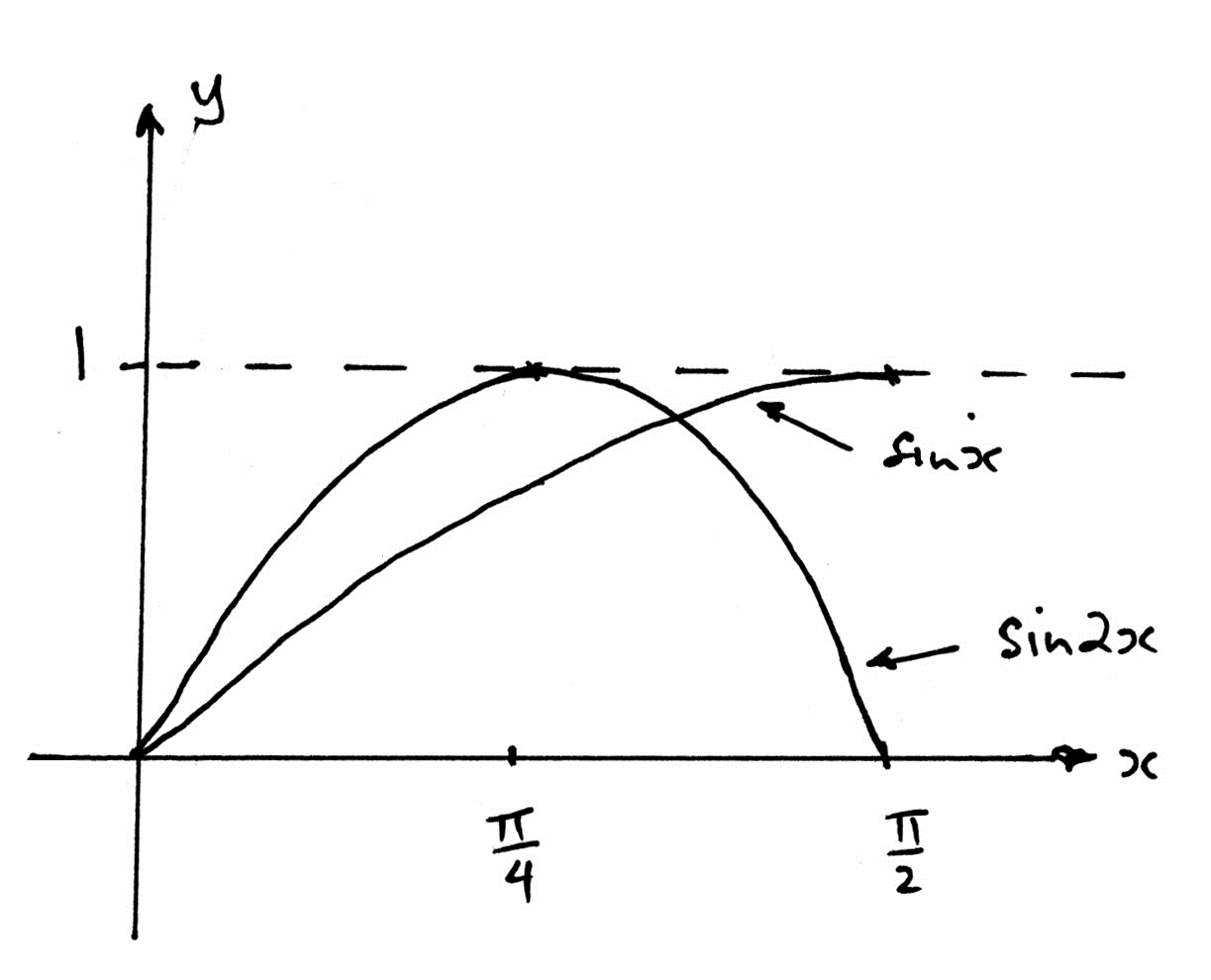 A2
A2
Note: Award A1 for correct \(\sin x\) , A1 for correct \(\sin 2x\) .
Note: Award A1A0 for two correct shapes with \(\frac{\pi }{2}\) and/or 1 missing.
Note: Condone graph outside the domain.
(ii) \(\sin 2x = \sin x\) , \(0 \leqslant x \leqslant \frac{\pi }{2}\)
\(2\sin x\cos x – \sin x = 0\) M1
\(\sin x(2\cos x – 1) = 0\)
\(x = 0,\frac{\pi }{3}\) A1A1 N1N1
(iii) area \( = \int_0^{\frac{\pi }{3}} {(\sin 2x – \sin x){\text{d}}x} \) M1
Note: Award M1 for an integral that contains limits, not necessarily correct, with \(\sin x\) and \(\sin 2x\) subtracted in either order.
\( = \left[ { – \frac{1}{2}\cos 2x + \cos x} \right]_0^{\frac{\pi }{3}}\) A1
\( = \left( { – \frac{1}{2}\cos \frac{{2\pi }}{3} + \cos \frac{\pi }{3}} \right) – \left( { – \frac{1}{2}\cos 0 + \cos 0} \right)\) (M1)
\( = \frac{3}{4} – \frac{1}{2}\)
\( = \frac{1}{4}\) A1
[9 marks]
\(\int_0^1 {\sqrt {\frac{x}{{4 – x}}} } {\text{d}}x = \int_0^{\frac{\pi }{6}} {\sqrt {\frac{{4{{\sin }^2}\theta }}{{4 – 4{{\sin }^2}\theta }}} \times 8\sin \theta \cos \theta {\text{d}}\theta } \) M1A1A1
Note: Award M1 for substitution and reasonable attempt at finding expression for dx in terms of \({\text{d}}\theta \) , first A1 for correct limits, second A1 for correct substitution for dx .
\(\int_0^{\frac{\pi }{6}} {8{{\sin }^2}\theta {\text{d}}\theta } \) A1
\(\int_0^{\frac{\pi }{6}} {4 – 4\cos 2\theta {\text{d}}\theta } \) M1
\( = [4\theta – 2\sin 2\theta ]_0^{\frac{\pi }{6}}\) A1
\( = \left( {\frac{{2\pi }}{3} – 2\sin \frac{\pi }{3}} \right) – 0\) (M1)
\( = \frac{{2\pi }}{3} – \sqrt 3 \) A1
[8 marks]
(i)
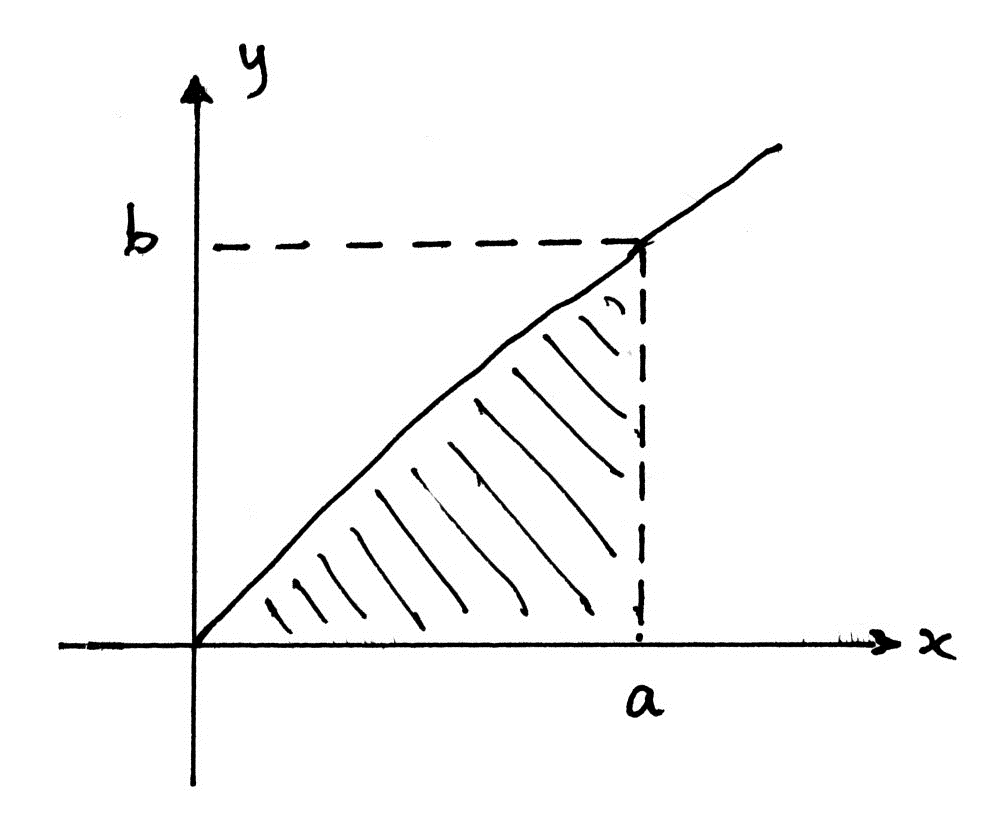 M1
M1
from the diagram above
the shaded area \( = \int_0^a {f(x){\text{d}}x = ab – \int_0^b {{f^{ – 1}}(y){\text{d}}y} } \) R1
\({ = ab – \int_0^b {{f^{ – 1}}(x){\text{d}}x} }\) AG
(ii) \(f(x) = \arcsin \frac{x}{4} \Rightarrow {f^{ – 1}}(x) = 4\sin x\) A1
\(\int_0^2 {\arcsin \left( {\frac{x}{4}} \right){\text{d}}x = \frac{\pi }{3} – \int_0^{\frac{\pi }{6}} {4\sin x{\text{d}}x} } \) M1A1A1
Note: Award A1 for the limit \(\frac{\pi }{6}\) seen anywhere, A1 for all else correct.
\( = \frac{\pi }{3} – [ – 4\cos x]_0^{\frac{\pi }{6}}\) A1
\( = \frac{\pi }{3} – 4 + 2\sqrt 3 \) A1
Note: Award no marks for methods using integration by parts.
[8 marks]
Question
Let \(f(x) = \sqrt {\frac{x}{{1 – x}}} ,{\text{ }}0 < x < 1\).
Show that \(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) and deduce that f is an increasing function.[5]
Show that the curve \(y = f(x)\) has one point of inflexion, and find its coordinates.[6]
Use the substitution \(x = {\sin ^2}\theta \) to show that \(\int {f(x){\text{d}}x} = \arcsin \sqrt x – \sqrt {x – {x^2}} + c\) .[11]
▶️Answer/Explanation
Markscheme
EITHER
derivative of \(\frac{x}{{1 – x}}\) is \(\frac{{(1 – x) – x( – 1)}}{{{{(1 – x)}^2}}}\) M1A1
\(f'(x) = \frac{1}{2}{\left( {\frac{x}{{1 – x}}} \right)^{ – \frac{1}{2}}}\frac{1}{{{{(1 – x)}^2}}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
OR
\(f(x) = \frac{{{x^{\frac{1}{2}}}}}{{{{(1 – x)}^{\frac{1}{2}}}}}\)
\(f'(x) = \frac{{{{(1 – x)}^{\frac{1}{2}}}\left( {\frac{1}{2}{x^{ – \frac{1}{2}}}} \right) – \frac{1}{2}{x^{\frac{1}{2}}}{{(1 – x)}^{ – \frac{1}{2}}}( – 1)}}{{1 – x}}\) M1A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{1}{2}}} + \frac{1}{2}{x^{\frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) A1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}[1 – x + x]\) M1
\( = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\) AG
\(f'(x) > 0\) (for all \(0 < x < 1\)) so the function is increasing R1
[5 marks]
\(f'(x) = \frac{1}{2}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{3}{2}}}\)
\( \Rightarrow f”(x) = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{3}{2}}} + \frac{3}{4}{x^{ – \frac{1}{2}}}{(1 – x)^{ – \frac{5}{2}}}\) M1A1
\( = -\frac{1}{4}{x^{ – \frac{3}{2}}}{(1 – x)^{ – \frac{5}{2}}}[1 – 4x]\)
\(f”(x) = 0 \Rightarrow x = \frac{1}{4}\) M1A1
\(f”(x)\) changes sign at \(x = \frac{1}{4}\) hence there is a point of inflexion R1
\(x = \frac{1}{4} \Rightarrow y = \frac{1}{{\sqrt 3 }}\) A1
the coordinates are \(\left( {\frac{1}{4},\frac{1}{{\sqrt 3 }}} \right)\)
[6 marks]
\(x = {\sin ^2}\theta \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = 2\sin \theta \cos \theta \) M1A1
\(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \int {\sqrt {\frac{{{{\sin }^2}\theta }}{{1 – {{\sin }^2}\theta }}} 2\sin \theta \cos \theta {\text{d}}\theta } } \) M1A1
\( = \int {2{{\sin }^2}\theta {\text{d}}\theta } \) A1
\( = \int {1 – \cos 2\theta } {\text{d}}\theta \) M1A1
\( = \theta – \frac{1}{2}\sin 2\theta + c\) A1
\(\theta = \arcsin \sqrt x \) A1
\(\frac{1}{2}\sin 2\theta = \sin \theta \cos \theta = \sqrt x \sqrt {1 – x} = \sqrt {x – {x^2}} \) M1A1
hence \(\int {\sqrt {\frac{x}{{1 – x}}} {\text{d}}x = \arcsin \sqrt x } – \sqrt {x – {x^2}} + c\) AG
[11 marks]
Question
The function f is defined by \(f(x) = \frac{1}{{4{x^2} – 4x + 5}}\).
Express \(4{x^2} – 4x + 5\) in the form \(a{(x – h)^2} + k\) where a, h, \(k \in \mathbb{Q}\).[2]
The graph of \(y = {x^2}\) is transformed onto the graph of \(y = 4{x^2} – 4x + 5\). Describe a sequence of transformations that does this, making the order of transformations clear.[3]
Sketch the graph of \(y = f(x)\).[2]
Find the range of f.[2]
By using a suitable substitution show that \(\int {f(x){\text{d}}x = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \).[3]
Prove that \(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{\pi }{{16}}} \).[7]
▶️Answer/Explanation
Markscheme
\(4{(x – 0.5)^2} + 4\) A1A1
Note: A1 for two correct parameters, A2 for all three correct.
[2 marks]
translation \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
0
\end{array}} \right)\) (allow “0.5 to the right”) A1
stretch parallel to y-axis, scale factor 4 (allow vertical stretch or similar) A1
translation \(\left( {\begin{array}{*{20}{c}}
0 \\
4
\end{array}} \right)\) (allow “4 up”) A1
Note: All transformations must state magnitude and direction.
Note: First two transformations can be in either order.
It could be a stretch followed by a single translation of \(\left( {\begin{array}{*{20}{c}}
{0.5} \\
4
\end{array}} \right)\). If the vertical translation is before the stretch it is \(\left( {\begin{array}{*{20}{c}}
0 \\
1
\end{array}} \right)\).
[3 marks]
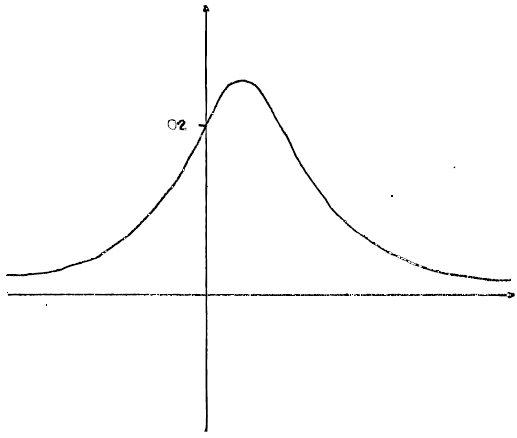
general shape (including asymptote and single maximum in first quadrant), A1
intercept \(\left( {0,\frac{1}{5}} \right)\) or maximum \(\left( {\frac{1}{2},\frac{1}{4}} \right)\) shown A1
[2 marks]
\(0 < f(x) \leqslant \frac{1}{4}\) A1A1
Note: A1 for \( \leqslant \frac{1}{4}\), A1 for \(0 < \).
[2 marks]
let \(u = x – \frac{1}{2}\) A1
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = 1\,\,\,\,\,{\text{(or d}}u = {\text{d}}x)\) A1
\(\int {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \int {\frac{1}{{4{{\left( {x – \frac{1}{2}} \right)}^2} + 4}}{\text{d}}x} } \) A1
\(\int {\frac{1}{{4{u^2} + 4}}{\text{d}}u = \frac{1}{4}\int {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) AG
Note: If following through an incorrect answer to part (a), do not award final A1 mark.
[3 marks]
\(\int_1^{3.5} {\frac{1}{{4{x^2} – 4x + 5}}{\text{d}}x = \frac{1}{4}\int_{0.5}^3 {\frac{1}{{{u^2} + 1}}{\text{d}}u} } \) A1
Note: A1 for correct change of limits. Award also if they do not change limits but go back to x values when substituting the limit (even if there is an error in the integral).
\(\frac{1}{4}\left[ {\arctan (u)} \right]_{0.5}^3\) (M1)
\(\frac{1}{4}\left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) A1
let the integral = I
\(\tan 4I = \tan \left( {\arctan (3) – \arctan \left( {\frac{1}{2}} \right)} \right)\) M1
\(\frac{{3 – 0.5}}{{1 + 3 \times 0.5}} = \frac{{2.5}}{{2.5}} = 1\) (M1)A1
\(4I = \frac{\pi }{4} \Rightarrow I = \frac{\pi }{{16}}\) A1AG
[7 marks]
Question
Use the substitution \(x = a\sec \theta \) to show that \(\int_{a\sqrt 2 }^{2a} {\frac{{{\text{d}}x}}{{{x^3}\sqrt {{x^2} – {a^2}} }} = \frac{1}{{24{a^3}}}\left( {3\sqrt 3 + \pi – 6} \right)} \).
▶️Answer/Explanation
Markscheme
\(x = a\sec \theta \)
\(\frac{{{\text{d}}x}}{{{\text{d}}\theta }} = a\sec \theta \tan \theta \) (A1)
new limits:
\(x = a\sqrt 2 \Rightarrow \theta = \frac{\pi }{4}\) and \(x = 2a \Rightarrow \theta = \frac{\pi }{3}\) (A1)
\(\int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{a\sec \theta \tan \theta }}{{{a^3}{{\sec }^3}\theta \sqrt {{a^2}{{\sec }^2}\theta – {a^2}} }}{\text{d}}\theta } \) M1
\( = \int_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{{{{\cos }^2}\theta }}{{{a^3}}}{\text{d}}\theta } \) A1
using \({\cos ^2}\theta = \frac{1}{2}(\cos 2\theta + 1)\) M1
\(\frac{1}{{2{a^3}}}\left[ {\frac{1}{2}\sin 2\theta + \theta } \right]_{\frac{\pi }{4}}^{\frac{\pi }{3}}\) or equivalent A1
\( = \frac{1}{{4{a^3}}}\left( {\frac{{\sqrt 3 }}{2} + \frac{{2\pi }}{3} – 1 – \frac{\pi }{2}} \right)\) or equivalent A1
\( = \frac{1}{{24{a^3}}}\left( {3\sqrt 3 + \pi – 6} \right)\) AG
[7 marks]
Question
By using the substitution \(u = 1 + \sqrt x \), find \(\int {\frac{{\sqrt x }}{{1 + \sqrt x }}{\text{d}}x} \).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{{2\sqrt x }}\) A1
\({\text{d}}x = 2(u – 1){\text{d}}u\)
Note: Award the A1 for any correct relationship between \({\text{d}}x\) and \({\text{d}}u\).
\(\int {\frac{{\sqrt x }}{{1 + \sqrt x }}{\text{d}}x} = 2\int {\frac{{{{(u – 1)}^2}}}{u}{\text{d}}u} \) (M1)A1
Note: Award the M1 for an attempt at substitution resulting in an integral only involving \(u\) .
\( = 2\int {u – 2 + \frac{1}{u}{\text{d}}u} \) (A1)
\( = {u^2} – 4u + 2\ln u( + C)\) A1
\( = x – 2\sqrt x – 3 + 2\ln \left( {1 + \sqrt x } \right)( + C)\) A1
Note: Award the A1 for a correct expression in \(x\), but not necessarily fully expanded/simplified.
[6 marks]
Question
By using the substitution \(u = {{\text{e}}^x} + 3\), find \(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 6{{\text{e}}^x} + 13}}{\text{d}}x} \).
▶️Answer/Explanation
Markscheme
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = {{\text{e}}^x}\) (A1)
EITHER
integral is \(\int {\frac{{{{\text{e}}^x}}}{{{{({{\text{e}}^x} + 3)}^2} + {2^2}}}{\text{d}}x} \) M1A1
\( = \frac{1}{{{u^2} + {2^2}}}{\text{d}}u\) M1A1
Note: Award M1 only if the integral has completely changed to one in \(u\).
Note: \({\text{d}}u\) needed for final A1
OR
\({{\text{e}}^x} = u – 3\)
integral is \(\int {\frac{1}{{{{(u – 3)}^2} + 6(u – 3) + 13}}{\text{d}}u} \) M1A1
Note: Award M1 only if the integral has completely changed to one in \(u\).
\( = \int {\frac{1}{{{u^2} + {2^2}}}{\text{d}}u} \) M1A1
Note: In both solutions the two method marks are independent.
THEN
\( = \frac{1}{2}\arctan \left( {\frac{u}{2}} \right)( + c)\) (A1)
\( = \frac{1}{2}\arctan \left( {\frac{{{{\text{e}}^x} + 3}}{2}} \right)( + c)\) A1
Total [7 marks]
Question
By using the substitution \(t = \tan x\), find \(\int {\frac{{{\text{d}}x}}{{1 + {{\sin }^2}x}}} \).
Express your answer in the form \(m\arctan (n\tan x) + c\), where \(m\), \(n\) are constants to be determined.
▶️Answer/Explanation
Markscheme
EITHER
\(x = \arctan t\) (M1)
\(\frac{{{\text{d}}x}}{{{\text{d}}t}} = \frac{1}{{1 + {t^2}}}\) A1
OR
\(t = \tan x\)
\(\frac{{{\text{d}}t}}{{{\text{d}}x}} = {\sec ^2}x\) (M1)
\( = 1 + {\tan ^2}x\) A1
\( = 1 + {t^2}\)
THEN
\(\sin x = \frac{t}{{\sqrt {1 + {t^2}} }}\) (A1)
Note: This A1 is independent of the first two marks
\(\int {\frac{{{\text{d}}x}}{{1 + {{\sin }^2}x}} = \int {\frac{{\frac{{{\text{d}}t}}{{1 + {t^2}}}}}{{1 + {{\left( {\frac{t}{{\sqrt {1 + {t^2}} }}} \right)}^2}}}} } \) M1A1
Note: Award M1 for attempting to obtain integral in terms of \(t\) and \({\text{d}}t\)
\( = \int {\frac{{{\text{d}}t}}{{(1 + {t^2}) + {t^2}}} = \int {\frac{{{\text{d}}t}}{{1 + 2{t^2}}}} } \) A1
\( = \frac{1}{2}\int {\frac{{{\text{d}}t}}{{\frac{1}{2} + {t^2}}} = \frac{1}{2} \times \frac{1}{{\frac{1}{{\sqrt 2 }}}}\arctan \left( {\frac{t}{{\frac{1}{{\sqrt 2 }}}}} \right)} \) A1
\( = \frac{{\sqrt 2 }}{2}\arctan \left( {\sqrt 2 \tan x} \right)( + c)\) A1
[8 marks]
Question
Use the substitution \(u = \ln x\) to find the value of \(\int_{\text{e}}^{{{\text{e}}^2}} {\frac{{{\text{d}}x}}{{x\ln x}}} \).
▶️Answer/Explanation
Markscheme
METHOD 1
\(\int_{\text{e}}^{{{\text{e}}^2}} {\frac{{{\text{d}}x}}{{x\ln x}}} = \left[ {\ln (\ln x)} \right]_{\text{e}}^{{{\text{e}}^2}}\) (M1)A1
\( = \ln (\ln {{\text{e}}^2}) – \ln (\ln {\text{e}})\;\;\;( = \ln 2 – \ln 1)\) (A1)
\( = \ln 2\) A1
[4 marks]
METHOD 2
\(u = \ln x,{\text{ }}\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{x}\) M1
\( = \int_1^2 {\frac{{{\text{d}}u}}{u}} \) A1
Note: Condone absent or incorrect limits here.
\( = [\ln u]_1^2\) or equivalent in \(x( = \ln 2 – \ln 1)\) (A1)
\( = \ln 2\) A1
[4 marks]
Question
Consider the function defined by \(f(x) = x\sqrt {1 – {x^2}} \) on the domain \( – 1 \le x \le 1\).
Show that \(f\) is an odd function.[2]
Find \(f'(x)\).[3]
Hence find the \(x\)-coordinates of any local maximum or minimum points.[3]
Find the range of \(f\).[3]
Sketch the graph of \(y = f(x)\) indicating clearly the coordinates of the \(x\)-intercepts and any local maximum or minimum points.[3]
Find the area of the region enclosed by the graph of \(y = f(x)\) and the \(x\)-axis for \(x \ge 0\).[4]
Show that \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \).[2]
▶️Answer/Explanation
Markscheme
\(f( – x) = ( – x)\sqrt {1 – {{( – x)}^2}} \) M1
\( = – x\sqrt {1 – {x^2}} \)
\( = – f(x)\) R1
hence \(f\) is odd AG
[2 marks]
\(f'(x) = x \bullet \frac{1}{2}{(1 – {x^2})^{ – \frac{1}{2}}} \bullet – 2x + {(1 – {x^2})^{\frac{1}{2}}}\) M1A1A1
[3 marks]
\(f'(x) = \sqrt {1 – {x^2}} – \frac{{{x^2}}}{{\sqrt {1 – {x^2}} }}\;\;\;\left( { = \frac{{1 – 2{x^2}}}{{\sqrt {1 – {x^2}} }}} \right)\) A1
Note: This may be seen in part (b).
Note: Do not allow FT from part (b).
\(f'(x) = 0 \Rightarrow 1 – 2{x^2} = 0\) M1
\(x = \pm \frac{1}{{\sqrt 2 }}\) A1
[3 marks]
\(y\)-coordinates of the Max Min Points are \(y = \pm \frac{1}{2}\) M1A1
so range of \(f(x)\) is \(\left[ { – \frac{1}{2},{\text{ }}\frac{1}{2}} \right]\) A1
Note: Allow FT from (c) if values of \(x\), within the domain, are used.
[3 marks]
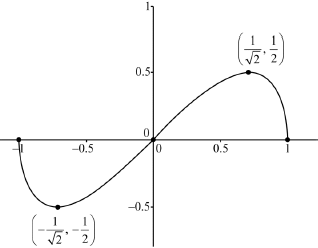
Shape: The graph of an odd function, on the given domain, s-shaped,
where the max(min) is the right(left) of \(0.5{\text{ }}( – 0.5)\) A1
\(x\)-intercepts A1
turning points A1
[3 marks]
\({\text{area}} = \int_0^1 {x\sqrt {1 – {x^2}} {\text{d}}x} \) (M1)
attempt at “backwards chain rule” or substitution M1
\( = – \frac{1}{2}\int_0^1 {( – 2x)\sqrt {1 – {x^2}} {\text{d}}x} \)
Note: Condone absence of limits for first two marks.
\( = \left[ {\frac{2}{3}{{(1 – {x^2})}^{\frac{3}{2}}} \bullet – \frac{1}{2}} \right]_0^1\) A1
\( = \left[ { – \frac{1}{3}{{(1 – {x^2})}^{\frac{3}{2}}}} \right]_0^1\)
\( = 0 – \left( { – \frac{1}{3}} \right) = \frac{1}{3}\) A1
[4 marks]
\(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > 0} \) R1
\(\left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right| = 0\) R1
so \(\int_{ – 1}^1 {\left| {x\sqrt {1 – {x^2}} } \right|{\text{d}}x > \left| {\int_{ – 1}^1 {x\sqrt {1 – {x^2}} {\text{d}}x} } \right|} \) AG
[2 marks]
Total [20 marks]
Question
The following diagram shows the graph of \(y = \frac{{{{(\ln x)}^2}}}{x},{\text{ }}x > 0\).
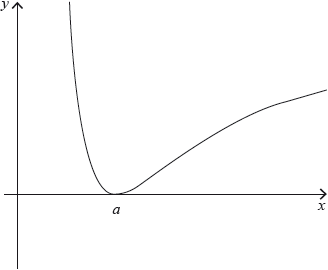
The region \(R\) is enclosed by the curve, the \(x\)-axis and the line \(x = e\).
Let \({I_n} = \int_1^{\text{e}} {\frac{{{{(\ln x)}^n}}}{{{x^2}}}{\text{d}}x,{\text{ }}n \in \mathbb{N}} \).
a.Given that the curve passes through the point \((a,{\text{ }}0)\), state the value of \(a\).[1]
(ii) Prove that \({I_n} = \frac{1}{{\text{e}}} + n{I_{n – 1}},{\text{ }}n \in {\mathbb{Z}^ + }\).
(iii) Hence find the value of \({I_1}\).[7]
▶️Answer/Explanation
Markscheme
\(a = 1\) A1
[1 mark]
\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{x}\) (A1)
\(\int {\frac{{{{(\ln x)}^2}}}{x}{\text{d}}x = \int {{u^2}{\text{d}}u} } \) M1A1
area \( = \left[ {\frac{1}{3}{u^3}} \right]_0^1\) or \(\left[ {\frac{1}{3}{{(\ln x)}^3}} \right]_1^{\text{e}}\) A1
\( = \frac{1}{3}\) A1
[5 marks]
(i) \({I_0} = \left[ { – \frac{1}{x}} \right]_1^{\text{e}}\) (A1)
\( = 1 – \frac{1}{{\text{e}}}\) A1
(ii) use of integration by parts M1
\({I_n} = \left[ { – \frac{1}{x}{{(\ln x)}^n}} \right]_1^{\text{e}} + \int_1^{\text{e}} {\frac{{n{{(\ln x)}^{n – 1}}}}{{{x^2}}}{\text{d}}x} \) A1A1
\( = – \frac{1}{{\text{e}}} + n{I_{n – 1}}\) AG
Note: If the substitution \(u = \ln x\) is used A1A1 can be awarded for \({I_n} = [ – {{\text{e}}^{ – u}}{u^n}]_0^1 + \int_0^1 n {{\text{e}}^{ – u}}{u^{n – 1}}{\text{d}}u\).
(iii) \({I_1} = – \frac{1}{{\text{e}}} + 1 \times {I_0}\) (M1)
\( = 1 – \frac{2}{{\text{e}}}\) A1
[7 marks]
(d) volume \( = \pi \int_1^{\text{e}} {\frac{{{{(\ln x)}^4}}}{{{x^2}}}{\text{d}}x{\text{ }}( = \pi {I_4})} \) (A1)
EITHER
\({I_4} = – \frac{1}{{\text{e}}} + 4{I_3}\) M1A1
\( = – \frac{1}{{\text{e}}} + 4\left( { – \frac{1}{{\text{e}}} + 3{I_2}} \right)\) M1
\( = – \frac{5}{{\text{e}}} + 12{I_2} = – \frac{5}{{\text{e}}} + 12\left( { – \frac{1}{{\text{e}}} + 2{I_1}} \right)\)
OR
using parts \(\int_1^{\text{e}} {\frac{{{{(\ln x)}^4}}}{{{x^2}}}{\text{d}}x = – \frac{1}{{\text{e}}} + 4\int_1^{\text{e}} {\frac{{{{(\ln x)}^3}}}{{{x^2}}}{\text{d}}x} } \) M1A1
\( = – \frac{1}{{\text{e}}} + 4\left( { – \frac{1}{{\text{e}}} + 3\int_1^{\text{e}} {\frac{{{{(\ln x)}^2}}}{{{x^2}}}{\text{d}}x} } \right)\) M1
THEN
\( = – \frac{{17}}{{\text{e}}} + 24\left( {1 – \frac{2}{{\text{e}}}} \right) = 24 – \frac{{65}}{{\text{e}}}\) A1
volume \( = \pi \left( {24 – \frac{{65}}{{\text{e}}}} \right)\)
[5 marks]
Question
a.Using the substitution \(x = \tan \theta \) show that \(\int\limits_0^1 {\frac{1}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{d}}x = } \int\limits_0^{\frac{\pi }{4}} {{{\cos }^2}\theta {\text{d}}\theta } \).[4]
▶️Answer/Explanation
Markscheme
let \(x = \tan \theta \)
\( \Rightarrow \frac{{{\text{d}}x}}{{{\text{d}}\theta }} = {\sec ^2}\theta \) (A1)
\(\int {\frac{1}{{{{({x^2} + 1)}^2}}}{\text{d}}x = \int {\frac{{{{\sec }^2}\theta }}{{{{({{\tan }^2}\theta + 1)}^2}}}{\text{d}}\theta } } \) M1
Note: The method mark is for an attempt to substitute for both \(x\) and \({\text{d}}x\).
\( = \int {\frac{1}{{{{\sec }^2}\theta }}{\text{d}}\theta } \) (or equivalent) A1
when \(x = 0,{\text{ }}\theta = 0\) and when \(x = 1,{\text{ }}\theta = \frac{\pi }{4}\) M1
\(\int\limits_0^{\frac{\pi }{4}} {{{\cos }^2}\theta {\text{d}}\theta } \) AG
[4 marks]
\(\left( {\int\limits_0^1 {\frac{1}{{{{\left( {{x^2} + 1} \right)}^2}}}{\text{d}}x} = \int\limits_0^{\frac{\pi }{4}} {{{\cos }^2}\theta {\text{d}}\theta } } \right) = \frac{1}{2}\int\limits_0^{\frac{\pi }{4}} {\left( {1 + \cos 2\theta } \right){\text{d}}\theta } \) M1
\( = \frac{1}{2}\left[ {\theta + \frac{{\sin 2\theta }}{2}} \right]_0^{\frac{\pi }{4}}\) A1
\( = \frac{\pi }{8} + \frac{1}{4}\) A1
[3 marks]
Question
a.Use the substitution \(u = {x^{\frac{1}{2}}}\) to find \(\int {\frac{{{\text{d}}x}}{{{x^{\frac{3}{2}}} + {x^{\frac{1}{2}}}}}} \).[4]
b.Hence find the value of \(\frac{1}{2}\int\limits_1^9 {\frac{{{\text{d}}x}}{{{x^{\frac{3}{2}}} + {x^{\frac{1}{2}}}}}} \), expressing your answer in the form arctan \(q\), where \(q \in \mathbb{Q}\).[3]
▶️Answer/Explanation
Markscheme
a.\(\frac{{{\text{d}}u}}{{{\text{d}}x}} = \frac{1}{2}{x^{ – \frac{1}{2}}}\) (accept \({\text{d}}u = \frac{1}{2}{x^{ – \frac{1}{2}}}{\text{d}}x\) or equivalent) A1
substitution, leading to an integrand in terms of \(u\) M1
\(\int {\frac{{2u{\text{d}}u}}{{{u^3} + u}}} \) or equivalent A1
= 2 arctan \(\left( {\sqrt x } \right)\left( { + c} \right)\) A1
[4 marks]
\(\frac{1}{2}\int\limits_1^9 {\frac{{{\text{d}}x}}{{{x^{\frac{3}{2}}} + {x^{\frac{1}{2}}}}}} \) = arctan 3 − arctan 1 A1
tan(arctan 3 − arctan 1) = \(\frac{{3 – 1}}{{1 + 3 \times 1}}\) (M1)
tan(arctan 3 − arctan 1) = \(\frac{1}{2}\)
arctan 3 − arctan 1 = arctan \(\frac{1}{2}\) A1
[3 marks]
Question
a.Find the value of the integral \(\int_0^{\sqrt 2 } {\sqrt {4 – {x^2}}f {\text{d}}x} \) .[7]
Find the value of the integral \(\int_0^{0.5} {\arcsin x {\text{d}}x} \) .[5]
Using the substitution \(t = \tan \theta \) , find the value of the integral
\[\int_0^{\frac{\pi }{4}} {\frac{{{\text{d}}\theta }}{{3{{\cos }^2}\theta + {{\sin }^2}\theta }}} {\text{ }}.\][7]
▶️Answer/Explanation
Markscheme
a.let \(x = 2\sin \theta \) M1
\({\text{d}}x = 2\cos \theta {\text{d}}\theta \) A1
\(I = \int_0^{\frac{\pi }{4}} {2\cos \theta \times 2\cos \theta {\text{d}}\theta \,\,\,\,\,\left( { = 4\int_0^{\frac{\pi }{4}} {{{\cos }^2}\theta {\text{d}}\theta } } \right)} \) A1A1
Note: Award A1 for limits and A1 for expression.
\( = 2\int_0^{\frac{\pi }{4}} {(1 + \cos 2\theta ){\text{d}}\theta } \) A1
\( = 2\left[ {\theta + \frac{1}{2}\sin 2\theta } \right]_0^{\frac{\pi }{4}}\) A1
\( = 1 + \frac{\pi }{2}\) A1
[7 marks]
\(I = [x\arcsin x]_0^{0.5} – \int_0^{0.5} {x \times \frac{1}{{\sqrt {1 – {x^2}} }}{\text{d}}x} \) M1A1A1
\( = [x\arcsin x]_0^{0.5} + \left[ {\sqrt {1 – {x^2}} } \right]_0^{0.5}\) A1
\( = \frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} – 1\) A1
[5 marks]
\({\text{d}}t = {\sec ^2}\theta {\text{d}}\theta {\text{ , }}\left[ {0,\frac{\pi }{4}} \right] \to [0,{\text{ 1]}}\) A1(A1)
\(I = \int_0^1 {\frac{{\frac{{{\text{d}}t}}{{(1 + {t^2})}}}}{{\frac{3}{{(1 + {t^2})}} + \frac{{{t^2}}}{{(1 + {t^2})}}}}} \) M1(A1)
\( = \int_0^1 {\frac{{{\text{d}}t}}{{3 + {t^2}}}} \) A1
\( = \frac{1}{{\sqrt 3 }}\left[ {\arctan \left( {\frac{x}{{\sqrt 3 }}} \right)} \right]_0^1\) A1
\( = \frac{\pi }{{6\sqrt 3 }}\) A1
[7 marks]
Question
Find
(a) \(\int (2x+1)^{3}\: dx\) (b) \(\int (2x^{2}+1)^{3}\: dx\) (c) \(\int \frac{(2x^{2}+1)^{3}}{x}dx\)
▶️Answer/Explanation
Ans
(a) \(\int (2x+1)^{3}dx=\frac{(2x+1)^{4}}{8}+c\)
(b) \(\int (2x^{2}+1)^{3}\, dx=\int (8x^{6}+12x^{4}+6x^{2}+1)dx=\frac{8x^{7}}{7}+\frac{12x^{5}}{5}+2x^{3}+x+c\)
(c) \(\int \frac{(2x^{2}+1)^{3}}{x}dx=\int (8x^{5}+12x^{3}+6x+\frac{1}{x})dx=\frac{8x^{6}}{3}+3x^{4}+3x^{2}+\textup{In}\left | x \right |+c\)
Question
Use the double angle identities to calculate
(a) \(\int \textup{cos}^{2}\; xdx\) (b) \(\int \textup{sin}^{2}\; xdx\) (c)\(\int \textup{sin}\, x\, \textup{cos}\, xdx\) (d) \(\int \textup{sin}\, 5x\, \textup{cos}\, 5xdx\)
▶️Answer/Explanation
Ans
(a) \(\int \textup{cos}^{2}\: xdx=\frac{1}{2}\int (1+\textup{cos2}x)dx=\frac{x}{2}+\frac{\textup{sin2}x}{4}+c\)
(b) \(\int \textup{sin}^{2}\: xdx=\frac{1}{2}\int (1-\textup{cos2}x)dx=\frac{x}{2}-\frac{\textup{sin2}x}{4}+c\)
(c) \(\int \textup{sin}\, x\, \textup{cos}\, xdx=\frac{1}{2}\int \textup{sin}\, 2xdx=-\frac{\textup{cos}2x}{4}+c\)
(d) \(\int \textup{sin}\, 5x\, \textup{cos}\, 5xdx=\frac{1}{2}\int \textup{sin}10xdx=-\frac{\textup{cos}10x}{20}+c\)
Questions
Find
(a) \(\int \sqrt{x}(x^{3}-1)dx\) (b) \(\int \frac{3x^{2}-x+2\sqrt{x}}{3\sqrt{x}}dx\)
▶️Answer/Explanation
Ans
(a) \(\int \sqrt{x}(x^{3}-1)dx=\int (x^{3.5}-x^{0.5})dx=\frac{x^{4.5}}{4.5}-\frac{x^{1.5}}{1.5}+c\)
(b) \(\int \frac{3x^{2}-x+2\sqrt{2}}{3\sqrt{x}}dx=\int (x^{1.5}-\frac{1}{3}x^{0.5}+\frac{2}{3})dx=\frac{x^{2.5}}{2.5}-\frac{x^{1.5}}{4.5}+\frac{2}{3}x+c\)
Question
Find (a) \(\int \frac{e^{3x}+2e^{x}+4}{3e^{2x}}dx\) (b) \(\int \frac{8^{x}+2^{x}+1}{4^{x}}dx\).
▶️Answer/Explanation
Ans
(a) \(\int \frac{e^{3x}+2e^{x}+4}{3e^{2x}}dx=\int (\frac{1}{3}e^{x}-\frac{2}{3}e^{-x}+\frac{4}{3}e^{-2x})dx=\frac{1}{3}e^{x}+\frac{2}{3}e^{-x}-\frac{2}{3}e^{-2x}+c\)
(b) \(\int \frac{8^{x}+2^{x}+1}{4^{x}}dx=\int (2^{x}-2^{-x}+4^{-x})dx=\frac{2^{x}}{\textup{In}\, 2}+\frac{2^{-x}}{\textup{In}\, 2}-\frac{4^{-x}}{\textup{In}\, 4}+c\)
Question
Let \({f}'(x)=2e^{-x}+10\, \textup{sin}\, 5x+1\).
Find \(f (x)\) , given that the curve of this function passes through the point A(0,5).
▶️Answer/Explanation
Ans
\(f(x)=-2e^{-x}-2\textup{cos}5x+x+c\)
\(f(0)=5\Leftrightarrow -2-2+0+c=5\Leftrightarrow c=9\)
Hence, \(f(x)=-2e^{-x}-2\textup{cos}5x+x+9\)
Question
Let \({f}”(x)=6ax+b\).
Find \(f (x)\) , given that the function has a maximum at A(1,5) and a point of inflection at B(0,3)
▶️Answer/Explanation
Ans
\({f}”(x)=6ax+b\), \({f}'(x)=3ax^{2}+bx+c\) and \(f(x)=ax^{3}+\frac{b}{2}x^{2}+cx+d\)
| Point of inflection at B(0,3) | \(\Rightarrow {f}”(0)=0\) | and | \(f(0)=3\) |
| \(\Rightarrow b=0\) | and | \(d=3\) | |
| Max at A(1,5) | \(\Rightarrow {f}'(1)=0\) | and | \(f(1)=5\) |
| \(\Rightarrow 3a+c=0\) | and | \(a+c+3=5\) | |
| \(\Rightarrow 3a+c=0\) | and | \(a+c=2\) | |
| \(\Rightarrow a=-1\) | and | \(c=3\) |
Therefore, \(f(x)=-x^{3}+3x+3\)
Question
Find
(a) \(\int \frac{7}{16+x^{2}}dx\) (b) \(\int \frac{7}{1+16x^{2}}dx\) (c) \(\int \frac{7}{25+16x^{2}}dx\) (d) \(\int \frac{7}{2+x^{2}}dx\) (e) \(\int \frac{7}{2+3x^{2}}dx\)
▶️Answer/Explanation
Ans
(a) \(\int \frac{7}{16+x^{2}}dx=\frac{7}{4}\textup{arctan}\frac{x}{4}+c\)
(b) \(\int \frac{7}{1+16x^{2}}dx=\frac{7}{4}\textup{arctan}\, 4x+c\)
(c) \(\int \frac{7}{25+16x^{2}}dx=\frac{7}{20}\textup{arctan}\frac{4x}{5}+c\)
(d) \(\int \frac{7}{2+x^{2}}dx=\frac{7}{\sqrt{2}}\textup{arctan}\frac{x}{\sqrt{2}}+c\)
(e) \(\int \frac{7}{2+3x^{2}}dx=\frac{7}{\sqrt{6}}\textup{arctan}\sqrt{\frac{3}{2}}x+c\)
Question
Find
(a) \(\int \frac{7}{\sqrt{16-x^{2}}}dx\) (b) \(\int \frac{7}{\sqrt{1-16x^{2}}}dx\) (c) \(\int \frac{7}{\sqrt{25-16x^{2}}}dx\) (d) \(\int \frac{7}{\sqrt{2-x^{2}}}dx\) (e) \(\int \frac{7}{\sqrt{2-3x^{2}}}dx\)
▶️Answer/Explanation
Ans
(a) \(\int \frac{7}{\sqrt{16-x^{2}}}dx=7\, \textup{arcsin}\frac{x}{4}+c\)
(b) \(\int \frac{7}{\sqrt{1-16x^{2}}}dx=\frac{7}{4}\, \textup{arcsin}\, 4x+c\)
(c) \(\int \frac{7}{\sqrt{25-16x^{2}}}dx=\frac{7}{4}\, \textup{arcsin}\frac{4x}{5}+c\)
(d) \(\int \frac{7}{\sqrt{2-x^{2}}}dx=7\, \textup{arcsin}\frac{x}{\sqrt{2}}+c\)
(e) \(\int \frac{7}{\sqrt{2-3x^{2}}}dx=\frac{7}{\sqrt{3}}\, \textup{arcsin}\sqrt{\frac{3}{2}}x+c\)
Question
Find (a) \(\int \frac{7}{(x-1)^{2}+4}dx\) (b) \(\int \frac{7}{4(x-1)^{2}+1}dx\)
▶️Answer/Explanation
Ans
(a) \(\int \frac{7}{(x-1)^{2}+4}dx=\frac{7}{2}\textup{arctan}\frac{x-1}{2}+c\) (b) \(\int \frac{7}{4(x-1)^{2}+1}dx=\frac{7}{2}\textup{arctan}(2x-2)+c\)
Question
Find (a) \(\int \frac{7}{\sqrt{4-(x-1)^{2}}}dx\) (b) \(\int \frac{7}{\sqrt{1-4(x-1)^{2}}}dx\)
▶️Answer/Explanation
Ans
(a) \(\int \frac{7}{\sqrt{4-(x-1)^{2}}}dx=7\textup{arcsin}\frac{x-1}{2}+c\) (b) \(\int \frac{7}{\sqrt{1-4(x-1)^{2}}}dx=\frac{7}{2}\textup{arcsin}(2x-2)+c\)
Question
(a) Express \(\frac{2}{x^{2}-10x+24}\) in partial fractions
(b) Express \(x^{2}-10x+26\) in vertex form
(c) Find the integrals
(i) \(\int \frac{2}{x^{2}-10x+24}dx\) (ii) \(\int \frac{2}{x^{2}-10x+25}dx\) (iii) \(\int \frac{2}{x^{2}-10x+26}dx\)
▶️Answer/Explanation
Ans
(a) \(\frac{2}{x^{2}-10x+24}=\frac{A}{x-6}+\frac{B}{x-4}\Rightarrow 2=A(x-4)+B(x-6)\)
For \(x=6,\, 2A=2\Leftrightarrow A=1\)
For \(x=4,\, -2B=2\Leftrightarrow B=-1\)
Hence, \(\frac{2}{x^{2}-10x+24}=\frac{1}{x-6}-\frac{1}{x-4}\)
(b) \(x^{2}-10x+26=(x-5)^{2}+1\)
(c) (i) \(\int \frac{2}{x^{2}-10x+24}dx=\int \frac{1}{x-6}-\frac{1}{x-4}dx=\textup{In}\left | x-6 \right |-\textup{In}\left | x-4 \right |+c=\, \textup{In}\left | \frac{x-6}{x-4} \right |+c\)
(ii) \(\int \frac{2}{x^{2}-10x+25}dx=\int \frac{2}{(x-5)^{2}}dx=-\frac{2}{x-5}+c\)
(iii) \(\int \frac{2}{x^{2}-10x+26}dx=\int \frac{2}{(x-5)^{2}+1}dx=2\, \textup{arctan}(x-5)+c\)
Question
Let \(f(x)=\frac{x^{2}+3x+12}{x(x+2)^{2}}\)
(a) Show that \(f(x)=\frac{3}{x}-\frac{2}{(x+2)}-\frac{5}{(x+2)^{2}}\)
(b) Hence find \(\int f(x)dx\)
▶️Answer/Explanation
Ans
(b) \(\int f(x)dx=3\, \textup{In}\left | x \right |-2\, \textup{In}\left | x+2 \right |+\frac{5}{x+2}+c\)
Question
Complete the following table. [Look at the formula booklet!]
| Integral | Result |
| \(\int \textup{sec}^{2}\, xdx\) | |
| \(\int (\textup{tan}^{2}\, x+1)dx\) | |
| \(\int \frac{5}{\textup{cos}^{2}\, x}dx\) | |
| \(\int \textup{csc}^{2}\, xdx\) | |
| \(\int (\textup{cot}^{2}\, x+1)dx\) | |
| \(\int \frac{5}{\textup{sin}^{2}\, x}dx\) | |
| \(\int \textup{sec}\, x\, \textup{tan}\, xdx\) | |
| \(\int \textup{csc}\, x\, \textup{cot}\, xdx\) | |
| \(\int \textup{tan}^{2}\, xdx\) | |
| \(\int \textup{cot}^{2}\, xdx\) |
▶️Answer/Explanation
Ans
| Integral | Result |
| \(\int \textup{sec}^{2}\, xdx\) | \(\textup{tan}\, x+c\) |
| \(\int (\textup{tan}^{2}\, x+1)dx\) | \(\textup{tan}\, x+c\) |
| \(\int \frac{5}{\textup{cos}^{2}\, x}dx\) | \(5\, \textup{tan}\, x+c\) |
| \(\int \textup{csc}^{2}\, xdx\) | \(-\textup{cot}\, x+c\) |
| \(\int (\textup{cot}^{2}\, x+1)dx\) | \(-\textup{cot}\, x+c\) |
| Integral | Result |
| \(\int \frac{5}{\textup{sin}^{2}\, x}dx\) | \(-5\, \textup{cot}\, x+c\) |
| \(\int \textup{sec}\, x\, \textup{tan}\, xdx\) | \(\textup{sec}\, x+c\) |
| \(\int \textup{csc}\, x\, \textup{cot}\, xdx\) | \(-\, \textup{csc}\, x+c\) |
| \(\int \textup{tan}^{2}\, xdx\) | \(\textup{tan}\, x\, -x+c\) |
| \(\int \textup{cot}^{2}\, xdx\) | \(-\textup{cot}\, x\, -x+c\) |
Question
Let \(f(t)=t^{\frac{1}{3}}\left ( 1-\frac{1}{2t^{\frac{5}{3}}} \right )\). Find \(\int f(t)\, \textup{d}t\). (Total 3 marks)
▶️Answer/Explanation
Ans
\(\int t^{\frac{1}{3}}\left ( 1-\frac{1}{2t^{\frac{2}{5}}} \right )\textup{d}t=\int t^{\frac{1}{3}}\left ( 1-\frac{t^{\frac{5}{3}}}{2} \right )\textup{d}t=\int \left ( t^{\frac{1}{3}}-\frac{t^{\frac{4}{3}}}{2} \right )\textup{d}t\) (M1)
\(=\frac{3}{4}t^{\frac{4}{3}}+\frac{3}{2}t^{\frac{1}{3}}+c\) (M1)(A1) (C3)
Note: Do not penalise for the absence of +C. [3]
Question
The function \({f}’\) is given by \({f}'(x)=2\, \textup{sin}\left ( 5x-\frac{\pi }{2} \right )\).
(a) Write down \({f}”(x)\). (b) Given that \(f\left ( \frac{\pi}{2} \right )=1\), find \(f(x)\).
(Total 6 marks)
▶️Answer/Explanation
Ans
(a) Using the chain rule \({f}'(x)=\left ( 2\, \textup{cos}\left ( 5x-\frac{\pi }{2} \right ) \right )5\) (M1)
\(=10\, \textup{cos}\left ( 5x-\frac{\pi }{2} \right )\) A1 2
(b) \(f(x)=\int {f}'(x)dx=-\frac{2}{5}\textup{cos}\left ( 5x-\frac{\pi }{2} \right )+c\) A1
Substituting to find \(c,f\left ( \frac{\pi }{2} \right )=\frac{2}{5}\textup{cos}\left ( 5\left ( \frac{\pi }{2} \right )-\frac{\pi }{2} \right )+c=1\) M1
\(c=1+\frac{2}{5}\textup{cos}2\pi =1+\frac{2}{5}=\frac{7}{5}\) (A1)
\(f(x)=\frac{2}{5}\textup{cos}\left ( 5x-\frac{\pi }{2} \right )+\frac{7}{5}\) A1 4 [6]
Question
Find the indefinite integrals
(a) \(\int \frac{1}{x^{2}+2}dx\) (b) \(\int \frac{x}{x^{2}+2}dx\) (c) \(\int \frac{x^{2}}{x^{2}+2}dx\) (d) \(\int \frac{x^{3}}{x^{2}+2}dx\)
▶️Answer/Explanation
Ans
(a) \(\frac{1}{\sqrt{2}}\textup{arctan}\frac{x}{\sqrt{2}}+c\) (b) \(\frac{1}{2}\textup{In}(x^{2}+2)+c\) (c) \(x-\frac{2}{\sqrt{2}}\textup{arctan}\frac{x}{\sqrt{2}}+c\) (d) \(\frac{x^{2}}{2}-\textup{In}(x^{2}+2)+c\)
Question
Find the indefinite integral \(\int \frac{12x+10}{3x^{2}+5x+1}dx\)
▶️Answer/Explanation
Ans
\(2\, \textup{In}(3x^{2}+5x+1)+c\)
Question
Find the indefinite integrals (a) \(\int \textup{tan}\, xdx\) (b) \(\int \textup{cot}\, xdx\)
▶️Answer/Explanation
Ans
(a) \(\int \textup{tan}\, xdx=\int \frac{\textup{sin}\, x}{\textup{cos}\, x}dx=-\textup{In}\left | \textup{cos}\, x \right |+c\) (use the substitution \(u=\textup{cos}\, x\))
(b) \(\int \textup{cot}\, xdx=\int \frac{\textup{cos}\, x}{\textup{sin}\, x}dx=\textup{In}\left | \textup{sin}\, x \right |+c\) (use the substitution \(u=\textup{sin}\, x\))
Question
Find the following indefinite integrals by using the substitution \(u=x^{2}+5\)
(a) \(\int \frac{x^{5}}{x^{2}+5}dx\) (b) \(\int \frac{x^{3}}{\sqrt{x^{2}+5}}dx\) (c) \(\int x^{3}(x^{2}+5)^{5}dx\)
▶️Answer/Explanation
Ans
(a) \(\frac{25}{2}\textup{In}(x^{2}+5)+\frac{(x^{2}+5)^{2}}{4}-5x^{2}+c\) (b) \(\frac{(x^{2}-10)\sqrt{x^{2}+5}}{3}+c\) (c) \(\frac{(x^{2}+5)^{6}(6x^{2}-5)}{84}+c\)
Question
Find the indefinite integrals
(a) \(\int \frac{x}{x^{2}+9}dx\) (b) \(\int \frac{x}{(x^{2}+9)^{2}}dx\) (c) \(\int \frac{x^{2}+x+12}{x^{2}+9}dx\)
▶️Answer/Explanation
Ans(a) \(\frac{1}{2}\textup{In}(x^{2}+9)+c\) (b) \(-\frac{1}{2(x^{2}+9)}+c\) (c) \(\frac{1}{2}\textup{In}(x^{2}+9)+x+\textup{arctan}\frac{x}{3}+c\)
Question
Find the indefinite integrals
(a) \(\int \textup{tan}^{5}\, x\, \textup{sec}^{2}\, xdx\) (b) \(\int \frac{\textup{sec}^{2}\, x}{\sqrt{\textup{tan}\, x}}dx\) (c) \(\int \frac{\textup{sec}^{2}\, x}{e^{\textup{tan}\, x}}dx\) (d) \(\int \frac{\textup{sin}^{5}\, x}{\textup{cos}^{7}\, x}dx\)
▶️Answer/Explanation
Ans
(a) \(\frac{\textup{tan}^{6}\, x}{6}+c\) (b) \(2\sqrt{\textup{tan}\, x}+c\) (c) \(-\frac{1}{e^{\textup{tan}\, x}}+c\) (d) \(\frac{\textup{tan}^{6}\, x}{6}+c\)
Question
(a) Calculate \(\int \frac{1}{5+x^{2}}dx\) , by using the substitution \(x=\sqrt{5}\, \textup{tan}\, \theta \)
(b) Calculate (i) \(\int \frac{1}{\sqrt{5-x^{2}}}dx\) , (ii) \(\int \sqrt{5-x^{2}\, dx}\) by using the substitution \(x=\sqrt{5}\, \textup{sin}\, \theta \)
▶️Answer/Explanation
Ans
(a) \(\frac{1}{\sqrt{5}}\textup{arctan}\frac{x}{\sqrt{5}}+c\) (b) (i) \(\textup{arcsin}\frac{x}{\sqrt{5}}+c\) , (ii) \(\frac{5}{2}\textup{arcsin}\frac{x}{\sqrt{5}}+\frac{x\sqrt{5-x^{2}}}{2}+c\)
Question
Calculate \(\int \sqrt{\frac{x}{4-x}}dx\) , by using the substitution \(x=4\, \textup{sin}^{2}\, \theta \)
Express your answer in the form \(A\, \textup{arcsin}\frac{\sqrt{x}}{2}+B\sqrt{4x-x^{2}}+c\)
▶️Answer/Explanation
Ans
\(4\, \textup{arcsin}\frac{\sqrt{x}}{2}-\sqrt{4x-x^{2}}+c\)
Question
(a) Show that \(\frac{2x+4}{(x^{2}+4)(x-2)}=\frac{1}{x-2}-\frac{x}{x^{2}+4}\)
(b) Hence find \(\int \frac{2x+4}{(x^{2}+4)(x-2)}dx\)
▶️Answer/Explanation
Ans
(b) \(\textup{In}(x-2)-\frac{1}{2}\textup{In}(x^{2}+4)+c\)
Question
Using the substitution \(y=2-x\), or otherwise, find \(\int \left ( \frac{x}{2-x} \right )^{2}dx\). (Total 6 marks)
▶️Answer/Explanation
Ans
\(I=\int \left ( \frac{2-y}{y} \right )^{2}(-dy)\) (M1)(A1)
\(=\int \left ( \frac{4}{y^{2}}-\frac{4}{y}+1 \right )\textup{d}y=\frac{4}{y}+4\, \textup{In}\left | y \right |-y+c\) (A1)(A1)(A1)
\(=\frac{4}{2-x}+4\textup{In}\left | 2-x \right |-(2-x)+c\) (A1) (C6)
Note: c and modulus signs not required. [6]
Question
Using the substitution \(u=\frac{1}{2}x+1\),or otherwise, find the integral \(\int x\sqrt{\frac{1}{2}x+1}\: dx\). (Total 4 marks)
▶️Answer/Explanation
Ans
Let \(u=\frac{1}{2}x+1\Leftrightarrow x=2(u-1)\Rightarrow \frac{\textup{d}x}{\textup{d}u}=2\)
Then \(\int x\left ( \frac{1}{2}x+1 \right )^{1/2}dx\)
\(=\int 2(u-1)\times u^{1/2}\times 2\textup{d}u\) (M1)
\(=4\int (u^{3/2}-u^{1/2})\textup{d}u\) (A1)
\(=4\left [ \frac{2}{5}u^{5/2}-\frac{2}{3}u^{3/2} \right ]+C\) (M1)
\(=4\left [ \frac{2}{5}\left ( \frac{1}{2}x+1 \right )^{5/2}-\frac{2}{3}\left ( \frac{1}{2}x+1 \right )^{3/2} \right ]+C\) (A1) [4]
Question
Use the substitution \(u=x+2\) to find \(\int \frac{x^{3}}{(x+2)^{2}}\textup{d}x\). (Total 6 marks)
▶️Answer/Explanation
Ans
Substituting \(u=x+2\Rightarrow u-2=x,\textup{d}u=\textup{d}x\) (M1)
\(\int \frac{x^{3}}{(x+2)^{2}}\textup{d}x=\frac{(u-2)^{3}}{u^{2}}\textup{d}u\) A1
\(=\int \frac{u^{3}-6u^{2}+12u-8}{u^{2}}\textup{d}u\) A1
\(\int u\, \textup{d}u+\int (-6)\textup{d}u+\int \frac{12}{u}\textup{d}u+\int 8u^{-2}\textup{d}u\) A1
\(=\frac{u^{2}}{2}-6u+12\textup{In}\left | u \right |+8u^{-1}+c\) A1
\(=\frac{(x+2)^{2}}{2}-6(x+2)+12\, \textup{In}\left | x+2 \right |+\frac{8}{x+2}+c\) A1 [6]
Question
Find \(\int \frac{e^{x}}{e^{2x}+9}dx\). (Total 5 marks)
Extra question
Find in a similar way the integral \(\int \frac{3^{x}}{9^{x}+9}dx\)
▶️Answer/Explanation
Ans
\(\textup{Let }u=e^{x}\) M1
\(\textup{d}u=e^{x}\textup{d}x\, (\textup{or equivalent})\) A1
\(\textup{When}\, x=0,u=1\, \textbf{and}\, \textup{when}\, x=\textup{In}\, 3, u=3\) (A1)
\(\int_{0}^{\textup{In}3}\frac{e^{x}}{e^{2x}+9}dx=\int_{1}^{3}\frac{1}{u^{2}+9}\textup{d}u\) A1
\(=\frac{1}{3}\left [ \textup{arctan}\frac{u}{3} \right ]^{3}_{1}\) A1
\(=\frac{1}{3}\left ( \textup{arctan}1-\textup{arctan}\frac{1}{3} \right )\left ( =\frac{\pi }{12}-\frac{1}{3}\textup{arctan}\frac{1}{3},\frac{1}{3}\textup{arctan}\frac{1}{2} \right )\) A1 N0 [6]
Extra question
Find in a similar way the integral \(\int \frac{3^{x}}{9^{x}+9}dx\)
Question
By using an appropriate substitution find \(\int \frac{\textup{tan}(\textup{In}\, y)}{y}dy,y> 0\). (Total 6 marks)
Extra question
The integral \(\int \frac{\textup{cot}(\textup{In}\, y)}{y}dy,y> 0\) can be found in a similar way. Write down the result!
▶️Answer/Explanation
Ans
\(\textup{Let}\, u=\textup{In}\, y\Rightarrow \textup{d}u=\frac{1}{y}\textup{d}y\) A1(A1)
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=\int \textup{tan}\, u\, \textup{d}u\) A1
\(\int \frac{\textup{sin}\, u}{\textup{cos}\, u}\textup{d}u=-\textup{In}\left | \textup{cos}\, u \right |+c\) A1
EITHER
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=-\textup{In}\left | \textup{cos}(\textup{In}\, y) \right |+c\) A1A1
OR
\(\int \frac{\textup{tan}(\textup{In}\, y)}{y}\textup{d}y=\textup{In}\left | \textup{sec}(\textup{In}\, y) \right |+c\) A1A1 [6]Extra question
\(\textup{In}\left | \textup{sin}(\textup{In}\, y) \right |+c\)
Question
Using the substitution \(2x=\textup{sin}\theta \), or otherwise, find \(\int \left ( \sqrt{1-4x^{2}} \right )dx\). (Total 6 marks)
▶️Answer/Explanation
Ans
\(\int \left (\sqrt{1-4x^{2}} \right )\textup{d}x\)
\(\textup{Let}\, 2x=\textup{sin}\theta \Rightarrow 2\frac{\textup{d}x}{\textup{d}\theta }=\textup{cos}\, \theta \Rightarrow \textup{d}x=\frac{1}{2}\textup{cos}\, \theta \, \textup{d}\, \theta\)
\(\Rightarrow \int \left ( \sqrt{1-4x^{2}} \right )\textup{d}x=\int \sqrt{1-\textup{sin}^{2}\theta \frac{1}{2}}\textup{cos}\,\theta \textup{d}\, \theta \)
\(=\int \frac{1}{2}\textup{cos}^{2}\theta \, \textup{d}\, \theta \) (A1)
\(\int \frac{1}{4}(\textup{cos}\, 2\theta +1)\textup{d}\theta \) (A1)
\(=\frac{1}{8}\textup{sin}\, 2\theta +\frac{\theta }{4}+C\) (A1)(A1)
\(=\frac{1}{4}\left [ 2x\sqrt{1-4x^{2}}+\textup{arcsin}\, 2x \right ]+C\) (A1)(A1) (C6) [6]