Question
The random variable X has the negative binomial distribution NB(5, p), where p < 0.5, and \({\text{P}}(X = 10) = 0.05\). By first finding the value of p, find the value of \({\text{P}}(X = 11)\).
▶️Answer/Explanation
Markscheme
\({\text{P}}(X = 10) = \left( {\begin{array}{*{20}{c}}
9 \\
4
\end{array}} \right){p^5}{(1 – p)^5}\) (= 0.05) (M1)A1A1
Note: First A1 is for the binomial coefficient. Second A1 is for the rest.
solving by any method, \(p = 0.297 \ldots \) A4
Notes: Award A2 for anything which rounds to 0.703.
Do not apply any AP at this stage.
\({\text{P}}(X = 10) = \left( {\begin{array}{*{20}{c}}
{10} \\
4
\end{array}} \right) \times {(0.297…)^5} \times {(1 – 0.297…)^6}\) (M1)A1
= 0.0586 A1
Note: Allow follow through for incorrect p-values.
[10 marks]
Examiners report
Questions on these discrete distributions have not been generally well answered in the past and it was pleasing to note that many candidates submitted a reasonably good solution to this question. In (b), the determination of the value of p was often successful using a variety of methods including solving the equation \(p(1 – p) = {(0.000396{\text{ }} \ldots )^{1/5}}\), graph plotting or using SOLVER on the GDC or even expanding the equation into a \({10^{{\text{th}}}}\) degree polynomial and solving that. Solutions to this particular question exceeded expectations.
Question
As soon as Sarah misses a total of 4 lessons at her school an email is sent to her parents. The probability that she misses any particular lesson is constant with a value of \(\frac{1}{3}\). Her decision to attend a lesson is independent of her previous decisions.
(a) Find the probability that an email is sent to Sarah’s parents after the \({8^{{\text{th}}}}\) lesson that Sarah was scheduled to attend.
(b) If an email is sent to Sarah’s parents after the \({X^{{\text{th}}}}\) lesson that she was scheduled to attend, find \({\text{E}}(X)\).
(c) If after 6 of Sarah’s scheduled lessons we are told that she has missed exactly 2 lessons, find the probability that an email is sent to her parents after a total of 12 scheduled lessons.
(d) If we know that an email was sent to Sarah’s parents immediately after her \({6^{{\text{th}}}}\) scheduled lesson, find the probability that Sarah missed her \({2^{{\text{nd}}}}\) scheduled lesson.
▶️Answer/Explanation
Markscheme
(a) we are dealing with the Negative Binomial distribution: \({\text{NB}}\left( {4,\frac{1}{3}} \right)\) (M1)
let X be the number of scheduled lessons before the email is sent
\({\text{P}}(X = 8) = \left( {\begin{array}{*{20}{c}}
7 \\
3
\end{array}} \right){\left( {\frac{2}{3}} \right)^4}{\left( {\frac{1}{3}} \right)^4} = 0.0854\) (M1)A1
[3 marks]
(b) \({\text{E}}(X) = \frac{r}{p} = \frac{4}{{\frac{1}{3}}} = 12\) (M1)A1
[2 marks]
(c) we are asking for 2 missed lessons in the second 6 lessons, with the last lesson missed so this is \({\text{NB}}\left( {2,\frac{1}{3}} \right)\) (M1)
\({\text{P}}(X = 6) = \left( {\begin{array}{*{20}{c}}
5 \\
1
\end{array}} \right){\left( {\frac{2}{3}} \right)^4}{\left( {\frac{1}{3}} \right)^2} = 0.110\) (M1)A1
Note: Accept solutions laid out in terms of conditional probabilities.
[3 marks]
(d) EITHER
We know that she missed the \({6^{{\text{th}}}}\) lesson so she must have missed 3 from the first 5 lessons. All are equally likely so the probability that she missed the \({2^{{\text{nd}}}}\) lesson is \(\frac{3}{5}\). R1A1
OR
require \({\text{P(missed }}{{\text{2}}^{{\text{nd}}}}|X = 6) = \frac{{{\text{P(missed }}{{\text{2}}^{{\text{nd}}}}{\text{ and }}X = 6)}}{{{\text{P}}(X = 6)}}\) R1
\({\text{P(missed }}{{\text{2}}^{{\text{nd}}}}{\text{ and }}X = 6) = {\text{P(missed }}{{\text{2}}^{{\text{nd}}}}{\text{ and }}{{\text{6}}^{{\text{th}}}}{\text{ and 2 of remaining 4)}}\)
\[ = \frac{1}{3} \cdot \frac{1}{3} \cdot \left( {\begin{array}{*{20}{c}}
4 \\
2
\end{array}} \right){\left( {\frac{1}{3}} \right)^2}{\left( {\frac{2}{3}} \right)^2} = \frac{{24}}{{{3^6}}}\]
\({\text{P}}(X = 6) = \left( {\begin{array}{*{20}{c}}
5 \\
3
\end{array}} \right){\left( {\frac{1}{3}} \right)^4}{\left( {\frac{2}{3}} \right)^2} = \frac{{40}}{{{3^6}}}\)
so required probability is \(\frac{{24}}{{{3^6}}} \cdot \frac{{{3^6}}}{{40}} = \frac{3}{5}\) A1
[2 marks]
Total [10 marks]
Examiners report
Realising that this was a problem about the Negative Binomial distribution was the crucial thing to realise in this question. All parts of the syllabus do need to be covered.
Question
The continuous random variable \(X\) has probability density function
\[f(x) = \left\{ {\begin{array}{*{20}{c}} {{{\text{e}}^{ – x}}}&{x \geqslant 0} \\ 0&{x < 0} \end{array}.} \right.\]
The discrete random variable \(Y\) is defined as the integer part of \(X\), that is the largest integer less than or equal to \(X\).
a.Show that the probability distribution of \(Y\) is given by \({\text{P}}(Y = y) = {{\text{e}}^{ – y}}(1 – {{\text{e}}^{ – 1}}),{\text{ }}y \in \mathbb{N}\).[4]
b.(i) Show that \(G(t)\), the probability generating function of \(Y\), is given by \(G(t) = \frac{{1 – {{\text{e}}^{ – 1}}}}{{1 – {{\text{e}}^{ – 1}}t}}\).
(ii) Hence determine the value of \({\text{E}}(Y)\) correct to three significant figures.[8]
▶️Answer/Explanation
Markscheme
\({\text{P}}(Y = y) = \int_y^{y + 1} {{{\text{e}}^{ – x}}{\text{d}}x} \) M1A1
\( = {[ – {{\text{e}}^{ – x}}]^{y + 1}}y\) A1
\( = – {{\text{e}}^{ – (y + 1)}} + {{\text{e}}^{ – y}}\) A1
\( = {{\text{e}}^{ – y}}(1 – {{\text{e}}^{ – 1}})\) AG
[4 marks]
(i) attempt to use \(G(t) = \sum {{\text{P}}(Y = y){t^y}} \) (M1)
\( = \sum\limits_{y = 0}^\infty {{{\text{e}}^{ – y}}(1 – {{\text{e}}^{ – 1}}){t^y}} \) A1
Note: Accept a listing of terms without the use of \(\Sigma \).
this is an infinite geometric series with first term \(1 – {{\text{e}}^{ – 1}}\) and common ratio \({{\text{e}}^{ – 1}}t\) M1
\(G(t) = \frac{{1 – {{\text{e}}^{ – 1}}}}{{1 – {{\text{e}}^{ – 1}}t}}\) AG
(ii) \({\text{E}}(Y) = G'(1)\) M1
\(G'(t) = \frac{{1 – {{\text{e}}^{ – 1}}}}{{{{(1 – {{\text{e}}^{ – 1}}t)}^2}}} \times {{\text{e}}^{ – 1}}\) (M1)(A1)
\({\text{E}}(Y) = \frac{{{{\text{e}}^{ – 1}}}}{{(1 – {{\text{e}}^{ – 1}})}}\) (A1)
\( = 0.582\) A1
Note: Allow the use of GDC to determine \(G'(1)\).
[8 marks]
Question
Two independent discrete random variables \(X\) and \(Y\) have probability generating functions \(G(t)\) and \(H(t)\) respectively. Let \(Z = X + Y\) have probability generating function \(J(t)\).
a.Write down an expression for \(J(t)\) in terms of \(G(t)\) and \(H(t)\).[1]
b.By differentiating \(J(t)\), prove that
(i) \({\text{E}}(Z) = {\text{E}}(X) + {\text{E}}(Y)\);
(ii) \({\text{Var}}(Z) = {\text{Var}}(X) + {\text{Var}}(Y)\).[10]
▶️Answer/Explanation
Markscheme
\(J(t) = G(t)H(t)\) A1
[1 mark]
(i) \(J'(t) = G'(t)H(t) + G(t)H'(t)\) M1A1
\(J'(1) = G'(1)H(1) + G(1)H'(1)\) M1
\(J'(1) = G'(1) + H'(1)\) A1
so \(E(Z) = E(X) + E(Y)\) AG
(ii) \(J”(t) = G”(t)H(t) + G'(t)H'(t) + G'(t)H'(t) + G(t)H”(t)\) M1A1
\(J”(1) = G”(1)H(1) + 2G'(1)H'(1) + G(1)H”(1)\)
\( = G”(1) + 2G'(1)H'(1) + H”(1)\) A1
\({\text{Var}}(Z) = J”(1) + J'(1) – {\left( {J'(1)} \right)^2}\) M1
\( = G”(1) + 2G'(1)H'(1) + H”(1) + G'(1) + H'(1) – {\left( {G'(1) + H'(1)} \right)^2}\) A1
\( = G”(1) + G'(1) – {\left( {G'(1)} \right)^2} + H”(1) + H'(1) – {\left( {H'(1)} \right)^2}\) A1
so \({\text{Var}}(Z) = {\text{Var}}(X) + {\text{Var}}(Y)\) AG
Note: If addition is wrongly used instead of multiplication in (a) it is inappropriate to give FT apart from the second M marks in each part, as the working is too simple.
[10 marks]
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]
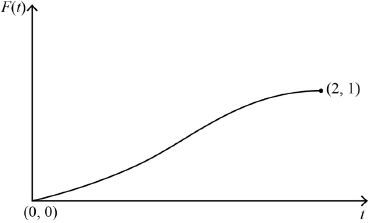
correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]

correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]

correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
A continuous random variable \(T\) has a probability density function defined by
\(f(t) = \left\{ {\begin{array}{*{20}{c}} {\frac{{t(4 – {t^2})}}{4}}&{0 \leqslant t \leqslant 2} \\ {0,}&{{\text{otherwise}}} \end{array}} \right.\).
a.Find the cumulative distribution function \(F(t)\), for \(0 \leqslant t \leqslant 2\).[3]
b.i.Sketch the graph of \(F(t)\) for \(0 \leqslant t \leqslant 2\), clearly indicating the coordinates of the endpoints.[2]
b.ii.Given that \(P(T < a) = 0.75\), find the value of \(a\).[2]
▶️Answer/Explanation
Markscheme
\(F(t) = \int_0^t {\left( {x – \frac{{{x^3}}}{4}} \right){\text{d}}x{\text{ }}\left( { = \int_0^t {\frac{{x(4 – {x^2})}}{4}{\text{d}}x} } \right)} \) M1
\( = \left[ {\frac{{{x^2}}}{2} – \frac{{{x^4}}}{{16}}} \right]_0^t{\text{ }}\left( { = \left[ {\frac{{{x^2}(8 – {x^2})}}{{16}}} \right]_0^t} \right){\text{ }}\left( { = \left[ {\frac{{ – 4 – {x^2}{)^2}}}{{16}}} \right]_0^t} \right)\) A1
\( = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}{\text{ }}\left( { = \frac{{{t^2}(8 – {t^2})}}{{16}}} \right){\text{ }}\left( { = 1 – \frac{{{{(4 – {t^2})}^2}}}{{16}}} \right)\) A1
Note: Condone integration involving \(t\) only.
Note: Award M1A0A0 for integration without limits eg, \(\int {\frac{{t(4 – {t^2})}}{4}{\text{d}}t = \frac{{{t^2}}}{2} – \frac{{{t^4}}}{{16}}} \) or equivalent.
Note: But allow integration \( + \) \(C\) then showing \(C = 0\) or even integration without \(C\) if \(F(0) = 0\) or \(F(2) = 1\) is confirmed.
[3 marks]

correct shape including correct concavity A1
clearly indicating starts at origin and ends at \((2,{\text{ }}1)\) A1
Note: Condone the absence of \((0,{\text{ }}0)\).
Note: Accept 2 on the \(x\)-axis and 1 on the \(y\)-axis correctly placed.
[2 marks]
attempt to solve \(\frac{{{a^2}}}{2} – \frac{{{a^4}}}{{16}} = 0.75\) (or equivalent) for \(a\) (M1)
\(a = 1.41{\text{ }}( = \sqrt 2 )\) A1
Note: Accept any answer that rounds to 1.4.
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
Question
Consider an unbiased tetrahedral (four-sided) die with faces labelled 1, 2, 3 and 4 respectively.
The random variable X represents the number of throws required to obtain a 1.
a.State the distribution of X.[1]
b.Show that the probability generating function, \(G\left( t \right)\), for X is given by \(G\left( t \right) = \frac{t}{{4 – 3t}}\).[4]
c.Find \(G’\left( t \right)\).[2]
d.Determine the mean number of throws required to obtain a 1.[1]
▶️Answer/Explanation
Markscheme
X is geometric (or negative binomial) A1
[1 mark]
\(G\left( t \right) = \frac{1}{4}t + \frac{1}{4}\left( {\frac{3}{4}} \right){t^2} + \frac{1}{4}{\left( {\frac{3}{4}} \right)^2}{t^3} + \ldots \) M1A1
recognition of GP \(\left( {{u_1} = \frac{1}{4}t,\,\,r = \frac{3}{4}t} \right)\) (M1)
\( = \frac{{\frac{1}{4}t}}{{1 – \frac{3}{4}t}}\) A1
leading to \(G\left( t \right) = \frac{t}{{4 – 3t}}\) AG
[4 marks]
attempt to use product or quotient rule M1
\(G’\left( t \right) = \frac{4}{{{{\left( {4 – 3t} \right)}^2}}}\) A1
[2 marks]
4 A1
Note: Award A1FT to a candidate that correctly calculates the value of \(G’\left( 1 \right)\) from their \(G’\left( t \right)\).
[1 mark]
Question
Consider an unbiased tetrahedral (four-sided) die with faces labelled 1, 2, 3 and 4 respectively.
The random variable X represents the number of throws required to obtain a 1.
a.State the distribution of X.[1]
b.Show that the probability generating function, \(G\left( t \right)\), for X is given by \(G\left( t \right) = \frac{t}{{4 – 3t}}\).[4]
c.Find \(G’\left( t \right)\).[2]
d.Determine the mean number of throws required to obtain a 1.[1]
▶️Answer/Explanation
Markscheme
X is geometric (or negative binomial) A1
[1 mark]
\(G\left( t \right) = \frac{1}{4}t + \frac{1}{4}\left( {\frac{3}{4}} \right){t^2} + \frac{1}{4}{\left( {\frac{3}{4}} \right)^2}{t^3} + \ldots \) M1A1
recognition of GP \(\left( {{u_1} = \frac{1}{4}t,\,\,r = \frac{3}{4}t} \right)\) (M1)
\( = \frac{{\frac{1}{4}t}}{{1 – \frac{3}{4}t}}\) A1
leading to \(G\left( t \right) = \frac{t}{{4 – 3t}}\) AG
[4 marks]
attempt to use product or quotient rule M1
\(G’\left( t \right) = \frac{4}{{{{\left( {4 – 3t} \right)}^2}}}\) A1
[2 marks]
4 A1
Note: Award A1FT to a candidate that correctly calculates the value of \(G’\left( 1 \right)\) from their \(G’\left( t \right)\).
[1 mark]