Question
Topic: Uncertainties and errors
Given: A student is verifying the equation
$$
x=\frac{2 \lambda Y}{Z}
$$
The percentage uncertainties are:
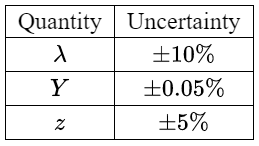
Calculate: the percentage uncertainty in $x$ ?
A. $5 \%$
B. $15 \%$
C. $25 \%$
D. $30 \%$
▶️Answer/Explanation
Ans:B
Solution:
From Formula Booklet:
If: $y=\frac{a b}{c}$ then: $\frac{\Delta y}{y}=\frac{\Delta a}{a}+\frac{\Delta b}{b}+\frac{\Delta c}{c}$
So,
$\frac{\Delta x}{x}=\frac{\Delta \lambda }{\lambda }+\frac{\Delta Y}{Y}+\frac{\Delta Z}{Z}$
Hence percentage uncertainty in $x=10+5+0.05=15 \%$
Question
Topic: Measurements
Given: A student models the relationship between the pressure $p$ of a gas and its temperature $T$ as $p=x+y T$ The units of $p$ are pascal and the units of $T$ are kelvin.
Discuss: the fundamental SI units of $x$ and $y ?$

▶️Answer/Explanation
Ans:A
Solution:
The unit of $x$ can be found by analyzing the given relationship: $p=x+yT$. Since $p$ has units of pascal and $T$ has units of kelvin, the units of $x$ must be such that it cancels out the units of $T$ and leaves behind the units of $p$. Therefore, the units of $x$ are kg m$^{-1}$ s$^{-2}$, which is equivalent to pascal (Pa).
The unit of $y$ can be found by rearranging the given relationship: $p=x+yT \Rightarrow y = \frac{p}{T}$. The units of $y$ can be obtained by dividing the units of $p$ (kg m$^{-1}$ s$^{-2}$) by the units of $T$ (K). This gives units of kg m$^{-1}$ s$^{-2}$ K$^{-1}$, which is equivalent to pascal per kelvin (Pa/K).
Question
Topic: Motion
Given: A sky diver is falling at terminal speed when she opens her parachute.
Discuss: are the direction of her velocity vector and the direction of her acceleration vector before she reaches the new terminal speed?
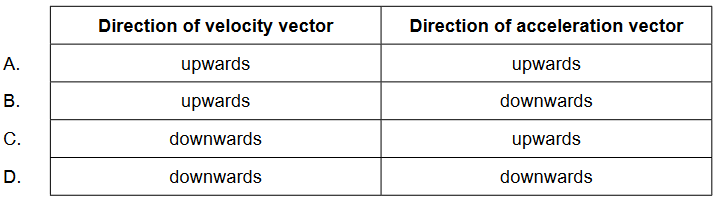
▶️Answer/Explanation
Ans: C
Solution:
The answer is C, downwards for the direction of velocity vector and upwards for the direction of acceleration vector.
When a sky diver is falling at terminal speed, the upward drag force acting on the diver balances the downward force of gravity, resulting in zero net force and a constant velocity. When the diver opens the parachute, the surface area increases and the drag force increases, while the weight of the diver remains the same. This results in a net upward force and an upward acceleration.
Initially, before reaching the new terminal speed, the diver will be falling downwards with a constant velocity. At this point, the direction of the velocity vector is downwards, as this is the direction in which the diver is moving. However, the net force acting on the diver is upwards (due to the drag force being greater than the weight of the diver), and so the direction of the acceleration vector is upwards.
Therefore, the correct answer is downwards for the direction of velocity vector and upwards for the direction of acceleration vector.
Question
Topic: Motion:
Given: A sports car is accelerated from 0 to $100 \mathrm{~km}$ per hour in $3 \mathrm{~s}$.
Calculate: the acceleration of the car?
A. $0.1 \mathrm{~g}$
B. $0.3 \mathrm{~g}$
C. $0.9 \mathrm{~g}$
D. $3 \mathrm{~g}$
▶️Answer/Explanation
Ans:C
Solution:
To solve this problem, we need to convert the initial and final velocities to SI units (meters per second) and use the formula for acceleration:
$$
a=\frac{\Delta v}{\Delta t}
$$
where $\Delta v$ is the change in velocity and $\Delta t$ is the time interval over which the change occurs.
Converting $0\ \mathrm{km/h}$ to meters per second:
$$
0\ \mathrm{km/h}=\frac{0}{3600}\ \mathrm{m/s}=0\ \mathrm{m/s}
$$
Converting $100\ \mathrm{km/h}$ to meters per second:
$$
100\ \mathrm{km/h}=\frac{100\times 1000}{3600}\ \mathrm{m/s}=\frac{250}{9}\ \mathrm{m/s}
$$
Substituting the values into the formula for acceleration:
$$
a=\frac{\Delta v}{\Delta t}=\frac{\frac{250}{9}-0}{3}\ \mathrm{m/s^2}=\frac{250}{27}\ \mathrm{m/s^2}=9.26\ \mathrm{m/s^2}
$$
Now we can compare the calculated acceleration to the given answer choices:
A. $0.1\ \mathrm{g}=\frac{0.1\times 9.81}{1}\ \mathrm{m/s^2}=0.981\ \mathrm{m/s^2}$
B. $0.3\ \mathrm{g}=\frac{0.3\times 9.81}{1}\ \mathrm{m/s^2}=2.943\ \mathrm{m/s^2}$
C. $0.9\ \mathrm{g}=\frac{0.9\times 9.81}{1}\ \mathrm{m/s^2}=8.829\ \mathrm{m/s^2}$
D. $3\ \mathrm{g}=\frac{3\times 9.81}{1}\ \mathrm{m/s^2}=29.43\ \mathrm{m/s^2}$
The calculated acceleration of $9.26\ \mathrm{m/s^2}$ is closest to option C, $0.9\ \mathrm{g}$. Therefore, the answer is (C) $0.9\ \mathrm{g}$.
Question
Topic: Motion
Given: A girl throws an object horizontally at time $t=0$. Air resistance can be ignored. At $t=0.50 \mathrm{~s}$ the object travels horizontally a distance $x$ in metres while it falls vertically through a distance $y$ in metres.
Calculate: is the initial velocity of the object and the vertical distance fallen at $t=1.0 \mathrm{~s} ?$
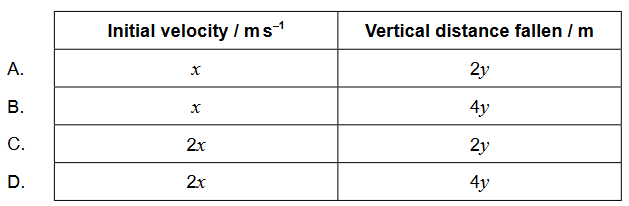
▶️Answer/Explanation
Ans:D
Solution:
From the given information, we can use the kinematic equations to determine the initial velocity and the vertical distance fallen.
First, we can use the horizontal distance formula to find the initial horizontal velocity:
$$
x = v_{0x} t \quad \Rightarrow \quad v_{0x} = \frac{x}{t} = \frac{x}{0.50 \mathrm{~s}} = 2x \mathrm{~s^{-1}}
$$
Since there is no horizontal acceleration, the horizontal velocity remains constant at $v_{0x}$.
Now, we can use the vertical motion equation $y = v_{0y} t + \frac{1}{2}at^2$ to find the initial vertical velocity $v_{0y}$. Since the object is thrown horizontally, the initial vertical velocity is zero, so we can simplify the equation to
$y = \frac{1}{2}at^2$.
At $t = 0.5$ s, the object has fallen a distance $y$ vertically, so we have $y = \frac{1}{2}at^2$, which we can solve for $a$:
$a = \frac{2y}{t^2} = \frac{2 \times y}{0.5^2} = 8 \mathrm{y}$
Now we can use this acceleration to find the vertical distance fallen at $t = 1.0$ s:
$y’ = v_{0y} t + \frac{1}{2}at^2 = \frac{1}{2}at^2 = \frac{1}{2} \times 8 \mathrm{y} \times 1^2 = 4 \mathrm{y}$
Therefore, the vertical distance fallen at $t = 1.0$ s is $4 \mathrm{y}$.
