Multiple Choice Questions
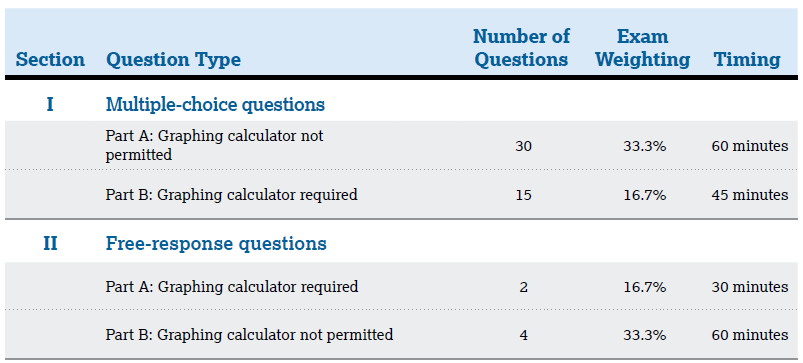
MCQs
- Time: 90 minutes
- 60 multiple – choice questions (core)
- No marks deducted from incorrect answers
- A four-function, scientific, or graphing calculator is allowed
- 50% weight
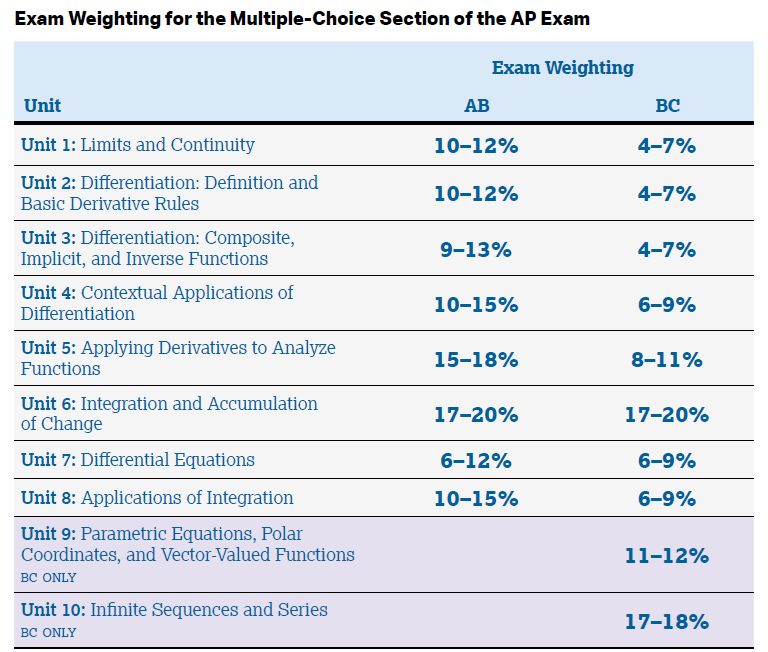
Unit 1: Limits and Continuity
- 1.1 Introducing Calculus: Can Change Occur at an Instant?
- 1.2 Defining Limits and Using Limit Notation
- 1.3 Estimating Limit Values from Graphs
- 1.4 Estimating Limit Values from Tables
- 1.5 Determining Limits Using Algebraic Properties of Limits
- 1.6 Determining Limits Using Algebraic Manipulation
- 1.7 Selecting Procedures for Determining Limits
- 1.8 Determining Limits Using the Squeeze Theorem
- 1.9 Connecting Multiple Representations of Limits
- 1.10 Exploring Types of 3 Discontinuities
- 1.11 Defining Continuity at a Point
- 1.12 Confirming Continuity over an Interval
- 1.13 Removing Discontinuities
- 1.14 Connecting Infinite Limits and Vertical Asymptotes
- 1.15 Connecting Limits at Infinity and Horizontal Asymptotes
- 1.16 Working with the Intermediate Value Theorem (IVT)
Unit 2: Differentiation: Definition and Basic Derivative Rules
- 2.1 Defining Average and Instantaneous Rates of Change at a Point
- 2.2 Defining the Derivative of a Function and Using Derivative Notation
- 2.3 Estimating Derivatives of a Function at a Point
- 2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
- 2.5 Applying the Power Rule
- 2.6 Derivative Rules: Constant, Sum, Difference, and Constant Multiple
- 2.7 Derivatives of cos x, sin x, ex, and ln x
- 2.8 The Product Rule
- 2.9 The Quotient Rule
- 2.10 Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
Unit 4: Contextual Applications of Differentiation
- 4.1 Interpreting the Meaning of the Derivative in Context
- 4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration
- 4.3 Rates of Change in Applied Contexts Other Than Motion
- 4.4 Introduction to Related Rates
- 4.5 Solving Related Rates Problems
- 4.6 Approximating Values of a Function Using Local Linearity and Linearization
- 4.7 Using L’Hospital’s Rule for Determining Limits of Indeterminate Forms
Unit 5: Analytical Applications of Differentiation
- 5.1 Using the Mean Value Theorem
- 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points
- 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing
- 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
- 5.5 Using the Candidates Test to Determine Absolute (Global) Extrema
- 5.6 Determining Concavity of Functions over Their Domains
- 5.7 Using the Second Derivative Test to Determine Extrema
- 5.8 Sketching Graphs of Functions and Their Derivatives
- 5.9 Connecting a Function, Its First Derivative, and Its Second Derivative
- 5.10 Introduction to Optimization Problems
- 5.11 Solving Optimization Problems
- 5.12 Exploring Behaviors of Implicit Relations
Unit 6: Integration and Accumulation of Change
- 6.1 Exploring Accumulations of Change
- 6.2 Approximating Areas with Riemann Sums
- 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
- 6.4 The Fundamental Theorem of Calculus and Accumulation Functions
- 6.5 Interpreting the Behavior of Accumulation Functions Involving Area
- 6.6 Applying Properties of Definite Integrals
- 6.7 The Fundamental Theorem of Calculus and Definite Integrals
- 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
- 6.9 Integrating Using Substitution
- 6.10 Integrating Functions Using Long Division and Completing the Square
- 6.11 Integrating Using Integration by Parts bc only
- 6.12 Using Linear Partial Fractions bc only
- 6.13 Evaluating Improper Integrals bc only
- 6.14 Selecting Techniques for Antidifferentiation
Unit 7: Differential Equations
- 7.1 Modeling Situations with Differential Equations
- 7.2 Verifying Solutions for Differential Equations
- 7.3 Sketching Slope Fields
- 7.4 Reasoning Using Slope Fields
- 7.5 Approximating Solutions Using Euler’s Method bc only
- 7.6 Finding General Solutions Using Separation of Variables
- 7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
- 7.8 Exponential Models with Differential Equations
- 7.9 Logistic Models with Differential Equations bc only
Unit 8: Applications of Integration
- 8.1 Finding the Average Value of a Function on an Interval
- 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
- 8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
- 8.4 Finding the Area Between Curves Expressed as Functions of x
- 8.5 Finding the Area Between Curves Expressed as Functions of y
- 8.6 Finding the Area Between Curves That Intersect at More Than Two Points
- 8.7 Volumes with Cross Sections: Squares and Rectangles
- 8.8 Volumes with Cross Sections: Triangles and Semicircles
- 8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
- 8.10 Volume with Disc Method: Revolving Around Other Axes
- 8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
- 8.12 Volume with Washer Method: Revolving Around Other Axes
- 8.13 The Arc Length of a Smooth, Planar Curve and Distance Traveled bc only
Unit 9: Parametric Equations, Polar Coordinates, and Vector-Valued Functions bc only
- 9.1 Defining and Differentiating Parametric Equations
- 9.2 Second Derivatives of Parametric Equations
- 9.3 Finding Arc Lengths of Curves Given by Parametric Equations
- 9.4 Defining and Differentiating Vector- Valued Functions
- 9.5 Integrating Vector- Valued Functions
- 9.6 Solving Motion Problems Using Parametric and Vector- Valued Functions
- 9.7 Defining Polar Coordinates and Differentiating in Polar Form
- 9.8 Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve
- 9.9 Finding the Area of the Region Bounded by Two Polar Curves
Unit 10 : Infinite Sequences and Series bc only
- 10.1 Defining Convergent and Divergent Infinite Series
- 10.2 Working with Geometric Series
- 10.3 The nth Term Test for Divergence
- 10.4 Integral Test for Convergence
- 10.5 Harmonic Series and p-Series
- 10.6 Comparison Tests for Convergence
- 10.7 Alternating Series Test for Convergence
- 10.8 Ratio Test for Convergence
- 10.9 Determining Absolute or Conditional Convergence
- 10.10 Alternating Series Error Bound
- 10.11 Finding Taylor Polynomial Approximations of Functions
- 10.12 Lagrange Error Bound
- 10.13 Radius and Interval of Convergence of Power Series
- 10.14 Finding Taylor or Maclaurin Series for a Function
- 10.15 Representing Functions as Power Series
Free-Response Questions(FRQs)
Free-Response Questions
- Time: 105 minutes
- 4 Questions
- No marks deducted from incorrect answers
- A four-function, scientific, or graphing calculator is allowed
- 50% weight
Unit 1: Limits and Continuity
- 1.1 Introducing Calculus: Can Change Occur at an Instant?
- 1.2 Defining Limits and Using Limit Notation
- 1.3 Estimating Limit Values from Graphs
- 1.4 Estimating Limit Values from Tables
- 1.5 Determining Limits Using Algebraic Properties of Limits
- 1.6 Determining Limits Using Algebraic Manipulation
- 1.7 Selecting Procedures for Determining Limits
- 1.8 Determining Limits Using the Squeeze Theorem
- 1.9 Connecting Multiple Representations of Limits
- 1.10 Exploring Types of 3 Discontinuities
- 1.11 Defining Continuity at a Point
- 1.12 Confirming Continuity over an Interval
- 1.13 Removing Discontinuities
- 1.14 Connecting Infinite Limits and Vertical Asymptotes
- 1.15 Connecting Limits at Infinity and Horizontal Asymptotes
- 1.16 Working with the Intermediate Value Theorem (IVT)
Unit 2: Differentiation: Definition and Basic Derivative Rules
- 2.1 Defining Average and Instantaneous Rates of Change at a Point
- 2.2 Defining the Derivative of a Function and Using Derivative Notation
- 2.3 Estimating Derivatives of a Function at a Point
- 2.4 Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
- 2.5 Applying the Power Rule
- 2.6 Derivative Rules: Constant, Sum, Difference, and Constant Multiple
- 2.7 Derivatives of cos x, sin x, ex, and ln x
- 2.8 The Product Rule
- 2.9 The Quotient Rule
- 2.10 Finding the Derivatives of Tangent, Cotangent, Secant, and/or Cosecant Functions
Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
Unit 4: Contextual Applications of Differentiation
- 4.1 Interpreting the Meaning of the Derivative in Context
- 4.2 Straight-Line Motion: Connecting Position, Velocity, and Acceleration
- 4.3 Rates of Change in Applied Contexts Other Than Motion
- 4.4 Introduction to Related Rates
- 4.5 Solving Related Rates Problems
- 4.6 Approximating Values of a Function Using Local Linearity and Linearization
- 4.7 Using L’Hospital’s Rule for Determining Limits of Indeterminate Forms
Unit 5: Analytical Applications of Differentiation
- 5.1 Using the Mean Value Theorem
- 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points
- 5.3 Determining Intervals on Which a Function Is Increasing or Decreasing
- 5.4 Using the First Derivative Test to Determine Relative (Local) Extrema
- 5.5 Using the Candidates Test to Determine Absolute (Global) Extrema
- 5.6 Determining Concavity of Functions over Their Domains
- 5.7 Using the Second Derivative Test to Determine Extrema
- 5.8 Sketching Graphs of Functions and Their Derivatives
- 5.9 Connecting a Function, Its First Derivative, and Its Second Derivative
- 5.10 Introduction to Optimization Problems
- 5.11 Solving Optimization Problems
- 5.12 Exploring Behaviors of Implicit Relations
Unit 6: Integration and Accumulation of Change
- 6.1 Exploring Accumulations of Change
- 6.2 Approximating Areas with Riemann Sums
- 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
- 6.4 The Fundamental Theorem of Calculus and Accumulation Functions
- 6.5 Interpreting the Behavior of Accumulation Functions Involving Area
- 6.6 Applying Properties of Definite Integrals
- 6.7 The Fundamental Theorem of Calculus and Definite Integrals
- 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
- 6.9 Integrating Using Substitution
- 6.10 Integrating Functions Using Long Division and Completing the Square
- 6.11 Integrating Using Integration by Parts bc only
- 6.12 Using Linear Partial Fractions bc only
- 6.13 Evaluating Improper Integrals bc only
- 6.14 Selecting Techniques for Antidifferentiation
Unit 7: Differential Equations
- 7.1 Modeling Situations with Differential Equations
- 7.2 Verifying Solutions for Differential Equations
- 7.3 Sketching Slope Fields
- 7.4 Reasoning Using Slope Fields
- 7.5 Approximating Solutions Using Euler’s Method bc only
- 7.6 Finding General Solutions Using Separation of Variables
- 7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
- 7.8 Exponential Models with Differential Equations
- 7.9 Logistic Models with Differential Equations bc only
Unit 8: Applications of Integration
- 8.1 Finding the Average Value of a Function on an Interval
- 8.2 Connecting Position, Velocity, and Acceleration of Functions Using Integrals
- 8.3 Using Accumulation Functions and Definite Integrals in Applied Contexts
- 8.4 Finding the Area Between Curves Expressed as Functions of x
- 8.5 Finding the Area Between Curves Expressed as Functions of y
- 8.6 Finding the Area Between Curves That Intersect at More Than Two Points
- 8.7 Volumes with Cross Sections: Squares and Rectangles
- 8.8 Volumes with Cross Sections: Triangles and Semicircles
- 8.9 Volume with Disc Method: Revolving Around the x- or y-Axis
- 8.10 Volume with Disc Method: Revolving Around Other Axes
- 8.11 Volume with Washer Method: Revolving Around the x- or y-Axis
- 8.12 Volume with Washer Method: Revolving Around Other Axes
- 8.13 The Arc Length of a Smooth, Planar Curve and Distance Traveled bc only
Unit 9: Parametric Equations, Polar Coordinates, and Vector-Valued Functions bc only
- 9.1 Defining and Differentiating Parametric Equations
- 9.2 Second Derivatives of Parametric Equations
- 9.3 Finding Arc Lengths of Curves Given by Parametric Equations
- 9.4 Defining and Differentiating Vector- Valued Functions
- 9.5 Integrating Vector- Valued Functions
- 9.6 Solving Motion Problems Using Parametric and Vector- Valued Functions
- 9.7 Defining Polar Coordinates and Differentiating in Polar Form
- 9.8 Find the Area of a Polar Region or the Area Bounded by a Single Polar Curve
- 9.9 Finding the Area of the Region Bounded by Two Polar Curves
Unit 10 : Infinite Sequences and Series bc only
- 10.1 Defining Convergent and Divergent Infinite Series
- 10.2 Working with Geometric Series
- 10.3 The nth Term Test for Divergence
- 10.4 Integral Test for Convergence
- 10.5 Harmonic Series and p-Series
- 10.6 Comparison Tests for Convergence
- 10.7 Alternating Series Test for Convergence
- 10.8 Ratio Test for Convergence
- 10.9 Determining Absolute or Conditional Convergence
- 10.10 Alternating Series Error Bound
- 10.11 Finding Taylor Polynomial Approximations of Functions
- 10.12 Lagrange Error Bound
- 10.13 Radius and Interval of Convergence of Power Series
- 10.14 Finding Taylor or Maclaurin Series for a Function
- 10.15 Representing Functions as Power Series
Course Content
The AP Chemistry Exam assesses student understanding of the science practices and learning objectives outlined in the course framework. The exam is 3 hours and 15 minutes long and includes 60 multiple-choice questions and 7 free-response questions. Starting with the 2022–23 school year (spring 2023 exam), a scientific or graphing calculator is recommended for use on both sections of the exam. Students are provided with the periodic table and a formula sheet that lists specific and relevant formulas for use on the exam