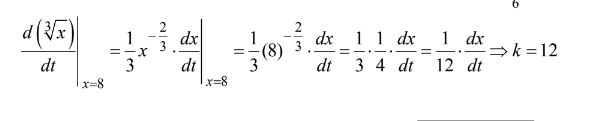Question
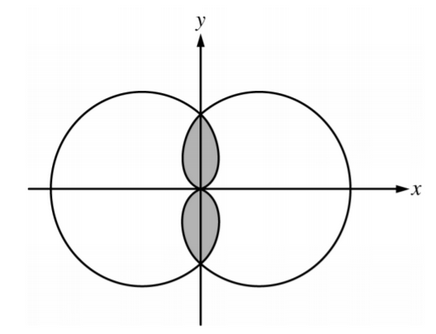
The polar curves \(r= 1 − cosθ\) and \(r=1 + cosθ\) are shown in the figure above. Which of the following expressions gives the total area of the shaded regions?
A \(\int^{π}_{0}(1+cosθ)^2dθ\)
B \(\int^{π}_{π/2}(1+cosθ)^2dθ\)
C \(2\int^{π}_{0}(1-cosθ)^2dθ\)
D \(2\int^{π}_{0}((1−cosθ)^2+(1+cosθ)^2)dθ\)
Answer/Explanation
Question
The area of the region inside the polar curve r = 4sin θ and outside the polar curve r = 2 is given by
(A)\(\frac{1}{2}\int_{0}^{\pi}(4sin\Theta -2)^2d\Theta\)
(B)\(\frac{1}{2}\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}(4sin\Theta -2)^2d\Theta\)
(C)\(\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}(4sin\Theta -2)^2d\Theta\)
(D)\(\frac{1}{2}\int_{\frac{\pi}{6}}^{\frac{5\pi}{6}}(16sin^2\Theta -4)d\Theta\)
(E)\(\frac{1}{2}\int_{0}^{\pi} (16sin^2\Theta -4)d\Theta\)
Answer/Explanation
Ans:D