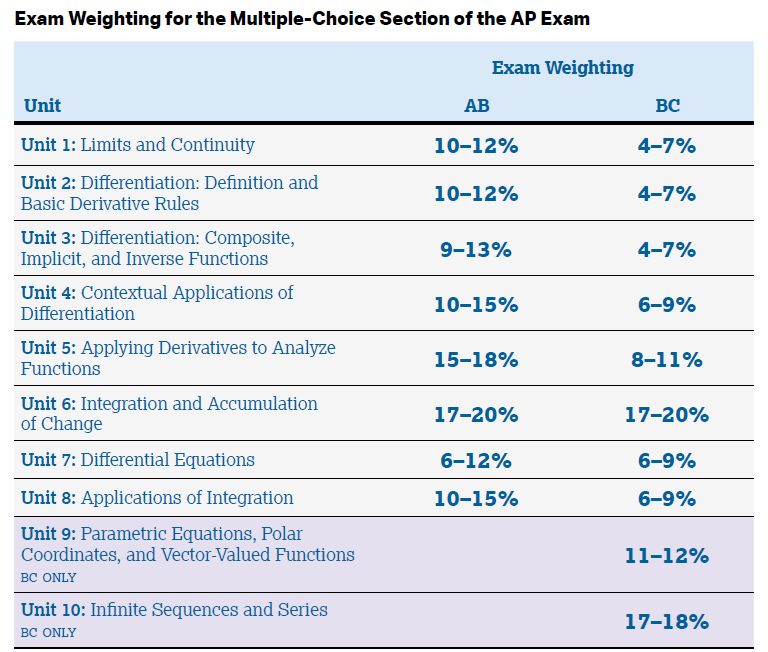
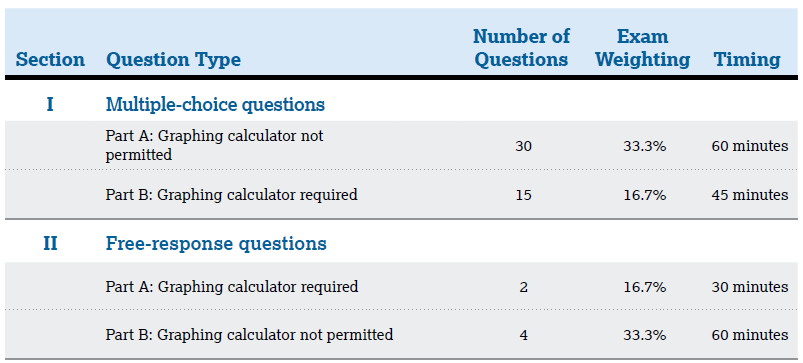
Chapter 2: Differentiation
- 2.1 Definition of Derivatives and the Power Rule
- 2.2 The Product and Quotient Rules and Higher Derivatives
- 2.3 The Chain Rule and the Composite Functions
- 2.4 Derivatives of Trigonometric Functions
- 2.5 Derivatives of Exponential and Logarithmic Functions
- 2.6 The Tangent Lines and the Normal Lines
- 2.7 Implicit Differentiation
- 2.8 Derivatives of an Inverse Function
- 2.9 Derivatives of Inverse Trigonometric Functions
- 2.10 Approximating a Derivative
Chapter 3: Applications of Differentiation
- 3.1 Related Rates
- 3.2 Position, Velocity, and Acceleration
- 3.3 The Roll’s Theorem and The Mean Value Theorem
- 3.4 The First Derivative Test and the Extreme Values of Functions
- 3.5 The Second Derivative Test
- 3.6 Curves of f , f ′, f ′′ and Curve Sketching
- 3.7 Optimization Problems
- 3.8 Tangent Line Approximation and Differentials
Chapter 4: Integration
- 4.1 Antiderivatives and Indefinite Integrals
- 4.2 Riemann Sum and Area Approximation
- 4.3 Definite Integral, Area Under a Curve, and Application
- 4.4 Properties of Definite Integral
- 4.5 Trapezoidal Rule
- 4.6 The Fundamental Theorem of Calculus Part 1
- 4.7 The Fundamental Theorem of Calculus Part 2
- 4.8 Integration by Substitution
- 4.9 Integration of Exponential and Logarithmic Function
Chapter 5: Applications of Integration
- 5.1 Area of a Region between Two Curves
- 5.2 Volumes by Disk and Washers
- 5.3 Volumes of Solids with Known Cross Sections
- 5.4 The Total Change Theorem (Application of FTC)
- 5.5 Motion of a Particle, Distance, and Displacement
- 5.6 Average Value of a Function
- 5.7 Length of a Curve (Distance Traveled Along a Curve) $\boxed{\text{BC}}$
Chapter 7: Further Applications of Integration
Chapter 8:Parametric Equations, Vectors, and Polar Coordinates $\boxed{\text{BC}}$
Chapter 9: Infinite Sequences and Series $\boxed{\text{BC}}$
- 9.1 Sequences and Series
- 9.2 The Integral Test and p–Series
- 9.3 The Comparison Test
- 9.4 Alternating Series and Error Bound
- 9.5 The Ratio Test
- 9.6 Convergence of Power Series
- 9.7 Representations of Functions as Power Series
- 9.8 Taylor Polynomial and Lagrange Error Bound
- 9.9 Taylor Series and Maclaurin Series
Course Content