3.7 Optimization Problems
When you are given a word problem that asks for the maximum or minimum value of a certain quantity, you have to translate the word problem into a mathematical equation for the quantity that is to be maximized or minimized. The differential calculus is a powerful tool for solving these kind of problems.
Guidelines for Solving Optimization Problems
1. Read the problem carefully until you understand it.
2. In most problems it is useful to draw a picture. Label it with the quantities given in the problem.
3. Assign a variable to the unknown quantity and write an equation for the quantity that is to be maximized (or minimized), since this equation will usually involve two or more variables.
4. Use the given information to find relationships between these variables. Use these equations to eliminate all but one variable in the equation.
5. Use the first and second derivatives tests to find the critical points.
Example
- Find the points on the curve $f(x)=\sqrt{x}$ that is nearest to the point $(3,0)$.
▶️Answer/Explanation
Solution
Sketch the graph of $f(x)=\sqrt{x}$.
The distance between the point $(3,0)$ and a point $(x, y)$ on the graph of $f(x)=\sqrt{x}$ is given by
$
\begin{aligned}
d & =\sqrt{(x-3)^2+(y-0)^2} \\
& =\sqrt{(x-3)^2+(\sqrt{x}-0)^2} \\
& =\sqrt{x^2-6 x+9+x} \\
& =\sqrt{x^2-5 x+9}
\end{aligned}
$
We need only find the critical numbers of $g(x)=x^2-5 x+9$, because $d$ is smallest when the expression inside the radical is smallest.
$
g^{\prime}(x)=2 x-5=0 \Rightarrow x=5 / 2
$
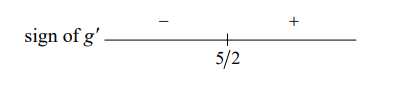
The first derivative test verifies that $x=5 / 2$ yields a relative minimum.
The point on the curve closest to $(3,0)$ is $(5 / 2, \sqrt{5 / 2})$.
Exercises – Optimization Problems
Multiple Choice Questions
1. The point on the curve $y=2-x^2$ nearest to $(3,2)$ is
(A) $(0,2)$
(B) $\left(\frac{1}{2}, \frac{7}{4}\right)$
(C) $\left(\frac{3}{4}, \frac{23}{16}\right)$
(D) $(1,1)$
▶️Answer/Explanation
Ans:D
Question
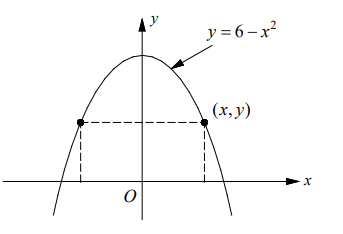
- What is the area of the largest rectangle that has its base on the $x$-axis and its other two vertices on the parabola $y=6-x^2$ ?
(A) $8 \sqrt{2}$
(B) $6 \sqrt{2}$
(C) $4 \sqrt{3}$
(D) $3 \sqrt{2}$
▶️Answer/Explanation
Ans:A
Question
- If $y=\frac{1}{\sqrt{x}}-\sqrt{x}$, what is the maximum value of the product of $x y$ ?
(A) $\frac{1}{9}$
(B) $\frac{\sqrt{3}}{9}$
(C) $\frac{2 \sqrt{3}}{9}$
(D) $\frac{2}{3}$
▶️Answer/Explanation
Ans:C
Question
- If the maximum value of the function $y=\frac{\cos x-m}{\sin x}$ is at $x=\frac{\pi}{4}$, what the value of $m$ ?
(A) $-\sqrt{2}$
(B) $\sqrt{2}$
(C) -1
(D) 1
▶️Answer/Explanation
Ans:B
