Volumes of Solids with Known Cross Sections
The volume of a solid of known cross-sectional area $A(x)$ from $x=a$ to $x=b$ is the integral of $A$ from $a$ to $b$.
1. For cross sections of area $A(x)$ taken perpendicular to the $x$-axis, the volume is
$
V=\int_a^b A(x) d x
$
2. For cross sections of area $A(y)$ taken perpendicular to the $y$-axis, the volume is
$
V=\int_c^d A(y) d y
$
Example 1
- The base of a solid is the region in the first quadrant enclosed by the graph of $y=-x^2+2 x$ and the $x$-axis. If every cross section of the solid perpendicular to the $x$-axis is an equilateral triangle, what is the volume of the solid?
▶️Answer/Explanation
Solution
Sketch the typical cross section.
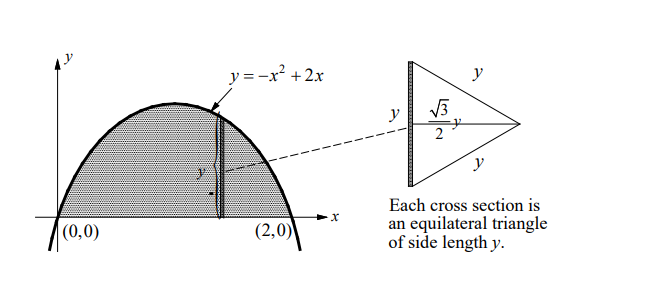
The area of each cross section is
$
\begin{aligned}
& A(x)=\frac{1}{2}(\text { base })(\text { height })=\frac{1}{2}(y)\left(\frac{\sqrt{3}}{2} y\right)=\frac{\sqrt{3}}{4} y^2 \\
& =\frac{\sqrt{3}}{4}\left(-x^2+2 x\right)^2 \\
& =\frac{\sqrt{3}}{4}\left(x^4-4 x^3+4 x^2\right) \\
&
\end{aligned}
$
The equilateral triangles lie on the plane from $x=0$ to $x=2$. The volume is
$
\begin{aligned}
V & =\int_a^b A(x) d x=\int_0^2 \frac{\sqrt{3}}{4}\left(x^4-4 x^3+4 x^2\right) d x \\
& =\frac{\sqrt{3}}{4}\left[\frac{x^5}{5}-x^4+\frac{4}{3} x^3\right]_0^2=\frac{4 \sqrt{3}}{15}
\end{aligned}
$
Example 2
- The base of a solid is the region enclosed by the graph of $y=e^x$, the coordinate axes, and the line $x=1$. If the cross sections of the solid perpendicular to the $x$-axis are squares, what is the volume of the solid?
(A) $\frac{e^2}{4}$
(B) $\frac{e^2-1}{2}$
(C) $\frac{e^2+1}{2}$
(D) $e^2-\frac{1}{2}$
▶️Answer/Explanation
Ans:B
Example 3
- The base of a solid is the region enclosed by the graph of $y=\sqrt{x}$, the $x$-axis, and the line $x=2$. If each cross section perpendicular to the $x$-axis is an equilateral triangle, what is the volume of the solid?
(A) $\frac{\sqrt{3}}{8}$
(B) $\frac{\sqrt{3}}{6}$
(C) $\frac{\sqrt{3}}{4}$
(D) $\frac{\sqrt{3}}{2}$
▶️Answer/Explanation
Ans:D
Example 4
- The base of a solid is the region in the first quadrant bounded by the coordinate axes, and the line $2 x+3 y=6$. If the cross sections of the solid perpendicular to the $x$-axis are semicircles, what is the volume of the solid?
(A) $\frac{\pi}{2}$
(B) $\frac{3 \pi}{4}$
(C) $\pi$
(D) $\frac{3 \pi}{2}$
▶️Answer/Explanation
Ans:A
Example 5
- The base of a solid $S$ is the semicircular region enclosed by the graph of $y=\sqrt{9-x^2}$ and the $x$-axis. If the cross sections of $S$ perpendicular to the $x$-axis are semicircles, what is the volume of the solid?
(A) $\frac{20 \pi}{3}$
(B) $6 \pi$
(C) $\frac{9 \pi}{2}$
(D) $\frac{7 \pi}{2}$
▶️Answer/Explanation
Ans:C
Example 6
- The base of a solid is the region bounded by the graph of $y=\sqrt{x}$, the $x$-axis and the line $x=4$. If the cross sections of the solid perpendicular to the $y$-axis are squares, the volume of the solid is given by
(A) $\int_0^2\left(4-y^2\right)^2 d y$
(B) $\int_0^2(4-y)^2 d y$
(C) $\int_0^2\left[(2-y)^2\right]^2 d y$
(D) $\int_0^4\left[(2-y)^2\right]^2 d y$
▶️Answer/Explanation
Ans:A
