The Product Rule
If f and g are both differentiable, then \(\frac{d}{dx}\left [ f\left ( x \right ) g\left ( x \right )\right ]=f\left ( x \right ){g}’\left ( x \right )+g\left ( x \right ){f}’\left ( x \right ).\)
The Quotient Rule
If f and g are both differentiable, then \(\frac{d}{dx}\left [ \frac{f\left ( x \right )}{g\left ( x \right )} \right ]=\frac{g\left ( x \right ){f}’\left ( x \right )-f\left ( x \right ){g}’\left ( x \right )}{\left [ g\left ( x \right ) \right ]^{2}}.\)
Higher Derivatives
If f is a differentiable function, then its derivative f ′ is also a function, so f ′ may have a derivative of its own. The second derivative f ′′ is the derivative of f ′ and the third derivative f ′′′ is the derivative of the second derivative.
In general, the nth derivative of f is denoted by f(n) f and is obtained from f by differentiating n times. Higher derivatives are denoted as follows.

Example 1
- Differentiate the function \(f\left ( x \right )=\left ( x^{3}-7 \right )\left ( x^{2}-4x \right ).\)
▶️Answer/Explanation
Solution
\({f}’\left ( x \right )=\left ( x^{3}-7 \right )\frac{d}{dx}\left ( x^{2}-4x \right )+\left ( x^{2}-4x \right )\frac{d}{dx}\left ( x^{3} -7\right )\) The product rule
\(=\left ( x^{3}-7 \right )\left ( 2x-4 \right )+\left ( x^{2}-4x \right )\left ( 3x^{2} \right )\)
\(=5x^{4}-16x^{3}-14x+28\)
Example 2
- Differentiate the function \(f\left ( x \right )=\frac{3x^{2}-x}{\sqrt{x+1}}.\)
▶️Answer/Explanation
Solution
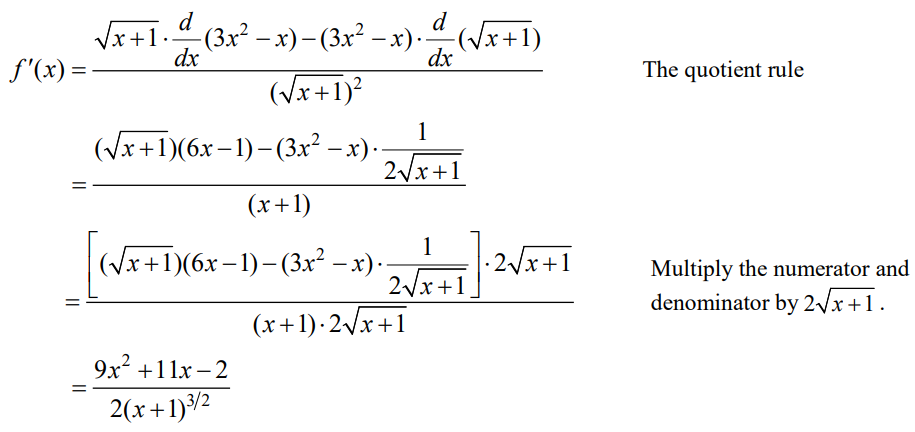
Example 3
- If \(f\left ( x \right )=\frac{1}{6}x^{3}+24\sqrt{x},\) find \({f}’\left ( x \right ),{f}”\left ( x \right ),{f}”’\left ( x \right ),{f}”’\left ( 9 \right ).\)
▶️Answer/Explanation
Solution
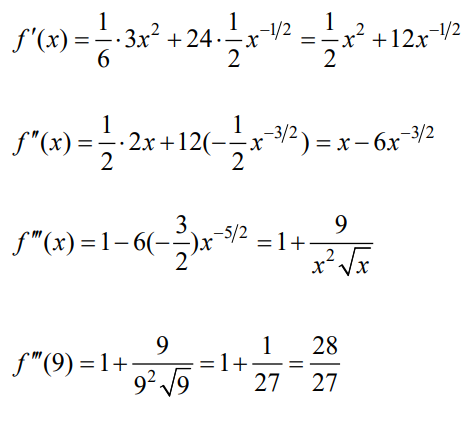
Exercises – The Product and Quotient Rules and Higher Derivatives
Multiple Choice Questions
- If \(f\left ( x \right )=\left ( x^{3}-2x+5 \right )\left ( x^{-2}+x^{-1} \right ),\) then \({f}’\left ( 1 \right )=\)
(A) −10 (B) -6 (C) \(-\frac{9}{2}\) (D) \(\frac{7}{2}\)
▶️Answer/Explanation
Ans:
1. A
- If \(f\left ( x \right )=\frac{\sqrt{x}-1}{^{\sqrt{x}+1}}\) then \({f}’\left ( x \right )=\)
(A) \(\frac{\sqrt{x}}{\left ( \sqrt{x}+1 \right )^{2}}\)
(B) \(\frac{x}{\left ( \sqrt{x}+1 \right )^{2}}\)
(C) \(\frac{1}{\sqrt{x}\left ( \sqrt{x} +1\right )^{2}}\)
(D) \(\frac{\sqrt{x}-1}{\sqrt{x}\left ( \sqrt{x}+1 \right )^{2}}\)
▶️Answer/Explanation
Ans:
2. C
- 3. If \(g\left ( 2 \right )=3\) and \({g}’\left ( 2 \right )=-1\), what is the value of \(\frac{d}{dx}\left ( \frac{g\left ( x \right )}{x^{2}} \right )\) at x=2?
(A) -3 (B) -1 (C) 0 (D) 2
▶️Answer/Explanation
Ans:
3. B
4. If \(f\left ( x \right )=\frac{x}{x-\frac{a}{x}}\) and \({f}’\left ( 1 \right )=\frac{1}{2}\), what is the value of a ?
(A) \(-\frac{5}{2}\) (B) -1 (C) \(\frac{1}{2}\) (D) 2
▶️Answer/Explanation
Ans:
4. B
5. If \(y=4\sqrt{x}-16\sqrt[4]{x}\), then \({y}”=\)
(A) \(\sqrt[4]{x}-3\) (B) \(-3\sqrt{x}+3\) (C) \(\frac{-\sqrt[4]{x}+3}{x\sqrt[4]{x^{3}}}\) (D) \(\frac{\sqrt{x}-3}{x\sqrt[4]{x}}\)
▶️Answer/Explanation
Ans:
5. C
5. If \(y=4\sqrt{x}-16\sqrt[4]{x}\), then \({y}”=\)
(A) \(\sqrt[4]{x}-3\) (B) \(-3\sqrt{x}+3\) (C) \(\frac{-\sqrt[4]{x}+3}{x\sqrt[4]{x^{3}}}\) (D) \(\frac{\sqrt{x}-3}{x\sqrt[4]{x}}\)
▶️Answer/Explanation
Ans:
5. C
6. If \(y=x^{2}\cdot f\left ( x \right )\), then \({y}”=\)
(A) \(x^{2}{f}”\left ( x \right )+x{f}’\left ( x \right )+2f\left ( x \right )\)
(B) \(x^{2}{f}”\left ( x \right )+x{f}’\left ( x \right )+f\left ( x \right )\)
(C) \(x^{2}{f}”\left ( x \right )+2x{f}’\left ( x \right )+f\left ( x \right )\)
(D) \(x^{2}{f}”\left ( x \right )+4x{f}’\left ( x \right )+2f\left ( x \right )\)
▶️Answer/Explanation
Ans:
6. D
7. Let \(f\left ( x \right )=\frac{1}{2}x^{6}-10x^{3}+12x\). What is the value of \(f\left ( x \right )\), when \({f}”\left ( x \right )=0?\)
(A) \(-\frac{23}{4}\) (B) \(-\frac{3}{2}\) (C) \(\frac{1}{2}\) (D) \(\frac{5}{2}\)
▶️Answer/Explanation
Ans:
7. D
Free Response Questions
8. Let \(h\left ( x \right )=x\cdot f\left ( x \right )\cdot g\left ( x \right )\). Find \({h}’\left ( 1 \right )=-2,g\left ( 1 \right )=3,{f}’\left ( 1 \right )=1,\) and \({g}’\left ( 1 \right )=\frac{1}{2}.\)
▶️Answer/Explanation
Ans:
8. −4
9. Let \(g\left ( x \right )=\frac{x}{\sqrt{x}-1}\). Find \({g}”\left ( 4 \right ).\)
▶️Answer/Explanation
Ans:
9. 1/8
